无压差下刷式密封刷丝的力学特性分析
张浩,康宇驰,顾文娟,张家豪,许嘉辉
(650093 云南省 昆明市 昆明理工大学 机电工程学院)
0 引言
刷式密封是具有优良密封性能的接触式动密封,是航空发动机等旋转机械的关键部件。近年来,随着航空发动机技术要求的提高,航空发动机压力、转速等慢慢向高参数方向发展。刷丝的形变会造成泄露损失[1]、滞后效应[2]、刷丝疲劳断裂[3],直接影响到刷式密封的密封性和使用寿命,所以对于刷丝的形变研究有着重大的意义。
国内外学者对于刷丝的形变进行了大量的研究。Modi[4]采用材料力学中的悬臂梁模型,提出单根刷丝自由端与转子面接触力的计算方法;黄首清等[5]基于力矩平衡和线性叠加原理,提出气流力引起刷丝尖端力、转矩的定量计算方法;孙丹等[6]在前人的基础上延用悬臂梁理论建立了刷丝的力学理论模型,计算了刷丝在气流力作用下的变形。
现有研究对于刷丝的力学分析多基于材料力学中悬臂梁的微小变形理论,对于大变形的研究相对较少。刷丝实际工作中自由端会产生很大的挠度,这种挠度称为刷丝的大变形。对于大变形的研究多数是以悬臂梁为结构件,大多数的情况是对于尖端载荷下的情况进行研究分析。Bishop 等[7]提供了在尖端垂直载荷下的悬臂梁的几何非线性大变形的经典数学解决方案;Wang[8]提出了分别用于梁的尖端和均匀分布载荷下的非线性弯曲的数值方法。
基于大变形理论对无压差下刷丝形变进行研究,本文将刷丝与转子接触发生的形变类似看做斜弯曲。在已发表的刷式密封力学特性研究模型中,一个共同的特点是刷丝的形变分析是在2 个正交平面单独进行的,并且最后采用迭加原理进行求解。
本文是对无压差下的刷式密封的刷丝进行力学特性研究。首先对无压差下的刷丝进行受力分析,分别采用材料力学中的线性梁非线性梁理论(大小变形理论)对刷丝的形变进行求解;然后使用ABAQUS 软件建立无压差下的刷式密封迟滞特性模型,与前人实验数据进行对比验证数值模型的正确性。建立不同参数的刷式密封结构,对不同情况下的数值模型与解析解的结果进行对比分析。本文的研究对揭示在无压差工作下的刷丝运动具有一定意义,为提高刷式密封泄漏率以及使用寿命,改善刷式密封结构提供了理论依据。
1 刷丝形变的理论模型
图1 为刷丝在转子作用下(XOZ)的受力分析。由于刷丝在径向尺寸远小于轴向尺寸,因此将刷丝简化为梁问题进行处理。刷丝在 A 点由焊接等方法固定,B 端为自由端,因此将刷丝视为悬臂梁。本文所研究的形变均为梁中性轴的形变,忽略半径对形变的影响,这也是材料力学中计算悬臂梁弯曲问题的常用方法。

图1 刷丝受力分析图(XOZ)平面Fig.1 Bristle force analysis diagram (XOZ) plane
图1 中刷丝的长度为L,原点坐标位于刷丝固定端A 点,沿着刷丝的轴向方向为X 轴,沿着刷丝的径向方向为Z 轴。AB 是刷丝在初始时位置的形貌,JQ 是初始位置时的转子。AB'是与转子发生接触后发生形变的刷丝面貌,为平面内的一条曲线,称为挠曲线,挠曲线上X 的任意点的纵坐标用yd表示称为挠度。J'Q'是当转子发生偏心运动到最高点的位置,δP是转子偏心运动的位移,θ1是刷丝的倾角。FB是刷丝在自由端受到转子的接触力,FBx和FBz是FB在X 方向和Z 方向的投影分量。
材料力学中挠曲线的近似微分方程为

对式(1)进行积分,可得刷丝小变形自由端的挠度:

通过三角函数关系可得FB与δp之间的关系:

对于小变形运用挠曲线的近似微分方程对刷丝形变进行求解,得到刷丝的挠度方程为

对式(5)进行求解,得通解为

对式(6)求1 阶微分可得:

式(7)中,D11和D12为未知常数,这2 个未知常数可以通过边界条件求解。


式(8)中,FBz=FBsinθ1,FBx=FBcosθ1,从而可以求出D11,D12。
将求解结果代入式(6)可以得到刷丝形变。
在材料力学中,计算悬臂梁的大变形采用精确解:

对式(9)进行数学求解可以得:

式(10)为刷丝在径向载荷FBz下发生形变的挠度。
对于刷丝在轴向FBx下发生的形变进行求解分析。假设刷丝是理想直线,当轴向载荷FBx小于刷丝临界载荷时,刷丝是稳定的;当轴向载荷FBx大于刷丝临界载荷时,刷丝失稳。对刷丝在轴向载荷FBx下的临界载荷进行分析求解。
压杆稳定的临界压力的欧拉公式[9]:

其中μ为压杆的长度因数,刷丝的约束条件是一端固定、另一端为铰支(自由端为固定端,与转子接触的自由端类似于铰支),μ≈0.7,得

对于刷丝,在转子的作用下对其径向产生的干扰力FBx存在2 种情况,第1 种是刷丝稳定:

第2 种为刷丝失稳:

结合刷丝实际工况,分析第2 种刷丝大变形的情况。刷丝在径向载荷FBx作用下发生的大变形为

因为在大挠度的情况下,刷丝尖端力无法准确用数学算式表达出来,这里采用形变的微小形变公式进行基本的判断。将FBx=FBcosθ1,以及式(3)、式(12)代入式(15)可得:

已知θ1是刷丝的倾角,此处π ≈3.14,所以
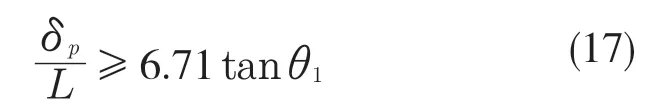
综上,在实际工况中只存在第1 种情况,在径向载荷FBx的作用下刷丝在径向产生微小变形。
图2 所示为刷丝在径向载荷FBx的受力分析,图2 中:L 为刷丝长度,yx为刷丝在径向载荷FBx下的挠度。

图2 刷丝径向载荷FBx 下的受力分析Fig.2 Bristle force analysis diagram under radial load FBx
若只取压力FBx的绝对值,则当yx为正时,M 为负;yx为负时,M为正。即M 与yx的正负号相反,所以

将式(18)代入式(1)可得:
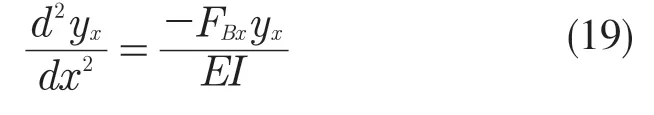

式(21)中A,B 为积分常数。刷丝在此时的边界条件为

代入边界条件,求解式(21)可得:


式(24)中的A 为刷丝在径向载荷下的中点坐标,可以通过数值模型进行确认。在径向载荷FBx作用下的挠度为yx,刷丝在自由端在转子的作用力下总挠度yd为

即刷丝在FB作用下挠度的解析解为

2 数值模型准确性验证
本文使用Demiroglu 等[10]的实验结果验证数值模型的准确性,图3 是实验示意图。用一个载荷块代替转子,载荷块的上下运动代替转子的偏心运动,转子的转动并未在实验中考虑。

图3 实验测量刷丝束转子接触力示意图Fig.3 Schematic diagram of experimental measurement of contact force between bristle pack and rotor


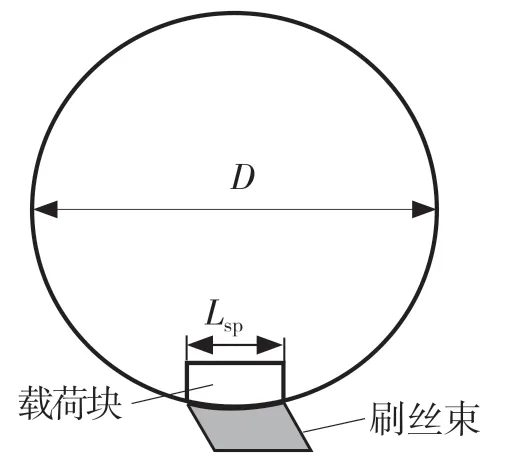
图4 刷丝与载荷块示意图Fig.4 Schematic diagram of contact between bristle pack and load block
本文采用如图5 所示的几何模型,该模型包含1 个背板,1 个转子和22 根刷丝。模型需要确定的几何参数如表1 所示。22 根刷丝分布成3 排,刷丝以叉排形式排列。该模型单元选取与边界条件参考了Duran[11]等人提出的模型。

图5 ABAQUS 几何模型图Fig.5 ABAQUS numerical model geometry schematic

表1 刷式密封模型主要几何参数Tab.1 Main parameters of brush seal model
模型采用三维实体单元C3D8R。刷丝在转子的接触力作用发生了弯曲,可以将刷丝看作为Euler-Bernoulli 梁,本文采用B31 单元构建刷丝。对于边界条件的选取也与Duran 等的研究保持一致。模型中对接触的设置采用General contact 方式定义。模型中刷丝之间接触用梁-梁接触方式(edge-to-edge contact)构建,刷丝与背板之间的接触由梁-面接触方式构建,刷丝与转子之间的接触由点-面接触方式构建。刷丝固定端受到全约束,模仿实际工况中刷丝束在固定端焊接在一起。将背板看做为刚体,并取用一个参考点,由于背板在运动过程中保持静止,那么此参考点受到全约束。实际工况中的转子偏心运动由载荷块的上下运动实现。为了方便比较,刷丝采用haynes25 合金材料,密度为9 130 kg/m3,弹性模量213.7 GPa,泊松比为0.29。背板和转子均为刚体材料。
图6 对比了数值计算单根刷丝接触力结果和实验测量的单根刷丝接触力的结果。从图6 可以发现,在转子的上升阶段,数值模拟结果和实验结果存在一定的差异,并且随着转子位移量的增加,差距逐渐增加。在转子的上移阶段不确定的摩擦系数是导致这种差距的原因之一。除此之外,实际工况相关的设计参数不能确定,这也造成了数字结果和实验结果的差距。转子下降阶段,可以看出误差比较大,这是因为在静态数值计算中,有限元软件将分析步分解成单独的子步骤,忽略了惯性对数值模拟结果的影响。陈春行等人的数值模拟结果与该实验结果也存在类似的差距。转子上移阶段,数值结果与实验结果差距较小,足以说明数值模型的准确性。

图6 数值模拟单根刷丝接触力和实验单根刷丝接触力[12]对比Fig.6 Comparison of numerical simulation of single bristle contact force and experimental single bristle contact force[12]
3 数值模拟结果与解析式对比分析
为研究解析解的准确性,本文通过建立不同的数值模型进行对比分析,几何参数如表2 所示。按照几何分类,可以将几何模型分成3 类。几何模型1、2 有相同的刷丝倾角θ和刷丝直径d,不同的刷丝长度L;几何模型3、4 有相同的刷丝长度L 和刷丝直径d,不同的刷丝倾角θ;几何模型5、6 用相同的刷丝长度L和刷丝倾角θ,不同的刷丝直径d。

表2 ABAQUS 数值模型几何参数Tab.2 Geometry parameters of ABAQUS numerical models
几何模型1 中,刷丝的长度L=12 mm,直径d=0.13 mm,刷丝倾角θ1=45°。图7 对比了此模型下的小变形公式(6)以及大变形公式(26)的计算结果与数值模拟结果。图7 可以明显发现,刷丝从固定端到6.8 mm 位置,小变形公式(6)的求解结果与数值模拟结果呈高度一致性。从6.8 mm 到自由端,小变形公式(6)计算结果与数值模拟结果误差较大,大变形公式(26)计算结果与数值模拟结果呈高度一致性。

图7 模型1 L=12 mm,d=0.13 mm,θ1=45°Fig.7 Model 1 L=12 mm,d=0.13 mm and θ1=45°
模型2,刷丝长度L=13 mm,直径d=0.13 mm,刷丝倾角θ1=45°。图8 对比了式(6)及式(26)计算结果与数值模拟结果。由图8 可见,刷丝从固定端到7.6 mm 位置,式(6)求解结果与数值模拟结果呈高度一致性。从7.6 mm 到自由端,式(6)计算结果与数值模拟结果误差较大,式(26)计算结果与数值模拟结果呈高度一致性。

图8 模型2 L=13 mm,d=0.13 mm,θ1=45°Fig.8 Model 2 L=13 mm,d=0.13 mm and θ1=45°
模型3,刷丝长度L=12.5 mm,直径d=0.13 mm,刷丝倾角θ1=35°。图9 对比了式(6)及式(26)计算结果与数值模拟结果。由图9 可见,刷丝从固定端到7.226 56 mm 位置,式(6)的求解结果与数值模拟结果呈高度一致性。从7.226 56 mm 到自由端式(6)计算结果与数值模拟结果误差较大,式(26)计算结果与数值模拟结果呈高度一致性。

图9 模型2 L=12.5 mm,d=0.13 mm,θ1=35°Fig.9 Model 2 L=12.5 mm,d=0.13 mm and θ1=35°
模型4,刷丝长度L=12.5 mm,直径d=0.13 mm,刷丝倾角θ1=40°。图10 对比了式(6)及式(26)计算结果与数值模拟结果。由图10 可见,刷丝从固定端到7.226 56 mm 位置,式(6)的求解结果与数值模拟结果呈高度一致性。从7.226 56 mm 到自由端,式(6)计算结果与数值模拟结果误差较大,式(26)计算结果与是数值模拟结果呈高度一致性。

图10 模型4 L=12.5 mm,d=0.13 mm,θ1=40°Fig.10 Model 4 L=12.5 mm,d=0.13 mm and θ1=40°
模型5,刷丝长度L=12.5 mm,直径d=0.136 mm,刷丝倾角θ1=45°。图11 对比了式(6)及式(26)计算结果与数值模拟结果。由图11 可见,刷丝从固定端到7.226 56 mm 位置,式(6)的求解结果与数值模拟结果呈高度一致性。从7.226 56 mm 到自由端,式(6)计算结果与数值模拟结果误差较大,式(26)计算结果与数值模拟结果呈高度一致性。

图11 模型5 L=12.5 mm,d=0.136 mm,θ1=45°Fig.11 Model 5 L=12.5 mm,d=0.136 mm and θ1=45°
模型6,刷丝长度L=12.5 mm,直径d=0.142 mm,刷丝倾角θ1=45°。图12 对比了式(6)及式(26)计算结果与数值模拟结果。由图12 可见,刷丝从固定端到7.226 56 mm 位置,式(6)的求解结果与数值模拟结果呈高度一致性。从7.226 56 mm 到自由端,式(6)计算结果与数值模拟结果误差较大,式(26)计算结果与数值模拟结果呈高度一致性。
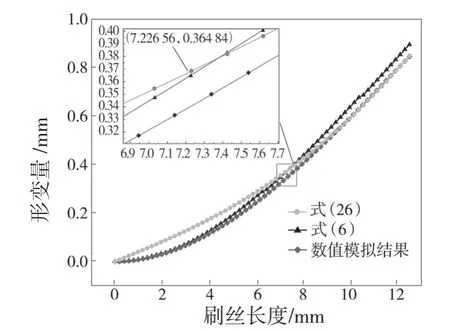
图12 模型6 L=12.5 mm,d=0.142 mm,θ1=45°Fig.12 Model 6 L=12.5 mm,d=0.142 mm and θ1=45°
4 总结
本文研究了无压差下刷式密封刷丝的力学特性。对无压差工作下的刷式密封的刷丝与转子接触作用下的受力情况进行力学分析,并采用用材料力学中的线性和非线性梁理论进行求解。采用商用软件ABAQUS 构建3 排22 根刷丝模型,通过构建不同的几何模型分析比较数学模型与数值模型的计算结果。主要结论如下:
(1)本文所构建的无压差下的3 排22 根刷式密封结构中单根刷毛的数值模拟结果与前人实验结果误差不大,验证了数值模型的正确性。
(2)采用材料力学中的悬臂梁理论以及数学方法,求解出轴向载荷下的刷丝挠度方程。结合刷丝实际工况,对刷丝轴向载荷进行对比分析。刷丝的轴向载荷不得超过刷丝的受力极限。因此刷丝在轴向载荷作用下的变形为微小变形。
(3)对比分析6 组几何模型下的式(6)、式(26)以及ABAQUS 数值模拟结果。从固定端到58%位置,线性理论公式(6)求解结果与ABAQUS 数值模拟结果高度一致,非线性理论公式(26)从58%位置到自由端与ABAQUS数值模拟结果高度一致。

