Lupa q-Bézier曲线的离散卷积生成与求值算法*
耿梦圆,解 滨,韩力文,3,4
(1.河北师范大学数学科学学院,河北 石家庄 050024;2.河北师范大学计算机与网络空间安全学院,河北 石家庄 050024;3.河北省计算数学与应用重点实验室,河北 石家庄 050024;4.河北省数学与交叉科学国际联合研究中心,河北 石家庄 050024)
1 引言
在计算机辅助几何设计CAGD(Computer Aided Geometric Design)中,Bernstein基函数因其优良性质使得Bézier曲线曲面成为描述自由曲线曲面的重要工具[1-3]。 近年来,q-微积分理论[4]引发众多研究人员的研究兴趣并在超几何分析、量子力学等领域广为应用。 其迅猛发展促使基于q-整数的广义Bernstein算子陆续被提出,其中研究较为广泛的主要为Lupaq-Bernstein算子和Phillipsq-Bernstein算子。 1987年,Lupa[5]首次提出有理形式的q-模拟Bernstein算子,研究其逼近和保形性质,后被称之为Lupaq-Bernstein算子。 Ostrovska[6]和Wang等[7]探究了算子的一致收敛性及收敛速度等问题。 1996年Phillips[8]引入基于q-整数的多项式形式的q-Bernstein算子,可由q-差分简单表示,为便于区分,本文称之为Phillipsq-Bernstein算子。 随后Oruç等[9]构造出Phillipsq-Bézier曲线,引起研究人员的关注与研究。 在此带动与影响下,带有形状参数的广义Bézier曲线曲面在曲线曲面造型上发挥了重要作用。
2014年,Han等[10]依据Lupaq-Bernstein算子构造出基于q-整数的Lupaq-Bézier曲线曲面,得到了曲线的几何不变性、升阶等性质及de Casteljau算法等。 相比于Phillipsq-Bézier曲线,Lupaq-Bézier曲线的函数类型、形状参数q的取值范围及端点相切的性质均不同:(1) Phillipsq-Bézier曲线为多项式形式且参数q∈(0,1],而Lupaq-Bézier曲线为有理函数形式且q∈(0,+∞),取值范围更广;(2) Phillipsq-Bézier曲线仅与首控制边相切,而Lupaq-Bézier曲线与首末控制边均相切。
2 预备知识
2.1 Lupa q-Bézier曲线的相关定义
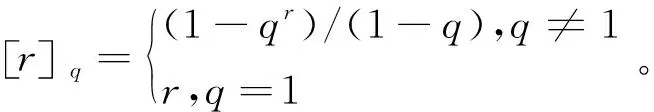
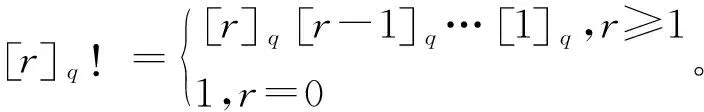
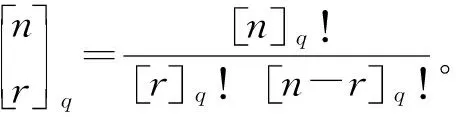
特别地,q-二项式系数满足Pscal-type关系式,如式(1)和式(2)所示:
(1)
(2)
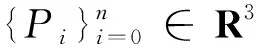
(3)
为n次Lupaq-Bézier曲线,其中:
(4)
为n次Lupaq-Bernstein基函数。 当q=1时,Lupaq-Bézier曲线退化为经典Bézier曲线。
2.2 离散卷积的相关定义
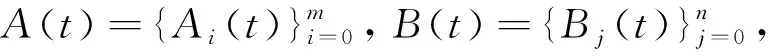
(5)
离散卷积满足交换律及结合律,如式(6)和式(7)所示:
A(t)⊗B(t)=B(t)⊗A(t)
(6)
A(t)⊗(B(t)⊗C(t))=(A(t)⊗B(t))⊗C(t)
(7)
定义6[20]离散卷积的微分法则,如式(8)所示:
(A(t)⊗B(t))′=
A′(t)⊗B(t)+A(t)⊗B′(t)
(8)
3 离散卷积生成Lupa q-Bézier曲线
3.1 Lupa q-Bernstein基函数的离散卷积形式
根据q-二项式系数满足的Pascal-type关系式(1),给出Lupaq-Bernstein基函数的递推关系。
引理1[10]n次Lupaq-Bernstein基函数是2个n-1次Lupaq-Bernstein基函数的仿射组合,如式(9)所示:
(9)
利用此递推关系式,从零次基函数开始,依次向高一次的基函数递推,得到Lupaq-Bernstein基函数的向下递推三角形,如图1所示。 从上至下第i层的中间节点恰好是第i次的Lupaq- Bernstein基函数。

Figure 1 Downward recurrence of Lupa q-Bernstein basis functions图1 Lupa q-Bernstein基函数的向下递推
n次Lupaq-Bernstein基函数出现在第n层向下递推三角形的底部。 同时,基函数是由顶端到底部第i个位置的所有路径乘积之和,例如,对于4次Lupaq-Bernstein基函数式(10)成立:
(10)
结合定义5,此过程等同于函数序列离散卷积的计算过程,由此构造出Lupaq-Bernstein基函数的离散卷积形式。
定理1设函数序列如式(11)所示:
k=1,2,…n
(11)
则Ak(t;q)可离散卷积生成n次Lupaq- Bernstein基函数序列,如式(12)所示:
A1(t;q)⊗…⊗Ak(t;q)⊗…⊗An(t;q)
(12)
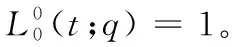
注1当q=1时,式(12)退化为经典Bernstein基函数的离散卷积形式[20]。
注2文献[15]主要围绕Lupaq-Bernstein基函数的离散概率模型给出离散卷积形式。本文则是从基函数的向下递推结合路径角度得到该形式,同时在下文中将进一步发挥离散卷积表示与向下递推三角形的作用,探究Lupaq-Bézier曲线的特点与优良性质。
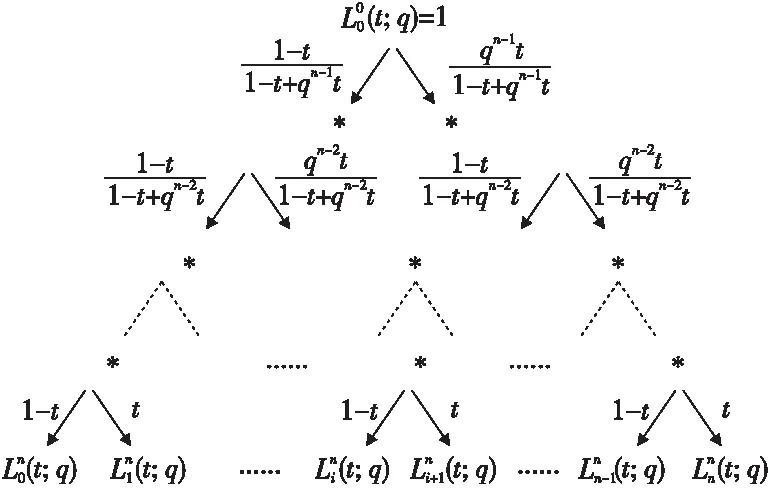
Figure 2 Basis functions constructed by convolutionof function sequences in reverse order图2 函数序列逆序卷积构造的基函数
3.2 Lupa q-Bézier曲线的de Casteljau算法
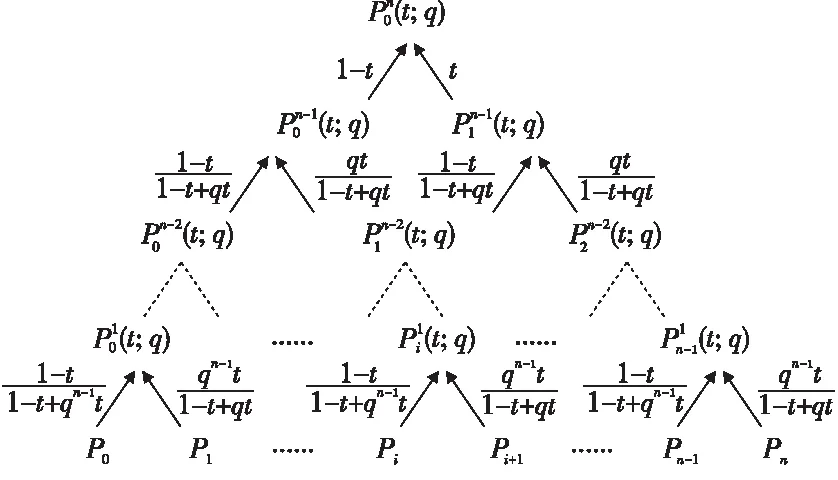
Figure 3 A de Casteljau algorithm for Lupa q-Bézier curve图3 Lupa q-Bézier曲线的一种de Casteljau算法
定理2对于任一条n次Lupaq-Bézier曲线,基于离散卷积可生成n!种de Casteljau算法。
(13)
如图4所示,当以图2定义的离散卷积顺序构造时,de Casteljau算法具有显式矩阵表示[12],记为de Casteljau算法2,如式(14)所示:
(14)
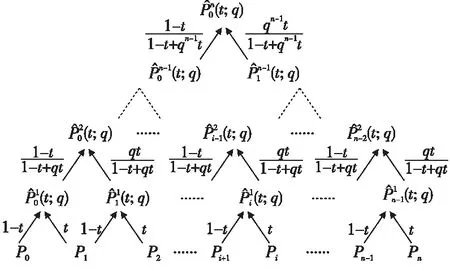
Figure 4 de Casteljau algorithm with explicit matrix representation图4 具有显式矩阵表示的de Casteljau算法
注3定理2所提出的n!种de Casteljau算法在计算Lupaq-Bézier曲线上任意点的效率上是一致的,针对不同的使用需求可选择不同的算法。
例1对于一条形状参数q=4的3次Lupaq-Bézier曲线,可生成3!种de Casteljau算法,如图5所示,‘o’点为不同算法求得的曲线上的同一点。
与经典Bézier曲线de Casteljau算法求得切点[21]不同,Lupaq-Bézier曲线de Casteljau算法倒数第2层2节点构成的直线段与曲线相交于2个点,本文将这2个交点统称为割点。 如图5所示,不同的de Casteljau算法得到的割点不同,有时为左割点,有时为右割点。 第5节将给出2种de Casteljau算法,分别求得左/右割点的判定条件。
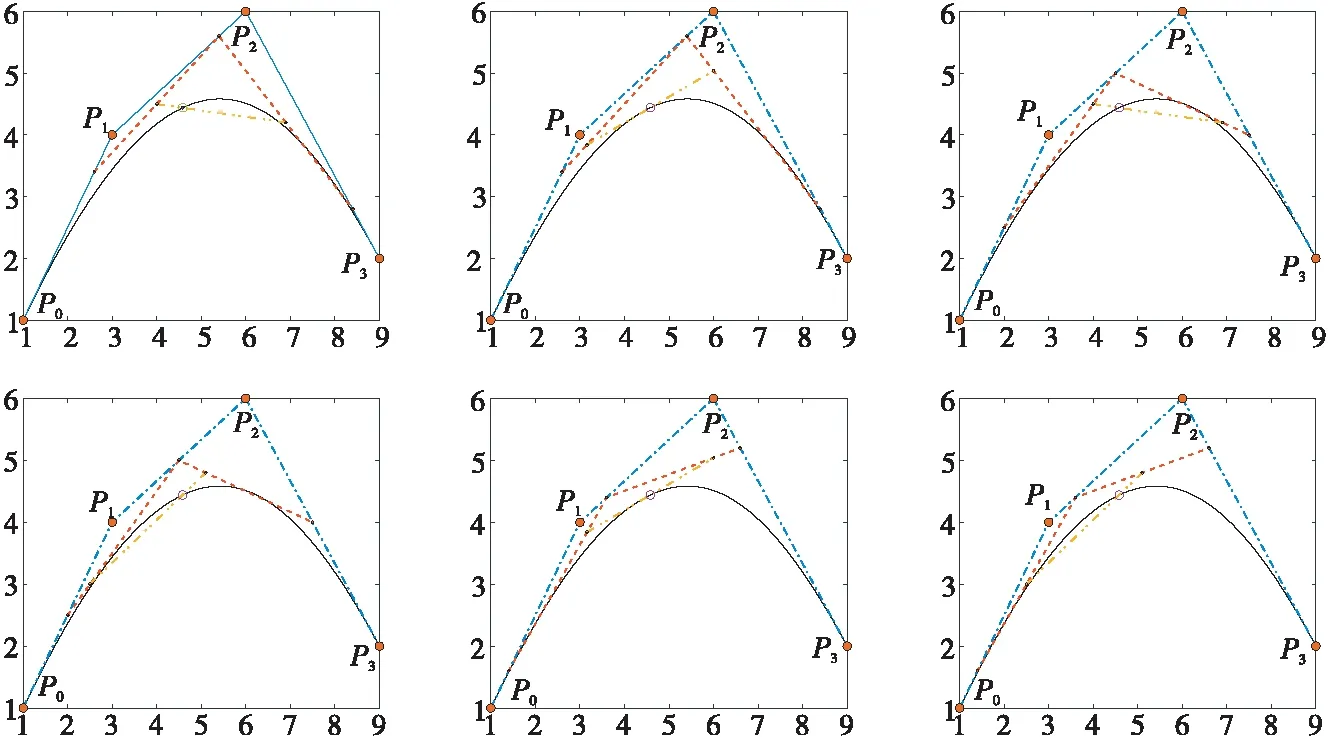
Figure 5 3! de Casteljau algorithms for cubic Lupa q-Bézier curve图5 3次Lupa q-Bézier曲线的3!种de Casteljau算法
4 速端曲线
定理3设n次Lupaq-Bézier曲线的一阶速端曲线表达式如式(15)所示:
(15)
Aj-1(t;q)⊗Bj(t;q)⊗Aj+1(t;q)⊗…⊗An(t;q)
(16)
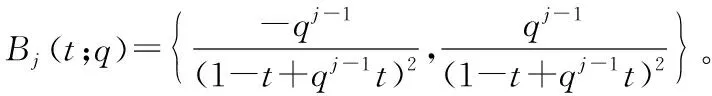
(17)
(18)
当q=1时,该速端曲线是以原曲线控制顶点的向前差分ΔP0和ΔP1为首末控制顶点的一次Bézier曲线;当q∈(0,1)∪(1,+∞)时,二次Lupaq-Bézier曲线的速端曲线是以P′(0;q),P′(1;q)为首末端点的直线段。
除此之外,通过定理3进一步整理可得到首末2个n次Lupasq-Bernstein基函数的导函数的显式表达式。
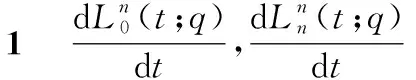
(19)
(20)
根据离散卷积的微分法则可在基函数一阶导序列式(16)的基础上继续微分,得到基函数的高阶导数,进而计算Lupaq-Bézier曲线的高阶导矢。
定理4Lupaq-Bernstein基函数的二阶导函数序列的离散卷积结构如式(21)所示:
(21)
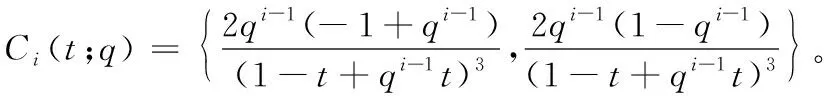
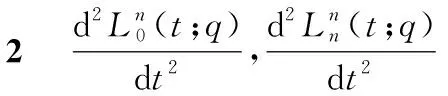
(22)
(23)
5 de Casteljau算法左/右割点分类
图3与图4为曲线具有的2种de Casteljau算法。 图6a和图6b分别展示了不同形状参数q下的二次Lupaq-Bézier曲线,其中q=1所表示的曲线为经典Bézier曲线。 由图6可知,Lupaq-Bézier曲线始终位于控制多边形与经典Bézier曲线之间,并且通过选取不同的形状参数q值,可以任意调整曲线形状,增加曲线造型的灵活性[10]。
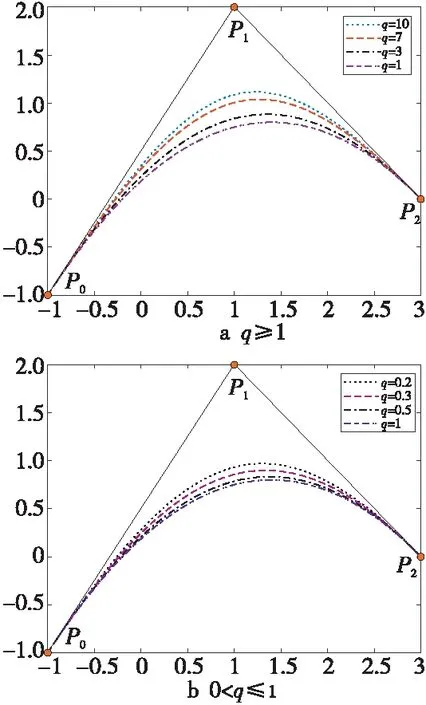
Figure 6 Quadratic Lupa q-Bézier curves with different shape parameters图6 不同形状参数的二次Lupa q-Bézier曲线
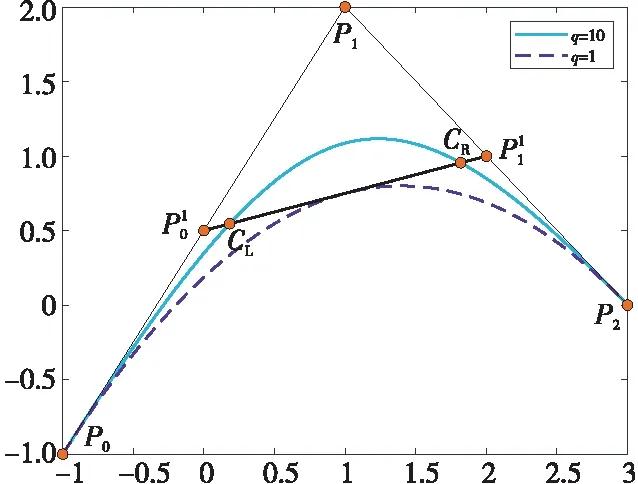
Figure 7 Comparison of de Casteljau algorithmsbetween Lupa q-Bézier curve and classical Bézier curve图7 Lupa q-Bézier曲线与经典Bézier曲线de Casteljau算法对比
下面分别给出de Casteljau算法1和算法2得到左割点或右割点时的充分必要条件。
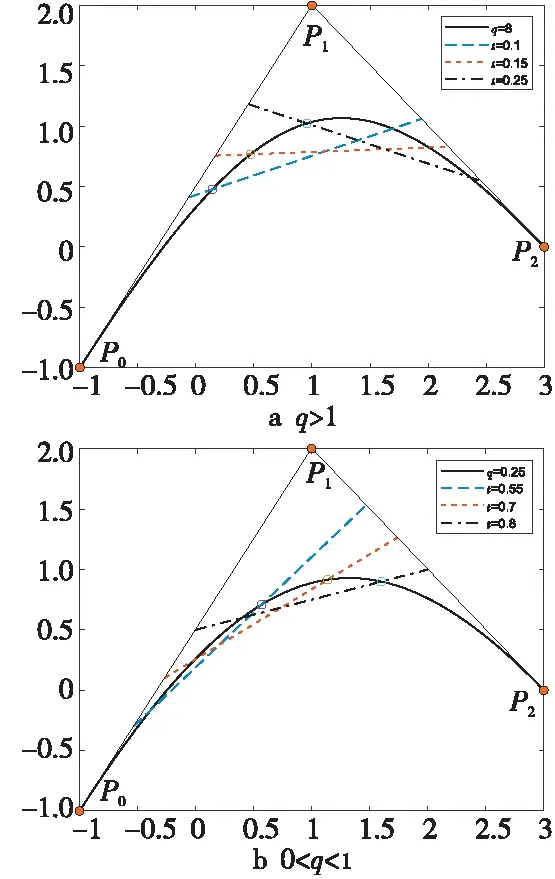
定理5任意给定参数t∈(0,1),de Casteljau算法1求得左割点当且仅当形状参数q>1;求得右割点当且仅当0 证明对比Lupaq-Bézier曲线de Casteljau算法1与经典Bézier曲线de Casteljau算法,为便于区分,记二次经典Bézier曲线de Casteljau算法节点为和 (24) (25) 定理6任意给定参数t∈(0,1),de Casteljau算法2求得左割点当且仅当形状参数0 (26) (27) 注4Lupaq-Bézier曲线具有端点插值性,即当参数t=0时,de Casteljau算法1或算法2求得参数对应曲线上一点为P0;t=1时,算法1或算法2求得曲线上一点为P2。 图8a和图8b展示了de Casteljau算法1分别在q>1时取不同参数t得到的左割点和0 Figure 8 Left/right cut points gotten by de Casteljau algorithm 1 图8 de Casteljau算法1得到的左/右割点 Figure 9 Left/right cut points gotten by de Casteljau algorithm 2 图9 de Casteljau算法2得到的左/右割点 上述定理5和定理6分别给出了de Casteljau算法1和算法2得到左割点或右割点时形状参数 的取值范围。 算法3双割点算法 输入:控制顶点P0,P1,P2,参数t,q。 输出:左/右割点CL,CR。 步骤3计算另一割点 步骤4根据形状参数的取值范围判断,倘若q≥1,则CL=C1,CR=C2;若0 定理7给定二次Lupaq-Bézier曲线P(t;q),其中q∈(0,+∞),t∈(0,1),应用双割点算法3时,节点与左/右割点CL,CR构成的交比固定。 证明当q>1时,利用双割点算法3中的步骤2与步骤3得到2个割点且CL=C1,CR=C2,则式(28)和式(29)满足: (28) 0 (29) 证毕。 本文通过引入向下递推三角形和离散卷积函数序列,提出n次Lupaq-Bernstein基函数的离散卷积结构,并将向下递推三角形反转箭头方向自下而上卷积生成Lupaq-Bézier曲线。 借助离散卷积的交换性,进而得到n!种新的de Casteljau算法。 文中列举出了其中的2种算法及其优势,对于其他算法的特征有待进一步探究。 根据对2种de Casteljau算法及其形状参数q的讨论,二次Lupaq-Bézier曲线可选择性得到左/右割点。 另外给出同时计算2个割点的算法,并证明双割点算法具有交比不变性。 本文仅得到2个n次基函数导数的显式表达式。 对于其他基函数导数的具体形式还有待探究。 对于3次或更高次Lupaq-Bézier曲线的割点讨论及其应用需要进一步研究。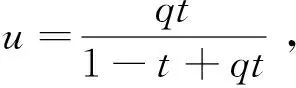


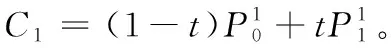
6 结束语

