融合超声波信息的机器人室内定位方法研究
李 阳,吴明晖,陈远浩
(上海工程技术大学 机械与汽车工程学院,上海 201620)
0 引言
近年来,随着无人驾驶、人工智能等技术的发展,移动机器人越来越受到人们的关注。移动机器人技术由诸多技术构成,其中定位技术最重要、最根本。准确可靠的定位与测姿是移动机器人完成任务的先决条件[1]。
通过学者的不断探索与研究,目前室内移动机器人使用最为普遍的定位算法为自适应蒙特卡洛定位算法(Adaptive Monte Carlo Localization,AMCL),该算法在局部定位方面表现良好,位姿跟踪准确[2],但随着应用发现,传统AMCL 算法在全局定位能力上有所不足。机器人每次开始定位工作时,必须给定机器人的初始位姿后,才能进行位姿跟踪。否则,机器人就必须对环境进行大量的探索观测,才能完成位姿估计收敛。人为控制机器人探索环境会增加工人负担;让机器人自主进行环境探索效率低下并具有危险性。不仅如此,由于缺乏全局定位能力,在机器人发生打滑、碰撞、人为搬运等机器人绑架问题时,机器人也无法进行位姿纠正,从而造成定位失效。这些问题与不足,都严重限制着移动机器人在实际使用中的智能性与可靠性,而通过全局定位系统进行融合辅助是一种可行的解决方案[3]。
目前,全局定位系统主要有WIFI 定位、超宽频定位(Ultra-Wideband,UWB)、超声波定位、蓝牙定位和射频识别定位等[4-5]诸多方法。如:Song Xu 等人[6]用WIFI 先进行粗定位,利用WIFI 的指纹识别信息对传统AMCL 算法的粒子进行初始化,一定程度上提高了传统AMCL 算法的粒子收敛速度。Yan Wang 等人[7]将UWB 与AMCL 算法相结合,提出了UFMCL 算法,使其能有效地进行全局定位和机器人绑架复原。考虑到超声波的低成本、定位距离远、定位精准等特点,本文决定采用超声波作为全局空间定位系统,对AMCL 算法进行融合与辅助。
1 超声波与AMCL 融合定位模型
1.1 超声波双信标定位方法
超声波是指频率大于20 kHz 的声波,其本质是一种机械波,依靠介质进行传播[8]。超声波具有穿透性强、方向性好、能量集中以及反射性好等特点,广泛应用于测距和定位领域。如图1 所示,超声波定位主要依靠三角定位原理[9],通过固定信标和移动信标之间的距离,计算被测物的空间坐标。
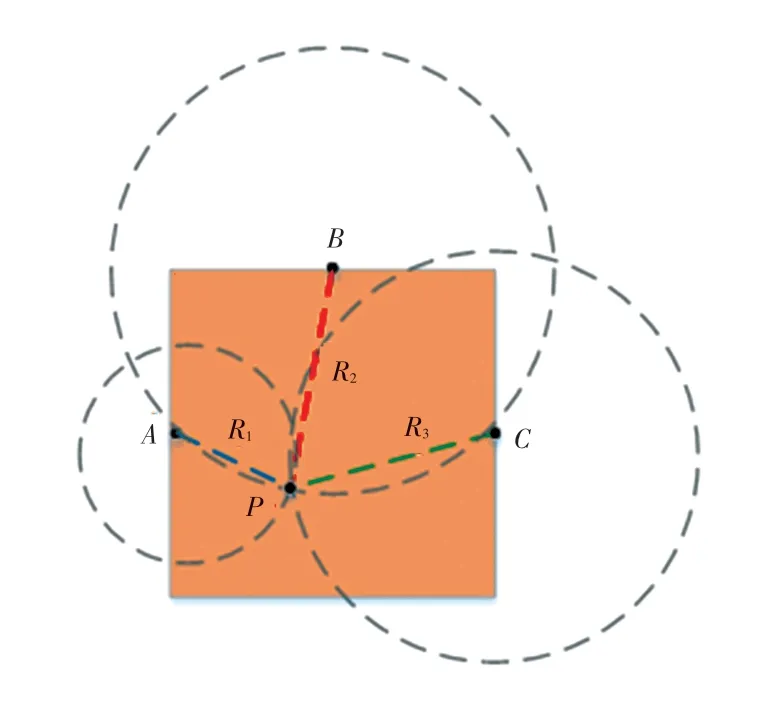
图1 三角定位原理Fig.1 Principle of triangulation
根据欧式距离,被测目标坐标计算公式为:
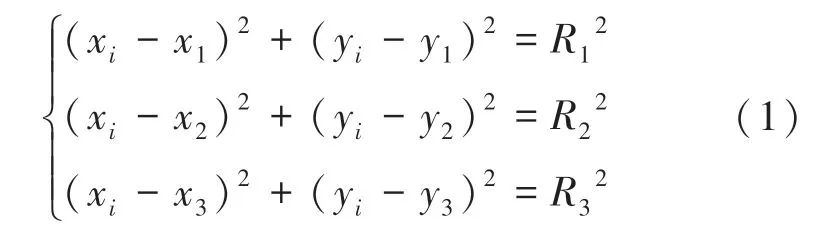
然而,传统的超声波定位系统只能反映机器人的空间位置(x0,y0),但无法得出机器人的偏航角yaw,在缺失机器人偏航角的情况下,机器人仍然无法确定所有姿态信息。因此,提出双信标定位方法。通过安装在移动机器人上的两个信标A1 和A2 的中垂线与世界坐标系的正方向夹角,来解算机器人的偏航角大小,如图2 所示。
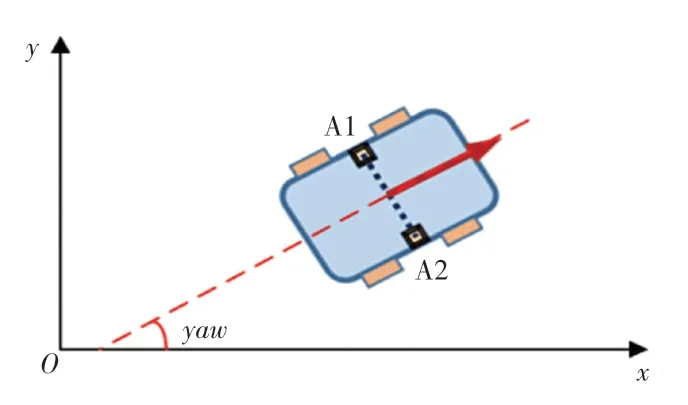
图2 双信标定位法Fig.2 Double beacon positioning method
则机器人的空间坐标和偏航角为:
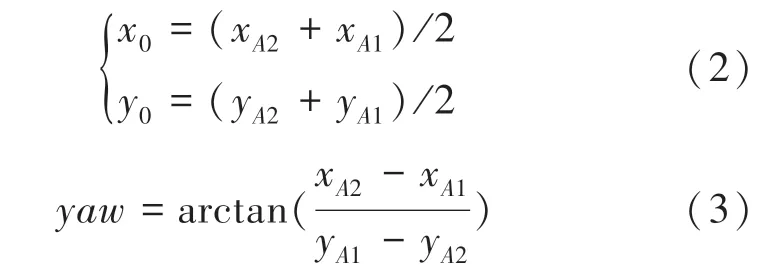
1.2 基于EKF 的超声定位与IMU 融合模型
由于超声波的多孔径效应,当超声波信标的发射端和接收端之间被障碍物干扰时,定位误差会显著增大,而惯性测量单元(Inertial measurement unit,IMU)却具有独特的检测优势[10]。IMU 不受外界干扰,检测频率很高,同时加速度和角速度检测精准,这些优势能很好的弥补超声波易受动态障碍物干扰这一不足。因此,本文采用超声波定位与IMU 融合的方案,来保证机器人运动状态下的定位。
在机器人上增加了一个IMU,x轴方向与机器人本体坐标系以及超声波定位系统坐标系的x轴一致。基于IMU 的输出量,对机器人的运动状态进行分析:
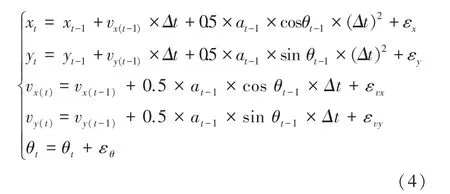
式中:(xt,yt)为机器人当前时刻位置,(vx(t),vy(t))为机器人当前运动速度,θt为机器人当前偏航角,Δt为机器人控制周期,εx,εy,εvx,εvy,εθ为空间位置、速度和偏航角的随机误差,at为机器人x轴方向加速度。
从公式(4)可以看出,状态方程为非线性模型,而EKF 滤波算法非常适合非线性高斯模型,且融合精度高,相对其他滤波器(如UKF、PF 等)计算量也较少。因此,本文采用EKF 进行状态融合。为方便融合算法分析,将公式(4)用向量形式表达为
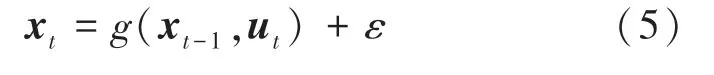
式 中:xt =(xt,yt,vx(t),vy(t),θt),ut =(at,θt),ε =(εx,εy,εvx,εvy,εθ),且ε~N(0,R)。
以上是根据IMU 传感器输出的信息完成的移动机器人推测模型,下面根据超声波定位系统建立观测模型。
根据超声波定位原理可以获得4 个直接观测量,分别为两个移动信标在平面内的坐标(xA1,yA1)和(xA2,yA2),并根据双信标定位方法,得到5 个观测量:

因此,建立的观测方程为

式中:观测误差δ符合高斯分布N(0,Q),Q为标准方差。
获得推测模型和观测模型之后,则可进行EKF融合。其实现步骤如下:
Step 1状态预测
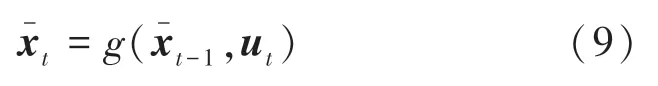
Step 2协方差预测
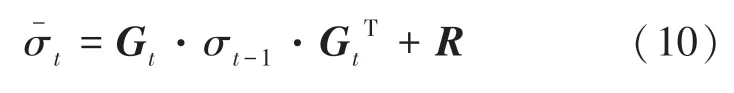
其中:
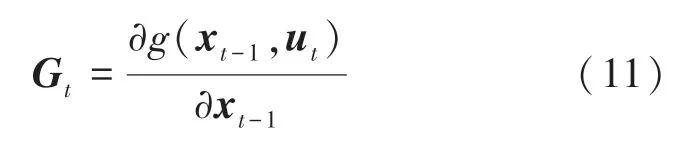
Step 3更新卡尔曼滤波增益
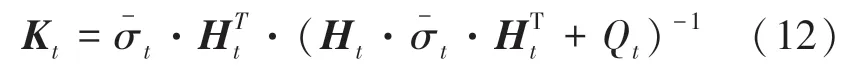
其中:
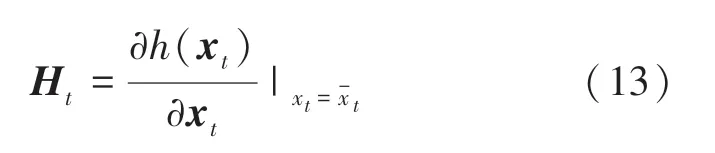
Step 4更新状态
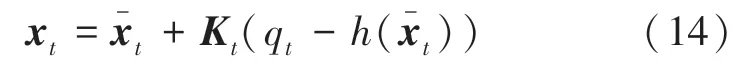
Step 5更新协方差
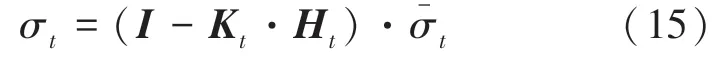
如此操作,便可以不断获得机器人的空间位姿状态以及协方差。
在matlab 中设计三角定位仿真,随机选取不共线的3 个点(5,41)、(35,10)、(53,30),作为空间中的固定信标。移动信标运动轨迹如图3 所示,将IMU 运动输出状态与超声定位结果进行融合解算。运动过程中,超声波测距引入较大误差,模仿障碍物干扰。超声波定位结果和融合定位结果如图4 所示,误差对比结果如图5 所示。
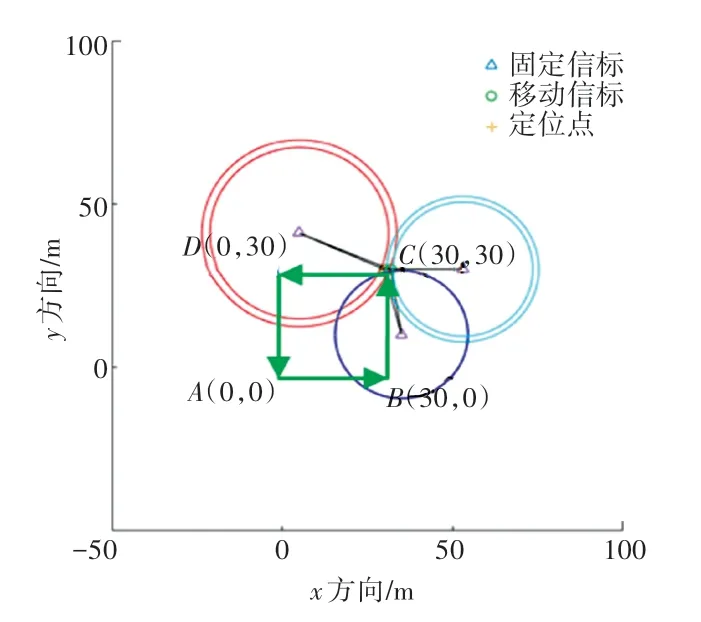
图3 机器人超声定位轨迹图Fig.3 The trajectory of ultrasonic localization
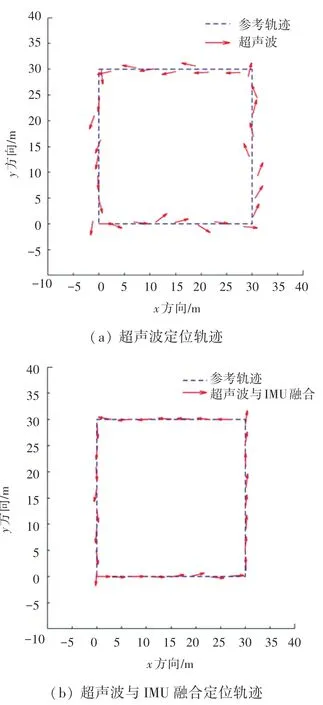
图4 仿真定位结果轨迹对比图Fig.4 Comparison diagram of simulation location result track
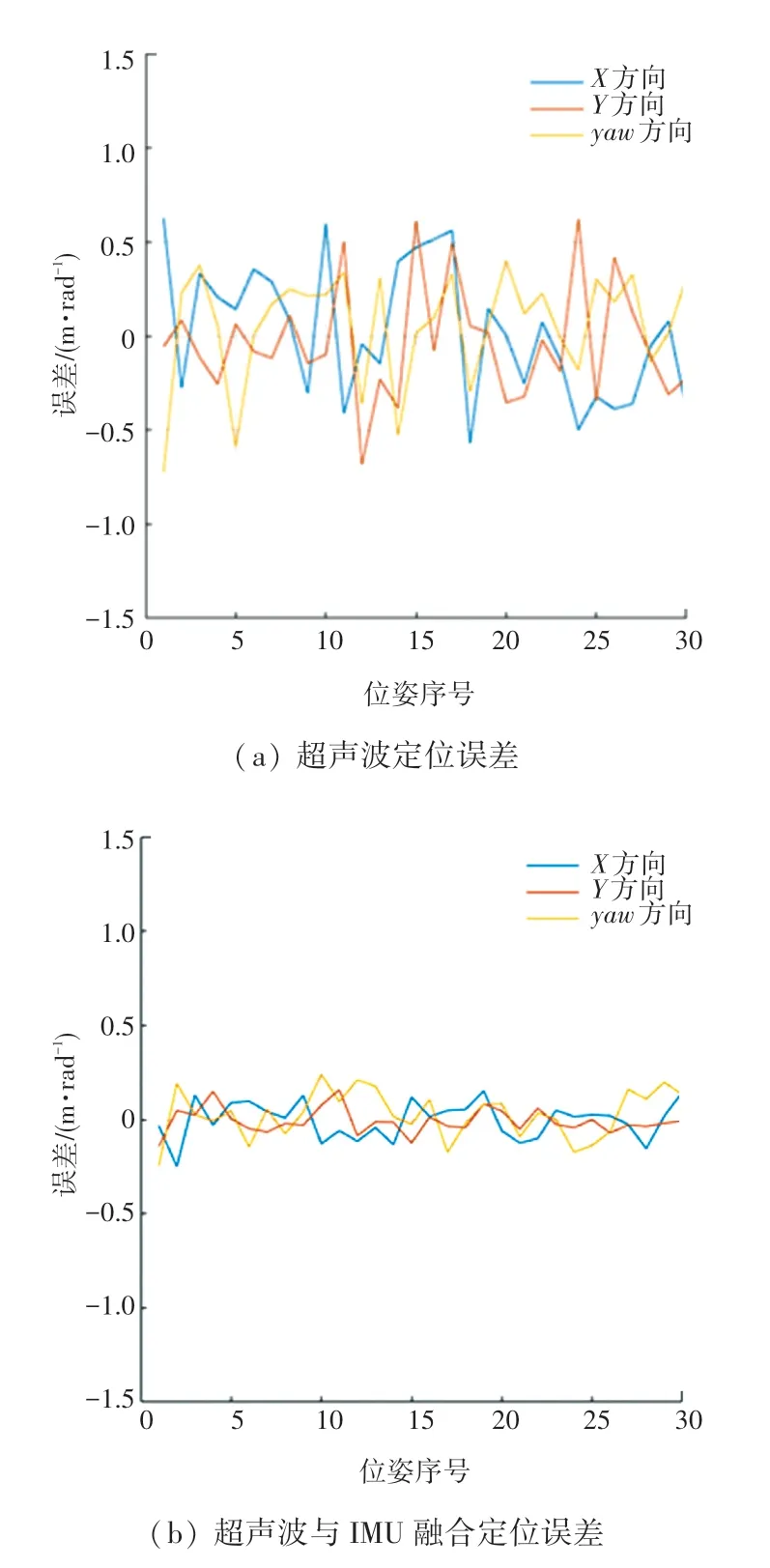
图5 仿真定位结果误差对比图Fig.5 Comparison diagram of error of simulation positioning results
从仿真定位结果轨迹对比图和误差对比图中可见,双信标定位方法虽然能解算出偏航角,获得机器人完整位姿,但易受障碍物干扰影响,而通过与IMU信息进行融合,可有效降低系统定位的误差,减小动态障碍对超声波系统的定位干扰。
1.3 超声波系统与AMCL 融合定位模型
1.3.1 传统AMCL 定位算法
AMCL 定位算法本质是基于大数定律的,该算法的定位方法可以概括为3 个阶段:
(1)粒子分布初始化阶段:定位开始时,机器人必须处于指定起点,所有初始粒子以指定起点和设定方差参数进行随机分布,这样可将全局定位问题转化成局部定位问题。
(2)粒子更新阶段:采样粒子集{x(i),i =1,2,...,N}是通过轮式里程计测量的数据分布P(xt(i)|m,x(i)1:t -1,z1:t-1,u1:t-1)而生成的。式中,m为先验栅格地图信息;z1:t-1为开始到t -1时刻的观测信息;u1:t-1为开始到t -1 时刻的运动控制变量。
采集粒子集之后,需对每个粒子进行权重评估和归一化,如公式(16):

根据权重评估和归一化的结果,对粒子集进行重采样,使之符合后验分布,且利用KLD 采样方法,来解决粒子退化问题。在KLD 采样过程中,后验概率分布被视为离散分段的单位分布,表示目标分布的子空间。通过引入KL(Kullback-Leibler)散度,也叫相对熵。KLD 采样方法用一个公式描述估计的概率分布与真实的概率分布之间的近似度,并将两者误差限制在一定范围内。公式(17)为推导出的KLD 所需要样本的最小值Nkld:
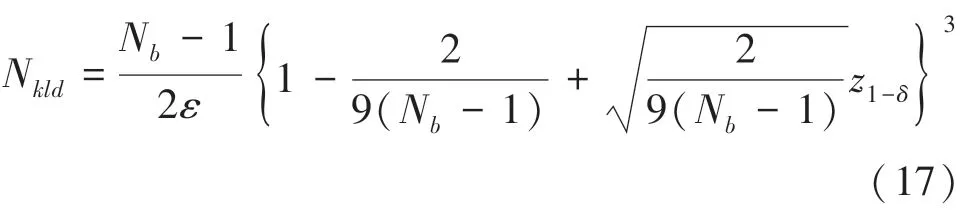
其中:Nb为样本所占子空间的个数;ε为目标分布误差的最大值;1-δ为误差小于ε的概率。
当生成的粒子数大于Nkld时,采样过程停止。
(3)位置确定阶段:重复步骤(1)、(2),不断更新机器人采样粒子集,最后以粒子位置的最大权重作为机器人的估计位置。即系统在t时刻的状态由公式(18)得出:
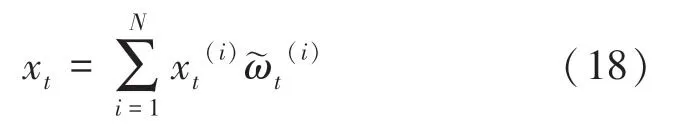
算法最终的建议分布越接近目标分布,粒子滤波器就越好。
1.3.2 改进超声定位与AMCL 融合定位算法
由于传统AMCL 定位算法只在局部定位时较为准确,而在全局定位以及机器人绑架问题上仍存在缺陷。因此,提出将改进的超声波定位系统与AMCL 定位算法进行结合。
首先,由超声波定位系统进行三点定位和双信标偏航角解算,从而获得移动机器人包括空间位置与偏航角等所有姿态。然后,对移动机器人进行工作状态判断:如果移动机器人处于静止状态,则将求解出的位姿用来对AMCL 算法的定位粒子进行初始化。通过超声波定位系统提供的全局定位信息作为参考,可省略传统AMCL 算法在全局定位过程中大量的运动探索,来完成粒子收敛的过程,且使得全局定位过程更加安全、高效。如果移动机器人处于动态,将直接输出超声波系统解算出的机器人位姿,并与车载IMU 传感器进行融合,从而保证超声波定位系统的输出结果不受动态障碍物影响。最终在运动过程中,超声波与IMU 的初步融合结果,进一步与AMCL 的定位结果通过EKF 滤波器进行融合,来纠正AMCL 可能发生的机器人绑架问题,保障系统定位的可靠性。
2 实验验证
2.1 机器人平台及实验环境搭建
机器人平台如图6 所示,上面分别安装超声波雷达、轮式里程计和激光雷达,这些传感器共同完成对环境空间的感知,最终确定机器人的空间位置和姿态。超声波雷达装在车顶,可保证信号的接收,激光雷达高度约为0.2 m,可识别定位空间中绝大多数障碍物。机器人搭载工控机,内存为8 GB,处理器为Intel 的i7-8650U,1.9 GHz。系统为Ubuntu14.04,各类实验结果输出主要使用了ROS 系统下的Rviz 可视化工具。

图6 实验平台组成Fig.6 Composition of the experimental platform
实验采用Marvelmind robtics 公司的HW4.9 型超声波信标,该信标有效探测距离可达30 m,定位精度为±5 cm,调制器可对半径150 m 以内所有信标进行时间同步;温度感应器,可针对当前室温进行温度补偿;工作频率可调。信标安装布局以及机器人运动轨迹如图7 所示。固定信标、移动信标和激光所扫描障碍轮廓如图7(a)所示。定位系统以20 Hz的频率不断更新输出定位坐标,机器人在实验室环境下沿着A、B、C、D 4 点所围成的矩形路径进行运动,如图7(b)所示。
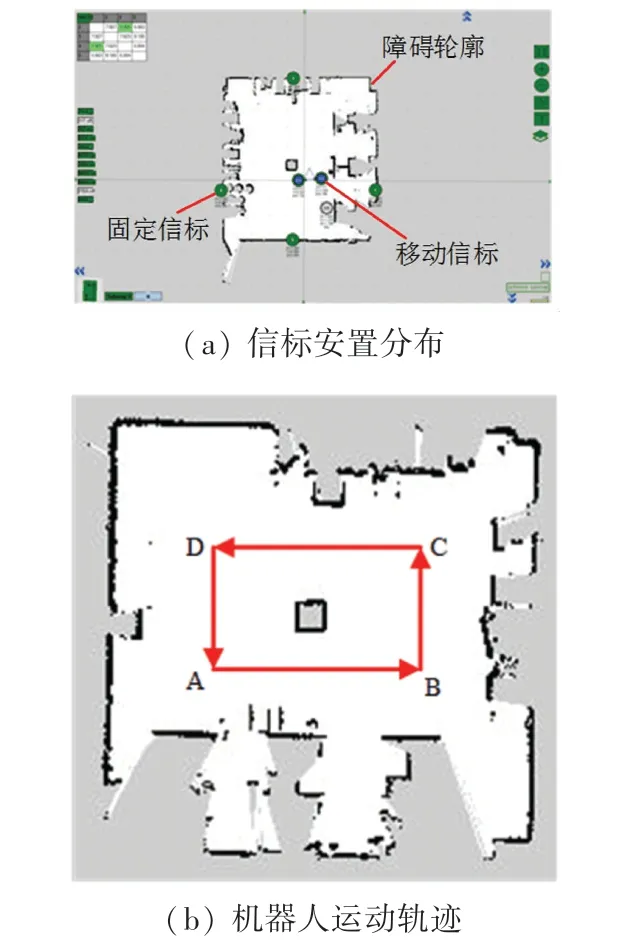
图7 超声波信标分布和机器人轨迹图Fig.7 Ultrasonic beacon distribution and robot trajectory diagram
2.2 实验结果与分析
2.2.1 实验一:局部定位实验
超声波定位系统单独定位轨迹及与IMU 融合后的轨迹如图8 所示。
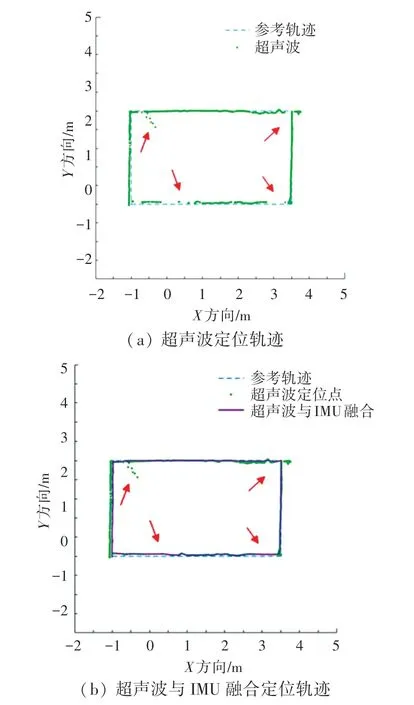
图8 超声波定位系统定位轨迹图Fig.8 The positioning trajectory diagram of Ultrasonic positioning system
可以看出,超声波定位效果较好,定位精度在厘米级别,但在箭头所指的动态障碍物干扰处,发生了定位异常,出现定位丢失或者较大的跳变。而将超声波定位结果与IMU 进行融合后,IMU 的测姿连贯性对超声波定位的定位异常产生了很好的约束作用,提高了超声波定位系统的定位可靠性。
如图9 所示,实验中也使用了传统AMCL 算法进行定位,传统AMCL 算法可以获得较好的定位结果,但仅仅依靠里程计推测航迹,激光雷达进行观测,当环境观测的匹配度降低时,依靠采样粒子所解算出的位置差会变大,在本次实验中最大定位误差达到了25 cm。而本文提出的超声波与AMCL 融合定位算法的解算结果与参考轨迹重合度较高,整个定位过程位姿跟踪准确。通过EKF 滤波对超声波定位系统的输出结果与AMCL 定位结果进行融合,增强了整个系统的定位鲁棒性和准确性。
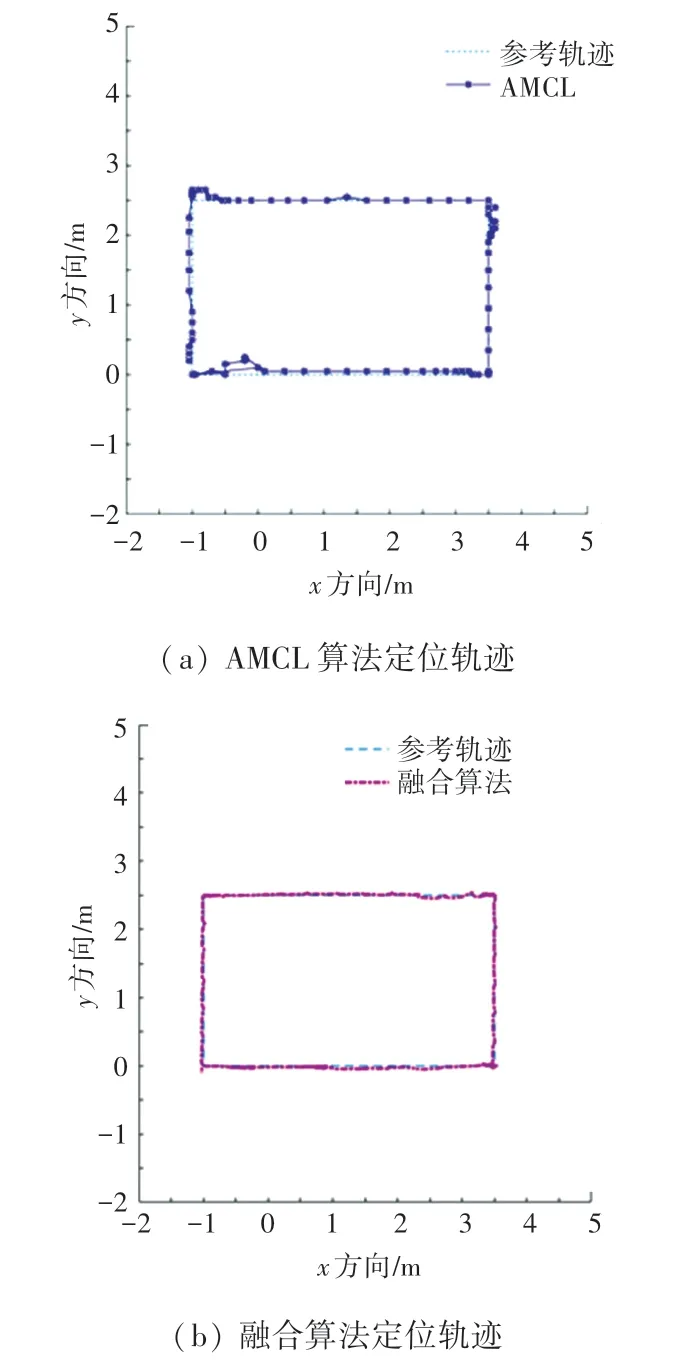
图9 AMCL 定位和融合算法定位轨迹图Fig.9 AMCL localization and fusion algorithm localization trajectory diagram
本文融合算法与单一传感器定位、传统AMCL算法定位对比效果如图10 所示。表1 中给出了里程计、超声波、AMCL 定位以及本文融合定位算法在X和Y方向上的误差统计。可以看出,融合算法的定位误差小于3 cm,证明了融合算法在局部定位方面的优势。
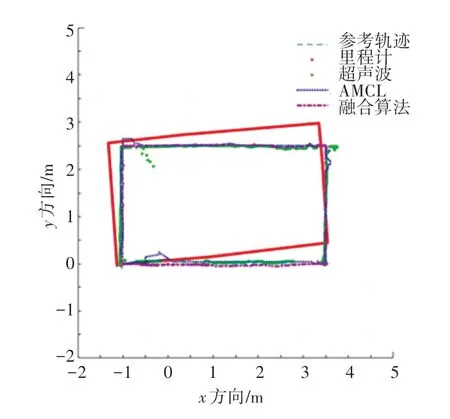
图10 融合算法与其他定位方式轨迹对比图Fig.10 Comparison between fusion algorithm and other positioning methods
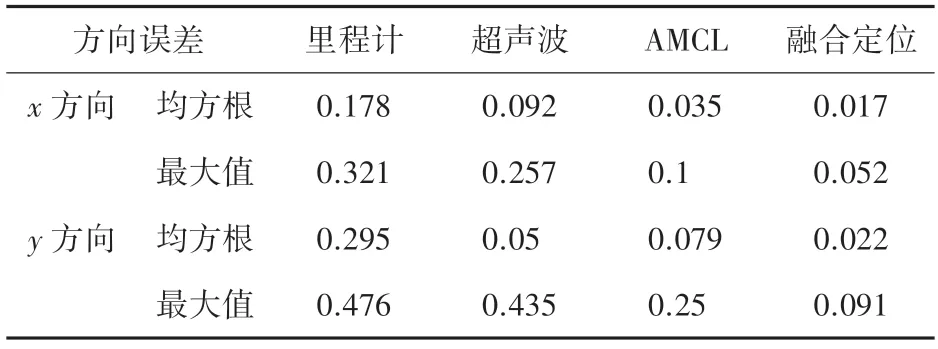
表1 各种定位结果误差统计/mTab.1 Error statistics of various positioning results/m
2.2.2 实验二:融合算法的全局定位时间测试
在地图中任意选择10 个位置进行定位,分别记录在单纯依靠AMCL 算法的全局定位时间和融合算法下的定位时间。实验结果见表2。
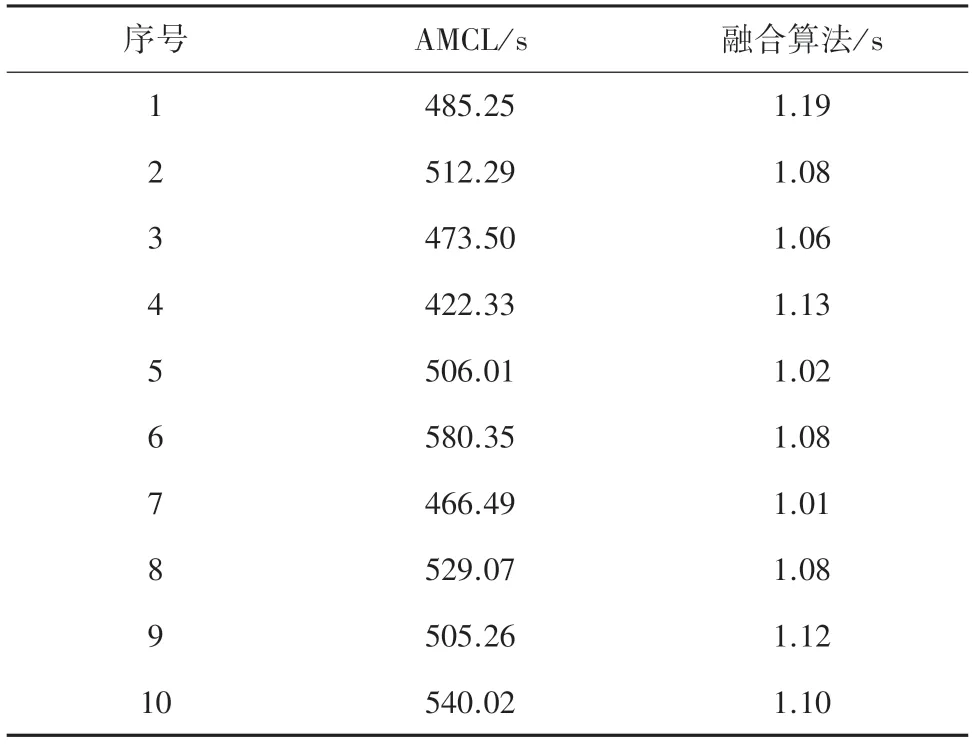
表2 改进算法定位时间比较Tab.2 Comparison of location time of improved algorithm
由对比结果可见,本文提出的融合超声波传感器的定位算法可以大大节约传统AMCL 定位算法的粒子收敛时间;通过超声波信息更新全局定位,也避免了机器人在粒子收敛过程的运动探索,增强了移动机器人定位的智能性与安全性。
3 结束语
本文设计了一种融合超声波信息的改进自适应蒙特卡洛定位算法,解决了传统AMCL 算法在全局定位方面效率低、不成功等问题。在本算法中,当进行全局定位时,通过双信标解算机器人姿态,并与IMU 进行信息融合,得到了可靠的全局定位信息,依靠此信息可迅速完成AMCL 算法的全局定位粒子初始化,避免了传统AMCL 算法漫长的粒子收敛过程,大大节约了机器人全局定位时间。同时,改进的超声波全局定位信息与AMCL 定位进一步融合,在一定程度上提高了位姿跟踪的定位精度,改善了定位效果,也保障了最终定位的稳定性与可靠性。

