基于车辆悬架的载荷设计方法

程 凯，孟凡亮，张关良，刘 杨

（奇瑞汽车股份有限公司 汽车工程技术研发总院，安徽 芜湖 241009）

目前行业对于轻量化的研究工作主要是从结构设计及新材料应用上着手，结构上的设计思路一般采用拓扑优化、形貌优化、尺寸优化、灵敏度分析等手段，寻求结构的最佳传递路径及敏感因素。如文献[1]采用拓扑优化的方法应用于控制臂的轻量化设计。新材料应用主要包括高强度钢材[2]、铝合金材料。文献[3]阐述了汽车底盘用铸造铝合金的研究进展。而结构的设计输入是载荷，因此，结构轻量化设计的源头应该是载荷的设计，更合理的载荷分配是结构轻量化的关键因素之一，载荷设计的核心又在于硬点的优化，合理的硬点分布应该既能满足运动学特性和动力学特性（Kinematics Compliance, KC）要求，又要有合理的载荷分配特性。目前载荷设计的文献并不多见，而悬架硬点的优化相关的研究较多，其主要以KC性能为目标。文献[4]采用Insight优化软件，考虑KC边界对悬架硬点进行设计，而文献[5]在仿真分析的基础上，针对不合理的结构设计参数，利用Adams/Insight模块进行基于设计变量灵敏度分析的优化设计，文献[6-9]也考虑了KC及操稳边界，以上均没有考虑载荷的设计边界。因此，本文阐述了一种载荷设计的方法，将载荷分析工况引入试验设计（Design Of Experiment, DOE）中，以悬架硬点为变量进行载荷优化设计，并且通过理论分析对结果进行解读，为结构轻量化设计提供基础，也为悬架设计开拓思路。

首先采用Adams软件建立悬架动力学模型，分析载荷及KC工况下的响应，然后通过Optimus及Adams软件求得优化近似模型，基于近似模型进行最优化求解，载荷设计方法流程如图1所示。

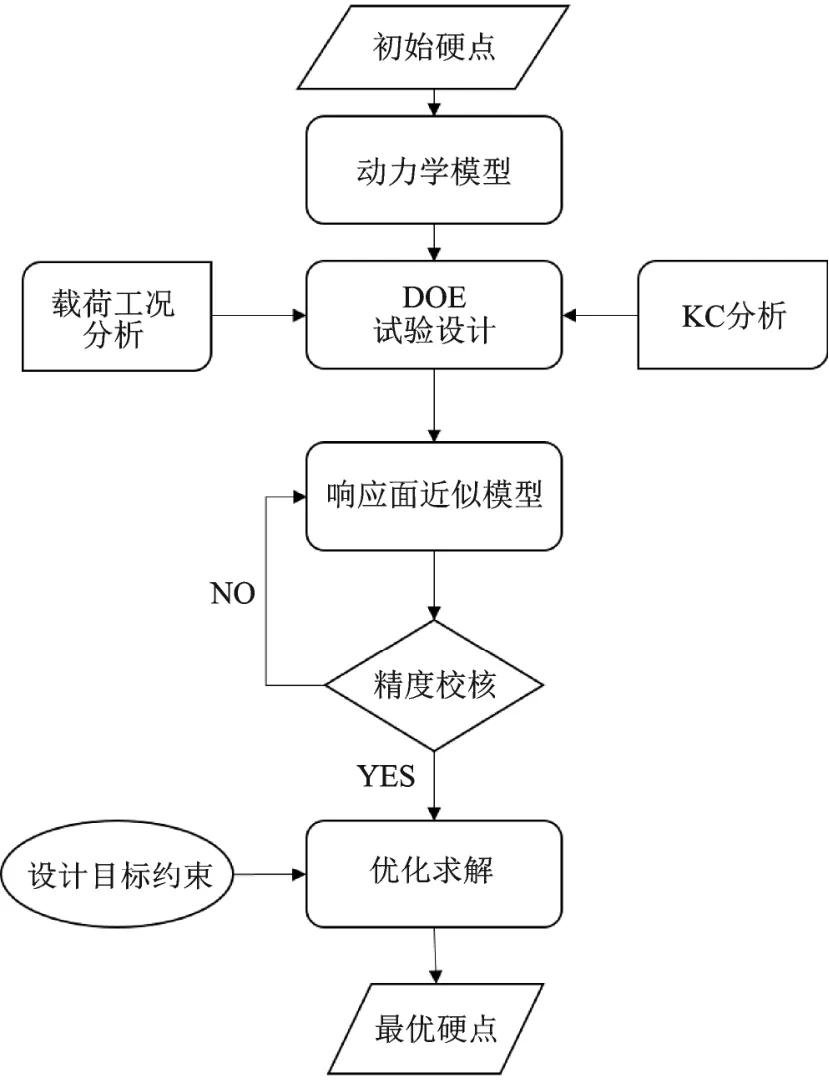
图1 载荷设计流程图

1 载荷分析及优化目标定义

分析采用的悬架形式为五连杆结构，如图2所示，主要包括前上摆臂、后上摆臂、前束调节杆、前下摆臂、后下摆臂，该悬挂形式主要具备两个重要的特点：一方面悬架可调校性能较强；另一方面由于没有纵向摆臂支撑（相比四连杆形式悬挂），车辆直线行驶过程中纵向载荷大部分会转化成侧向载荷，这样就会使车辆具备良好的平顺性能，但这些载荷主要由杆系及副车架吸收，会使悬架杆系结构承载力增加，尤其是车辆在高速行驶中冲击障碍物时，杆系载荷会急剧增加，如硬点及结构布置不合理极容易产生大载荷，导致强度耐久问题。

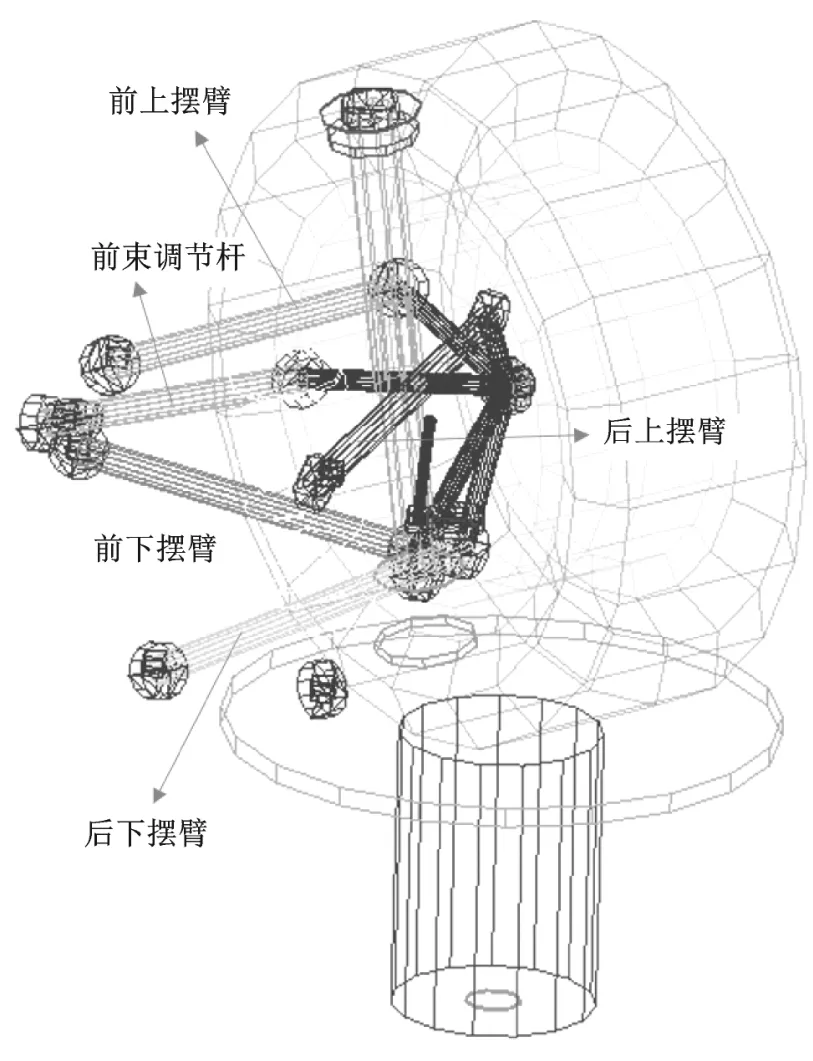
图2 悬架动力学模型（整车坐标系）

1.1 载荷分析

在悬架开发过程中，载荷一般通过动力学模型提取，本文采用汽车行业中常用的Adams多体动力学软件搭建动力学模型，在car模块中分别建立悬架系统模型、稳定杆系统模型，将其装配成后悬架系统模型。模型中所需硬点坐标均从计算机辅助设计（Computer Aided Design, CAD）数据中提取，所需弹性元件刚度，如弹簧、衬套、缓冲块均采用实测数据。载荷工况采用悬架级静载荷工况进行分析，主要考虑的载荷工况为纵向冲击工况、垂向冲击工况、侧向冲击工况。由工程经验可知，汽车以60 km/h行驶冲击障碍物时，纵向冲击载荷大约为7g满载单轮轴荷，垂向冲击工况约为6g满载单轮轴荷，而出现甩尾撞击障碍物导致的侧向冲击约为4g满载单轮轴荷，因此，以此为主要引入的边界条件进行后续优化设计工作。标优化进行设计。

1.2 目标定义

悬架共有5根杆系，应属于多目标优化问题。但由于多目标优化方法一般通过加权分配方法进行求解，加权系数需要人为给定，这样会导致优化带有一定的主观性，另一方面各目标之间与变量相互耦合会使目标函数的求解精度降低，因此，建议采用单目标进行优化设计。

2 载荷优化设计

2.1 DOE

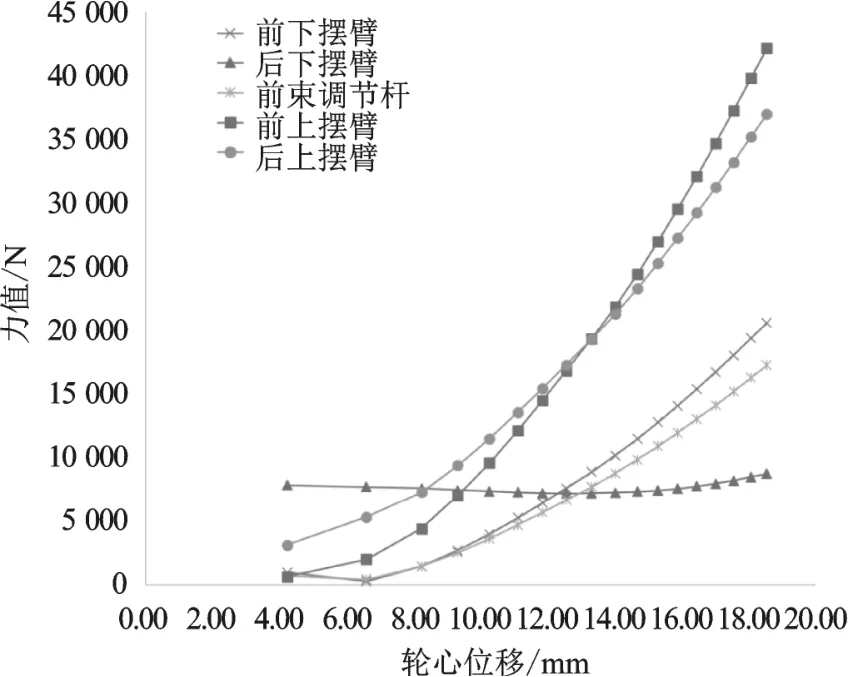
图3 摆臂结构受力曲线

DOE可以理解为一种抽样试验方法，主要目的是通过抽样部分样本来尽可能表达总体样本的特性信息。抽样方法主要包括全因子法（Full Factorial Design）、田口法（Taguchi Design）、部分因子设计法（Fractional Factorial Design）、拉丁超立方方法（Latin Hypercube Design）等，综合效率及抽样精度，本文采用拉丁超立方法进行抽样设计，共计100个样本点。

2.2 响应面模型

图3为悬架在纵向工况作用下杆系结构的受力情况。随着载荷的增加上摆臂受力明显有上升趋势，主要原因是轮心距离上摆臂Z向高度相比下摆臂小，因此，承受纵向冲击时，上摆臂承受载荷会更大，而其他杆系载荷变化有限，并且本身载荷基数较小。而两个上摆臂的受力趋势一致，属于正相关，因此，优化时可以将前上摆臂载荷作为优化目标，这样就可以将结构简化为单目

工程方面从效率及精度上综合考虑，优化会基于响应面模型进行，DOE求解完成后就可以开展响应面模型的建立工作，响应面是一种近似模型，通过不同的数学模型来表达输入和输出变量的关系，由于硬点变化与KC性能强相关，因此，为了保证优化结果的合理性，也同时需要考虑KC仿真工况，本文重点考虑了侧向力、平跳、侧倾、制动力这四种KC工况，以侧向力转向、侧向力外倾、侧向力轮心位移、垂跳前束、垂跳外倾、侧倾前束、侧倾外倾、制动力外倾、制动力转向、制动力轮心位移这10个KC性能指标作为优化约束边界。将5个摆臂内点x坐标作为优化输入变量。为了提升优化效率，将杆系结构近似为二力杆结构，因此，输出变量为杆系轴向载荷及KC性能目标，详细如表1所示。

表1 输入及输出变量

采用基函数差值方法生成近似响应面模型，需要表达的原函数为f(x)，该函数在离散点X={x1,...,xn}的值为(f1,...,fn)。

假设近似函数为S(x)

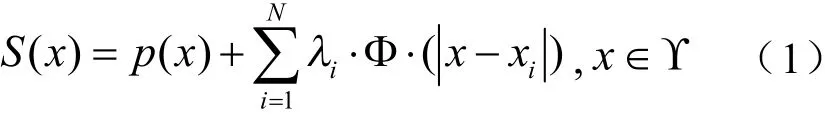
式中，p(x)表示k阶多项式；λi表示权重系数；Φ代表基函数，基函数形式为Φ(r)=r3.logr，|x-xi|表示x与离散点的距离差值。

通过式（1）可求得响应面模型。

近似模型的精度对于后续的优化工作至关重要，合理的近似模型能够高精度、高效率地寻求最优解，近似模型的精度一般通过式（2）表示：

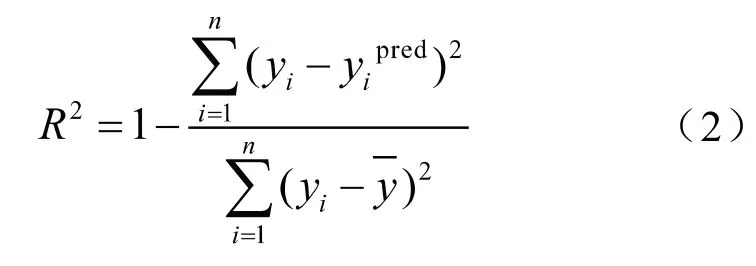
式中，R2为预测残差平方和；yi为样本点仿真结果；为响应面预测结果；y为样本点仿真结果均值。

R2可以用来表示近似模型的精度，R2越接近1，说明近似模型的精度越高，实际工程应用中一般达到R2＞0.9就可以认为响应面模型的精度可以达到应用要求。表2列举了部分关键变量的残差平方和，可知关键输出变量的R2均接近1，说明基函数方法可以很好地近似原始模型，响应面模型精度较高，可以基于该模型进行优化求解。

表2 响应面残差值

2.3 优化求解

优化问题的数学模型可以表示如下：

（1）设计变量：X={x1,x2,x3,...,xm)，本文设计变量如表1所示；

（3）目标函数：Target=min(f(x))，由于前上摆臂在静载考察工况下受力最大，因此，将其作为优化目标；

（4）边界约束：gj(x) ≤ 0j=1,…,n，本文约束函数为10个KC性能指标。

目标优化算法主要包括局部优化方法、全局优化方法两大类。局部优化求解的数学模型包括连续二次规划求解法、二次非线性求解方法、随机搜索方法等。全局优化求解数学模型主要包括差分算法、神经网络算法、遗传算法、进化算法等。本文采用全局进化算法中的自适应进化算法（Self-adaptive Evolution）求解。

优化后硬点调整如表3所示，优化结果如表4所示，载荷工况共计15个载荷考察指标，其中有10处载荷指标均有降低，剩余5处有一定增加，但由于本身载荷基数并不高，并不是最大载荷工况，并不影响结构设计。整体来看优化结果较为明显，尤其是纵向冲击工况，该工况中前束调节杆轴向载荷可降幅44.4%，前上摆臂降幅27.3%，后上摆臂降幅18.2%。由于上摆臂结构承载力基数较大，因此，最大降幅可达9 979 N，这对于结构减重和耐久设计均有重要意义。而从约束的KC指标上看，调整硬点后变化较大，但由于优化过程中给定了KC的边界约束，整体还处在合理目标范围内，尤其是垂跳前束性能相比原始状态也得到了提升，并没有因为载荷降幅而导致KC性能下降，整体优化较为合理。

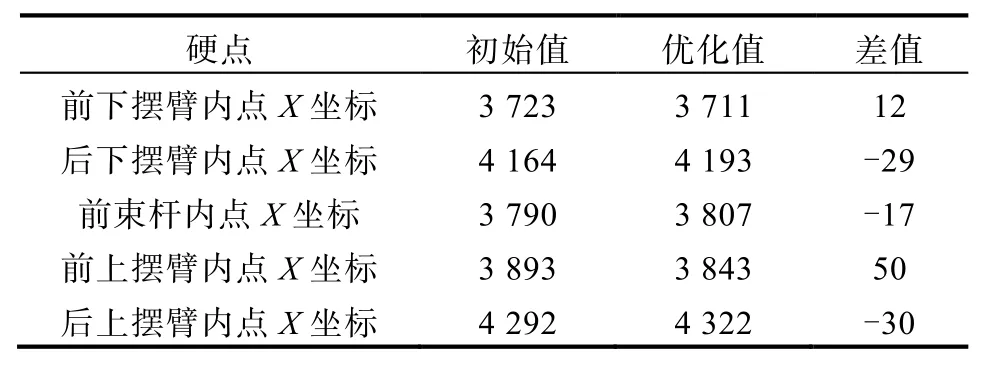
表3 优化后硬点调整

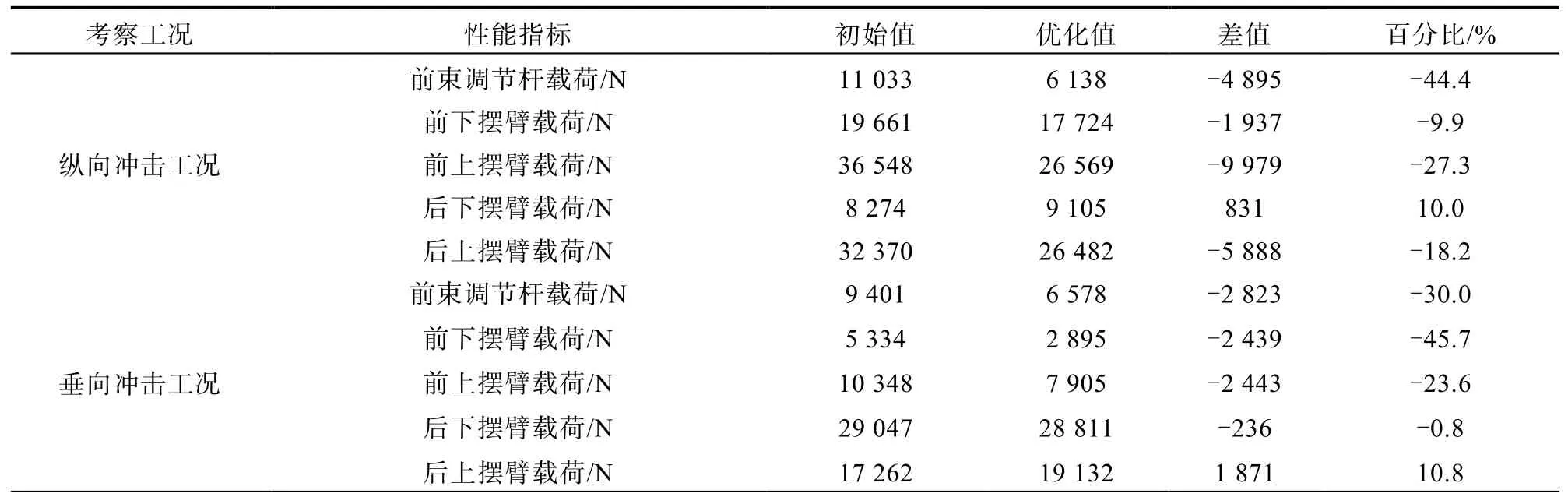
表4 优化结果

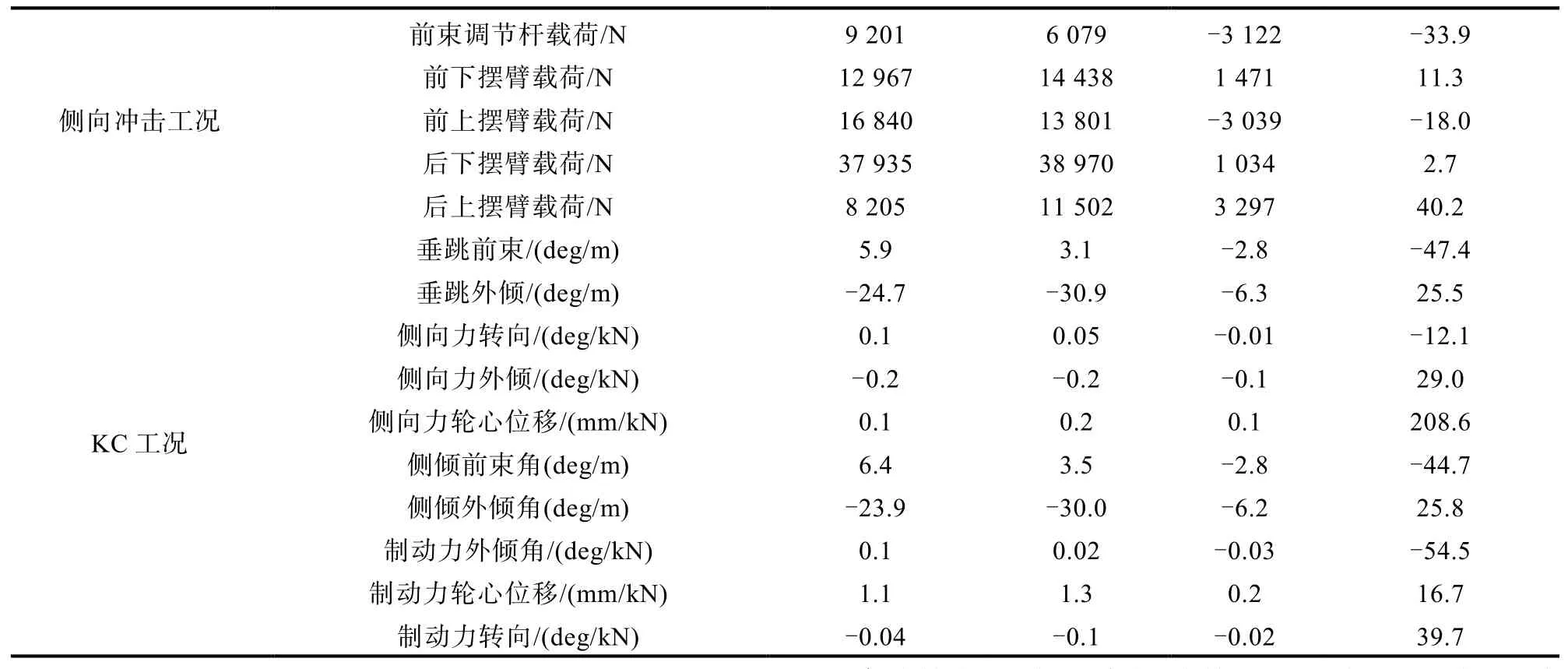
表4 （续）

3 理论分析

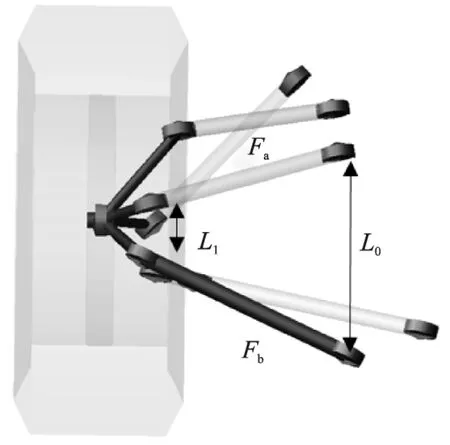
图4 悬架模型简图

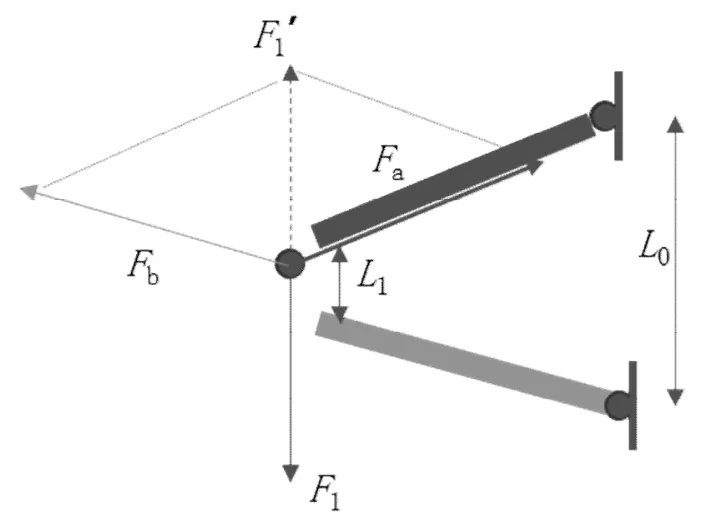
图5 受力分析

由优化结果可知，纵向冲击工况优化效果最明显，因此，以该工况为例，进行理论分析，从表3中可以明显看出上摆臂x方向坐标的变化最大，是最敏感因素。具体可以观察到，优化后前上摆臂内点x坐标变小，后上摆臂内点x坐标变大，如图4所示，就是L0的跨度变大，也即L1/L0的比例关系会影响结构的受力分配。参考图5，将摆臂结构简化为二力杆结构进行分析，图中F1为输入外载荷，Fa、Fb相当于摆臂结构，由于杆系两端均为衬套或者球头连接，所以可以简化为二力杆结构，因此，可认为只承受轴向载荷。根据力的平衡原理，输入的载荷F1需要与杆系的合力平衡，而L1/L0的比例越大会导致Fa、Fb的合力越小，想达到与F1平衡则需要二力杆承受更大的轴向力载荷。如果想降低Fa、Fb的载荷需要减小L1/L0的比值，通过减小L1或者增大L0距离可以实现，由图6可以看出，随着比值的降低，载荷明显降低，而且下摆臂的受力变化并不大，本文优化前为36%，优化后L1/L0比例为29%。

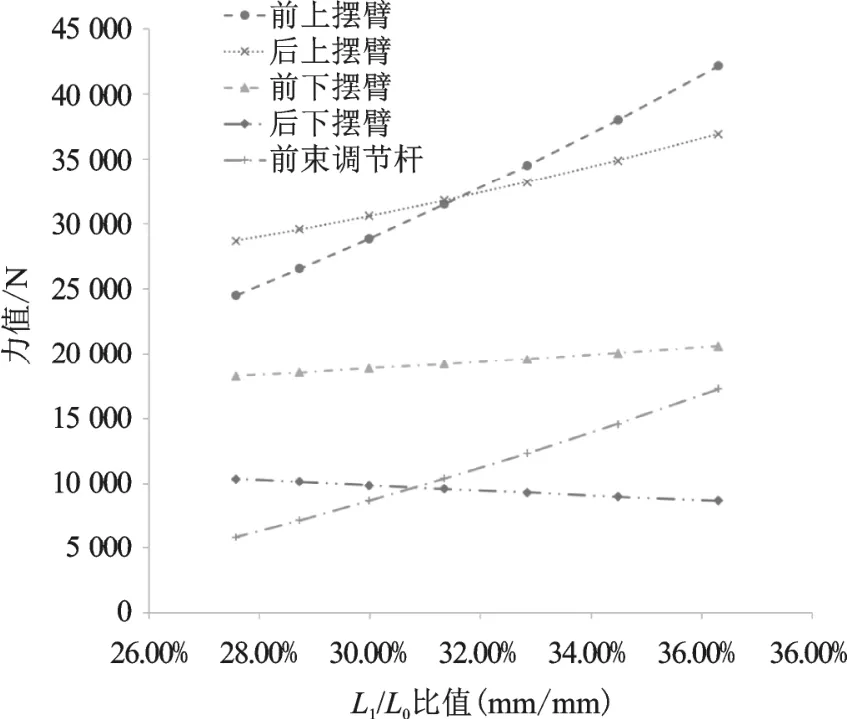
图6 杆系轴向载荷和比值关系

表5统计了竞品6款相同悬架类型的车型，可以发现，比值都小于35%。所以悬架设计时应尽可能地去降低比值，如果前后两个杆件过分接近平行关系会导致轴向载荷过大，不利于结构轻量化设计，同时也会增加结构及衬套的耐久风险。

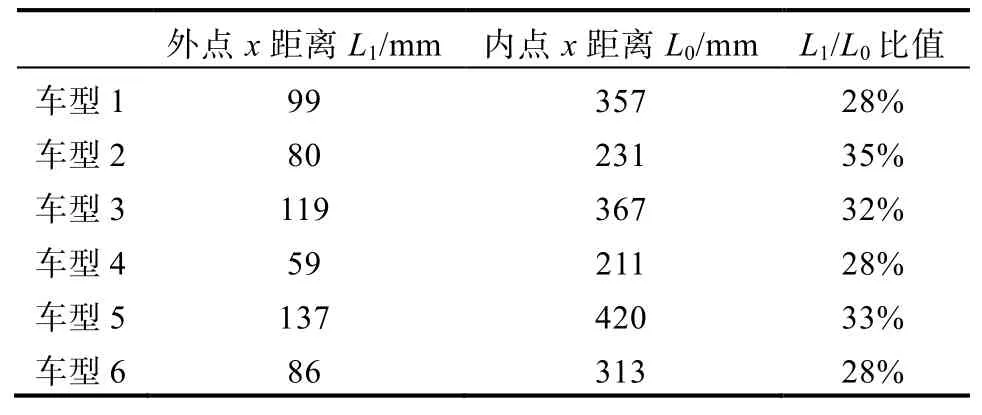
表5 不同车型比例关系

4 结论

悬架硬点优化目前大部分都是基于KC性能指标开展的，硬点与载荷相关的设计并没有得到足够的重视。本文阐述的载荷设计方法，优化中重点引入了载荷分析工况，并且同时考虑了KC边界，对悬架结构进行DOE仿真分析，采用拉丁超立方进行样本抽样，采用基函数差值方法得到系统的近似模型，以此为基础进行载荷的最优化设计。采用该方法优化后，载荷降幅明显，最大降幅可达到44.4%，悬架的硬点分布更加合理，同时满足载荷及KC要求。由于多连杆悬挂的特有杆系形式，在载荷分析过程中可以将其简化为二力杆进行受力研究，杆系之间的比例关系对于载荷分配至关重要，悬架设计中应该重点研究。

本文阐述的分析方法也有一定的局限性，主要原因是该方法是基于实际项目总结而来，因此，根据项目经验简化了一些边界范围约束，如优化变量的范围，只考虑了整车x方向坐标的影响，而并没有考虑y、z坐标的影响，除此之外，载荷设计影响因素并不只有硬点，一些弹性元件的影响也较大，如衬套刚度、缓冲块的刚度，减震器阻尼，这些变量都可以作为后续载荷设计的研究工作。