基于AHP 的战时多目标弹药调度模型优化

李 凯，刘铁林，张 亮，李明雨

（1.陆军工程大学 石家庄校区，河北 石家庄 050000；2.32670 部队，辽宁 朝阳 122000；3.陆军步兵学院 石家庄校区，河北 石家庄 050000）

0 引言

弹药调度是战时弹药保障的重要组成部分，直接影响任务部队弹药能否及时、准确、可靠地获得弹药供应，一定程度上，弹药调度直接影响战争进程和结局。现代战争作战节奏快、弹药消耗巨大、战场环境复杂多变、弹药保障任务紧迫，通常是多个弹药储备点保障多个弹药需求点，增加了弹药调运组织的难度，以往依靠后勤指挥员的直觉和经验制定的调运方案已不能满足现代战争对于弹药保障快速、高效、准确的要求。针对弹药调度相关问题，国内许多学者开展了针对性研究。其中文献[1]建立了基于混沌粒子群优化算法的突发事件应急物资调度优化模型；文献[2]利用AHP-熵权逼近理想解的排序方法对区域油料保障力量部署方案进行了优化。文献[3]运用多目标遗传算法对维修保障资源调度进行了优化。文献[4]针对舰载机调度供求点多的特点，用蚁群算法对调度方案模型进行了求解和优化。文献[5]针对后方仓库弹药配送的车辆调度问题，在时间窗约束条件下，构建相关数学模型，并用改进的遗传算法对其进行求解。上述调度优化方法依赖于相关指标的精准描述，且指标确定受到评价者主观认识和偏好影响较大，在实际问题应用中操作性不强，使得决策者无法对弹药调度方案作出快速正确决策。基于此，本文提出运用层次分析法（AHP）确定目标函数权重，构建战时条件下多目标弹药调度模型。运用运筹学、系统科学等基本理论和方法，探索战时弹药调度方案的制定方法既是信息化条件下弹药保障的要求，也是提高弹药保障资源利用效率的必然选择。

1 战时多目标弹药调度模型构建

1.1 战时多目标弹药调度问题描述

战时弹药运输，存在相关信息不确定、保障需求不具体、道路状况变数多等困难，加上战场环境的动态变化，保障人员很难准确确定弹药需求的数量及弹药由储备点到需求点所耗时间。因此，本文将弹药保障需求、弹药供应时间、弹药运输成本等作为不确定因素，运用区间理论建立约束条件，构建战时多目标弹药调度模型。

为了便于研究问题，假设有n 个弹药储备点，设弹药储备点的现实供应量为Si，最大供应量为其中i=1,2,…,n；弹药需求点有m 个，设需求点的现实需求量为dj，j=1,2,…,m。为便于表示，将单位弹药从储备点Si到需求点dj的时间记作tij，弹药需求点dj的目标期望时间值（即弹药保障分队指挥员希望弹药从储备点到需求点的标准时间）为tj。从储备点Si运输至需求点dj的弹药数量记作xij，设其单位弹药调度成本为cij，则弹药调度成本表示为cijxij，将弹药从储备点顺利运输到需求点的概率为pij，目标期望p0；其中dj、tij为不确定区间数。

1.2 战时多目标弹药调度问题假设

（1）所有弹药储备点的弹药储存量充足；（2）只考虑陆路运输弹药；（3）弹药需求量为区间数；（4）弹药运输时间为区间数；（5）只考虑弹药数量，不考虑弹药种类。

1.3 建立战时多目标弹药调度模型

确定目标函数：

其中：式（1）表示以弹药物资总延误时间最短为目标函数；式（2）表示以弹药储备点至弹药需求点调度成本最低为目标函数；式（3）表示弹药顺利由储备点运输至弹药需求点的最大期望值为目标函数。

确定约束条件：

其中：式（4）表示弹药供应总量等于弹药需求总量；式（5）表示每个弹药需求点收到的弹药量即为需求点的需求量；式（6）表示储备点弹药运输至需求点过程中弹药无损失；式（7）弹药储备点总供应量小于其最大储备量；式（8）弹药调度过程安全、顺利；式（9）表示从弹药储备点Si到弹药需求点dj的弹药大于等于零。

2 战时多目标弹药调度模型求解过程

多目标规划是研究多个目标函数在一定约束条件下的最优化。常用求解方法有三类：第一类是化多为少方法，就是将多个目标通过某种方式转化为便于求解单目标或双目标，有主要目标法、线性加权法和理想点法等；第二类是分层序列法，即把目标按其重要性排序，后一目标分别依据前一目标最优解集内的元素求最优解，直至得到各目标的共同最优解；第三类是层次分析法，适合用于目标结构复杂且缺乏必要数据的情况，是一种把定性分析与定量分析相结合运用的多目标决策方法。本文将第一类中的线性加权法与第三类层次分析法相结合，对模型进行求解[6-9]。具体求解过程如图1 所示。

图1 基于AHP 的战时多目标弹药调度模型求解流程

2.1 确定目标函数和约束条件

根据不同情况下的实际需要，确定模型的目标函数和相关约束条件，为方便计算，记目标函数：

2.2 确定目标函数的相对权重

运用层次分析法，求解各目标函数权重系数，详细计算见文献[7]。现将具体步骤简述如下：

（1）建立目标函数的AHP 模型。通常建立三层结构，第一层为经目标函数加权合并后的效用函数，第二层为目标函数，第三层为方案层。

（2）构建目标函数判断矩阵。为将目标函数两两比较关系量化，引入1～9 标度法（见表1），aij为要素i 与j 的重要性比较结果，目标函数两两比较结果构成的矩阵称作判断矩阵，有如下性质：。比例标度如表1 所示。

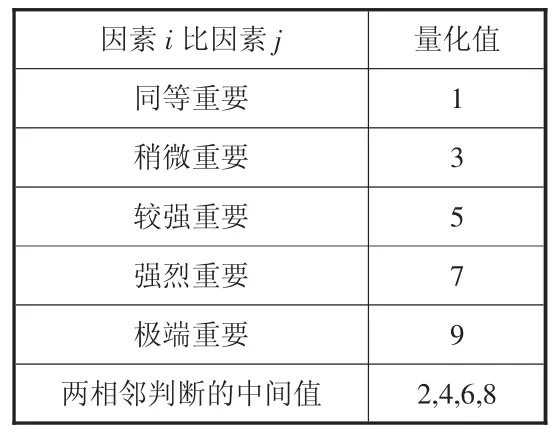
表1 比例标度表

（3）运用yaahp 软件计算各目标函数权重，记对应目标函数的权重为ωk（k=1,2,3），且有

2.3 运用线性加权法，构建新的目标函数

线性加权法具体可以简述为分别赋予目标函数对应的权重系数，构建新的目标函数，其重难点在于寻找到较为合适的权系统，以同一尺度把多个目标函数进行统一。这里，把目标函数置于层次结构模型之中统一尺度，即有，对于多个目标函数fk（x）（其中k=1,2,3），对应目标函数的权重系数为ωk，可构建新的目标函数U（X）：

2.4 求 解

根据式（1）至式（9），结合具体的约束条件，将相关模型录入MATLAB，计算函数进行求解，求得最优解x（0）。

3 示例分析

假设在某战场区域内分散部署着4 个弹药供应点，分别为S1,S2,S3,S4，弹药总储备量为120，其中，S1=30,S2=25,S3=35,S4=30。而该区域分布着4 支任务部队提出弹药需求，（假设从弹药供应点到需求点的时间为不确定区间数），任务部队弹药需求量为区间数，其中d1=［10,23 ］，d2=［12,22 ］，d3=［13,21 ］，d4=［11,25 ］；目标概率p0=0.8。战时弹药供应过程中的cij、tij、pij，如表2 所示。

表2 战时弹药供应过程中成本、时间和道路通畅率明细

设弹药储备点到需求点的目标期望时间是1,1,2,1；则其延误时间如表3 所示。

表3 战时弹药供应过程中成本、延误时间和道路畅通概率明细

3.1 建立模型

根据表2 数据，可建立目标函数模型：

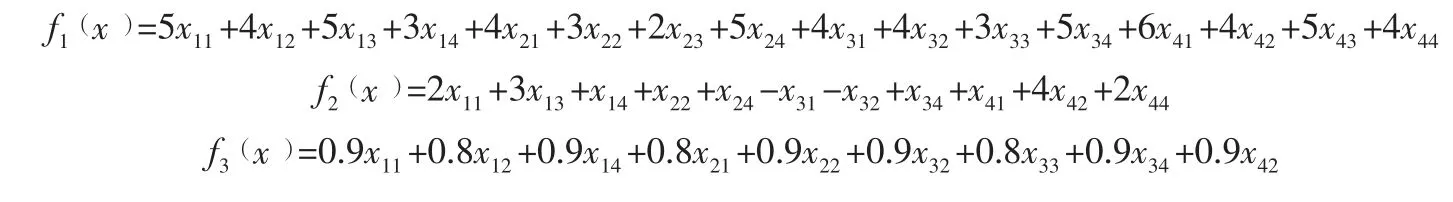
约束条件为：

3.2 确定目标函数权重系数

运用yaahp 软件，分三步求解出目标函数权重系数。

（1）建立目标函数的层次结构模型（如图2 所示）

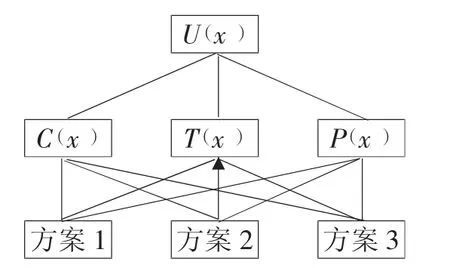
图2 目标函数层次结构模型

（2）构建判断矩阵并求解通过比较目标函数两两重要程度，按照1～9 标度法，得出如表4 所示的目标函数判断矩阵。

表4 目标函数判断矩阵

求得f1（x）权重系数为ω1=0.288 6，f2（x）的权重系数为ω2=0.402 8，f3（x）权重系数为ω3=0.308 5。

3.3 运用线性加权法，求得U（x）

根据式（10）至式（12），对目标函数统一求最小值，进行线性加权，求最优值为最小，因此在f3（x）前加负号，求得U（X）=ω1f1（x）+ω2f2（x）-ω3f3（x）。将相关数值分别代入，得：U（X）=1.95x11+0.89x12+2.65x13+0.97x14+0.89x21+0.97x22+0.58x23+1.85x24+0.75x31+0.45x32+0.6x33+1.55x34+2.13x41+2.47x42+1.44x43+1.96x44。

3.4 求 解

x11=0,x12=20,x13=0,x14=0,x21=0,x22=0,x23=17,x24=0,x31=0,x32=0,x33=0,x34=23,x41=19,x42=0,x43=0,x44=0

表5 计算结果

S1供应d220 单位弹药；S2供应d317 单位弹药；S3供应d423 单位弹药；S4供应d119 单位弹药。

4 结论

针对战时弹药调度方案决策过程中存在的复杂性、多变性等问题，以弹药调度过程为主线研究战时多目标弹药调度，结合示例，构建了以弹药调度成本最小、总延误时间最短、弹药安全运输概率最大为目标的多目标模型。基于AHP 确定目标函数权重系数，实现了定性分析向定量分析的转化，减少了人为主观性影响。运用线性加权法实现目标函数的归一化，实现了目标函数的归一化。通过yaahp、MATLAB 软件进行目标函数权重系数的计算和最优解的计算，得出弹药最佳调度方案。从结果来看，所用方法应用于战时多目标弹药调度方案决策，具有可行性和有效性，可以为指挥员正确决策提供重要借鉴。需要说明的是，本文仅考虑弹药充足的情况，而战时可能会面临弹药短缺或其它各类突发状况影响弹药调度的状况，今后可进一步结合弹药的动态分配模型探究。