考虑项目间依赖关系的项目风险应对策略选择模型
张 旭,白思俊∗,郭云涛,白礼彪
(1.西北工业大学 管理学院,陕西 西安 710072;2.长安大学 经济与管理学院,陕西 西安 710061)
0 引言
在VUCA 时代下,项目执行过程中的各类因素和事件的不确定性日益增强,因此,项目风险管理变得愈加重要。项目风险管理主要是通过识别出项目执行过程中对完成项目目标产生消极影响的不确定因素或事件,随后对其进行综合分析评价,最后采取相应的风险应对策略以减轻不确定因素或事件所带来的消极影响的过程。可见,减轻风险所带来的消极影响主要是通过风险应对策略来实现的。所以,风险应对策略的选择优化结果将直接影响项目风险管理的水平和效果。此外,项目风险管理的水平和效果将影响项目的顺利完成。因此,开展项目风险应对策略选择方法的研究具有重要意义,并且目前相关研究较少[1]。
项目风险不是相互独立,而是存在一定的关联关系,特别是基于单项目风险间的关联研究较多。例如,关欣等[2]定义了风险关联并提出了风险关联的度量方法,在综合考虑项目各目标的前提下构建了风险应对策略选择模型。张尧等[3]将风险关联分成了积极关联和消极关联,并结合Macbeth 和Dematel 方法进行度量。Fang 等[4]在考虑风险交互作用的前提下确定风险应对策略。Zhang[5]提出了一种定量衡量风险相互依赖性的方法,在此基础上,构建了风险应对策略选择优化模型。Wu 等[6]考虑了项目不同子过程之间的风险相关性,提出了新的风险应对策略选择方法。Wang等[7]利用社会网络理论建立了项目风险应对策略优选模型。但是,在实际企业管理中,项目大多数处在某一项目组合中进行管理。在项目执行过程中,与之存在依赖关系的其他项目的成功和失败都可能会对该项目风险产生一定影响。因此,现有研究忽略了项目间依赖关系对风险应对策略选择的影响。基于此,本文在考虑项目组合结构动态性和复杂性的基础上,引入项目间依赖关系对项目风险的影响,开展项目风险策略选择的研究。
项目风险应对策略的选择过程是一个决策过程,决策者的行为因素将影响最终的选择结果。因此,很多学者在进行风险应对策略选择时考虑了决策者的行为因素。例如,杨莉等[8]考虑了决策者的风险偏好,构建了以风险应对成本和风险值最小为目标的区间优化模型。Zhang 等[9]考虑了风险间依赖性和项目经理的风险厌恶行为构建了数学模型。Song 等[10]考虑了决策者行为的特点采用云模型的方法对风险决策问题进行了研究。姜艳萍等[11]考虑决策者的失望和后悔心理行为,计算各应对方案的整体感知效用值并进行排序和优选。然而,现有研究忽略了决策者会将资源或资金按照一定目的进行分类和分配[12]的客观事实。所以,为贴近决策实际,本文将心理账户理论应用到项目风险应对策略的优化选择过程中。
为了更加清晰地描述和度量项目间依赖关系和风险间关联关系,本文使用了设计结构矩阵方法(design structure matrix,DSM)。该方法于1981 年由Steward 提出,已应用到复杂系统建模、工程管理等多个领域,成为了主流的系统分析工具[13]。此外,风险应对策略选择过程中需要专家为备选应对策略对各心理账户的贡献程度进行评价。为更加充分地表达专家的偏好,获得更加详尽的描述信息,本文应用了球形模糊集(spherical fuzzy sets,SFS)以获得专家对风险应对策略的评价结果。该方法于2019 年由Gündoğdu 和Kahraman 提出,使得决策者的犹豫度可以独立于隶属度和非隶属度,较直觉模糊集等方法更贴近决策实际[14]。
综上,本文提出了考虑项目间依赖关系的项目风险应对策略选择方法。首先,本文在考虑项目组合结构动态性和复杂性的基础上,分析了项目间依赖关系对项目风险的影响,并使用DSM 方法度量了风险受项目间依赖关系的影响程度。然后,在考虑决策者的心理行为基础上,利用心理账户理论和球形模糊集,建立了以决策者效用最大化为目标,以风险应对成本符合心理账户预算为约束的项目风险应对策略选择优化模型。最后,通过算例证明了所提方法的可行性和有效性,并分析了不同程度的项目间依赖关系和心理账户对项目风险应对策略选择的影响。
1 项目间依赖关系对项目风险的影响
1.1 影响分析
随着规模的不断扩大,企业需要越来越多的项目来满足战略需要。所以,绝大多数项目在企业环境内并不是独立存在的,而是与其他项目以优化战略资源为核心[15]进行组合,即项目组合。但是,目前的相关研究通常把项目视为封闭系统,仅考虑该项目内风险之间、工序之间的关联性,而忽略了项目组合中存在依赖关系的其他项目的执行情况对该项目风险的影响。
在项目组合中,项目之间会存在一定的依赖关系[16]。本文在现有研究的基础上,将项目之间的依赖关系按照依赖类型分为技术依赖、资源依赖、收益依赖和知识/经验依赖[17];按照作用对象将项目间的依赖关系分为直接依赖关系和间接依赖关系。图 1(a)实线箭头表示为项目P2依赖于项目P1,同理(b)为项目P2与项目P1相互依赖。图1(c)中项目P3与项目P2和项目P2与项目P1为直接依赖关系。项目P3与项目P1虽无直接依赖关系,但由于项目P3、P1均与项目P2存在依赖关系,所以项目P3与项目P1之间为间接依赖关系。

图1 依赖关系和输入关系介绍Figure 1 The project interdependencies and input relationships
其次,图1 中所示的虚线箭头表示被依赖项目对依赖项目产生的影响。以图1(a)为例,项目P2依赖于项目P1,所以,项目P1的成功或失败会对项目P2产生一定影响。这种影响可看作项目P2的外部输入,即一个项目的成功或失败都可能对依赖于它的项目产生影响[18]。所以,在进行项目风险应对策略选择时,不仅要关注该项目的风险状况,也需要关注所依赖的其他项目的成功或失败的概率[18-19]。以图2 为例。项目P0为目标项目,即为该项目选择风险应对策略,P1-4为其他项目。项目P0与P1-4存在不同的依赖关系。假设项目P0直接技术依赖于项目P2,当项目P2结束时,若成功,则技术转移较为顺利,项目P0的技术相关风险可能会得到一定的减轻;若失败,可能因技术转移难度加大而增加项目P0技术相关风险。因项目P0与其他项目之间的关系较项目P0与P2关系相似,所以在此不予赘述。除此之外,风险之间也存在一定的关联关系。关联关系可将项目P1-4所带来的影响在项目P0内风险之间进行扩大或缩小的传播[3],如图 2 所示。因此,项目间依赖关系对项目风险具有重要影响,也为选择合理的风险应对策略加大了难度。
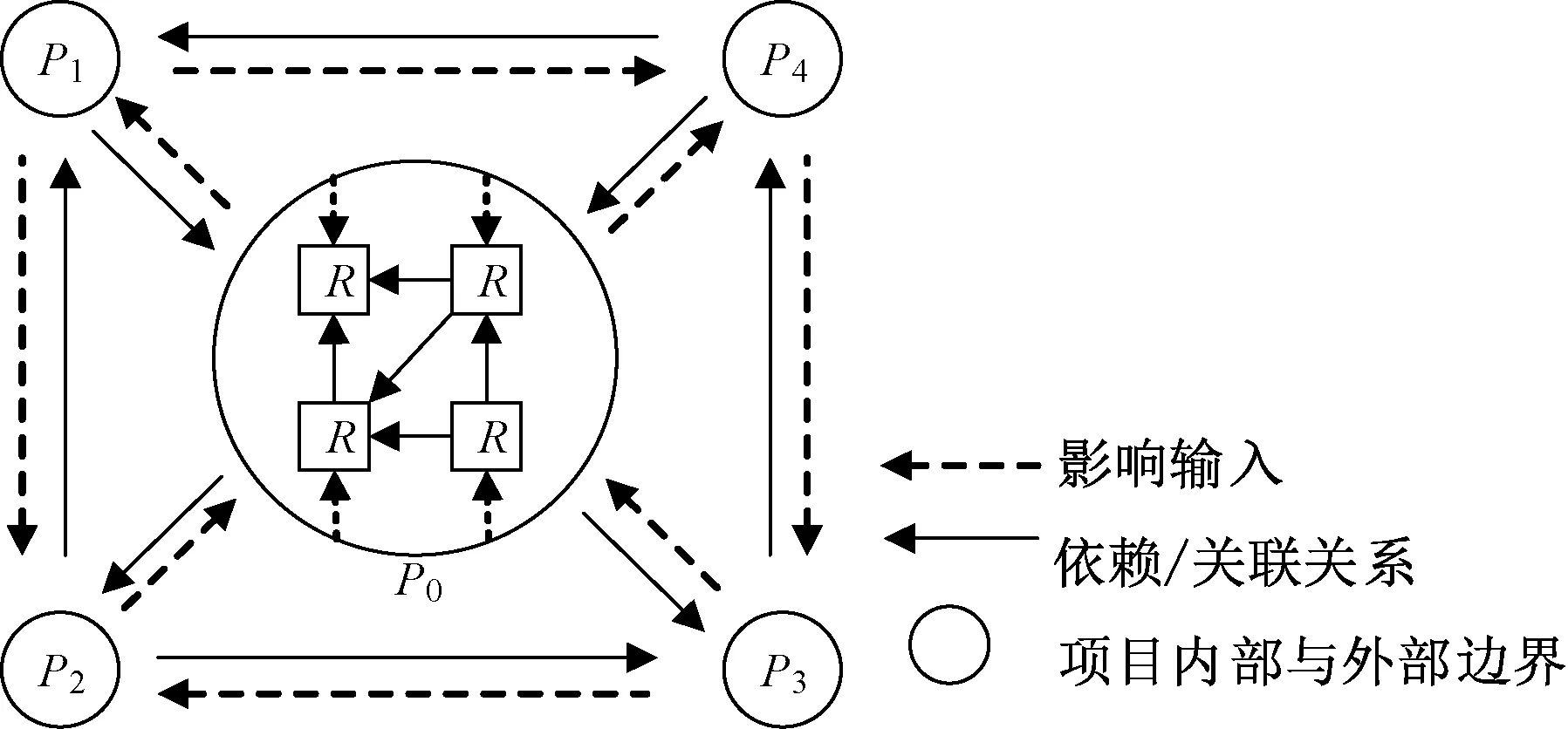
图2 项目依赖关系对项目风险影响分析Figure 2 The analysis of the impact of project interdependencies on project risks
此外,项目组合结构的动态性和复杂性[18]同样对项目风险有重要影响。动态性是在目标项目的生命周期内,其依赖的项目可能会结束,同时也会有新的且存在依赖关系的项目加入。假设t时刻项目组合结构如图3(a)所示,至(b)t+1 时刻,项目P2结束了,新增了项目P6。对于目标项目P0来说,项目之间的依赖关系发生了变化。项目组合动态性、项目间复杂的依赖关系以及影响输入的存在使得项目组合的结构具有复杂性。如图3 所示,由于项目P6的加入,项目P6与项目P5间的依赖关系由项目P5直接依赖于项目P0,转变为项目P5直接依赖于项目P0且项目P6间接依赖于项目P0。易知,影响输入关系也随之发生了变化。所以,项目组合结构的动态性和复杂性加大了项目风险的不确定性,也为选择出合适的风险应对策略加大了难度。这需要决策者以多阶段、动态的视角去考虑项目间的依赖关系对项目风险的影响,从而使决策结果更加真实有效。

图3 项目组合结构动态性和复杂性Figure 3 The dynamics and complexity of portfolio structure
1.2 影响强度度量
项目间依赖关系对项目风险的影响在复杂、动态的项目组合结构下显得尤为重要且复杂。找到较为合适且便捷的方法度量此影响是很有必要的。在目前研究的基础上,本文利用式(1)(2)对项目P0的风险Rj在P0的生命周期中受存在依赖关系的其他项目的影响强度进行度量。
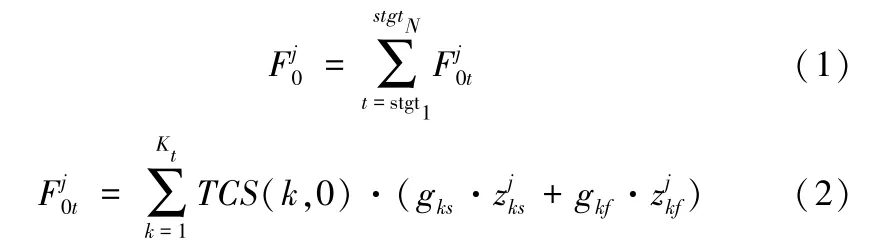
由图2 和图3 可知,项目间的依赖关系是一个复杂的网络。节点为项目,项目与项目之间通过箭线连接即项目间的依赖关系,其强度可按照依赖数量来确定[17,20]。假设各依赖关系无重要程度区分,依赖所造成的影响强度可进行叠加。则可将图4(a)项目间依赖关系图利用DSM 表示,如图 4(b)所示。DSM 中“列”表示项目依赖于其他项目的强度,“行”表示项目被其他项目依赖的强度。例如项目P0依赖于项目P3、P4强度分别为3 和4。P0被P5依赖强度为3。

图4 项目间依赖关系网络和DSM 表示Figure 4 Project interdependencies network and the representation with design structure matrix
本文将依赖关系分为直接依赖和间接依赖,所以项目间的连接总强度(Total Connection Strength,TCS)可由直接连接强度(Direct Connection Strength,DCS)和间接连接强度(Indirect Connection Strength,IDCS)组成。直接连接强度指的是项目间存在直接依赖关系的连接强度。间接连接强度指的是项目间为间接依赖关系的连接强度。两者计算公式[13]如式(3)、(4)所示。

式(3)中,DCS(k,0)表示项目P0对项目Pk的依赖关系强度,K为除目标项目外的项目数量。

式(4)中,项目Pm为项目Pk和项目P0的邻接节点,K1为项目P0到项目Pk的所有邻接节点的数量。INk为项目Pk入度直接连接强度,INk=,K2为指向项目Pk的项目节点个数;OU0为项目P0出度直接连接强度,OU0=,K3为项目P0指向的项目节点个数[17]。综上,项目Pk和项目P0的连接总强度TCS(k,0)如式(5)所示。

2 项目风险应对策略选择优化模型
2.1 模型构建
通过分析项目间依赖关系对项目风险的影响,可知项目间依赖关系对项目风险有重要影响。所以,在为项目选择风险应对策略时,需要考虑项目间的依赖关系。已识别出项目风险集R={R1,R2,…,RJ},Rj表示第j个风险,j=1,2,…,J。备选的应对策略集为A={A1,A2,…,AI},Ai表示第i个风险应对策略,i=1,2,…,I。因此,构建项目风险应对策略选择优化模型如下。

其中,式(6)为目标函数,以决策者效用最大化为目标,Wj为风险Rj的权重,U(xij)为效用函数。式(7)为质量心理账户(MAQ)约束条件,Ci为风险应对策略Ai的应对成本,max(xij)保证当Ai应对多个风险时,Ai的成本仅计算一次,diQ为风险应对策略Ai属于质量心理账户(MAQ)的隶属度,βQ为质量心理账户(MAQ)所能分配的资金占比,B为风险应对预算。同理,式(8)、(9)中diC、diT分别为风险应对策略Ai属于成本心理账户(MAC)和进度心理账户(MAT)的隶属度,βC、βT分别为成本、进度心理账户所能分配的资金占比。式(10)为0-1 变量参数,当为1 时,选择风险应对策略Ai应对风险Rj,当为0 时,则不选择。下面将对效用函数,心理账户隶属度和心理账户所能分配资金占比进行详细描述。
2.2 效用函数
在实际决策中,决策者并非完全理性的,而是有限理性的。所以,以效用最大化作为优化目标使其更加贴近决策实际。由于绝大多数的决策者在进行决策时都是厌恶风险的,所以采用式(11)测度决策者的效用值[3]。
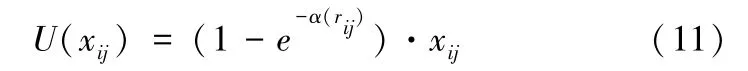
其中,α为决策者的风险厌恶程度,一般取应对预算的1/6 的倒数[3,5,21]。rij为风险应对策略Ai应对风险Rj的期望效果。
2.3 权重函数
在项目风险应对策略选择过程中,Wj反映了风险Rj所造成消极影响的严重程度。本文Wj主要由三部分构成,分别为项目间依赖对风险Rj的影响程度Fj,风险Rj的风险间关联强度Hj和期望损失Bj。所以,Wj可由式(12) 求得。

其中,λ1,λ2,λ3分别为Fj,Hj,Bj所占比重。风险间关联强度的量化与项目间依赖关系相同。关联关系由0 或1 表示。为1 时两风险间存在关联关系,为0 时两风险间不存在关联作用。然后,可建立风险关联DSM。最后,利用式(3)至(5)计算风险Rj的关联强度Hj。
2.4 约束条件
模型的约束条件主要应用了心理账户理论。心理账户理论由芝加哥大学教授Richard Thaler[22]于1980 年提出,是决策者对选择结果进行分类、记账、编码、估价和预算的过程[23]。心理账户理论中描述心理账户的主要特征为非替代性,即不同心理账户内可利用的资源是不能相互替代的。基于此特征,本文将决策者的心理账户按照项目的基本目标,分为质量心理账户(MAQ)、成本心理账户(MAC)和进度心理账户(MAT)。各心理账户所能支配的资金占应对预算的比例分别为βQ、βC、βT。其占比可由决策者根据经验知识、风险偏好和项目特点确定。
然后,需要计算风险应对策略对各心理账户的隶属度,以明确如何分担风险应对策略成本。为更加充分表达专家的偏好,获其更加详尽的描述信息,本文应用球形模糊集(spherical fuzzy sets,SFS)以确定风险应对策略对各心理账户的隶属度[14]。
首先,邀请M 名相关领域专家。根据经验和知识储备确定专家m所占权重为ωm,m=1,2,…,M。按表 1 所示,对风险应对策略Ai对MAQ,MAC,MAT 的贡献度进行打分,分别记为。表1 中,μ为隶属度,v为非隶属度,π为犹豫度。

表1 语言评价集和球形模糊数Table 1 Language evaluation sets and spherical fuzzy numbers
对贡献程度打分结束后,按照式(13)利用球形算数平均权重(spherical weighted arithmetic mean,SWAM)确定专家决策球形模糊数[14]。以为例。
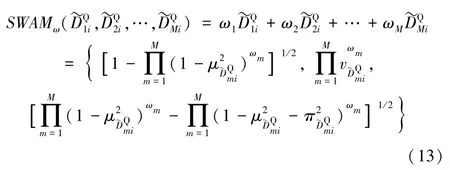
然后按照式(14)得到风险应对策略Ai对心理账户MAQ的原始贡献值[14]。

由式(14)计算出来的贡献值有正有负。为保证所得贡献值非负,本文首先将表1 中的评分标准通过式(13)(14)计算得到原始贡献值,发现最小值为-0.64,最大值为0.64。然后,根据表1 中的评分标准数量,对原始贡献值区间进行调整,设定最小值为0,最大值为8。可知,原始贡献值区间长度为1.28,调整后的区间长度为8,所以调整后贡献值区间长度是原始区间长度的6.25 倍。因此,为保证调整后贡献值非负且与原始贡献值相匹配,可通过式(15)计算得到调整后贡献值。
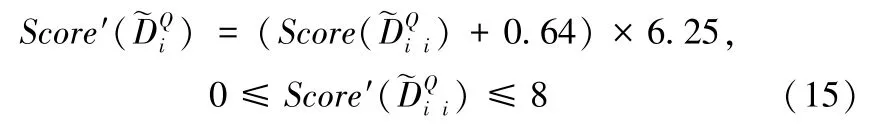
最后,根据风险应对策略Ai对心理账户MAQ 的贡献值进行归一化,如式(16)所示。同理,风险应对策略Ai对心理账户MAC 和MAT 的贡献值可通过式(17)和(18)进行归一化。

3 算例分析
3.1 算例描述
本文以A 公司为例,其所拥有的项目基本情况如表2 所示。项目P0的管理团队已经完成了对项目的风险以及风险应对策略的识别和评价工作。具体信息如表3 和表4 所示。项目P0的项目经理以年为单位将项目分为4 个时间段,以各时间段初期为参考点度量项目间依赖关系对项目P0的风险的影响,选择风险应对策略。
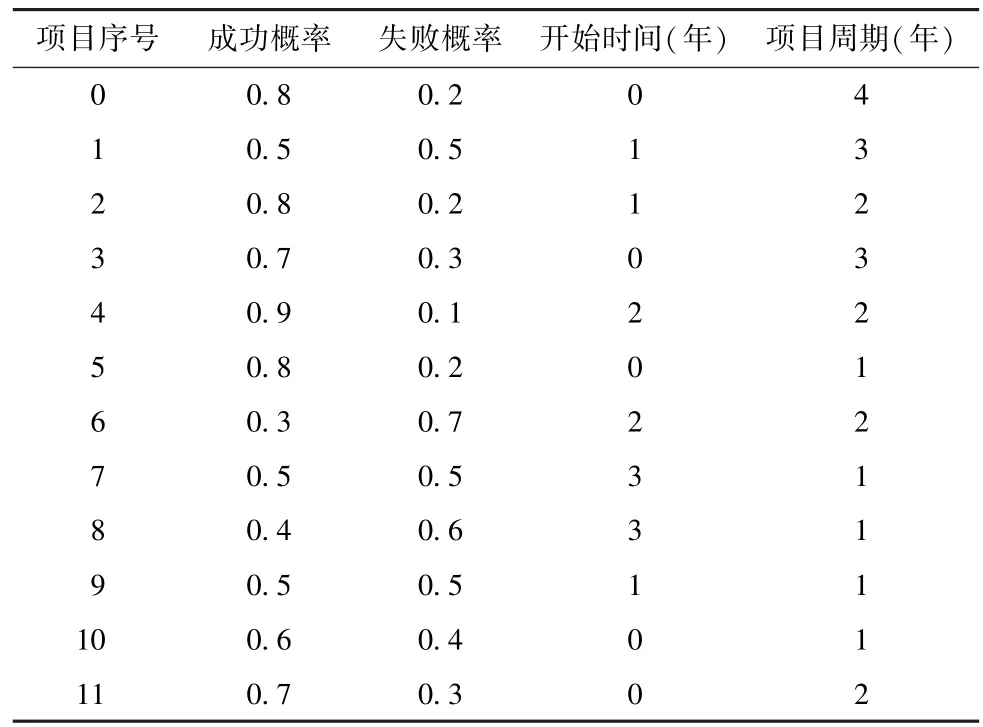
表2 各项目的基本情况Table 2 Basic information of each project

表3 项目风险以及预期损失Table 3 Project risks and expected losses

表4 风险应对策略与实施效果Table 4 Risk response strategies and implementation effect
3.2 算例计算
结合项目情况,专家给出了其他项目对P0风险的影响、项目间依赖强度关系DSM 和风险间关联关系DSM,并根据式(1)至(5)计算出项目间的影响强度以及风险间的关联强度如图5、图6 和表5 所示。

表5 项目间依赖对风险的影响强度和风险关联强度Table 5 The impact of project interdependencies on risks and the correlation strength between risks

图5 其他项目对项目0 风险的影响Figure 5 The impact of other projects on risks of project 0
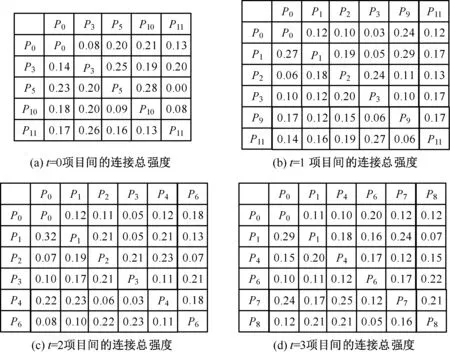
图6 各阶段项目间的总连接强度Figure 6 Total connection strength between projects in each phase
随后,邀请3 名专家对各风险应对策略对各心理账户的贡献程度进行评测。专家评分所占权重值分别为ω1=0.5,ω2=0.2,ω3=0.3。专家1 评分结果如表6 所示,其余专家省略。

表6 专家1 评分结果Table 6 The evaluation result of the first expert
然后,根据式(13)至(18)计算求得各风险应对策略对各心理账户的隶属度如表7 所示。

表7 各风险应对策略对各心理账户隶属度Table 7 The degree to which risk response strategies belongs to mental accounts
3.3 结果分析
将上述的评价结果及相关数据带入构建的项目风险应对策略优化选择模型中,设定βQ=0.4、βC=0.3、βT=0.3。然后使用Gurobi 进行求解。为了研究项目间依赖关系对项目风险应对策略选择的影响,本文计算了不同λ1值和风险应对预算下的最优风险应对策略集。具体如图7 和表 8 所示。
由图7 和表8 可知,

表8 不同预算及 λ1 下的最优项目风险应对策略集Table 8 Project risk response strategy sets under different budgets and λ1

图7 不同预算及λ1 下的决策者的效用值Figure 7 The decision maker′s utility under different budgets and λ1
(1)在应对预算一定的情况下,决策者的效用值随λ1值的增大而提升。当λ1=0 时,决策者的效果值最小;当λ1=1 时,决策者的效用值最大。所以,在决策者选择风险应对策略时,考虑项目间依赖关系是十分重要的。
(2)在λ1一定的情况下,决策者的效用值随应对预算的增加,先增加后减小。这与张尧等[3]结论相似。所以,存在最优的应对预算使得决策者效用最大。因此,在选择风险应对策略时,应对预算并不是越多越好。
(3)在λ1一定的情况下,随着应对预算的增加,决策者效用值增加速度较为缓慢,当效用值到达最高点后,决策者的效用值降低速度较为急促。这说明单位资金下给决策者带来的正效用低于单位资金下给决策者带来的负效用。因此,在增加应对预算时决策者要慎重,很有可能效用值快速下降。
(4)由表4 可知,当应对预算接近可供执行全部应对策略时,决策者并没有全部选择风险应对方案且效用值为各应对预算下的最低值。
(5)当应对预算低于最优应对预算时,λ1的取值对项目风险应对方案的选择存在影响。λ1的取值越高,风险应对策略集可应对的风险数量越多,以保证降低项目的整体风险,提高决策者效用。例如,当应对预算为1000 万元时,随着λ1的值增加,A13替换了A21,A21可以应对2 个风险,而A13可以应对3 个风险。
(6)当应对预算大于最优应对预算时,λ1的取值对项目风险应对策略选择没有影响,但是对决策者的效用值产生了影响。
此外,为了分析心理账户对项目风险应对策略选择的影响,本文计算了考虑心理账户和不考虑心理账户的项目风险应对策略选择集。通过分析得出表9 所示结果。

表9 考虑和不考虑心理账户下投入每千元时决策者所获取的效用差值Table 9 The comparison between utility values considering MA and utility values not considering MA
由表9 可知,各值均大于零。所以,考虑心理账户时每千元的决策者效用值在各种情况下均高于不考虑心理账户时的效用值。这说明考虑心理账户时,资金利用效果更好,能更具针对性地满足决策者的心理需求。不考虑心理账户时,仅以效用值最大化为目标,资金利用效果相对下降,导致单位资金下决策者的效用值较小。因此,在进行项目风险应对策略选择的过程中,应考虑决策者的心理账户对应对策略选择结果的影响,使得决策结果更贴近实际,资金利用效果更高。
4 结论
随着规模的扩大,企业管理的项目越来越多,因此,项目大多数处在某一项目组合中进行管理。所以,项目在进行风险应对决策时需要考虑其他项目对决策的影响。首先,本文在考虑项目组合结构动态性和复杂性的基础上,分析了项目间依赖关系对项目风险的影响并利用DSM 方法进行了度量。然后,利用心理账户理论和球形模糊数构建了项目风险应对策略选择优化模型。最后,通过算例分析证明了所提方法的可行性和有效性,并分析了不同项目间依赖作用以及心理账户对项目风险应对策略选择的影响。通过研究得出了以下结论:
(1)项目间依赖关系会影响项目风险应对策略选择结果。所以,在实际决策中,决策者需要考虑项目间依赖关系对项目风险的影响。
(2)在项目间依赖关系占比一定的情况下,决策者的效用值随应对预算的增加,先增加后减小,即存在最优的应对预算使得决策者的效用值最大;当应对预算低于最优值时,随项目间依赖作用的增加,决策者更加倾向选择能够应对更多风险的策略;当应对预算大于最优应对预算时,项目间依赖关系不影响项目风险应对策略选择结果,但影响决策者的效用值。
(3)决策者效用值增加的速度小于减小的速度。当应对预算大于最优值时,决策者可能会较快地感受到效用值的降低;随着应对预算的增加,决策者的效用值可能低于应对预算较低时的效用值。
(4)考虑心理账户时,决策者的单位投入资金的效用值在任何情况下均高于不考虑心理账户时单位资金投入的效用值。这说明考虑心理账户理论提高了资金的利用效果,使得决策结果更加贴近实际。
本文首次将项目间依赖关系和心理账户理论引入到项目的风险应对策略选择的研究中。所得到的结论不仅为今后的相关研究提供了理论基础,也为实际决策提供了决策支持。在今后的研究中,可以关注项目决策者的其他心理行为对决策结果的影响,也可以研究不同时刻的影响强度间的关联关系。

