基于变分模态分解与注意力机制的海洋风速预测

章 靖 凯， 顾 宏， 秦 攀， 余 向 军

( 1.大连理工大学 控制科学与工程学院，辽宁 大连 116024；2.海军大连舰艇学院 军事海洋与测绘系，辽宁 大连 116018 )

0 引 言

在远洋航行领域，准确的风速预测结合海况信息预报，可以为船舶航行设计出最佳的航线[1]，在保障航行安全性的同时，减少航时与油耗．在军事领域，气象状况是一项极为重要的参考因素，借助准确的气象预测，军事指挥人员可针对性装配部队，制订行军方案，从而提高军事行动成功率．军事需求在很大程度上直接推动着天气预测技术的发展[2]．

传统气象数值预测技术中采用WRF[3-4]等NWP数值天气预报物理模型，对实时气象运行规律有较好的模拟，但建模过程本身的复杂性与对环境信息精确性的高依赖度，使得结果表现出对短期高精度预测的不确定性[5-6]．区别于经典物理模型基于气象变化机理的解析，新兴的气象预测技术主要从统计机器学习方向展开对气象时间序列数据的处理．基于模糊聚类法[7]等分类方法可对时间序列数据进行分类，并以之所属类型结合自回归移动平均法[8]、自回归差分移动平均法[9]、卡尔曼滤波[10]等经典计量模型进行短时预测．然而，基于经典计量模型的风速时序预测方法往往建立在严格的假设之上，预测精度易受到时间序列随机波动性、不稳定性等因素的限制，采用支持向量机[11-12]、人工神经网络[13]等基于数据驱动的模型可有效提高精度，增强模型泛化性．在深度学习领域，李大中等[14]提出了一种基于卷积循环神经网络的深度学习模型，较一般机器学习算法在短期预报精度上有较大的提高，但在长距离预测中表现不佳．Shi等[15]提出了一种卷积长短期记忆神经网络，并在多普勒雷达回波时间序列数据上进行验证，取得了较传统物理模型光流法更好的预测结果．此外，一些研究开始注重在数据预处理阶段就对原始数据进行降噪、降低复杂度等处理，采用“分解-预测-重构”的思路．田中大等[16]提出了一种基于小波变换的风速组合预测模型．Santhosh等[17]采用集成经验模态分解算法对原始数据进行分解，并将解构之后的信号输入神经网络进行模型参数训练，对时序数据的预测精度有较大提升．然而，分解算法在一定程度上会引起端点效应、模态混叠现象，干扰实际预测效果．

针对以上问题，本文提出一种基于变分模态分解与融合注意力机制的神经网络模型进行风速预测．变分模态分解[18-19]可有效提高噪声鲁棒性，使得风速时间序列得到有效特征分解．基于Transformer[20]的融合注意力机制的神经网络模型具有抓取全局内部关联信息的能力，可有效捕捉长距离依赖关系，提升模型长距离预测性能．首先，通过变分模态分解对原始信号进行降噪与特征提取；然后，将处理后的信号输入融合注意力机制的神经网络进行风速预测；最后，利用浮标站实测数据进行验证，并与其他方法进行比较．

1 方 法

1.1 整体流程

1.2 数据预处理

选取美国国家海洋和大气管理局数据浮标中心观测数据作为数据集．因浮标设备问题，有时会出现测绘数据丢失的情况，若不加修正将削弱模型的拟合与泛化能力，故本文采用一种分权线性插值算法，将更大的权重分配给更靠近缺失点或异常点处的可用值，用以填充原始浮标数据中的缺失值．同时，为消除数据集中特征变量量纲不同对实验造成的影响，本文采用均值方差归一化方法将数据缩放至同一尺度(均值为0，方差为1)，并分别应用于训练集、验证集与测试集．

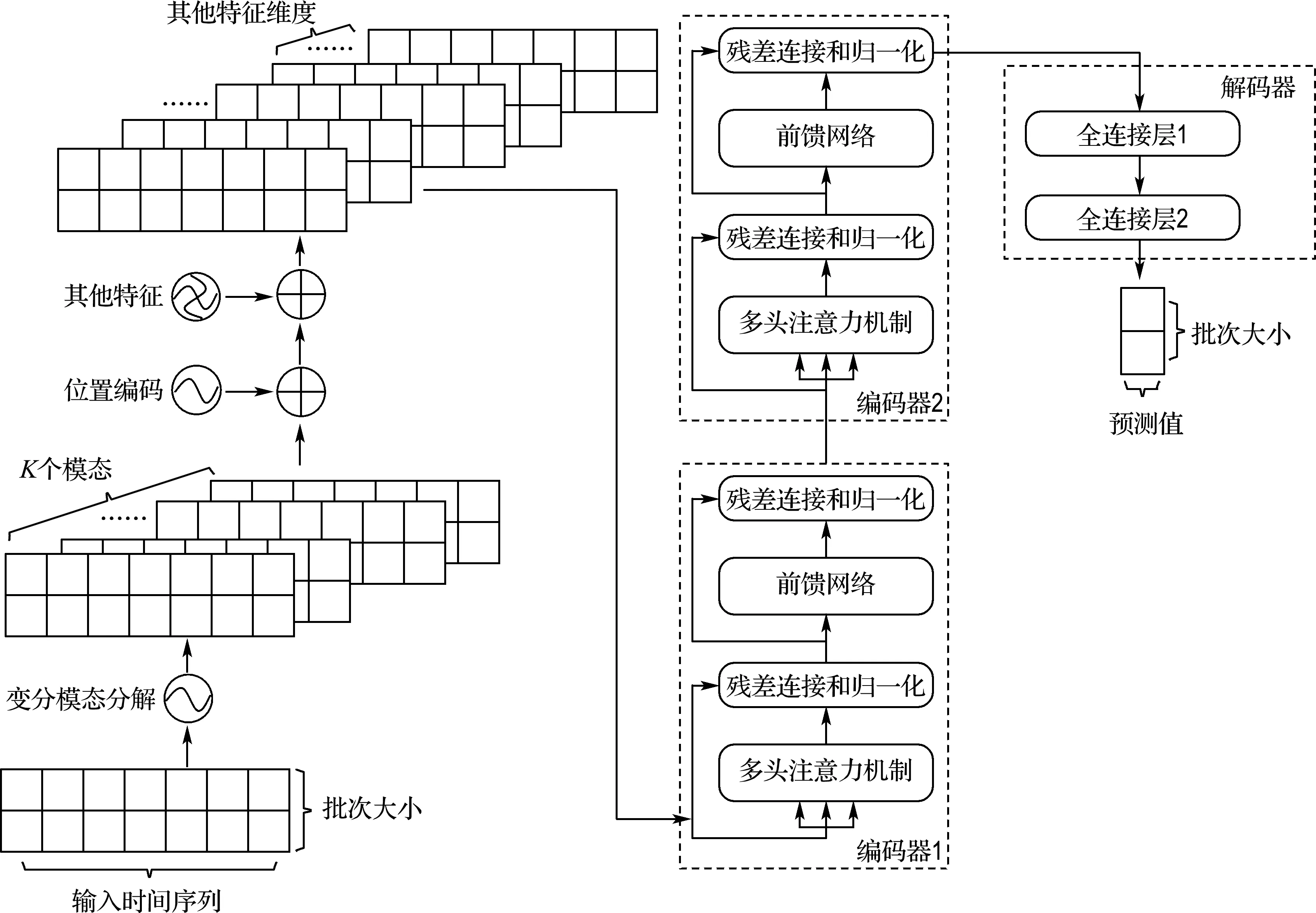
图1 VMD-Transformer模型整体流程

1.3 变分模态分解

对预处理后的时序数据做变分模态分解[21]，以某一相关变量时序u(t)为例，将其分解为K个具有特定模态的序列uk(t)，k=1，2，…，K，满足K个模态重构之和等于序列u(t)的条件下，各模态的估计带宽之和最小．构造非约束性变分问题：

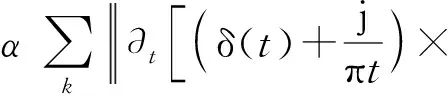
(1)

其中δ(t)为狄拉克函数，wk为第k个模态的中心频率，α作为二次惩罚因子可保证时间序列在混入噪声信号的情况下的重构精度，λ(t)作为拉格朗日乘法算子以保持约束条件严格性．采用交替方向乘子法可求得各模态新分量：

(2)

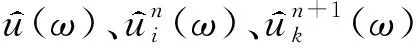
对选取的J个变量输入序列均做变分模态分解，各分解为K个模态，特征变量维度变为J×K，输入矩阵变为U′∈RL×(J×K)．

1.4 融合注意力机制的神经网络

基于Transformer的融合注意力机制的神经网络与经典的递归神经网络LSTM、RNN相比，完全基于注意力机制，无须递归与卷积计算，使其在模型参数计算上不再依赖于由前一位置的输出与当前位置的输入来计算得到当前位置的输出，从而将串行化计算转换为并行化计算，有效节省运行时长．并且，传统的递归神经网络提取全局信息能力较差，在长时间尺度特征提取与预测上有较大瓶颈．Transformer可从全局提取信息，在长时间尺度特征提取与预测上有较大优势．

如图1所示，模型分为编码器与解码器两部分．其中，编码器由若干相同的单元块组成，每个单元块又由两个子单元组成，包括多头注意力机制层和前馈网络层，每一子层都增加残差连接和归一化．本文采用双层全连接神经网络作为解码器．

经变分模态分解后的时序数据，首先会进行位置编码．相较于RNN、LSTM等递归神经网络和CNN等卷积神经网络可以获取数据相对位置信息的特征，Transformer无法获得输入信息的空间关系，因此为了利用时间序列的位置信息，在模型中引入位置编码以记录序列中各数据间相对位置信息．Transformer为每个输入序列配置特有位置向量，向量遵循特定模式，有助于确定序列中不同单点数据的位置信息与相互关系，使得后续计算中能更好地表达各数据点的相对信息．

位置编码采取方法如下：构造与输入数据维数一致的矩阵P∈RL×(J×K)，通过式(3)确定矩阵值，与输入矩阵相加得到注意力层输入U″∈RL×(J×K)．

(3)

其中，p∈[1,L]表示该单点数据在整个序列中的相对位置顺序，dm=J×K，i∈[1,L]表示变量维度序号．整个输入序列信号可以注入一定的位置信息，位置信息的差异取决于频率和相位的差异．

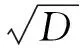
(4)

式(4)右侧即为Q与K各元素的相关程度或匹配程度，A∈RL×D．

多头注意力机制(图2)通过h个不同注意力层进行线性变换可投影多组不同的K、Q、V，即模型中存在多个子空间，将自注意力机制应用于每个子空间，最后将不同子空间注意力层输出进行拼接可得到多层注意力机制层输出矩阵M=(A1A2…Ah)∈RL×(h×D)，将其做线性变换以转换成与注意力层输入矩阵U″相同维度输出结果．上述这种通过增加多头注意力的机制，进一步完善了注意力层，可扩展模型专注于不同位置的能力．

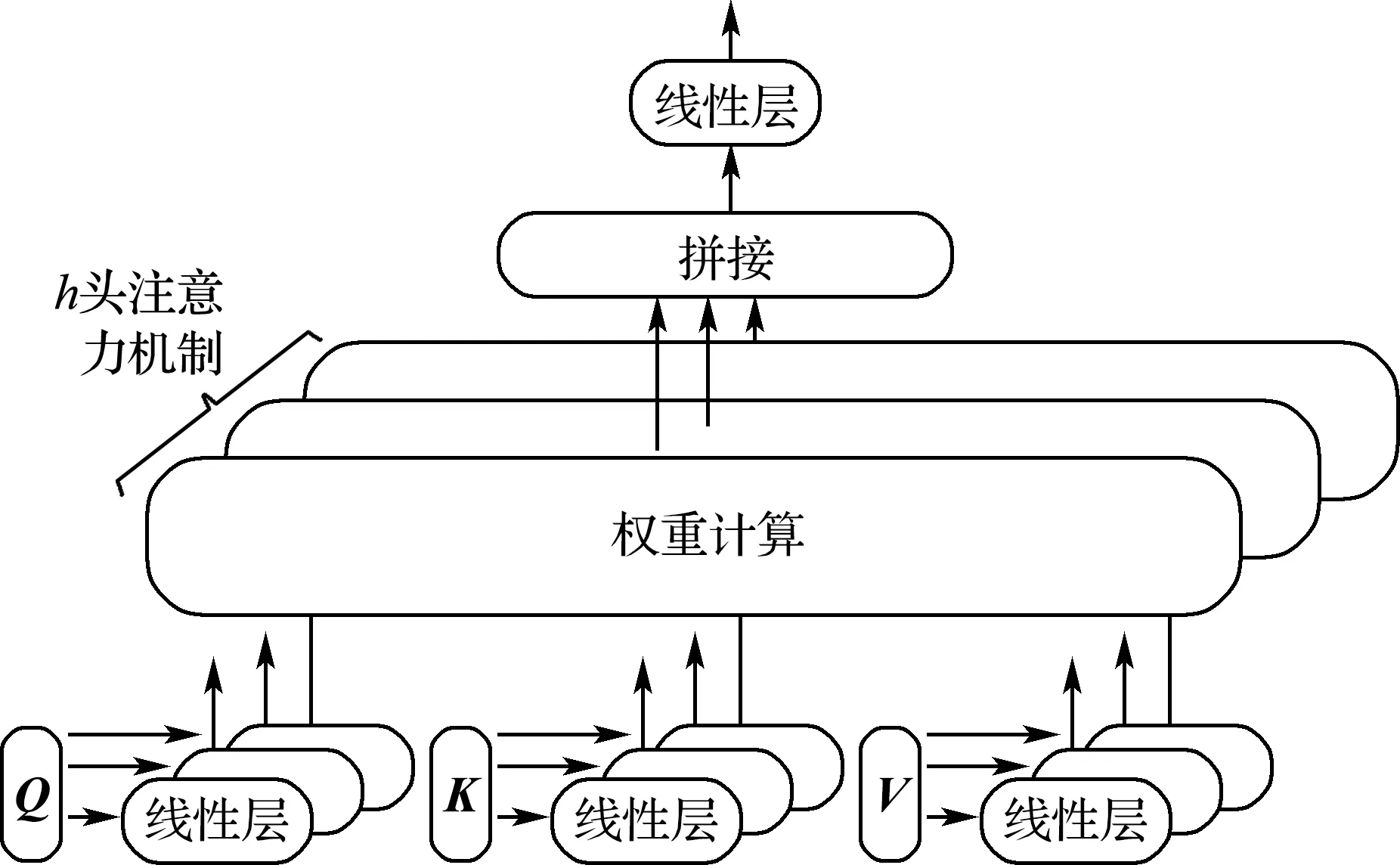
图2 多头注意力机制

编码器中的每一单元都包含一个全连接的前馈网络，其输出可表示为

N=ReLU[(XW1+b1)W2+b2]

(5)

式中：X∈RL×(J×K)是前一层的输出；W1，W2∈R(J×K)×(J×K)是权重矩阵；b1，b2∈RL×(J×K)是偏移值．

注意力层或前向反馈层输出经归一化后与该层的输入相加做残差连接，以避免深层神经网络性能退化．然后将编码器处理后的时序数据输入解码器即双层全连接神经网络以得到模型的预测结果．

1.5 模型参数设置

变分模态分解所涉及的超参数有目标模态数K、惩罚因子α、保真度稀疏τ和收敛停止条件．根据经验值分别取α=1 000，τ=1×10-6，=1×10-9．目标模态数的设定取决于各模态中心频率有无重叠且最后一层分量的中心频率是否保持相对稳定，若K取值过大，则会导致模态重叠并引入噪声，若K取值过小，则会存在分解不彻底问题，影响预测精度．实验观察发现，当K=8时，最后一层分量保持相对稳定，达到较理想的分解结果．以风速连续36个观测采样值经归一化后作为量纲一输入序列经变分模态分解为例，如图3所示．

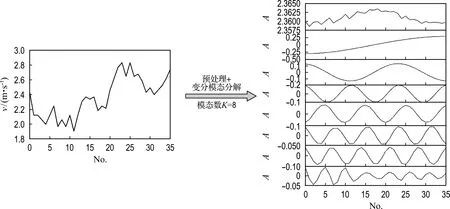
图3 变分模态分解示例图

设定编码层为2，其中多头注意力机制层设定为双头注意力，解码器为双层全连接神经网络，隐藏单元分别为36和18．网络以均方误差作为损失函数，利用反向传播算法更新网络参数，使用自适应优化器Adam对网络模型参数进行优化．模型正则化Dropout比率设定为0.2．Adam优化器学习率设定为0.002．

2 实 验

2.1 数据来源

实验数据集选自美国国家海洋和大气管理局数据浮标中心(https：//www.ndbc.noaa.gov)．本文选取48.493°N、124.726°W的浮标站46087于2015-12-31～2020-11-23所测以30 min为时间间隔的气象数据共84 944条作为数据集．将站点所测风向、风速、阵风、大气压力、气温与水温等作为6个可能影响风速预测的特征变量，以连续观测18 h共36个观测值组成输入数据U∈RL×J，其中L=36，J=6．

本文选取浮标观测数据作为影响风速预测的自然因素组成输入数据，分别以未来1、2、3、6、12、18步的风速作为输出标签，并且将数据集按85%、10%与5%的比例划分为训练集、验证集与测试集．

2.2 评价指标

本文对风速进行一步至多步预测，选取均方误差E与决定系数R2作为预测结果准确度评价指标．性能指标的定义如下：

(6)

(7)

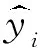
2.3 实验结果与分析

为验证模型有效性，将本文模型与LSTM、VMD-LSTM、Persistence Model等其他经典模型进行风速预测性能对比．将模型在训练集上进行训练，每训练一轮便在验证集上进行验证并比较验证效果，当模型在验证集上的性能连续5轮不再改善时，停止训练，将验证效果最好的一次模型参数保存并用于风速序列预测．因预测步长超过18步后预测误差较大，故本文仅选取18步内预测进行对比实验，结果如表1、2所示．

表1、2各项指标数值后括号内数据为该预测步长下最优模型相对本模型性能指标提升比例．

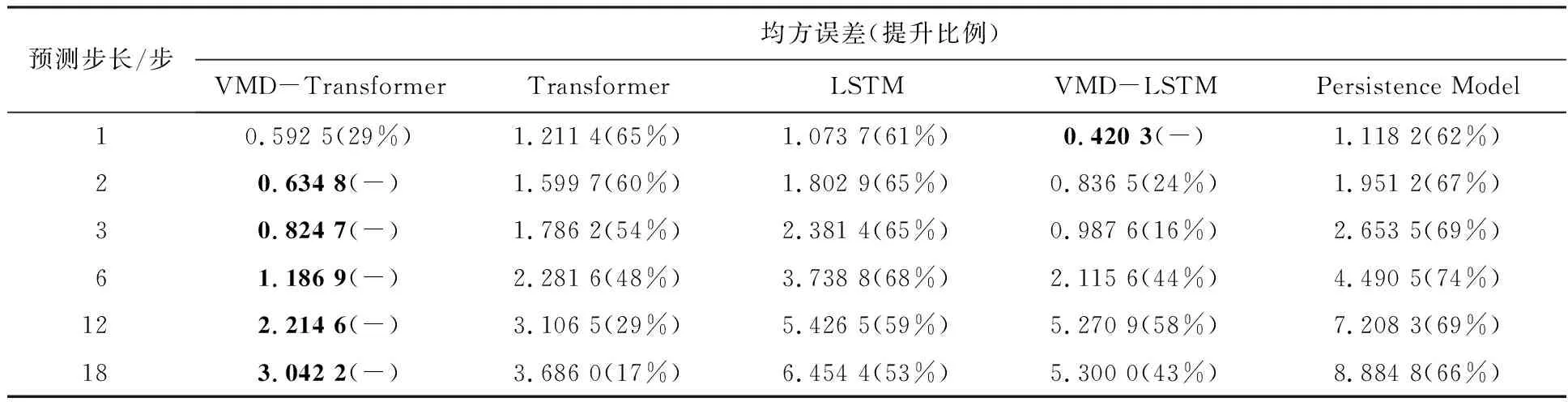
表1 模型预测效果对比(均方误差)

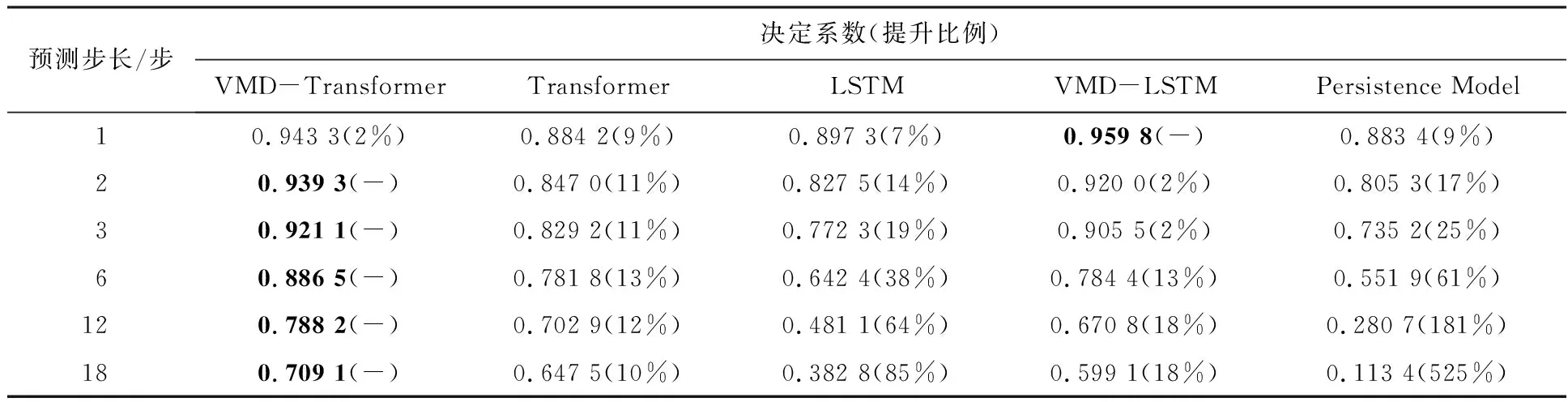
表2 模型预测效果对比(决定系数)

由表可知，随着预测步长的增加，模型的预测结果显著偏离实际值，多步预测性能逐渐不佳．通过比对实验结果可发现，相比于未经变分模态分解直接对原始数据进行处理，结合VMD的模型都具有更佳的预测表现，表明VMD可有效提取输入时间序列数据的特征，为模型提供更易感知的序列特征，使模型预测效果更优异．同时，对比不同神经网络模型，发现VMD-LSTM在1步预测上效果较优，但VMD-Transformer在2～18步等多步预测上各项指标更优异，具有与实际观测值更小的偏离程度，在实验预测步长范围内展现出更好的长序列预测敏感性与更优的多步预测性能，故可知引入融合注意力机制的神经网络Transformer与循环神经网络LSTM相比，对全局信息特征的学习效果更佳，从而使其在一定范围内相对更长时间序列的预测中有更佳优良的表现．

3 结 论

(1)变分模态分解根据其自适应时频分解特性，在滤除噪声、降低数据复杂度的同时，可将原始信号分解为具有不同中心频率的若干特征序列，提高噪声鲁棒性，为神经网络模型提供更易感知的特征信息，使后续模型预测性能显著提升．

(2)基于Transformer的融合注意力机制的神经网络利用其多头注意力机制，可在序列的不同子空间学习相关位置信息，提升序列长距离依赖的敏感度，从而使其在抓取时间序列全局信息上有着较传统循环神经网络更好的性能，在2～18步等多步长风速预测上表现出优异预测效果．

(3)实验表明，本文所提基于变分模态分解与融合注意力机制的神经网络模型可有效提高风速时序预测准确度，具有一定实际应用价值，可为研究者进一步研究时序预测提供参考思路．