考虑流线干扰的轨道交通车站应急疏散仿真

卢子琳，李洋洋

(重庆交通大学 交通运输学院，重庆 400074)

针对当前城市交通流量急速上升、交通拥堵不断加剧的局面，大力发展轨道交通，同时与高铁、公共汽车及轮渡等交通工具有机结合，已成为城市发展的必然趋势。轨道交通由于具有耗能低、污染少、客流运送量大的特点在城市交通系统中发挥重要作用，城市轨道交通也因此迎来了新的发展机遇。据中国城市轨道交通协会2022年4月发布的《城市轨道交通2021年度统计和分析报告》中数据，中国大陆地区已有50个城市开通城市轨道交通，运营线路283条， 运营线路总长9 206.8 km，当年新增运营线路1 237.1 km，新发展机遇也带来新挑战。高峰时段站内各通行设施处(楼扶梯、闸机、通道等)客流密度迅速增加，极易发生乘客拥堵、踩踏等事故[1]。对轨道车站客流疏散方案进行优化、科学疏散诱导，从而得到最小化疏散时间已成为疏散仿真研究中亟需解决的难题，引起了国内外学者的广泛关注。在模型与仿真技术方面：Gipps[2]最早建立一种简单的行人最短路径选择模型；随后，Nagel等[3]提出元胞自动机模型(CA)；Helbing等[4]研究行人交通流特性，提出社会力模型(SFM)。随着计算机技术发展，基于以上模型开发的仿真软件被学者广泛用于建筑物内人员疏散问题研究：陈利红[5]通过基于社会力模型驱动的Anylogic构建地铁站大客流换乘仿真模型，分析寻找疏散瓶颈，提出客流疏散优化方案；Bohari[6]基于SimWalk仿真，提出紧急情况下车站建筑内行人最短疏散路径；随后Bohari等[7]在此基础上，应用仿真软件对实际站内乘客行为数据进行疏散效果评估；Feng等[8]利用Anylogic完成建筑和行人行为建模，模拟行人疏散过程并提出优化方案；Avdeeva等[9]同样基于AnyLogic模拟建筑内人员疏散过程，得到出入口人流强度对疏散时间存在的影响；康元磊等[10]应用MassMotion进行客流疏散仿真建模，分析车站内设施、拥挤度和出口选择方式对疏散效率的影响。随着轨道交通迅速发展，紧急事件中站内客流疏散方案也成为研究热点：Frank等[11]研究室内构筑物与其附属设施对疏散效率的影响；Lei 等[12]通过对枢纽站进行客流疏散仿真，发现客流疏散时间与客流密度间的关系；侯正波等[13]分析紧急情况时上下行扶梯运行情况的合理性；刘杰[14]分析车站内不同层间和同层间不同基础设施的水平疏散效率；穆娜娜等[15]研究站台层扶楼梯处导流杆长度对乘客通过性的影响；李慧[16]通过增设指示标志增强基础设施的疏散通过能力；熊国强等[17]对西安地铁青龙寺站进行疏散仿真，认为乘客快速掌握出口信息是解决疏散瓶颈的关键；胥旋[18]研究站台层车门开启方式对乘客疏散的影响；郁奇涛等[19]指出地铁站内附属设施也是客流疏散效率的潜在影响因素；Huang等[20]提出疏散中语音警报设备布置和设计的有效方案。

综上，现有研究大多利用仿真软件内部建模功能搭建仿真场景，很少基于三维设计软件进行独立建模，且主要分析站内基础设施和附属设施布局与物理尺寸对客流疏散效果的影响。针对现有研究的不足，文中同时考虑三维建模精细程度和客流流线干扰策略对疏散效率的影响，通过观察疏散过程中客流流线情况寻找疏散瓶颈，提出优化方案并验证其有效性和可行性，为紧急情况下轨道车站客流的组织方式提供依据。

1 疏散效率影响因素分析

1.1 环境因素

车站建筑结构、基础设施布置方式等会对乘客疏散效率产生直接影响，该类因素即为环境因素,如出入口、检票闸机、楼扶梯、疏散通道等均会影响站内疏散效率[21]。相关实验表明，直线型出入口疏散效率高于“L”型和“T”型出入口，当疏散通道宽度足够大时，应尽量采用直线型出入口[22]。门扉式检票闸机的通过能力较好，在紧急情况下为避免检票闸机处排队拥堵，所有闸机应为持续开放状态，以提高疏散效率。自动扶梯可为乘客提供大面积的疏散渠道，但随着乘客群体恐慌程度的上升，使用自动扶梯的危险性也在上升，因此，自动扶梯上更容易发生踩踏事故。疏散通道尺寸设计的合理性和协调性要达到减少疏散时间目的，通道宽度设计应满足紧急事件下客流应急疏散要求，环境单一且步行条件较好是其设计的基本要求。

1.2 心理因素

除环境因素外，乘客心理也会对疏散路径选择和疏散效率产生影响。正常情况下，密集的乘客群体具有共同的方向性并遵循一定规律。如在通勤高峰时段内，站内乘客均以寻找合适的乘车点和出入口为目的，并在一定约束下形成良性流动方式，但在紧急情况下，一旦群体中的个体变得恐慌焦虑，整个群体将会处于混乱状态。现有研究中，恐慌、焦虑、冲动、从众等心理多被用作分析疏散效率影响因素的切入点[23]。但实际上直接影响疏散成功率的心理因素还有以下方面：

1)高密度的乘客群体易受环境刺激，难以主动克服疏散瓶颈障碍，而低密度的分散乘客能够抑制情绪冲动，从而提高疏散成功率；

2)密集的乘客群体易受个体情绪影响，紧急情况下偶尔会有乘客顾忌个人利益选择违背秩序。因此，车站客流密度越大，心理因素带来的负面影响越会具有危害性。

2 客流组织分析

轨道车站内乘客带有目的性的移动会产生一定的流动过程和流动路线，这种轨迹称为客流流线。流线设计是否合理，不仅影响客流集散效率，也直接关系到车站的服务质量和水平。

图1给出了理想状态下的客流流线，但实际上乘客都具有各自的行动轨迹，从而形成复杂的流线，而客流流线往往会出现冲突情况，从而降低车站内疏散效率。客流流线冲突分为流线汇合、流线交叉和多流线交织3种情况，如图2所示。流线冲突程度越复杂，说明客流混乱程度越大。

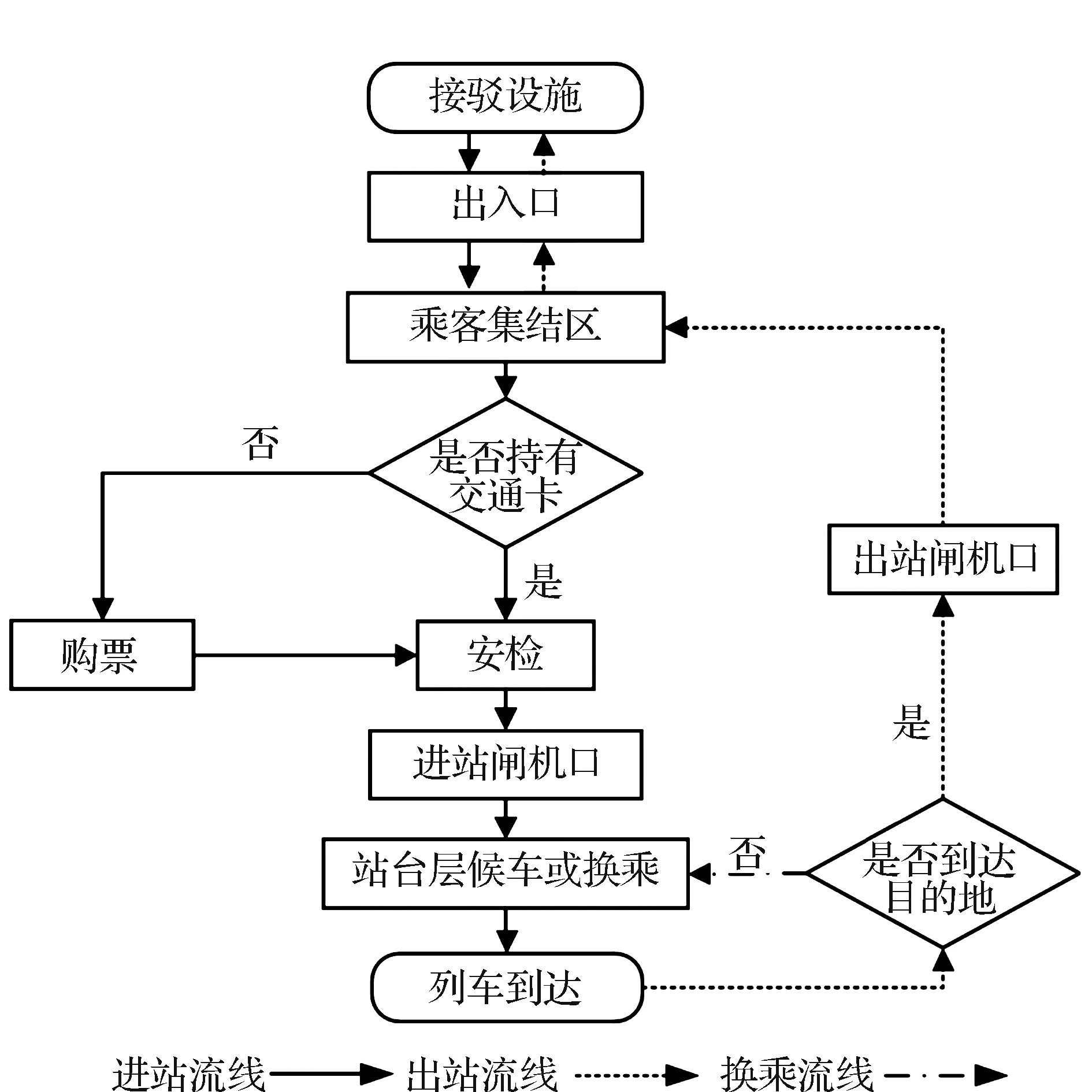
图1 轨道车站客流流线

图2 流线冲突

为避免平峰时段站内服务设施闲置，有效缓解高峰时段和突发情况下的客流疏散压力，目前轨道车站一般采用平峰时段关闭多余检票闸机口和疏散通道，高峰时段和突发情况下开放所有检票闸机口，并根据需要开放疏散通道。

3 应急疏散仿真

随着行人仿真领域的快速发展，Anylogic、Pathfinder等多款仿真软件在行人疏散仿真中得到广泛运用。Anylogic基于社会力模型的离散与混合系统进行建模和仿真，搭建过程复杂[24]。Pathfinder可根据现实建筑创建模型，并为模拟人员设置独立参数，模拟结果能够三维可视化，但软件内部建模精度较低[25]。而以社会力模型驱动、以路线成本法进行最短路径选择的MassMotion能根据仿真环境动态计算路线成本，从而实现最优路径实时更新，并兼容SketchUp三维建模软件导出的文件格式，因此，该软件在行人规划和疏散建模上具有优势[26]。文中借助SketchUp搭建高精度仿真模型，其后导入MassMotion进行仿真模拟，针对客流流线冲突情况提出优化方案并验证其可行性。

3.1 仿真模型建立

参照青岛地铁13号线董家口火车站地铁站，通过SketchUp搭建仿真实验场景。该地铁站为侧式高架站，地上一层为站厅层，图3给出了站厅层布局情况。站厅主体长75 m，宽24 m；自动检票口14个，出入站两侧各设置7个(每侧均有2个暂停使用)，宽0.55 m；无障碍通道2个(两侧各设置1个)，宽1 m；乘车通道2个，共两座上下行自动扶梯，宽2.8 m，单个梯级宽1 m；站厅两侧各有一个双向通行楼梯，宽2.4 m；应急通道1个，设置在站厅一侧。

地上二层为站台层：侧式站台主体长75 m，单侧宽6.4 m；站台最窄处宽3.4 m；主体两侧均有一处上下行自动扶梯，宽2.8 m，单个梯级宽1 m。站台层至站厅层主要通过每侧的自动扶梯与楼梯进行转换，升降电梯作为辅助转换设施。站台层布局情况如图4所示。

图3 站厅层平面

图4 站台层平面

将如图5所示的车站模型导入MassMotion中，并将模型中各个独立物件分别转换为楼面、出入口、连接处、通道、障碍物等，完成仿真软件可用的高精度模型创建。由于侧式站台能有效缓解客流流线冲突，站台层疏散能力本身具有一定的优势，因此重点分析对象为设施布局较为复杂的站厅层。

图5 车站模型

3.2 突发情况下仿真参数设定

3.2.1 人物属性参数设定

根据文献[21]所述，站内高峰时段和紧急情况下乘客走行速度维持在0.80～1.78 m·s-1之间，总体步速在均值1.25 m·s-1上下浮动，且遵循标准差为0.17的正态分布，据此对人物进行速度设置。

3.2.2 疏散参数设定

仿真车型设定为B型4编组车，列车满载量为950人。考虑到该车站运营现状，设定到站乘客数和候车乘客数均为475人，车门开关间隔为20 s。在到站的一侧站台，将在20 s内生成475个个体；在候车的一侧站台，共有475个个体正在等待。在疏散开始时，乘客有一定的等待时间，移动前等待时间符合均值为45 s、标准差为0.15的正态分布，等待方式为分散。仿真模拟中均选择以到达目的地时成本最低为疏散分配方式。

3.2.3 出入口设定

该仿真模型中的入口设置为产生乘客的输出点，出口设置为乘客消失点。由于该列车为B型4编组车，所以站台层列车到站一侧设16个乘客输出点，共产生475个个体。考虑到乘客就近候车心理，在候车一侧站台的自动扶梯和楼梯口附近分别设置一个乘客产生点，乘客围绕该点堆积并向周围站台扩散。出口有2个，分别为站厅层出入口和应急通道。

3.3 仿真模拟

3.3.1 原有方案仿真模拟

紧急情况下进站闸机均作为出站闸机使用，可供疏散的闸机口共14处，2处无障碍通道开启，单侧应急通道开启，安检区域部分隔离栏撤离，如图6所示。仿真过程中，到站乘客与候车乘客均需通过自动扶梯和楼梯疏散至站厅层，用时3.35 min；而乘客从站厅层全部疏散至户外时才算完成疏散任务，至疏散任务完成共用时7.62 min。

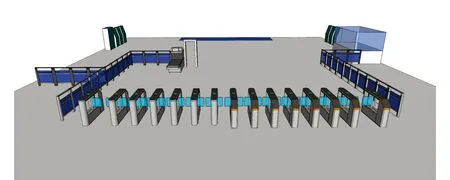
图6 原有方案设施布局

3.3.2 优化方案仿真模拟

根据原有疏散方案的仿真结果，制作客流流线图，观察图7(a)可发现疏散瓶颈所在位置和利用率较低的疏散设施。当站台两侧乘客下至站厅层时，候车乘客更倾向于以下3种选择：正对出入口的中间闸机；率先出现在视线内的单侧应急通道(图7(a)中矩形标注处)；靠近安检区域和楼梯口的闸机和无障碍通道(图7(a)中圆形标注处)进行疏散。而到站乘客会就近选择应急通道，也会选择中间部分或靠楼梯最近的闸机及无障碍通道进行疏散。

图7 不同疏散方案客流流线对比

1)优化方案一。 通过观察客流流线，发现在原有方案下中间部分的闸机通道和单侧应急通道均发生了严重的流线冲突，而部分闸机通道未得到利用。因此，可针对客流流线冲突情况对原有疏散方案进行优化。

优化策略：在站厅层乘客集聚区域增设隔离栏，对客流流线产生干扰，从而使冲突的流线进行重组。由于应急通道处最具有吸引力，流线冲突最为严重，因此考虑在此增设隔离栏作为干扰物，如图8所示。隔离栏的增设一方面用于干扰原有客流流线，另一方面用于疏导乘客，使其有序疏散至户外。在该优化策略下，不同于原有方案仿真结果的是至疏散任务全部完成共用时5.63 min。此时观察如图7(b)所示的客流流线，发现候车乘客对通道的选择分布大致处于均衡水平。比起原有方案，到站乘客会更多地选择中间部分闸机通道和靠近安检区域的闸机通道，缓解了单侧应急通道疏散负担，减轻了客流流线冲突的严重程度。

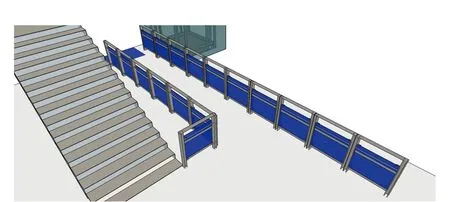
图8 应急通道增设护栏

2)优化方案二。 该优化方案是在方案一的基础上进行，优化策略：另外增设隔离栏，可使到站乘客和候车乘客分开疏散，如图9所示。在该优化策略下疏散任务完成时间较方案一发生了变化，共用时5.70 min。

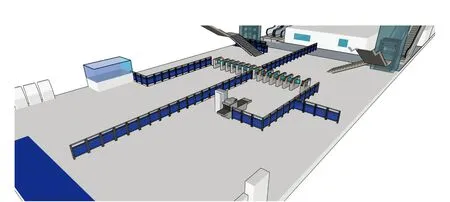
图9 站厅增设隔离栏

此时再观察图7(c)所示的客流流线，发现候车乘客与到站乘客的客流流线互不干扰，有效防止了流线冲突造成的疏散瓶颈，但仍有部分通道未得到利用，且疏散时间比方案一略长。

3)优化方案三。 该方案优化策略：设置隔离栏阻断楼扶梯乘客冲突，走自动扶梯的乘客仅以应急通道为出口，走楼梯的乘客通过闸机，仅通过出入口疏散至户外，如图10所示。在该策略下完成疏散任务用时最少，共用时5.43 min。

图10 隔离栏阻断楼扶梯乘客冲突

在如图7(d)所示的客流流线中，站厅层未出现流线冲突情况，但站台层仍会出现一定程度的流线冲突，这是由于站台楼梯或自动扶梯口拥堵，站台中部的乘客根据环境对最优疏散路径进行实时决策。

3.4 仿真结果对比分析

3.4.1 寻路方法及理论计算

1)路径成本法。 MassMotion基于路线成本法选择行人最短走行路径。仿真过程中行人考虑起点到出口的距离、地形、站内设施布局等因素，动态计算路径成本，对最优路径进行实时决策。路径成本函数如式(1)所示。

(1)

式中：C为总行程时间；WD为DF的距离权重；DF为行人产生位置到目标位置的距离；V为行人预期走行速度均值；WQ为列队权重；TQ为到达目标位置之前队列中预期消耗时间；WG为几何组件遍历权重；CG为几何组件类型成本。

结合路径成本法中考虑的因素，仿真模型中行人路径选择流程如图11所示，该图描述了行人由出发点到两个出口的路径选择过程，出口分别由n和n+1表示。

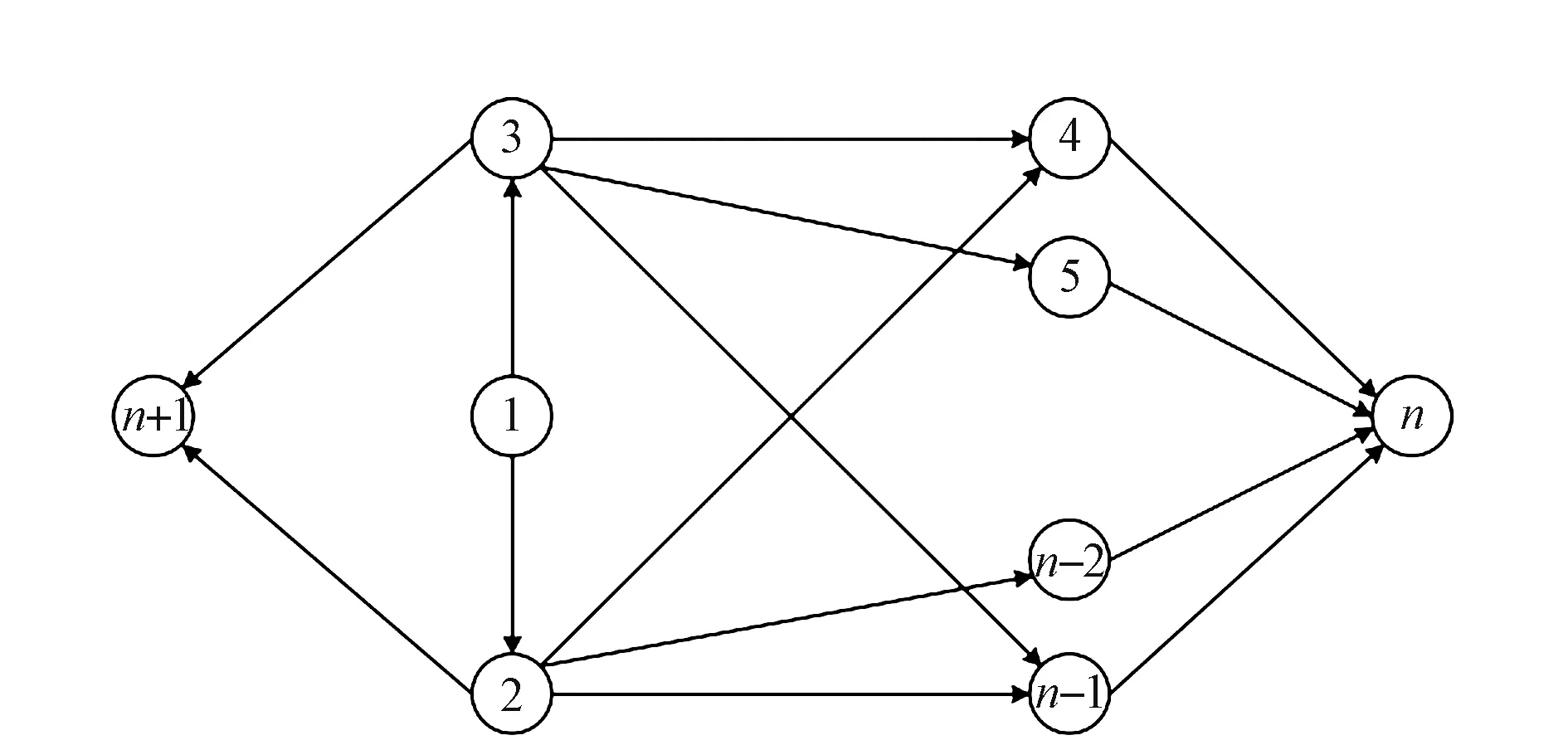
图11 行人路径选择流程

2)安全疏散理论公式。 根据《地铁安全疏散规范》(GB/T 33668-2017) 第5.7和5.8条规定：站台层事故疏散时间应满足在6 min内将乘客全部撤离至站厅层的要求；站厅层事故疏散也应保证在6 min之内全部完成。站台层和站厅层安全疏散时间分别按式(2)～(3)计算。

TS=TS1+TS2+TS3+TS4+TS5<6 min

(2)

TC=TS+TC1+TC2+TC3<6 min

(3)

式中：TS1为探测报警时间及人员预动作时间之和；TS2为乘客疏散至楼扶梯入口时间；TS3为乘客通过楼扶梯时间；TS4为楼扶梯上乘客平均滞留时间；TS5为通道非均匀性偏差时间；TC1为站厅层乘客行走时间；TC2为乘客通过闸机时间；TC3为乘客通过安全出口(出入口与应急通道口)时间。

根据《地铁安全疏散规范》中提供的公式，计算得到如表1～2所示的各变量结果。站台层安全疏散时间TS和站厅层安全疏散时间TC分别为3.21 min和5.82 min。

表1 站台层安全疏散时间理论计算 min

表2 站厅层安全疏散时间理论计算 min

3.4.2 对比分析

对比原有方案和优化方案下的应急疏散仿真结果。图12给出了不同疏散方案下未疏散乘客数随疏散时间的变化情况。原有方案下乘客从站台层疏散至站厅层用时3.35 min，至疏散任务全部完成共用时7.62 min。在以设定相同计划疏散乘客数量为前提的3种优化方案下，疏散任务全部完成用时分别为5.63 min、5.70 min和5.43 min，优化率分别为26.12%、25.20%和28.74%。且由已知条件，根据理论公式计算得到疏散时间为5.82 min。

仿真结果与计算结果表明，《地铁安全疏散规范》理论计算时间和3种优化方案模拟时间均小于6 min，且结果较为一致，满足国家标准规定。由于《地铁安全疏散规范》考虑了乘客心理、车站环境、通道非均匀性偏差时间等多种疏散影响因素，计算得到所需疏散时间较长。通过对比发现，虽然方案二防止了客流流线冲突，但在优化率和经济成本方面不如方案一和方案三。在方案一中，在开放所有通道的基础上，在单侧应急通道处增设护栏进行客流疏导，虽然该措施对车站内环境影响较小且减轻了客流流线冲突程度，但除应急通道处其他区域客流混行程度有所上升。在方案三中，楼扶梯乘客分类疏散，有效防止了客流流线冲突，不仅避免了乘客混行情况下存在的安全隐患，其优化率也达到最高的28.74%。综上所述，选取优化方案三作为最优方案。对比结果如表3所示。

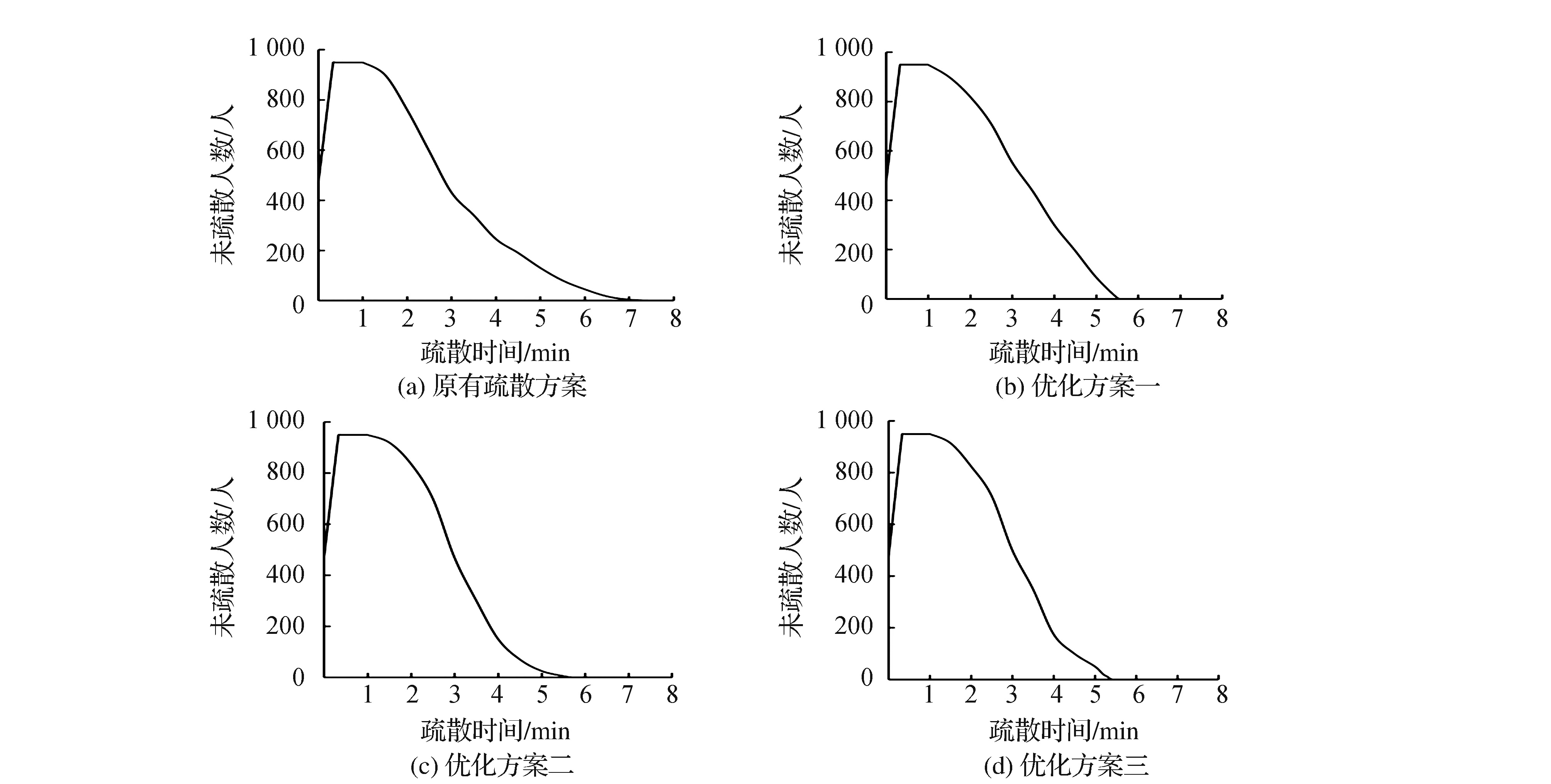
图12 不同疏散方案下车站内乘客疏散情况

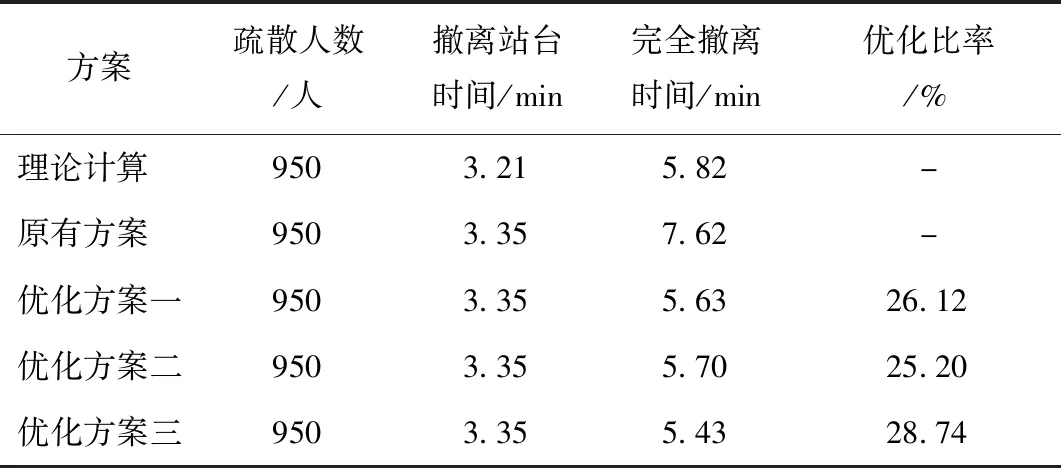
表3 疏散结果统计

4 结 论

文中考虑以流线干扰策略对原有疏散方案进行优化，最后通过对比分析优化前后的疏散结果及理论计算值，验证优化方案的可行性和有效性。有待进一步解决的问题有以下几点：

1)疏散过程中检票闸机未得到充分利用，未来研究可针对闲置通道对疏散方案进行优化；

2)仿真中行人路径选择主要是基于对道路连通性和畅通性的判断，为进一步还原乘客的实时决策行为，可通过编写计算机程序对仿真平台进行二次开发；

3)基于启发式算法求解优化路径，能更好地体现优化方案的有效性和可行性，具有进一步的研究价值。