基于多项式求根的双厚度透射率模型确定光学常数

杨百愚，武晓亮，王翠香，王伟宇，李 磊，范 琦，刘 静

〈系统与设计〉

基于多项式求根的双厚度透射率模型确定光学常数

杨百愚，武晓亮，王翠香，王伟宇，李 磊，范 琦，刘 静

（空军工程大学 基础部，陕西 西安 710051）

为解决光谱反演法确定物质光学常数的一些问题，基于传统的双厚度透射率模型，建立厚度分别为和2的光谱透射率方程，通过代数运算获得与衰减系数有关的八次多项式方程，求解并选择其大于0小于1的实数根来计算衰减系数和消光系数；再求解关于界面反射率的一元二次方程，选择其大于0小于1的根来计算折射率。在确定光学常数的过程中，新方法没有反演误差和迭代计算耗时问题。利用已知文献中庚烷的光学常数验证新方法的可靠性，并分析了双厚度不满足2倍关系时对计算结果的影响，结论是第二厚度2的相对误差不超过1%时，消光系数的计算误差不超过2.03%，不考虑3个强吸收点时，折射率的计算误差不超过1%。

光学常数；折射率；消光系数；衰减系数；双厚度透射率模型

0 引言

折射率和消光系数称为物质的光学常数，这两个参量是随光波长变化的，但习惯称为常数。在电磁波理论中，光谱反射率和透射率等光学性质可用物质的光学常数来描述，因此可通过测量光学性质来确定光学常数。方法主要有双光谱反演法[1]、反射光谱反演法[2]、透射光谱反演法[3-5]、双厚度透射光谱反演法[6-7]。

Bohren和Huffman[8]用电磁波理论建立了平板材料的光谱透射率模型、以及只考虑光在平板内的多次反射，而忽略干涉效应时的非相干透射率模型。基于前者，Tuntomo[6]等人采用玻璃-液体-玻璃三层平板结构，测量两个不同厚度液体的光谱透射率，在忽略玻璃影响的情形下通过迭代法反演确定了碳氢燃料庚烷和癸烷的光学常数。基于非相干透射率模型，李全葆等人[7]通过测量不同厚度碲镉汞晶片的光谱透射率，采用迭代法求解了碲镉汞的光学常数；苏星等人[9]测量了一种红外硒化物玻璃的光学常数。李栋等人[10-12]以上述研究为基础，提出了多种改进透射率模型及反演算法，提高了三层平板结构测量液体光学常数的精度；王程超等人[13]基于射线踪迹法推导了三层结构系统的总透射率模型，并采用粒子群优化算法（Particle Swarm Optimization, PSO）进行反演计算了生物柴油的光学常数。

因为多层结构的存在，上述测量液体光学常数的透射率模型和反演算法较为复杂。但对于半透明固体材料，如石英、金刚石、砷化镓、氟化镁和硒化锌等红外光学材料在光学窗口、像质改善和液体光学测量等方面有重要应用。这类固体材料可制备成单一材料结构并基于双厚度透射率模型测量其光学常数，这种情况下主要研究反演算法。如李栋等人[14-15]提出了简化方程迭代法（Simplifie-Equation Iterative, SEI）和蒙特卡洛法（Monte-Carlo, MC）；吴国忠等人[16]对SEI、MC和PSO三种方法做了比较研究，结论是PSO方法精度更高。

使用反演迭代法确定光学常数的方法计算耗时且存在迭代误差，上述学者在反演算法的设计、精度提升及误差减小上做了很多研究，但直接去求解双厚度透射率方程的尝试还未见报道。本文在这一方面做了探索，只要将双厚度透射率模型中的两个厚度设定为2倍关系，则经过代数推导，即可获得与衰减系数（可换算出消光系数）有关的八次多项式方程，以及关于界面反射率的一元二次方程。这两个方程均可求得精确数值解或解析解，从而避免了反演算法的耗时和误差。本文以文献[6]中庚烷的光学常数作为“理论值”，代入双厚度透射率方程计算的透射率作为“实验数据”，用多项式求根的方法确定庚烷的折射率和消光系数，验证了本文方法的可靠性。最后分析了双厚度偏离2倍关系时对计算结果的影响。

1 多项式求根的双厚度透射率模型

设半透明平板材料的折射率、消光系数分别为和，则衰减系数＝4p/，其中为光波长。将平板材料置于空气（折射率为1，消光系数为0）中，当光线垂直入射时，根据菲涅耳定律和斯涅耳定律，在平板材料与空气分界面上的界面反射率＝[(－1)2＋2]/[(＋1)2＋2]。由于平板材料有两个界面，考虑光在平板内的多次反射，而忽略干涉效应时，光垂直通过厚度为L的平板后的透射率T可表示为[8]：

则光通过厚度为和2的平板材料后的透射率和分别用式(2)、式(3)表示：

＝(1－)2/(1－22) (2)

＝(1－)22/(1－24) (3)

式中：＝exp(－)。给式(2)两侧同乘以，联立式(3)消去两式右侧的分子，有：

－＝(－2)22(4)

将式(4)中的代入式(2)，经过代数运算可得：

()＝88＋77＋66＋55＋44＋33＋22＋

1＋0＝0 (5)

式中：8＝2，7＝－2(1＋)，6＝2(1＋)2，5＝2(1＋)，4＝－2(2＋22＋2)，3＝2(1－)，2＝2(1－)2，1＝－2(1－)，0＝2，式(5)是关于的一元八次多项式方程，通过数值求解可得到其8个根，但只有满足0＜＜1的根才有实际物理意义。则平板材料的衰减系数和消光系数分为：

＝－ln()/(6)

＝－ln()/(4p) (7)

另由式(2)可得：

2(2＋)－2＋(－)＝0 (8)

式(8)是关于的一元二次方程，由于其判别式非负，又因0＜＜1，则方程(8)的解为：

则平板材料的折射率为：

只要测量出、2两种厚度下的光谱透射率、，可由式(5)求多项式方程的根，再由式(6)、式(7)和式(10)计算出衰减系数、消光系数和折射率。上述方法不必经过耗时的反演迭代来确定光学常数（多项式求根所用计算时间可忽略不计），所以结果中不存在反演误差。

2 结果和讨论

本文采用文献[6]中庚烷在2.5～15mm的光学常数作为“理论值”。将上述光学常数代入式(2)、式(3)，计算厚度分别为＝15mm和2＝30mm下的透射率作为“实验数据”，然后利用多项式求根的方法确定庚烷的光学常数，通过比较计算结果与理论值的相对误差来验证本文方法的可靠性。需要指出，由于本文透射率模型与文献[6]的透射率模型不同，这里的“实验数据”与文献[6]的真实实验数据是有差别的。此处仅是借用文献[6]的数据构造了适合本文透射率模型的“实验数据”来代替实际实验，其好处是可以避免实际实验的其他误差而专门研究多项式求根方法的可靠性。

基于多项式求根方法确定的庚烷光学常数如图1所示，消光系数有3个峰值，对应3个强吸收带。从消光系数和折射率的相对误差可以看出计算结果与理论值符合得很好，其中消光系数的最大相对误差为－9.4×10－7%，折射率的最大相对误差为1.4×10－5%。结果表明本文方法确定光学常数没有反演迭代误差。

图1 基于多项式求根方法确定文献[6]中庚烷的光学常数

由于本文方法要求材料的两个厚度成2倍关系，如果第二厚度的制备或测量存在误差，则会导致计算结果出现误差。假定第二个厚度2存在1%和5%的误差，则实际的厚度为(2±0.02)和(2±0.1)，不妨取1.98和1.9，则相应的透射率为¢＝(1－)21.98/(1－23.96)和²＝(1－)21.9/(1－23.9)。将文献[6]中庚烷的光学常数代入此处公式计算的透射率作为“实验数据”，但仍按照基于2倍厚度关系推导的多项式方程来计算光学常数，通过比较计算结果与理论值的相对误差来评估厚度偏离2倍关系时对计算结果的影响，结果分别如图2、3和图4、5所示。

如图2、3所示，第二个厚度2存在1%的误差时，消光系数的相对误差在(2～2.03)%之内，而折射率在3.4mm、6.8mm、13.8mm吸收带的误差较大，分别为26.9%、3.8%和1.3%，其余波长处的误差不超过1%。可见，不考虑强吸收点，就整个波段范围来看，由于厚度不满足2倍关系对消光系数计算结果的影响大于折射率；但在强吸收点，同样的厚度改变，由于值较大所造成的透过率的相对误差就比较大，折射率的计算对此比较敏感，而消光系数的计算却不敏感。

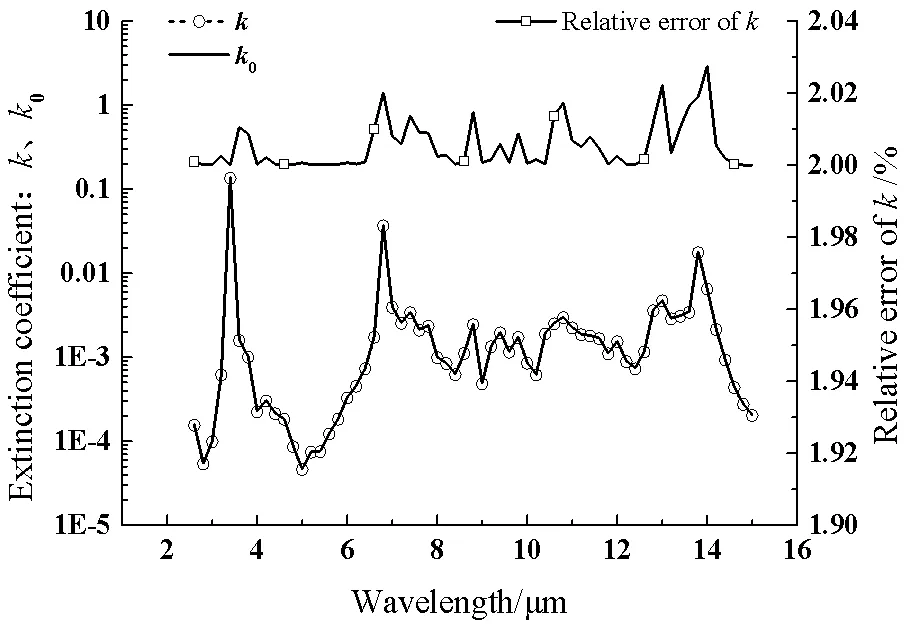
图2 第二厚度2L存在1%误差时k的计算误差

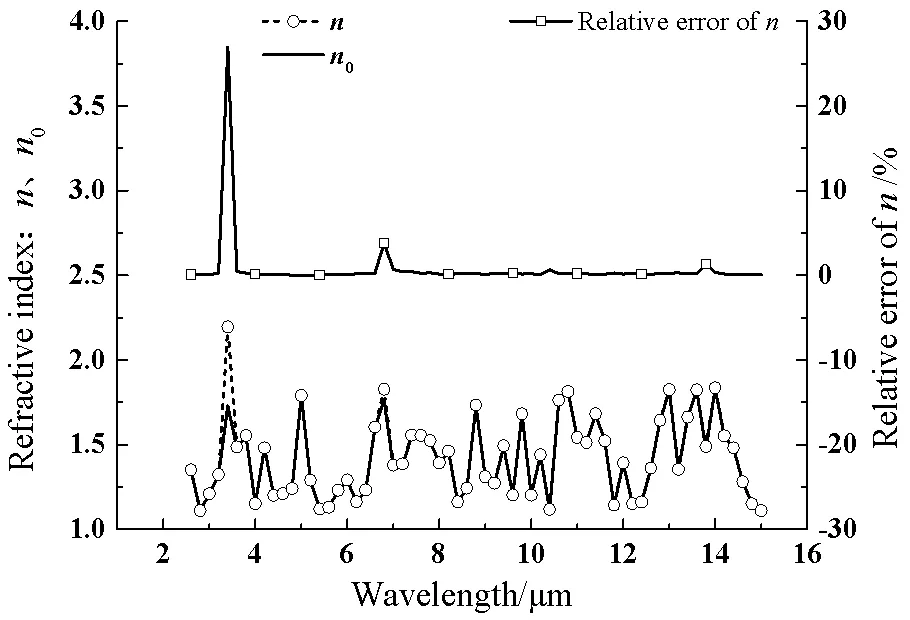
图3 第二厚度2L存在1%误差时n的计算误差

如图4、5所示，第二个厚度2存在5%的误差时，消光系数的相对误差在(10～10.15)%之内，而折射率在3.4mm、6.8mm、13.8mm吸收带的误差较大，分别为134.9%、18.5%和6.4%，其余波长处的误差不超过3.5%。其结论与厚度存在1%误差时的情形相似。再比较厚度误差1%和5%的计算结果，可以看出当厚度误差扩大5倍时，消光系数、强吸收点折射率的计算误差也扩大5倍左右，但其余波长处折射率的计算误差仅扩大3.5倍，对厚度的误差相对不敏感。

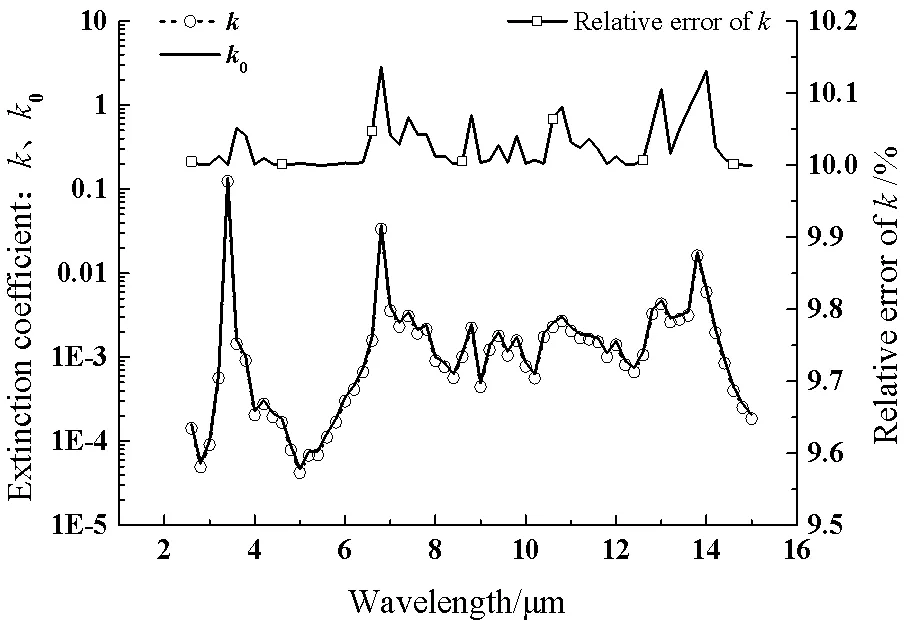
图4 第二厚度2L存在5%误差时k的计算误差

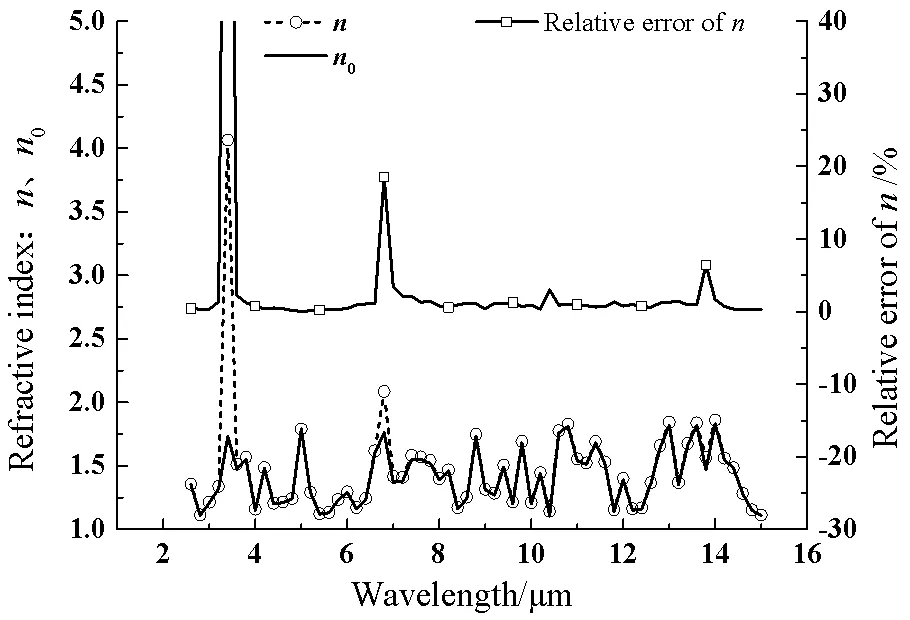
图5 第二厚度2L存在5%误差时n的计算误差

3 结论

基于传统的双厚度透射率模型，在将两个厚度设定为2倍关系时，可获得与衰减系数有关的八次多项式方程，以及关于界面反射率的一元二次方程。通过多项式方程求根的方法实现了光学常数的确定，从而避免了反演迭代法的耗时和误差。借用文献[6]中庚烷的光学常数验证了本文方法的可靠性，除了个别的强吸收点，即使模型中的两个厚度偏离2倍关系时本方法仍能获得较好的计算结果。

[1] El-Zaiat S Y, El-Den M B, El-Kameesy S U, et al. Spectral dispersion of linear optical properties for Sm2O3doped B2O3-PbO-Al2O3glasses[J]., 2012, 44: 1270-1276.

[2] Bridou F, Cuniot-Ponsard M, Jean-Michel D. Experimental determination of optical constants in the vacuum ultra violet wavelength region between 80 and 140 nm: a reflectance versus thickness method and its application to ZnSe [J]., 2007, 271: 353-360.

[3] Dhanasekaran V, Mahalingam T, Rhee J K, et al. Structural and optical properties of electrosynthesized ZnSe thin films[J]., 2013, 124(3): 255-260.

[4] 王贵全, 张锦荣, 邵毅, 等. 基于透射光谱的类金刚石膜光学参数反演[J]. 红外技术, 2021, 43(5): 473-477.

WANG G, ZHANG J, SHAO Y, et al. Calculation of Optical Parameters of Diamond-like Carbon Film Based on Transmission Spectrum [J]., 2021, 43 (5): 473-477.

[5] 侯典心, 路远, 宋福印. 基于全光谱拟合法的VO2薄膜光学常数计算[J]. 红外技术, 2017, 39(3): 243-249.

HOU D, LU Y, SONG F. Optical constants of VO2thin films based on whole optical spectrum fitting., 2017, 39 (3): 243-249.

[6] Tuntomo A, Tien C L, Park S H. Optical constants of liquid hydrocarbon fuels[J]., 1992, 84: 1-6, 133-140.

[7] 李全葆, 宋炳文, 魏天衢. Hg(1-x)CdTe光学常数测量[J]. 红外技术, 1991, 13 (5): 17-20.

LI Q, SONG B, WEI T. The measurement of optical constants of Hg(1-x)CdxTe [J]., 1991, 13 (5): 17-20.

[8] Bohren C F, Huffman D R.[M]. New York: John Wiley & Sons, 1983: 36-41.

[9] 苏星, 李正芬, 刘成赞, 等. 一种红外硒化物玻璃的光学常数及其增透膜[J]. 红外技术, 1996, 18(5): 15-18.

SU X, LI Z, LIU C, et al. Optical constants of a Selenide glass and its AR coatings., 1996, 18 (5): 15-18.

[10] 李栋, 齐晗兵, 吴国忠. 柴油的透射光谱测量和热辐射物性参数反演[J]. 光谱学与光谱分析, 2015, 35(3): 719-723.

LI D, QI H, WU G. Transmittance spectra measurement and thermal radiative physical parameters inversion of diesel fuel[J]., 2015, 35(3): 719-723.

[11] 李栋, 艾青, 夏新林. 液态碳氢燃料热辐射物性参数反演方法[J]. 航空动力学报, 2012, 27(8): 1712-1717.

LI D, AI Q, XIA X. Inverse method investigation of thermal radiation property of liquid hydrocarbon fuel[J]., 2012, 27(8): 1712-1717.

[12] 李栋, 艾青, 夏新林. 透射法测量半透明液体热辐射物性的双厚度模型[J]. 化工学报, 2012, 63(S1):23-129.

LI D, AI Q, XIA X. Double-thickness model of thermal radiation physical property measurement of semi-transparent liquid with transmission method[J]., 2012, 63 (S1): 123-129.

[13] 王程超, 李兴灿, 谭建宇, 等. 生物柴油光学常数的双光程法实验测量[J]. 激光与光电子学进展, 2015, 52(5): 051206.

WANG C, LI X, TAN J, et al. Experimental measurement of optical constant of biodiesel by double optical pathlength transmission method[J]., 2015, 52(5): 051206.

[14] 李栋, 艾青, 夏新林. 利用透射光谱反演硒化锌的光学常数[J]. 光谱学与光谱分析, 2013, 33(4): 930-934.

LI D, AI Q, XIA X. optical constants determination of Zinc Selenide by Inversing transmittance spectrogram., 2013, 33 (4): 930-934.

[15] 李栋, 夏新林, 艾青. 两种反演半透明液体光学常数的方法对比[J]. 哈尔滨工业大学学报, 2012, 44(9): 73-77.

LI D, XIA X, AI Q. Comparison of two inversion methods on optical constants of semitransparent liquid., 2012, 44 (9): 73-77.

[16] 吴国忠, 胡鑫浩, 齐晗兵, 等. 基于粒子群算法反演液体光学常数新方法[J]. 光学与光电技术, 2018, 16(4): 23-29.

WU G, HU X, QI H, et al. A new method based on particle swarm optimization to invert liquid optical constants [J]., 2018, 16 (4): 23-29.

Determination of Optical Constants by Double Thickness Transmittance Model Based on Polynomial Root

YANG Baiyu，WU Xiaoliang，WANG Cuixiang，WANG Weiyu，LI Lei，FAN Qi，LIU Jing

(Fundamentals Department, Air Force Engineering University, Xi'an 710051, China)

To solve some problems in the determination of substance optical constants by spectral inversion, based on the traditional double thickness transmittance model, spectral transmittance equations with thicknesses ofand 2are established. The eighth-order polynomial equation related to the attenuation coefficient is obtained through an algebraic operation. Real roots greater than 0 and less than 1 are solved to calculate the attenuation coefficient and extinction coefficient. Then, the quadratic equation with one unknown quantity about the interface reflectivity is solved, and the roots greater than 0 and less than 1 are selected to calculate the refractive index. In the process of determining the optical constants, the new method has no inversion error or iterative calculation time-consuming problems. The reliability of the new method is verified using the known optical constants of heptane from the literature, and the influence on the calculation results was analyzed when the double thickness does not satisfy the double relationship. In conclusion, when the relative error of the second thickness 2was no more than 1%, the calculation error of the extinction coefficient was no more than 2.03%, and when three strong absorption points were not considered, the calculation error of the refractive index was no more than 1%.

optical constants, refractive index, extinction coefficient, attenuation coefficient, double thickness transmittance model

O433.1；O434.3

A

1001-8891(2023)01-0091-04

2022-01-06；

2022-04-11.

杨百愚（1973-），男，副教授，研究方向为红外材料特性、光电检测与信息处理技术。E-mail：yby0002@163.com.

范琦（1972-），男，副教授，研究方向为光电检测与信息处理技术。E-mail：af-fanqi@126.com.

国家自然科学基金（12004437）。