一种优化的GA-KF与BP-Adaboost地表下沉组合预测模型

张 灿 吕伟才 郭忠臣,4 刘 宇 谢世成

1 安徽理工大学空间信息与测绘工程学院，安徽省淮南市泰丰大街168号，232001 2 安徽理工大学矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室，安徽省淮南市泰丰大街168号，232001 3 安徽理工大学矿区环境与灾害协同监测煤炭行业工程研究中心，安徽省淮南市泰丰大街168号， 232001 4 宿州学院环境与测绘工程学院，安徽省宿州市汴河中路49号，234000

自动化GNSS监测系统可为矿区开采引起的地表变形提供连续监测数据，对监测数据进行分析处理，建立地表下沉预测模型，能够有效保障矿井安全生产，减少地表开采沉陷对人们生产生活的影响[1]。

地表沉陷变形预测的方法主要有神经网络模型[2]、灰色系统模型[3]、卡尔曼滤波[4]等，但这些模型均存在一定局限性。周纯择等[2]利用BP神经网络对盾构施工引起的地表沉降进行预测，预测效果较好，但BP神经网络本身收敛速度慢，容易陷入局部极小值；刘茂华等[3]利用灰色模型方法预测高层建筑物沉降，对其施工监测具有指导意义，但灰色系统模型仅适用于原始数据干扰较小且具有良好光滑性能情形；陈小杰等[4]利用卡尔曼滤波对上海某历史建筑在基础托换期间的沉降监测数据进行滤波和预测，取得较好效果，模型精度受系统噪声和观测噪声的影响较大，当噪声统计特性不明确即系统噪声和观测噪声无法精确获得时，预测精度会随之降低。对包含各种随机干扰因素(如采深、采厚、煤层倾角、开采速度等)的GNSS自动化监测系统进行地表下沉预测，采用单一预测方法时精度难以提高，因此寻求一种可以综合多个模型优点，有效提高预测效果的组合预测模型具有重要意义。

针对以上问题，本文提出一种地表下沉组合预测模型。首先根据小波变换理论[5]，运用Mallat算法对GNSS CORS自动化监测站数据进行分解，得到蕴含不同时频特征的随机序列和趋势序列，使不同序列内部拥有更多相似特征。由于卡尔曼滤波具有数据存储量小、精度高的优点，选用卡尔曼滤波对趋势项进行预测，同时采用遗传算法(GA)对系统噪声和观测噪声进行寻优，克服地表下沉过程中噪声统计特性不明确的影响，构造GA-KF模型。BP-Adaboost神经网络具有较强的非线性映射能力[6]，能够克服BP神经网络容易陷入局部极小值的问题，选用BP-Adaboost神经网络对随机项进行预测，同时运用混沌理论对随机项进行相空间重构，构造相空间重构BP-Adaboost模型。因此，本文分别使用GA-KF模型和相空间重构BP-Adaboost模型对趋势序列和随机序列进行预测，然后将趋势序列和随机序列预测值进行叠加，作为原始监测数据的一步预测值。

1 预测方法和原理

1.1 小波变换

根据GNSS监测数据特征，选取合适的小波基函数确定最佳分解层数，通过小波变换将原始监测数据f(t)分解成若干趋势序列s(t)和随机序列n(t)之和：

f(t)=s(t)+n(t)

(1)

重构得到的随机序列和趋势序列分别为d1,d2…dj和aj。

1.2 GA-KF模型

趋势项采用GA-KF模型进行预测。以某一监测站为例，卡尔曼滤波的动态离散系统函数模型可表示为:

(2)

式中，Xk为k时刻的系统状态向量，Φk,k-1为k-1到k时刻的系统转移矩阵，Γk,k-1为k-1时刻的系统噪声系数阵，Wk-1为系统噪声向量，Bk为k时刻观测矩阵，Vk为k时刻观测噪声向量，Lk为k时刻观测值。

与式(2)对应的卡尔曼滤波递推公式为：

(3)

(4)

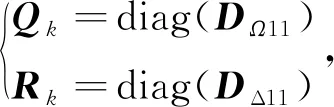
(5)

式中，n为数据样本。按所选择的适应度函数采用遗传算法中复制、交叉及变异对个体进行筛选，通过不断迭代，直至满足终止条件，求得最优Q、R值，建立GA-KF预测模型进行一步预测。

1.3 相空间重构BP-Adaboost模型

BP-Adaboost模型是把单独一个BP神经网络看成弱预测器，对BP神经网络反复训练以预测样本输出，再通过Adaboost算法将多个BP神经网络加权组合成一种强预测器，最后输出训练结果[8]。

假设随机序列为{x(i),i=1,2,…,N}，N为该序列长度。采用坐标延迟法完成相空间重构，得到重构后的m维相空间Yj={xj,xj+τ,…,xj+(m-1)τ},其中j=1,2,…,M，并构造如式(6)所示映射作为BP-Adaboost模型的输入与输出，构建相空间重构BP-Adaboost模型对随机序列进行预测。

(6)

式中，相点个数M=N-(m-1)τ，嵌入维数m和延迟时间τ分别采用G-P算法和自相关函数法获取[9-10]。

1.4 组合预测模型

将趋势项预测值与随机项预测值求和作为该组合模型的最终预测值。具体构建流程如图1所示。

图1 模型构建流程Fig.1 Flowchart of model construction

2 工程实例

选取监测站观测时间为2021-09-12～11-27，观测间隔为6 h，共305期(编号为1～305)高程分量监测值作为实验数据。首先以最近连续100期(编号为201～300)数据为例，对最后5期数据进行一步预测；再研究不同长度时间序列数据建模对预测精度的影响，划分5种预测任务：分别选取连续300期(编号1～300)、200期(编号101～300)、150期(编号151～300)、100期(编号201～300)、50期(编号251～300)监测数据对最后5期进行预测。

2.1 建模预测

首先利用db4正交小波对监测站201～305期数据进行2～5层分解与重构。根据去噪前后信噪比最高、均方误差最小的原则，确定分解层数为3层，并得到趋势项序列a3和随机项d1、d2、d3，趋势项和随机项提取结果见图2。对于趋势项a3，利用GA-KF模型进行一步预测，得到趋势项预测值，其中遗传算法的最大迭代数为100，种群规模为30，交叉和变异概率分别为0.5和0.01。对于各随机项d1、d2、d3，采用相空间重构BP-Adaboost预测模型进行一步预测。

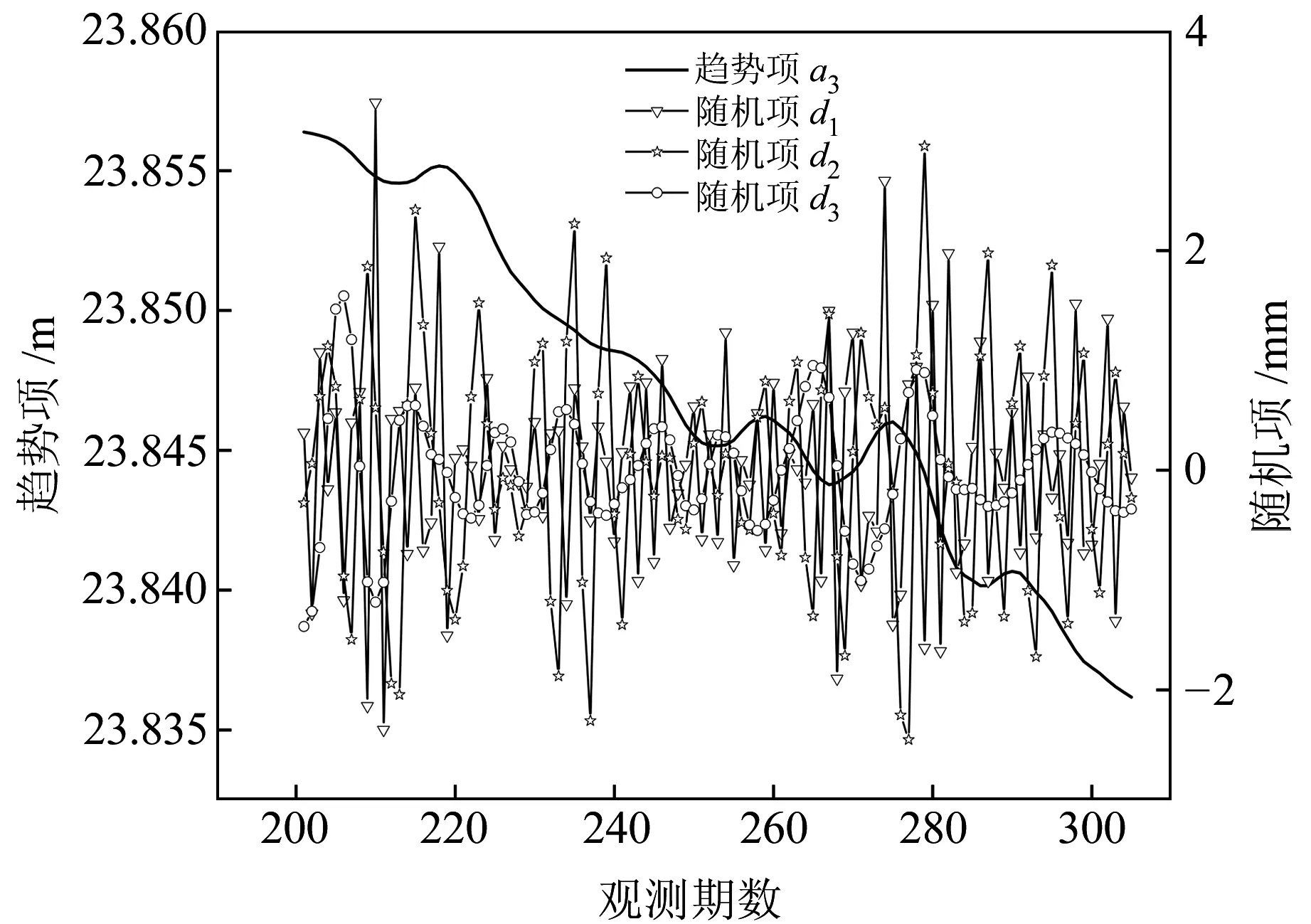
图2 趋势项与噪声项Fig.2 Trend and noise term

以随机项d1为例进行相空间重构。首先采用G-P算法和自相关函数法确定随机项d1的嵌入维数m和延迟时间τ。由G-P算法得到lnC(r)与lnr的关系如图3所示，从图中可以看出，随着嵌入维数m增大，当m取7～10时双对数曲线中直线段部分的斜率(即关联维的大小)基本保持不变(达到饱和)，取第1次达到饱和时的嵌入维数m=7，计算出关联维D=2.85，为非整数，说明该随机项具有混沌特性，可以进行相空间重构。将重构后的m维数据作为BP-Adaboost模型的输入值进行预测，得到随机项d1的预测值。

图3 lnC(r)与lnr关系曲线Fig.3 Relationship between lnC(r) and lnr

BP-Adaboost模型对随机项d1进行预测时的网络输入为相空间重构得到的7维数据，输出为1维高程数据，隐含层节点数为8，网络拓扑结构为7-8-1。d2和d3序列的关联维和嵌入维如表1所示。同理，随机项d2和d3可通过相同方法得到预测值。

表1 随机序列的嵌入维和关联维

最后将趋势项序列和3个随机项序列的预测结果叠加，得到组合模型预测值。为验证组合模型的预测效果，采用GA-KF模型(方案1)、相空间重构BP-Adaboost模型(方案2)进行预测, 与本文组合模型(方案3)预测结果进行对比，结果见表2(预测值及其残差)，各方案预测值和实际值对比如图4所示。

表2 各模型计算结果对比

图4 建模序列长度为100期的预测结果Fig.4 Prediction results of modeling sequencelength with 100

由表2可知，方案1和方案2的预测残差较大，其中方案1有3期残差序列绝对值超过1 mm，最大残差达到-1.534 mm；方案2有2期残差序列绝对值超过1mm，最大残差达到-1.774mm；而方案3各期残差序列绝对值均小于1 mm，最大残差仅为-0.479 mm。表明本文组合模型的预测精度相较于其他两种模型有大幅提升。

由图4可以看出，方案3的一步预测值在整体变化趋势上更接近实测值，且每一期的相对误差均小于方案1和方案2，最大相对误差仅为0.002%；而方案1和方案2的最大相对误差分别为0.006%和0.007%，说明方案3综合了单一GA-KF模型和BP-Adaboost模型的优点，可实现优势互补，能更加全面地分析预测复杂数据，预测效果也更加稳定。

2.2 原始沉降序列长度对建模预测结果的影响

为验证不同模型的预测精度是否与原始建模序列长度有关，分别选取最后5期数据的前50、150、200、300期数据建模，对其进行预测。按照上述同样方法，分别使用3种方案对不同长度的沉降序列进行预测，结果见图5和图6。

图5 不同长度沉降序列建模预测结果Fig.5 Modeling prediction results of subsidence sequences with different lengths

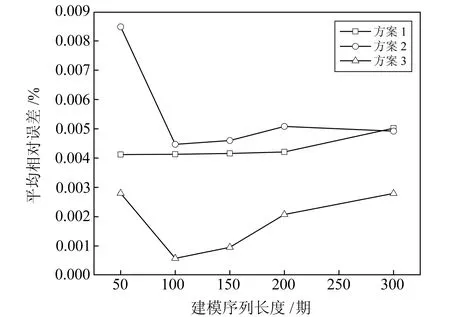
图6 不同建模序列长度下各模型预测误差Fig.6 Prediction errors of each models with different sequence lengths

由图5和图6可知，不同模型的预测精度与原始建模序列长度有一定关系，其中BP-Adaboost模型受影响最大，在序列长度为50期时精度最差，平均相对误差和残差平均值分别为0.008 5%和2.020 mm；当建模序列为100期时，平均相对误差和残差平均值降为0.004 5%和1.065 mm，此时预测精度最好；此后增加序列长度，预测效果逐渐降低，但降低幅度相对较小。GA-KF模型受建模序列长度影响相对较小，但总体预测精度较低，随着序列长度增加，其预测精度并未显著提升，且待预测位置与最开始位置数据的相关性会逐渐减弱，以至于在序列长度为300期时精度变低。本文组合模型受其他两种模型影响，建模序列长度为50期时精度最差，平均相对误差和残差平均值为0.003 0%和0.667 mm；在建模序列长度为100期时精度最高，平均相对误差和残差平均值降为0.000 6%和0.132 mm；此后随着建模序列长度增加，预测精度也小幅度降低，但相比于其他两种模型，该组合模型受影响程度相对较小，且预测精度较高，平均相对误差保持在0.003%以内，远小于其他两种模型。由此可见，本文提出的矿区地表下沉预测模型，抗干扰能力强，预测效果稳定，在实际工程中，可以合理选择建模序列长度，无需持续增加数据量，否则会导致计算效率变低，甚至影响预测精度。

为进一步比较3种模型的预测精度，采用平均绝对误差(MAE)、均方根误差(RMSE)对不同建模序列长度预报结果的精度进行统计分析(表3，单位mm)。

表3 各模型精度对比

由表3可知，对于不同建模序列长度，本文提出的组合模型预测效果均优于其他两种模型，在序列长度为100期时效果最好，相比于GA-KF模型和相空间重构BP-Adaboost模型，MAE分别降低0.847 mm和0.927 mm，RMSE分别降低0.852 mm和1.303 mm。由此可知，通过小波分析充分挖掘沉降数据中复杂的变化特征，采用GA-KF模型预测趋势序列以及相空间重构BP-Adaboost模型预测随机序列可以更好地提取各子序列的沉降信息，有效提高预测精度，对矿区GNSS监测数据具有较强的适应性及稳定的预测能力。

3 结 语

针对传统预测模型的单一性，本文提出地表下沉组合预测模型。通过实验分析，得出以下结论：

1)利用遗传算法对卡尔曼滤波进行优化，得到GA-KF预测模型，可有效克服噪声矩阵难以直接确定的缺陷，对剔除大部分干扰的趋势项进行单步预测；同时考虑随机项的混沌特性，构建相空间重构BP-Adaboost预测模型对随机项进行预测，最后得到的组合模型可综合单一模型的优势，具有更好的预测效果。

2)通过分析发现，不同长度监测序列建模的预测效果不同，本文构建的组合模型具有一定的抗干扰能力，受影响较小，在建模序列长度为100期时精度最高，平均绝对误差仅为0.138 mm，均方根误差为0.223 mm，远小于其他两种预测模型。