新能源示范城市政策对企业绿色创新影响研究——基于我国A股上市公司样本的PSM-DID分析

彭 顺

(重庆工商大学 长江上游经济研究中心，重庆 400067)

一、引言

为应对日益凸显的环境污染和国际碳减排压力，我国开始放弃以“高能耗、高污染、高排放”为特征的传统发展方式，积极探索可再生能源的创新发展模式。自2007年始，我国陆续出台了《可再生能源中长期发展规划》《可再生能源发展“十二五”规划》，对新能源发展进行了部署。2012年国家能源局发布了《关于申报新能源示范城市和产业园区的通知》，正式启动新能源示范城市和产业园区的申报工作。继而2014年国家能源局发布《关于公布创建新能源示范城市(产业园区)名单(第一批)的通知》，确定了81个城市和8个产业园区为第一批创建新能源示范城市和产业园区。

企业作为实体单位，在新能源示范城市建设过程中发挥着重要作用。企业在新能源发电、建造5G基站、组建大数据中心等过程中的创新研发活动无疑为新能源高质量发展和城市能源转型注入了强大的动力。而能源转型不是一蹴而就的，为稳步发展、稳中向前，需要对新能源示范城市可再生能源发展政策(以下简称新能源示范城市政策)影响下的企业绿色创新潜力进行深入评估，以加强企业绿色创新与新能源示范城市政策的有效衔接，促进可再生能源健康持续发展。

在此背景下，本文拟在新能源示范城市这一“准自然实验”条件下，采用倾向得分匹配模型(PSM)与双重差分法(DID)相结合的方法评估企业的绿色创新潜力，即研究新能源示范城市政策对企业绿色创新影响的大小、机制和时效，以及异质性企业对政策的处置效应。本研究对于新能源示范城市进一步建设和发展具有一定的指导意义，同时为后续新能源示范城市的政策制定提供借鉴与参考。

二、文献综述

可再生能源发展政策属于一种环境规制政策。环境规制最早来源于经济学原理的市场失灵外部性理论。新古典学派代表Pigou[1]将“外部经济”进一步扩展为“外部经济”与“外部不经济”，提出了“庇古税”，即通过补贴或征税来应对环境外部性，此为政府干预型环境规制；Eskeland和Jimenez[2]将政府的环境规制进一步划分为市场激励型、命令控制型以及资源协议或环境认证等形式的“软”手段监管型。此后对环境规制的分类研究则绕不开这三种类型。相对于命令控制型，市场激励型环境规制往往被视为更加灵活的监管方式[3-4]，具有以下几种优势：一是具有市场化信息成本节约优势与长期激励减污技术发展优势[5]；二是使企业的创新灵活性增加、生产力提高[6]；三是使企业和产业的边际减排成本相等[7]。新能源示范城市政策兼有市场激励(自愿申请)与命令控制(排放约束)两种类型环境规制的特点，而企业对环境监管的主动自愿行为则属于“软”手段监管型。

近些年国内外学者热衷于研究环境规制对企业绿色创新的影响。Johnstone等[8]研究发现，可交易能源许可证制度有助于诱发与化石能源直接竞争的行业的技术创新；Calel和Dechezleprêtre[9]检验了欧盟排放交易体系对企业技术变化的影响，结果发现对企业低碳技术的促进作用水平大约为10%；Weiss和Anisimova[10]对瑞典高污染行业企业开展实证检验，结果显示，灵活的命令控制型环境规制和经济激励政策工具能够通过提高能源使用效率显著产生创新补偿效应。钱丽等[11]的研究表明，资源环境约束能够正向影响中国企业绿色创新能力；于连超等[12]发现，环境税能够显著促进企业绿色创新，并呈现滞后性特征；李青原和肖泽华[13]发现，排污收费“倒逼”了企业绿色创新能力，“倒逼”效应体现在外部压力和内部激励上。

基于政策试点的示范城市类环境规制对企业绿色创新影响研究的文献也较为丰富。邓玉萍等[14]研究发现，《万家企业节能低碳行动实施方案》对企业绿色创新有着积极的影响；徐佳和崔静波[15]研究发现，低碳城市政策能够有效促进高碳行业中国有企业和非国有企业的绿色技术创新；钟昌标等[16]评估了低碳试点政策对企业绿色创新的积极促进作用；曹廷求等[17]研究发现，《绿色信贷指引》的实施对企业绿色创新活动具有正向影响，能够促进重污染企业积极进行绿色转型；宋德勇等[18]评估了智慧城市建设促进绿色技术创新的显著程度；金环等[19]研究发现，电商示范城市建设试点能够显著促进企业绿色技术创新，而且对民营企业绿色技术创新的作用更显著。

通过众多文献发现，验证“波特假说”(1)波特假说：环境规制可能会促使企业进行更多的创新活动以减少污染，而这些创新活动会间接地促进企业生产力的提高，从而抵消由环境规制而增加的成本，并且提升企业在市场上的盈利能力和相对竞争力。中环境规制对企业绿色创新的影响近些年已成为研究焦点，对政策试点的深入研究也成为学者新的探索领域，尤其是政策试点与企业绿色创新的关系更是成为研究重点。但是这些研究在使用模型时多以控制变量和增减变量来探讨政策试点的处理效应，未从纵向角度研究其动态效应，也未能深度挖掘效应的持续时间。而且，综观近年文献，尚未发现针对新能源示范城市这一政策试点与企业绿色创新关系的研究。基于此，本文将弥补以上不足，主要贡献如下：第一，采用面板倾向得分匹配模型(PSM)结合双重差分法(DID)，验证新能源示范城市政策试点能否诱发企业绿色创新；第二，以政策时点的纵向视角观察新能源示范城市政策的处理效应，构建政策实施后三期的动态效应模型，以识别新能源示范城市政策对每一期企业绿色创新的效应以及持续期，此处理方法有助于更深入发掘新能源示范城市政策对企业绿色创新的时点纵向影响及相互作用规律；第三，创造性地运用面板分位数结合双重差分法评估企业绿色创新，以数值横向水平估计企业绿色创新能力，用以考察新能源示范城市政策与企业绿色创新之间的定量关系；第四，从所有制、所属行业、四大审计的企业异质性角度，探索新能源示范城市政策对企业绿色创新的影响效应及机制。

三、研究模型与样本

(一)数据来源

本文以2003-2019年A股上市公司为研究对象，其中，剔除了金融保险业上市公司、非正常交易上市公司(包括ST，ST*以及PT)以及相关数据缺失的上市公司。本文数据主要包括两个部分：一是企业创新数据，其中公司发明专利和实用新型专利的专利分类号信息从中国研究数据服务平台(CNRDS)获取；二是公司其他特征数据，其中财务数据主要来源于国泰安数据库。将上述数据匹配后，最终获得11 135个年度观测值。

关于新能源示范城市内企业的识别。借鉴向宽虎和陆铭[20]识别开发区内企业的方法，即如果企业地址信息显示企业位于新能源示范城市内，则将该企业识别为新能源示范城市企业；反之，则为非新能源示范城市企业。

关于政策时点的识别。由于新能源示范城市的创建是2012年申报、2014年公布名单，无法获取每个城市准确的准备时间，只能选定一个统一的政策时点。因此，借鉴评估政策效应的双重差分法的相关文献以及研究新能源示范城市的文献[21-23]，选取政策时点为公布名单的2014年。

(二)PSM样本选取

Rosenbaum和Rubin[24-25]经研究提出了一种通过得分匹配获得“反事实”的估计方法，这种方法直接促成了倾向匹配得分模型(PSM)的产生。在该模型的应用中，首先是尽可能多地找到实验组与对照组之间存在差异的变量，组成匹配变量集，记为X≡(x1，x2，…，xn)，然后将分组变量Treated(0-1)对变量集X进行参数回归，常用回归方式为logit(probit)，具体如式(1)所示：

logit(Treated)=Xβ+ε。

(1)

采用式(1)可得回归系数矩阵β。

通过式(2)可计算出得分值ps。

(2)

式中，Xi代表个体i的匹配变量集。

式(2)的本质是将多维的匹配变量拟合成一个一维且介于[0，1]之间的变量psi，即个体i进入实验组的概率。得到psi后，可以根据特定的匹配方式，将实验组与对照组匹配在一起，最后将实验组与对照组进行对比，以识别出二者之间的差异。

但是该得分方法针对的是截面数据的个体，对于面板数据而言，忽略时间效应显然是不可取的。由此，石大千等[26]在研究中采用了逐期匹配的方法，先将面板数据拆分为n>1期截面数据，依据式(1)和式(2)对每期截面数据中所有匹配变量进行逐期logit(probit)回归，计算出每个个体每期的psi，t；然后分别对每期的psi，t进行匹配，得到每期的匹配样本；最后将每期的样本合并成面板数据。本文将此方法记为PSM-DID。谢申祥等[27]在石大千等人的研究基础上将PSM进一步优化，即将每期截面数据的得分值用等时间权重加权获得一个综合得分值，根据这个综合得分值匹配出合适的个体样本，把这些样本按时间序列组合形成面板数据。本文将此方法记为PSMs-DID。另外，该方法还对特殊变量进行了处理，因为在匹配前后特殊变量必须满足一致性，即同一行业相匹配或者同一企业性质相匹配。

参考Chen等[28]的研究，确定公司规模(Size)、资产收益率(ROA)、资产负债率(Lev)、总资产周转率(ATO)、现金流比率(Cashflow)、托宾Q值(TobinQ)、公司成立年限(FirmAge)为PSM方法的匹配变量。

(三)模型设计

为评估新能源示范城市政策对企业绿色创新的影响，对国家能源局2014年发布的新能源示范城市做一次准自然实验。通过构建试点城市与非试点城市、政策前与政策后的交互项，剔除一些不随个体变化或时间变化的因素，以合理评估新能源示范城市的政策效应。借鉴陈林和伍海军[29]关于双重差分法的研究成果与建议，本文建立如下计量模型：

Yi，t=α+βTreatedi×Timet+∑ρControli，t+λi+σt+ηc+εi，t。

(3)

式中，Yi，t表示试点城市某企业在某年的绿色创新变量，以授权专利等数据表征；Treatedi为试点城市虚拟变量，若某企业为新能源示范城市企业，为“1”，反之为“0”；Timet为新能源示范城市政策实施时间虚拟变量，2014年之后为“1”，之前为“0”；Treatedi×Timet是Treatedi和Timet的交互项，也称did虚拟变量，其系数β正是本文最关心的政策效应；Controli，t是选取的一组控制变量；λi，σt和ηc代表个体、时间以及行业截距项的固定效应；εi，t表示计量模型随机扰动项。

(四)变量描述性分析

表1为各变量描述性统计结果。本文被解释变量为企业绿色专利授权情况，包括企业绿色专利授权量(GrePatNum)与企业绿色专利授权比率(GrePatRat)，以及企业绿色专利授权量(GrePatNum)的替代变量——绿色发明专利授权量(InPatNum)和绿色实用新型专利授权量(UmPatNum)，而且对企业绿色专利授权量作1+N的对数处理。控制变量为公司规模(Size)、资产收益率(ROA)、资产负债率(Lev)、总资产周转率(ATO)、现金流比率(Cashflow)、托宾Q值(TobinQ)、公司成立年限(FirmAge)。其中，公司规模(Size)参照规模经济理论[30-32]选取；公司成立年限(FirmAge)参照组织惯性理论[33]选取；其他5个变量是财务报表中的重要指标，属于被广泛接受的企业绩效衡量标准，代表企业市场价值和资产重置价值之间的关系。依据企业特征并结合样本，选取特殊变量为企业的所有制(SOE)、所属行业(Industry)、四大审计(Big4)，即以是否为国有企业、是否属高能耗行业、是否请四大审计公司进行审计来代表企业的异质性。

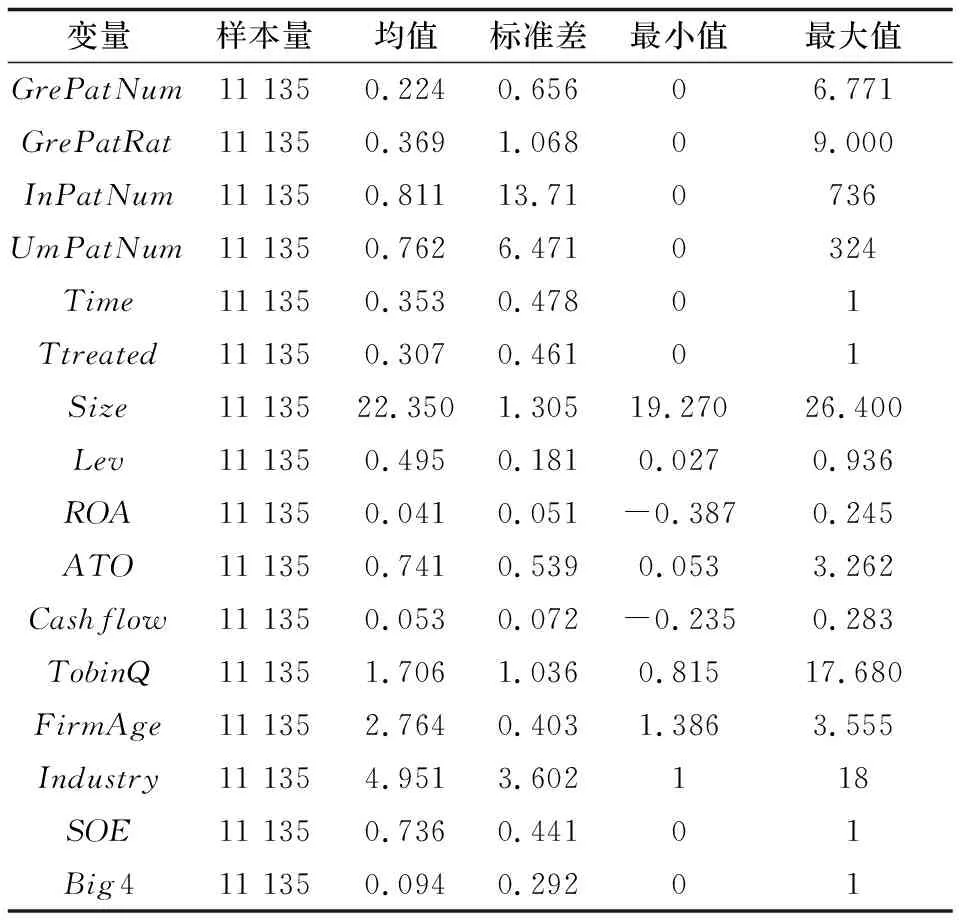
表1 各变量描述性统计结果

四、实证结果分析

(一)政策的唯一性检验

要证明新能源示范城市政策对企业绿色创新具有影响力，根据“反事实”的研究框架，一定要排除掉“非政策时点”与“非政策试点个体”的干扰，由此，必须对政策时点的唯一性与政策试点个体的唯一性逐个进行检验。

1.政策时点的唯一性——平行趋势检验

从政策时点上考量，有效应用双重差分法的重要假设是，如果没有新能源示范城市政策的影响，随着时间推移，实验组和对照组的企业绿色创新变化趋势不具有系统性差异。因此，需要检验平行趋势或者共同趋势的假设是否成立，即检验实验组和对照组的企业绿色创新在政策实施之前必须具有相同的发展趋势。如果不满足这一条件，那么双重差分法得出的政策效应β则不完全是真实的政策效应。

企业绿色专利授权情况的平行趋势如图1所示，横轴表示年度，图1(a)纵轴表示加总到城市层面的企业绿色专利授权量的平均值，图1(b)纵轴则表示企业绿色专利授权比率的平均值，以新能源示范城市名单发布的2014年为政策前与政策后的分界线。在政策前(2003-2014年)，随着年度的变化，对于企业绿色专利授权量均值，其实验组总体略高于对照组，两者的波动大致呈平行趋势；实验组的企业绿色专利授权比率均值与对照组呈现“你追我赶”的波动趋势。在政策后(2014-2018年)，实验组的企业绿色专利授权量均值攀升速度明显加快，与对照组之间的差距逐步拉大；同样，对于绿色专利授权比率均值，其实验组与对照组之间的差距也增大，并且再未出现被“超越”现象。因此，在政策时点2014年之后，确实使原本具有平行趋势的实验组与对照组之间的差距逐渐拉大，双重差分法的平行趋势假说从图形上得到支持。

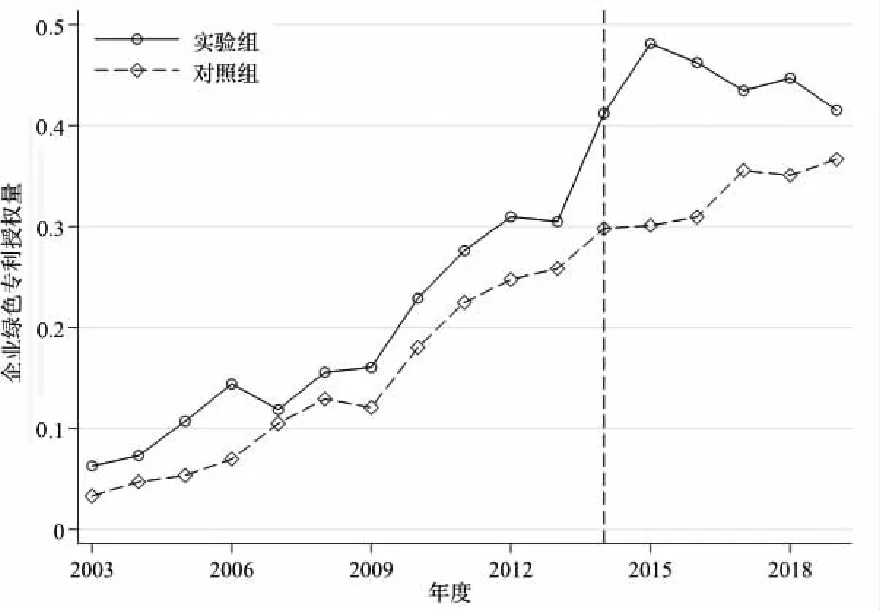
(a)

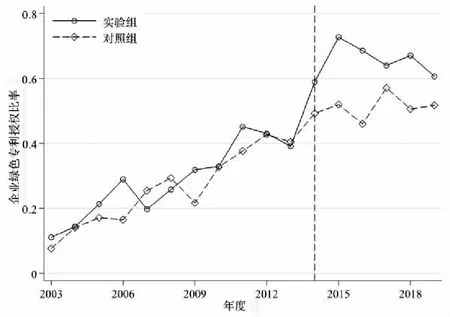
(b)图1 平行趋势检验-时间趋势图

2.政策试点个体的唯一性——安慰剂检验

从政策试点个体上考量，需要证明随着时间的推移，没有依据新能源示范城市名单选择的个体不会出现显著性变化。为避免出现人为的设定，本文采取随机抽样的方式进行实验组的选取。对抽取的样本按照公式(3)进行回归，得到系数β，t值与置信区间；依此重复多次后，得到随机抽样的估计值区间及其分布；最后与原模型的估计值比较差异。这种检验政策试点个体唯一性的方法称为安慰剂检验法。

原模型的估计系数为0.049，t值为2.45。采用1 000次随机抽样，安慰剂检验结果如图2所示。随机数采用的是正态分布函数，大样本下系数均值为0，90%水平下的置信区间为[-1.65，1.65]。从图2中可以看出，实际试点城市样本下的估计值明显异于随机抽样试点个体的结果，原模型稳健性的结果说明政策试点个体具有唯一性，即新能源示范城市名单中试点城市的唯一性得到支持。

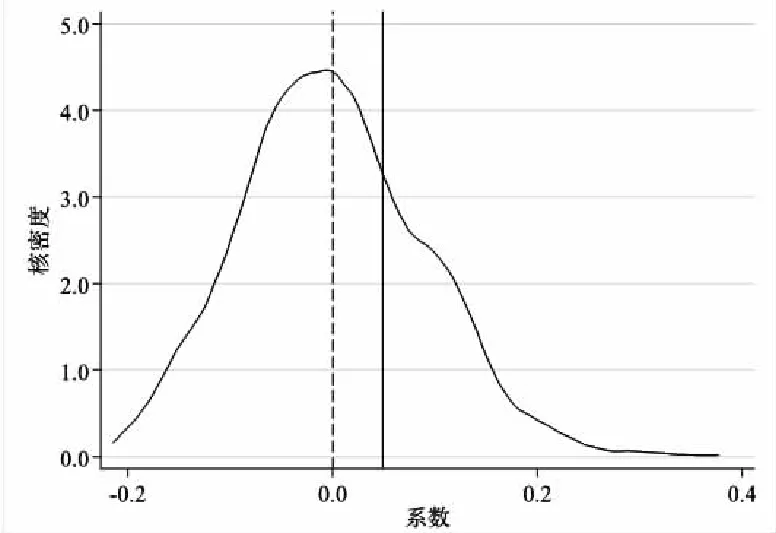
(a)

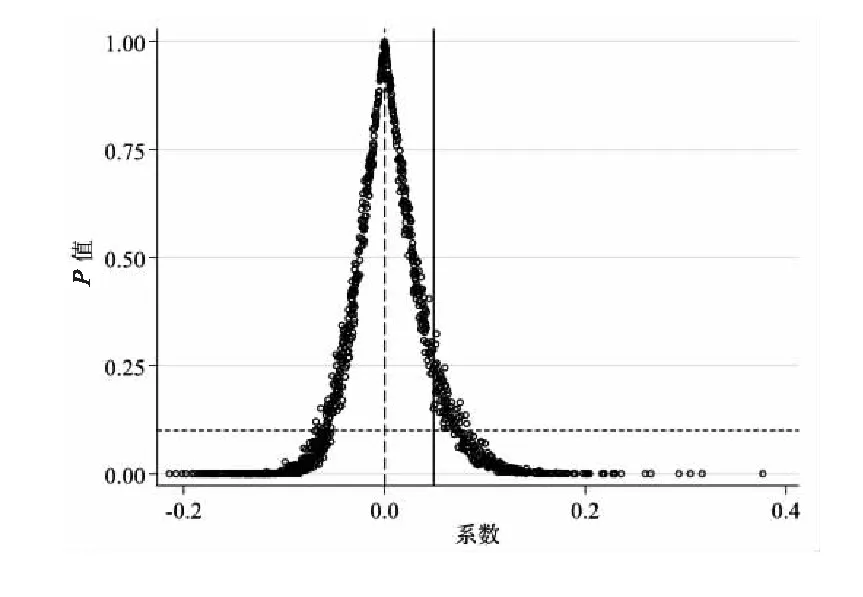
(b)

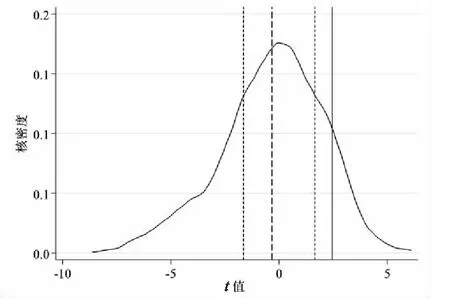
(c)图2 安慰剂检验结果

(二)企业绿色创新的回归结果分析

表2为企业绿色创新的回归结果。第1-2栏为没有进行PSM匹配的回归结果，全样本量为11 135；第3-4栏为参照了石大千等[26]逐期PSM匹配方法的回归结果，通过近邻1∶3匹配将样本量由11 135筛选至8 573；第5-6栏为借鉴了谢申祥等[27]使用的方法先获得逐期得分再以时间权重进行匹配的回归结果，通过近邻1∶3匹配将样本量由11 135筛选至8 409。表2中的模型均采用了Gaure[34]，Guimaraes和Portugal[35]提出的固定效应的回归方法，将个体、时间、行业作为固定截距项。

模型回归结果显示，绿色专利授权量与绿色专利授权比率在DID，PSM-DID，PSMs-DID三个模型中的did系数均大于0，且至少在10%显著性水平上显著。这说明无论是以绿色专利授权量(GrePatNum)衡量的绿色创新绝对水平，还是以绿色专利授权比率(GrePatRat)衡量的绿色创新相对水平，新能源示范城市政策均对试点城市企业绿色创新产生了积极的推动作用。

表2中绿色创新绝对水平模型回归的did系数分别为0.049，0.039，0.040，显著性水平依次为1%，10%，5%，可见PSMs-DID回归结果的大小处于另外两个结果之间。而通过倾向得分匹配方法可知，PSMs-DID将平衡面板数据匹配后依然是平衡面板数据，而PSM-DID匹配后的数据不一定是平衡面板数据，可见PSMs-DID的理论机制准确且结果稳健。因此在后文的回归分析中，主要采用PSMs-DID模型。

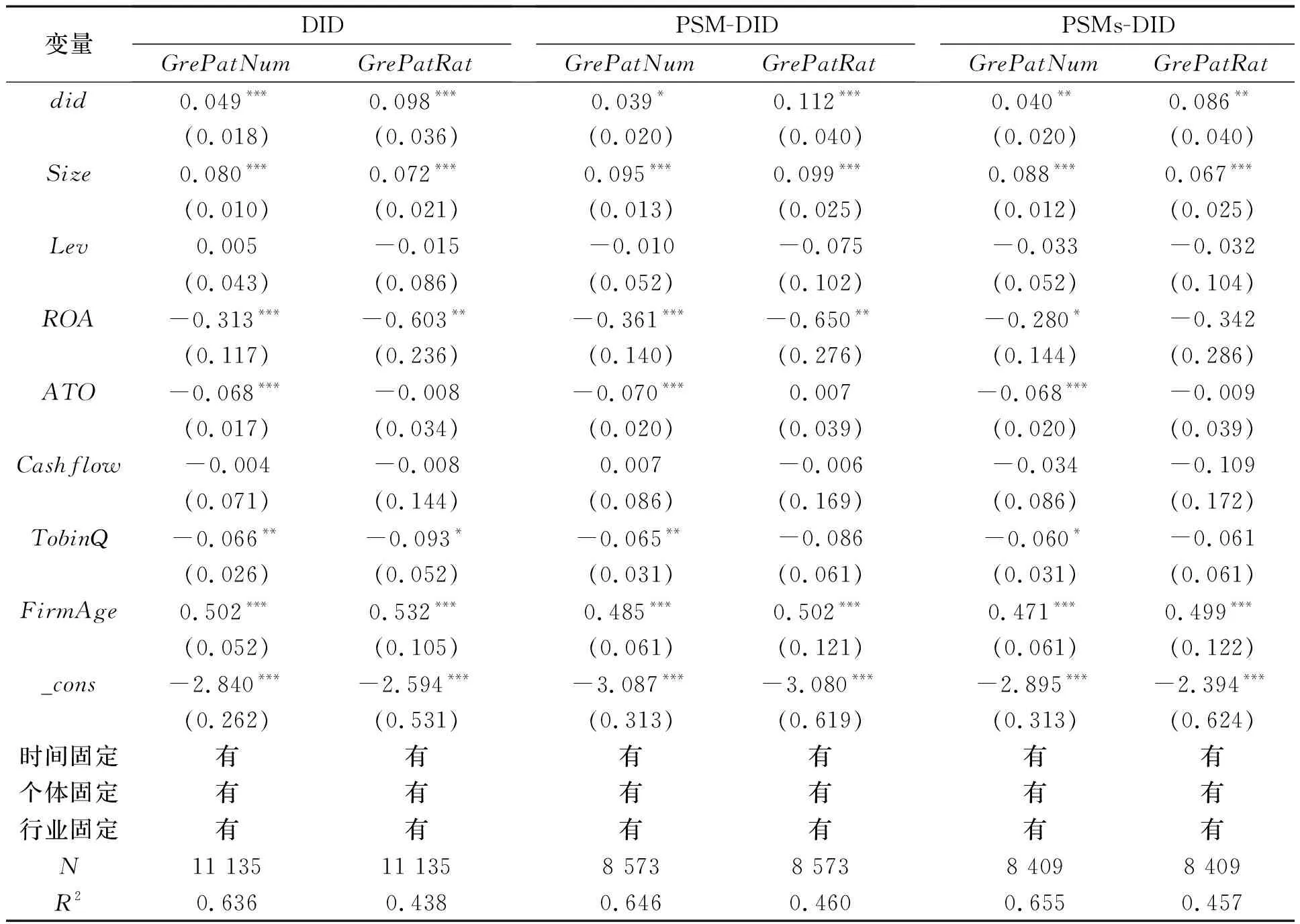
表2 企业绿色创新的回归结果

由表2可知，绿色创新相对水平的回归结果均比绿色创新绝对水平更加稳健，平均显著性水平更高。但是由于知识产权在最近几年得到了进一步保障，专利授权量呈现高速增长趋势，如果用相对水平去衡量绿色创新程度不免会遗漏绿色专利授权的基数及其增加值。而代表绿色创新绝对水平的绿色专利授权量却切实地用到了环境污染的治理中，相较而言，解释力度更高。因此下文以绿色专利授权量(GrePatNum)为主要被解释变量。

为进一步保证回归结果的稳健性，需要考察新能源示范城市政策诱发上市公司企业绿色创新活动的类别。本文以绿色发明专利授权量(InPatNum)和绿色实用新型专利授权量(UmPatNum)作为企业绿色专利授权量的替代变量，来验证不同专利类别的绿色创新水平。为消除异方差，对这两种绿色专利类别变量进行对数处理。

表3为两种绿色专利类别变量的回归结果，其中模型的回归参照了表2中的PSM处理方式与固定个体、时间、行业的回归方法。观察表3可知，在三个模型中绿色发明专利授权量(InPatNum)的did系数都不显著，而绿色实用新型专利授权量(UmPatNum)的did系数都显著。绿色发明专利授权量的did系数在0.01左右，绿色实用新型专利授权量的did系数在0.05左右，比较两者系数可知，绿色实用新型专利授权量比绿色发明专利授权量更受政策的影响。绿色实用新型专利具有研发周期短、消耗资源少和实用性强等特点[36]，而绿色发明专利比绿色实用新型专利的研发周期要长。本文观测的年份为2003-2019年，从新能源示范城市开始创建的2014年至2019年，仅有5年时间，绿色发明专利授权量不显著也能被解释。由此得出结论，新能源示范城市创建后的5年中，新能源示范城市政策主要影响了绿色实用新型专利授权量。

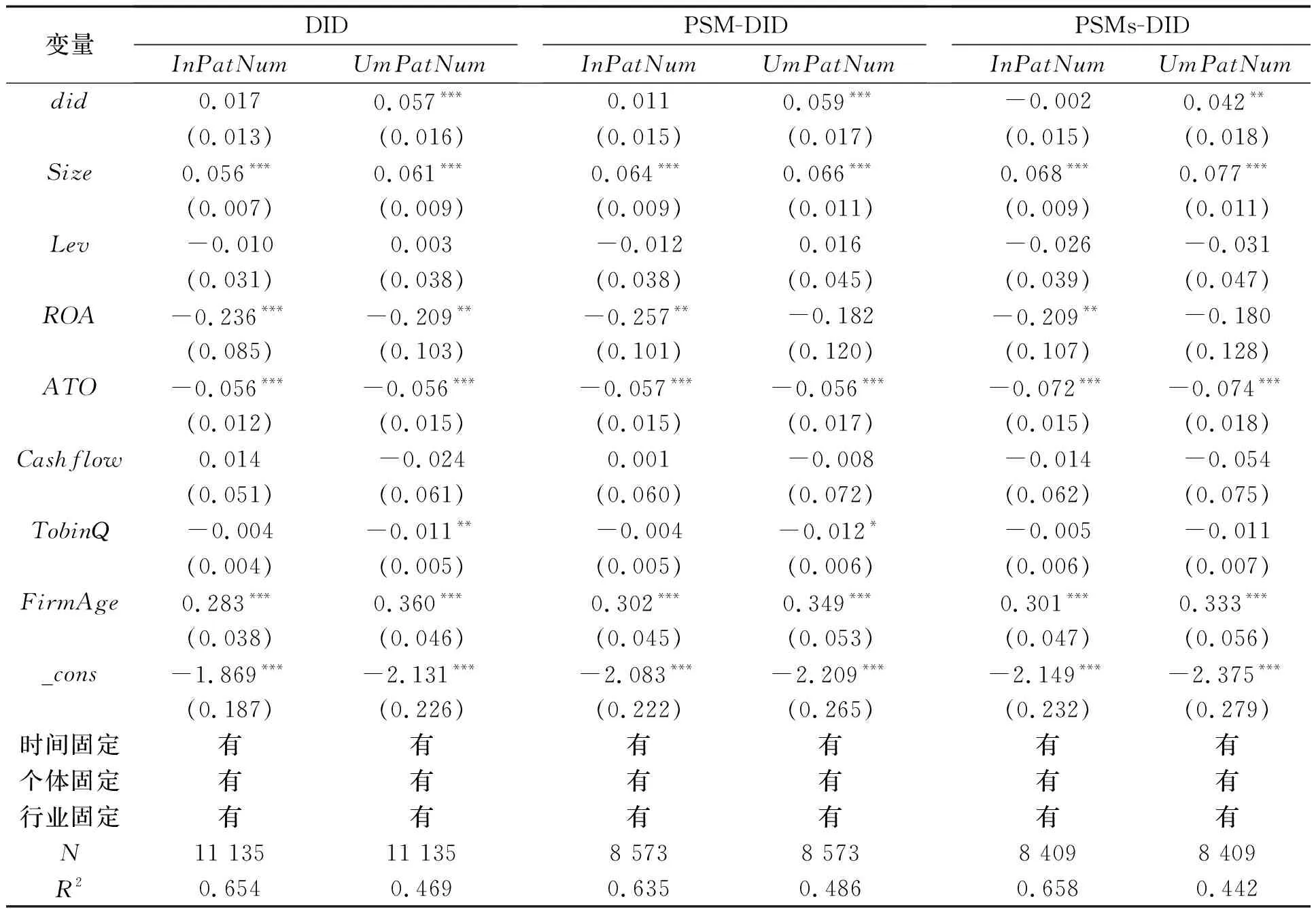
表3 两种绿色专利类别变量的回归结果

(三)政策时点对企业绿色创新的动态效应分析

从纵向维度政策时点上继续考察其对企业绿色创新的动态效应。参照蒋灵多和陆毅[37]的做法，纳入政策时点2014年前的-3，-2，-1期以及2014年后的+1，+2，+3，+4期，生成7个时点虚拟变量，再与Treated变量相乘，生成did虚拟变量，然后将去掉的2014年的时点虚拟变量即0期作为政策效应0值的对照，最后在加入控制变量和固定个体、时间、行业的条件下，分别将企业绿色专利授权量和企业绿色专利授权比率对所有生成的did虚拟变量进行回归。根据回归结果中的did虚拟变量系数画出政策时点的动态效应图，即以直观图的方式呈现新能源示范城市政策在不同年度对企业绿色创新的动态效应，如图3所示。

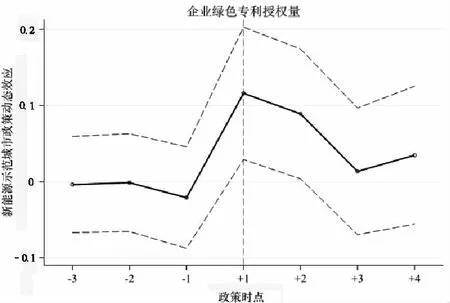
(a)

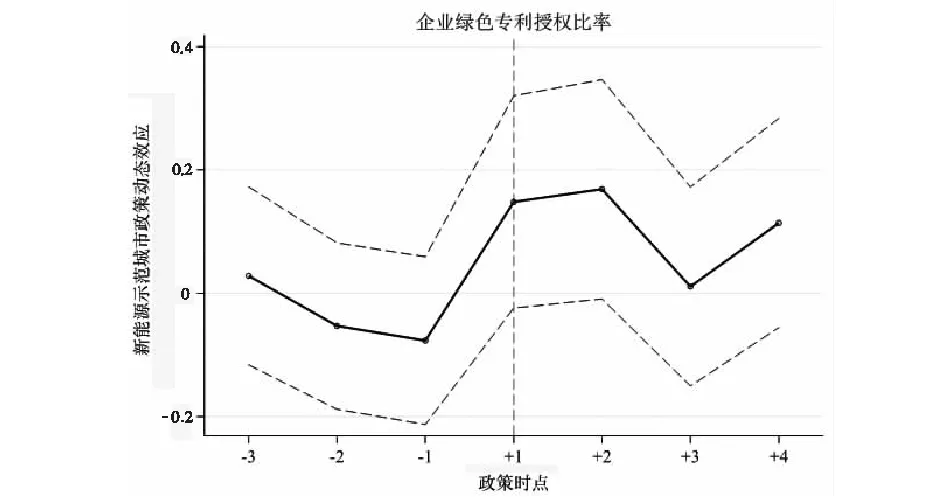
(b)注：实线为did虚拟变量系数，虚线为系数的上下置信区间图3 政策时点的动态效应图

从图3(a)可以看出，对于企业绿色专利授权量，其交互项的系数在政策时点2014年前-3，-2期时几乎为0，-1期时虽不接近于0值，但为负数，说明在政策时点前实验组和对照组之间不存在显著差异，这进一步满足了平行趋势的假设；而在政策时点2014年后+1期时交互项的系数显著为正，随后在+2，+3，+4期时一直保持为正，说明新能源示范城市政策在实施后产生了一个长期的正效应，企业的绿色创新受其长期影响。由图3(b)可以看出，以企业绿色专利授权比率为被解释变量的政策时点动态效果与图3(a)大致相同，并且都表明政策实施后交互项的系数在+2期时开始降低，由此便产生一个疑问：新能源示范城市政策效应的持续期有多长？

为了解答上述疑问，本文借鉴Bernile等[38]研究的冲击的动态效应方法。该研究在分析多期灾难对基金波动性的影响时，对灾难发生前1年与灾难发生后第2年、灾难发生前1年与灾难发生后第3年、灾难发生前1年与灾难发生后第4年三个子样本分别作了多期DID回归，以观察灾难发生对基金波动性的动态效应。依据这种样本处理方法，本文选取2013年与2015年的样本、2013年与2016年的样本、2013年与2017年的样本，分别使用企业绿色专利授权量与企业绿色专利授权比率进行回归，结果如表4所示，其中2013年的样本为政策时点的对照。

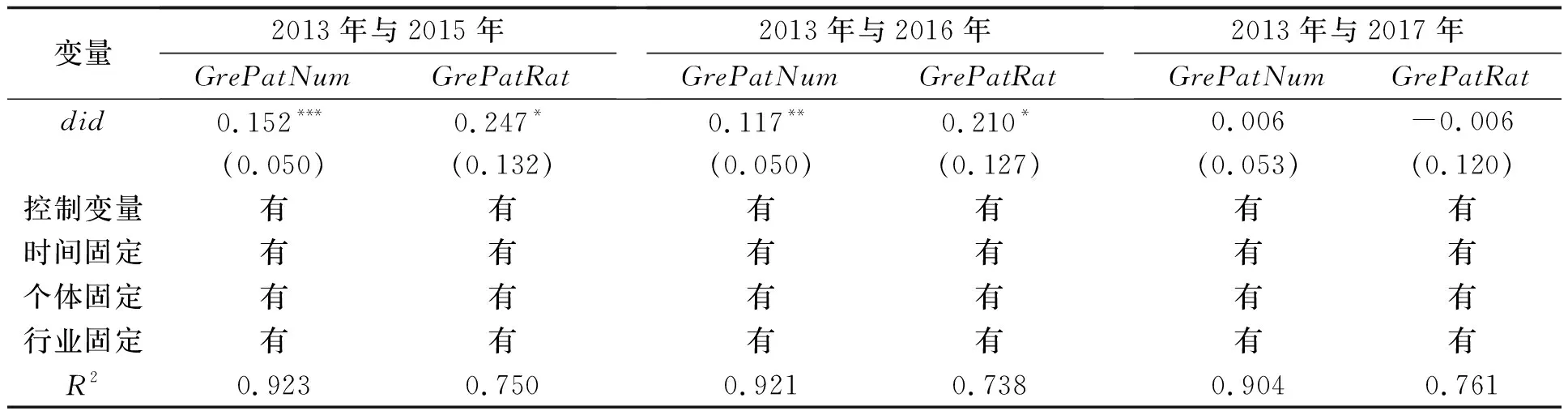
表4 政策对企业绿色创新的动态效应回归结果

由表4可知，政策时点2014年后的企业绿色专利授权量和企业绿色专利授权比率的did系数逐年降低，由政策第2年(2015年)的0.152，0.247下降到政策第3年(2016年)的0.117，0.210，再下降到政策第4年(2017年)的几乎为0且不显著，与对照年份2013年的企业绿色创新水平差异不明显，可见政策对企业绿色创新的影响效应随着时间推移不断降低，并且在第4年几乎消失，说明政策效应的持续期大致为3年。

(四)企业绿色专利授权量的分位数回归

在研究政策效应纵向时点维度的基础上，本文对政策效应的横向维度即绿色专利授权量的大小进行研究。不同水平的绿色专利授权量对新能源示范城市政策有着怎样的反应？本文通过构建面板分位数的计量模型并采用Machado和Silva[39]提出的面板分位数估计方法来解释这个问题，模型如下：

Qv(τ|xi.t)=αi+β(τ)Treatedi×Timet+∑ρ(τ)Controli.t+εi.t。

(4)

式中，Qv(τ|xi.t)为绿色专利授权量的τ分位数，αi为截距项，β(τ)为did的τ分位的系数，ρ(τ)为控制变量的τ分位的系数，εi.t为随机扰动项。

在处理样本时，由于绿色专利授权量的0值较多，故采用严格的1∶1近邻逐期PSM方法对绿色专利授权量为0值的样本进行匹配，最终获得0值的样本量为3 000，大于0值的样本量为1 700。显然这些数据不能获得全分位的分位数，只能从0.6分位开始，每0.1作为一个分位点。

不同绿色专利授权量水平下的企业绿色创新面板分位数回归结果如表5所示。在控制变量、个体固定的条件下，企业绿色专利授权量的did系数从0.6分位数至0.9分位数逐渐增加，并且显著性水平也有逐渐显著的趋势。这进一步说明了回归结果的稳健性，即在不同分位数下，did系数的正负、政策效应的影响方向均未发生变化。

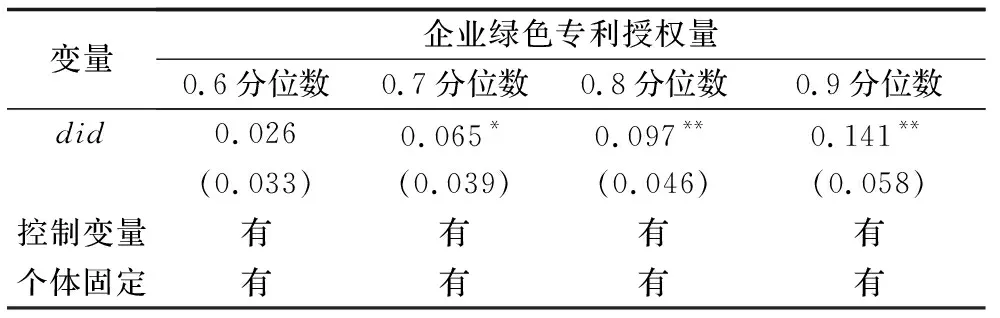
表5 企业绿色创新面板分位数回归结果

为了使面板分位数在采用分位数回归方法时，自变量分组数值能够跟随因变量分组而发生变化，故将政策虚拟变量did与企业变量交叉相乘组成交互项，来检验政策对企业变量的调节效应。选取企业规模(Size)、现金流比率(Cashflow)、公司成立年限(FirmAge)分别代表企业的发展属性、企业的盈利属性、企业成长属性并与政策虚拟变量did组成交互项，对企业绿色专利授权量的分位数进行回归。

did调节效应的面板分位数回归结果如表6所示。政策虚拟变量did与企业规模(Size)的交互项代表了受到政策冲击的企业其规模对自身绿色创新的影响。观察系数可知，在不同绿色专利授权量分位数下，did×Size的系数保持在0.113左右，可见企业规模对企业绿色创新影响非常稳定，说明对于不同的绿色专利授权量分位数，政策对不同规模的企业的绿色创新影响程度基本相似。在三组面板分位数回归结果中did×Cashflow的系数数值最大，大于1，且从0.6分位数至0.9分位数逐步上升，由1.177上升至1.406，这说明在不同绿色专利授权量分位数下，现金流比率的绿色创新边际效应非常明显，且显著提升。而did×FirmAge的系数在此模型中是负向显著，并且政策试点内企业绿色专利授权量分位数增加，公司成立年限对绿色创新抑制作用却随之下降。可能的原因是：对于2014年后成立的公司，国家对其绿色发展有更高的审核要求，样本本身的偏差导致了负向作用，而当变量达到一定水平，企业年限的正向作用对样本偏差的负向作用会有一定程度的缓解。

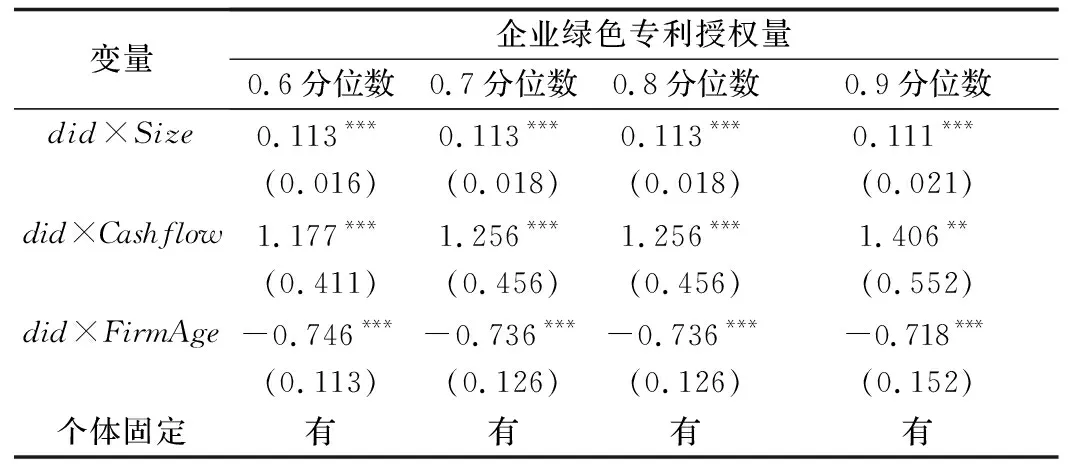
表6 did调节效应的面板分位数回归结果

五、异质性分析

因为表3涉及的三个回归模型中PSMs-DID的回归结果更稳健，所以下文对企业的所有制异质性、所属行业异质性和四大审计异质性的分析仍采用此模型，结果如表7所示。

(一)所有制异质性

国有企业通常会积极响应国家政策，发挥带头作用，同时国有企业获得政策信息的时点一般会早于非国有制企业。因此，下文验证新能源示范城市试点中的国有企业是否在绿色创新中起到了引领作用。具体做法为：首先按照企业所有制类型筛选数据，然后对各个类型的数据进行回归。

表7中第1-2栏分别为非国有企业、国有企业在PSMs-DID中的回归结果。对比这两个结果，发现国有企业did系数为正向显著，而非国有企业为负向不显著。相较于表2中的did系数0.040，表7中国有企业的did系数0.058有明显提升，表明在新能源示范城市政策影响下国有企业在绿色创新中确实起到了带头作用。

(二)所属行业异质性

若某地级市准备申请新能源示范城市或已被确定为新能源示范城市，则这座城市中属于高能耗行业的企业受影响最大，由此可以验证高能耗行业的企业绿色创新的政策效应，并进一步验证政策的实施是否起到了有的放矢的作用。依据高能耗行业的分类，将采矿业，制造业，电力、热力、燃气及水产和供应业，建筑业，交通运输、仓储和邮政业五类行业归为高能耗行业，其他行业为低能耗行业。表7中第3-4栏为低能耗与高能耗行业的企业绿色创新回归结果。对比这两个结果发现，高能耗行业相比低能耗行业，企业绿色创新的贡献度更大。低能耗行业的did系数为10%显著水平负向显著，而高能耗行业为1%显著水平正向显著，可见新能源示范城市政策对高能耗行业的企业确实起到了约束作用，而且新能源示范城市政策的实施具有高度针对性。

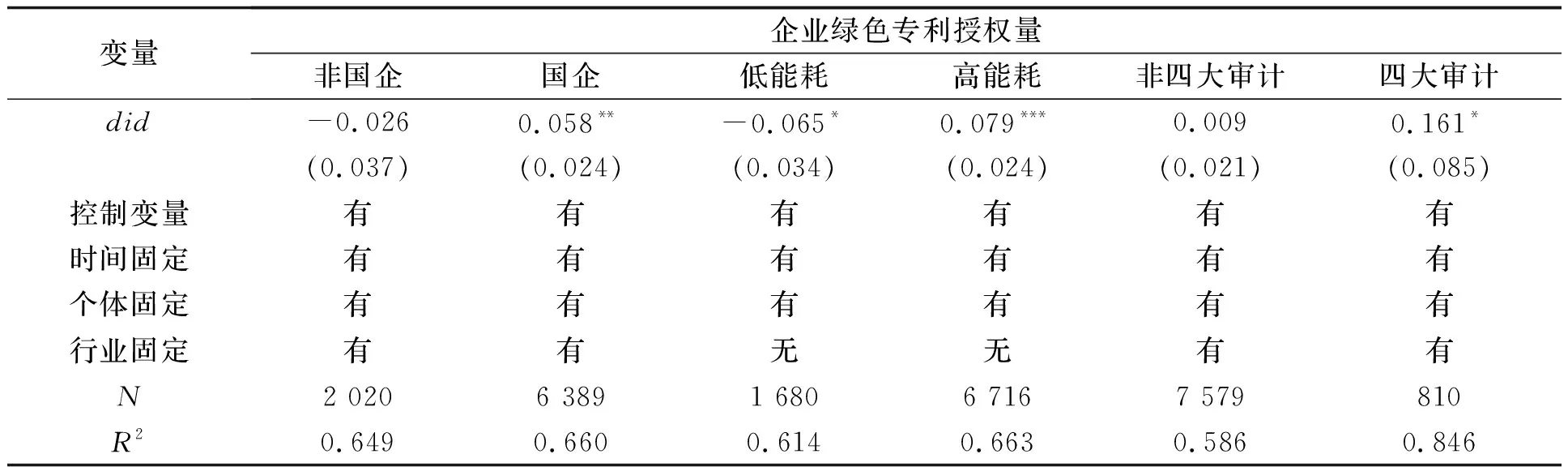
表7 所有制、所属行业、四大审计异质性的回归结果

(三)四大审计异质性

财务状况好的公司会请四大审计公司进行审计，而四大审计公司一般也会审计财务好的公司，这是互为因果的关系。财务状况好的公司是否会主动承担企业责任、积极响应政府号召呢？自2006年中国成为全球第一大碳排放国后，企业的竞争必定是绿色、环保、低碳、生态的竞争已成为共识，谁在这些方面的创新走在前面，谁就有可能在未来立于主导地位。财务状况好的公司有充足的资金担负绿色专利研究的费用，以备公司的长远发展；而财务状况不佳的公司不会有闲置资金去搞绿色研发，更不会邀请四大审计公司进行审计。因此，本文将四大审计作为企业是否有充足资金的指标，而只有在确定企业有闲置资金时，政策的实施是否能有效促进企业绿色创新才能得到进一步验证。

非四大审计与四大审计的回归结果如表7中第5-6栏所示。二者的样本量之比为7 579∶810，然而，样本量少的四大审计企业对绿色创新具有显著性，非四大审计企业不具有显著性。四大审计企业的did系数为0.161，相较于表2中的回归结果0.040，足足增加了3倍。由此进一步得出结论：企业的资金是否充足是影响政策对企业绿色创新产生效应大小的关键因素。

六、结论与对策建议

本文基于2003-2019年我国A股上市公司的面板数据，采用倾向得分匹配模型(PSM)和双重差分法(DID)相结合的方法，检验评估了新能源示范城市政策对企业绿色创新的影响效应，研究结论如下。第一，新能源示范城市政策诱发了试点城市内企业绿色创新行为，企业绿色创新绝对水平和相对水平显著提升。第二，从绿色专利类别来看，相对于绿色发明专利，新能源示范城市政策更显著影响企业对绿色实用新型专利的研发。第三，新能源示范城市政策在其实施的第4年(2017年)对企业绿色创新的政策效应几乎减弱为零，说明政策效应的持续期大致为3年。第四，在企业绿色专利授权量的0.6分位数至0.9分位数的水平下，政策效应did系数随着分位数的增大而显著增大。在企业调节变量的政策效应中，企业发展属性(企业规模)的did系数较为稳定，而企业盈利属性(现金流比率)的did系数值最大，且随分位数的增大而升高，是企业绿色创新的重要影响因素。第五，国有企业比非国有企业研发创新更加积极，新能源示范城市政策对前者影响更显著；高能耗行业的企业受新能源示范城市政策的影响比非高能耗行业的企业大，说明新能源示范城市政策非常具有针对性；四大审计企业的政策效应did系数比非四大审计企业大，说明企业的资金充足是影响政策对企业绿色创新产生效应的关键因素。

基于上述结论，本文提出如下对策建议：首先，新能源示范城市政策对企业绿色创新活动具有正向促进作用，表明推行新能源示范城市政策符合我国可再生能源的发展策略，因此，政府可以考虑进一步扩大新能源示范城市政策的实施范围，贯彻“绿水青山就是金山银山”的新时代绿色发展理念；其次，新能源示范城市应鼓励企业加大对绿色发明专利的研发投入，长期的环境治理必须依靠绿色发明专利与绿色实用新型专利的支持，而研发投入是绿色创新的基本动力，对此政府也应给予适当补贴，以便更加有效推动企业的自主创新；再次，新能源示范城市的企业绿色创新热度维持在3年左右，故应以3年为一个周期做好新能源示范城市政策的宣传工作，使政策效应更持久；最后，对于不同类型的企业，地方政府应因“类”制宜地制定环境规制政策。