基于卷积神经网络的多模态过程故障检测

王琪善，章国宝*，黄永明，张永春

（1.东南大学 自动化学院，南京 210000；2.江苏省特种设备安全监督检验研究院，南京 2 100018）

0 引言

现代制造业设备的发展呈现出智能化、综合化和复杂化的趋势，系统各设备之间高度耦合，导致维护和保养的成本越来越高，同时某一个设备的故障可能引发连锁反应，引起系统的崩溃，因此降低故障的误报和漏报率对保障系统安全性、降低维护成本，具有重要的价值和意义[1]。传统的多元统计过程控制（MSPC）主要包括主成分分析（Principal Component Analysis，PCA）和偏最小二乘（Partial Least-Regression，PLS）法[2]，已被广泛用于分析监测数据和故障间潜在的关系，当信号超过阈值或发生显著变化时将触发报警。然而随着工业流程变得复杂，工况更加多变，制造过程呈现出运行模态多样、非高斯分布、非线性变化，故障类型多变等问题，使得故障检测变得更加复杂。

传统PCA和PLS方法根据历史数据的统计信息建立静态模型，将高维变量映射到低维空间进行分析，然而要求数据满足高斯分布和线性特征，在非线性、非高斯的多模态过程中经常产生误报和漏报，效果不佳。对此，许多研究人员提出了改进。为了解决非线性问题，文献[3]使用动态主成分分析方法，生成增广数据矩阵拟合非线性过程特征。文献[4]使用局部近邻标准化改进最小二乘法的非线性表现。文献[5]提出一种结合随机投影和K近邻的故障检测方法，适应了过程非线性的特点，文献[6]提出非负矩阵分解和Fisher判别分析。为了解决非高斯问题，文献[7]结合核PCA和支持向量机（Support Vector Machine,SVM）进行故障检测，数据无需满足高斯分布。文献[8]使用独立主成分分析（ICA）信息融合提取轴承故障特征。为了满足多工况、多模态的故障检测需要，文献[9]针对各个模态使用MSPC单独建模，而非全局建模来容纳所有模态，因而随着模态的增多，计算复杂度较高。文献[10]将贝叶斯统计引入MSPC，通过后验概率和联合概率评估检测统计量在各模态下的故障概率。文献[11]将局部熵引入ICA，将监测数据转化到局部熵空间，以提高多模态和非高斯过程检测效果。

总体来说，由于上述监测方法的阈值和置信度是通过统计方式获得，因此性能会受到基于MPSC方法设计参数选择的显著影响。因此，在解决非线性、非高斯的多模态过程故障检测问题上，MSPC方法首先较易忽略原始模式数据中的某些潜在关系，因而不能涵盖对早期微小故障的准确检测[12]。此外，MPSC方法还会因变量间的耦合而产生意料之外的误报和漏报。

近年来，通过将故障检测视为一个判别性问题，人工智能技术已在该领域得到了成功的应用[13]。如果原始测量数据的潜在关系可以通过合适的学习算法来学习，则可以很容易地识别模式的从属关系。对于高维工业制造数据，可以有效地使用深层结构来发现低层特征固有的模式，从而提高分类准确性。Hinton等人[14]提出了反向传播算法，使得深层结构的参数更新和高级抽象特征的获取成为可能，其较强的学习能力强，适用于多模态过程的故障检测。作为一种深度学习方法，CNN已证明其在各个领域如语音、图像等多元模式识别中的功效[15]。其主要的优势体现在：

1）以卷积加采样为核心的网络结构可以直接提取信号中的局部特征，不需要手动提取；

2）随着网络堆叠层次的加深，模型可以获得更好的能力来表征数据和设备健康状况之间复杂的（线性或非线性）映射关系，从而提高判别能力；

3）数据不要求必须满足高斯分布。在多模态过程故障检测领域，基于CNN的深度学习判别方法方兴未艾。文献[16]将数值数据表示成雷达图，然后将其输入CNN中构建分类模型，取得了优异的故障检测效果，然而同文献，每个模态单独建模将导致复杂性的增加。文献[17]使用轻量级CNN提取多变量过程的高层特征，在测试集上提高了8%的故障检测率，然而在将传感器数值转换成图像的过程中没有考虑变量的相关性。文献[18]使用固定多重采样CNN提取过程数据在不同时间尺度上的动态特性用于故障检测，然而没有对模型提出进一步的优化。

为此，本文提出了一种基于TCNN的多模态过程故障检测方法，提出了基于TCNN的在线监测框架，建立关于多模态过程的全局判别模型，可以进行实时的模态识别和故障检测。与常规的MSPC方法不同，TCNN的非线性激活函数和模型结构适用非高斯分布和非线性特征，深层的模型能够拟合更深层次的结构信息和数据本质，提高了对多模态过程故障的检测效果。最后将提出的方法用于田纳西伊士曼工业过程(Tennessee Eastman Process,TEP)的故障检测中，与MSPC（PCA）方法，SVM方法、深度置信网络（Deep Belief Networks,DBN）方法进行了实验比较，结果表明本文提出的方法总体上降低了故障的误报和漏报率。

1 Tiled CNN

1.1 判别模型结构

Tiled CNN（TCNN）是卷积神经网络的一种变体，使用卷积和多个特征图来学习不变特征。其特殊性表现为本地连接和平铺（tiled）权重共享，即使用参数k控制隐藏层的权重绑定距离，能够学习平移不变性之外的复杂不变性（如尺度不变性和旋转不变性）,更适用于复杂不变特征的学习。该模型由多个卷积和TICA采样层堆叠而成，如图1所示。卷积在局部感受野提取多个特征图，作为TICA采样层的输入。TICA采样可从未标记的图像块中学习特征，结构如图2所示,由两层网络构成，分别具有平方和平方根非线性采样功能，详细介绍参见文献[19]。

图1 TCNN网络结构

图2 TICA层结构

1.2 判别模型训练

给定一组训练样本X={x1,x2,x3,...,xk},由未标记的多模态过程测量值构成某一模式矩阵，xi=k为采样点个数，n为传感器个数，系统的模式即隐藏在矩阵之中。由于高维模式识别属于非线性可分离问题，因而可以转换为学习一个可将特征映射到特定模式的函数，然后将模式与其相应类别进行匹配。对于本文的模型结构来说，即学习非线性函数以提取表征故障模式的高层矩阵特征X=FW,b,k(X)。FW,b,k模型的训练分为TICA无监督预训练和有监督微调两部分。无监督预训练阶段，通过硬编码固定第二采样层的权重V来学习第一层中的权重W，即解决：

其中，x(t)为经卷积后输入的局部特征，n是输入大小，m是隐藏层单元个数。有监督微调阶段使用softmax回归计算梯度，将误差从输出端进行反向传播（BP）逐步更新权重。给定不同模态下的有标签数据集其中k为模态的个数，为了计算给定假设函数：

1.3 基于灰狼优化算法的超参数寻优

超参数的选择对模型的训练速度和最终的分类效果具有重要的影响。目前没有成熟的理论指导选择超参数的值，通过反复试验手动进行调整是一项耗时的工作。本文使用灰狼优化（WGO）群智能启发式搜索算法[20]进行超参数寻优，以期获得最佳的多模态分类模型。灰狼优化技术模仿了狼群寻找猎物位置的行为。从最初的随机分配开始，狼的位置会进行迭代更新，以将其引导至猎物即最佳解决方案附近。在狩猎中，狼群采用α,β,δ,ω四层机制按顺序搜索猎物，分别被称为最佳、第二佳、第三佳和其他解决方案。对于本文，每只狼的位置都与CNN模型超参数的个数相对应而构成一个矢量Xi={Xi1,Xi2,...XiD}，D为搜索空间，即超参数的个数。x={X1,X2,...XN},N为灰狼的数量，那么α,β,δ狼各一只，ω狼有N-3只。在更新位置之前，每只狼首先计算自己和α,β,δ狼的距离：

其中D表示距离，X表示位置，r为随机数。随后每只狼按照以下的公式更新自己的位置：

其次，超参数寻优的目的是提高分类准确度，因而定义灰狼适应性函数为：

本文基于灰狼优化的TCNN模型超参数寻优算法，见算法1。

算法的时间复杂度为O(itermax*N*t)，itermax为迭代次数，N为灰狼个数，t为TCNN一次前向计算的时间。

2 传感器数据图像编码

将多维传感器监测数据转换成图像，是预处理步骤的核心问题。为了满足在线实时检测同时充分保留传感器数据特点的需求，本文提出基于格拉姆矩阵的差值图像编码方式，易于实施且不丢失原始数据的特征。在时间点t，工业现场采集到的多维传感器数据V={v1,v1,...vm}，其中vi表示第i个传感器的数值，m是传感器的数量。首先使用z-scores[21]将数据归一化，避免不同量纲带来的影响。定义vi,j为两个不同的传感器数据的差值，即vi,j=vi-vj,i≠j。定义格拉姆差值矩阵G如下：

可以看出，格拉姆矩阵的主对角线保留了原始的传感器数据，即Gii=vi。而每一行保留了每个传感器和其他传感器的数据差值特征，即Gij=vi,j，当模态的变化或故障的发生表现为某些传感器数值的变化时，这可以在矩阵的差值特征中表现出来。为了将矩阵转化成图像，可以按照公式进行缩放：

其中Gmax,Gmin分别为G中的最大值和最小值，I为单位矩阵。图3(a)展示了52个传感器在两个不同采样时刻的采样值，分别标为红色和蓝色。通过差值编码后对应的图像为图3(b)和图3(c)。可以看出两个时刻传感器数据的变化在图像上表现为不同的局部特征，为模态的辨识和故障的检测提供了基础。

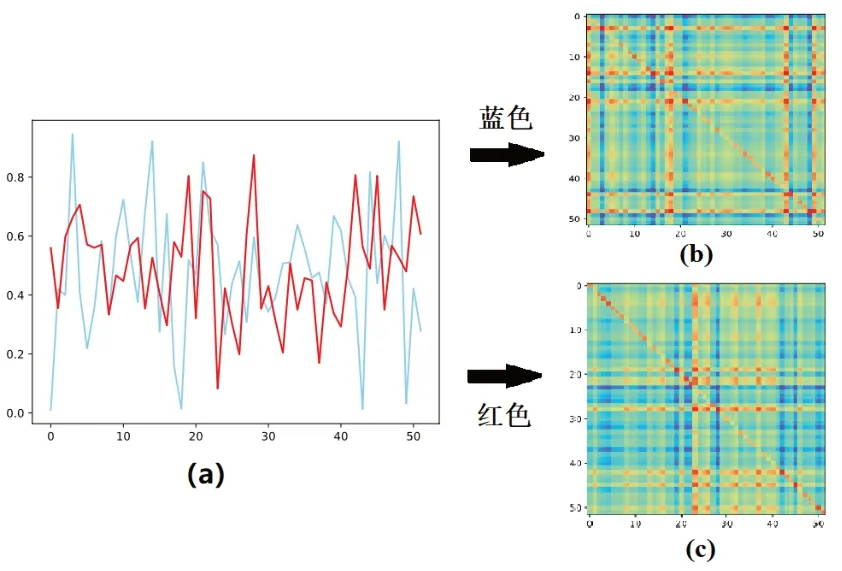
图3 插值编码

3 基于TCNN的多模态过程在线监测方法

基于TCNN的多模态过程在线监测方法的框架如图4所示。首先基于历史数据进行离线的模型训练，数据经过编码之后构成数据集用于训练TCNN，通过灰狼优化进行超参数寻优以期获得较优的分类模型。在线阶段使用训练好的模型提取在线数据的高层特征识别当前运行的模态，进一步通过离线学习到的模式匹配当前运行状况。

图4 TCNN在线监测框架

与传统的MSPC方法不同，本文方法通过深层模型学习数据深层的特征，减少信息的丢失且不容易受到变量耦合的影响，以期提高在线监测的效果。

4 TE过程实验验证

4.1 数据集介绍

本节以公开标准化工过程TEP数据集进行实验。TEP过程由美国某化工公司控制部门提出，由反应器、冷凝器、分离器、循环压缩机和汽提塔五个单元构成，系统中有52个传感器遍布管道、阀门和各种子设备进行变量监测，其运行结构如图5所示，过程输入反应物料为A,C,D,E四种，生成物料有G,H,F三种。本文使用41种测量值，包括22个连续测量值和19个成分变量，采样间隔为3分钟。TEP过程有多种运行模态，每种运行模态都包含1种正常情况和21种故障情况。训练集每种情况包含480个样本，共计10560个样本。测试集每一类故障包含960个样本，故障是在第160个样本引入，共计17600个样本。

图5 TEP过程流程图

4.2 模型离线训练

本文选择了TEP的基本模态、模态1、模态3和模态4的历史数据训练模型。各个模态的工艺参数如表1所示。

表1 TEP模态参数

总数据集数量为10560*4=42252个。使用Keras框架搭建TCNN模型结构为:输入层、卷积层*4、TICA采样层*4、全连接层*1。初始化灰狼个数为50，迭代次数设置为50，初始权重采用随机初始化方法并进行三次实验。实验环境为Intel i7,GPU 2080 Ti。三次实验结果如图6所示。

图6 三次优化实验结果

模型超参数选择第三次实验的结果，超参数如表2所示。

表2 超参数寻优结果

4.3 工作模态识别

首先验证TCNN网络对工作模态的学习能力。TCNN模型最后学习到的全连接层特征是长度为128的一维向量，在某采样时间点，四种工作模态下的向量值如图7所示（从上到下依次为基本模态，模态1，模态3和模态5）。可以看出，四种模态在该采样时间的特征向量彼此相异，表现为不同的上限和变化特征。

图7 四种模态特征向量值

进一步为了说明TCNN学习到的特征向量对模态的辨别能力，每个模态选取160个正常状态的测试样本进行模式的辨别。分别选取特征向量的第2，4，18和23四个维度上分别进行比较，如图8所示。

图8 四种模态在各个维度上的辨识结果

可以看到，在这四个维度上，四种模态分别在特定的范围内变化，可以和其他模态较好得识别开。基本模态可以通过第18维识别，模态1可以通过第2维识别，模态3可以通过第23维识别，模态5可以通过 第4维识别。作为对比，使用文献[22]的PCA方法，选取TP2和SPE控制限对基本模态进行识别，其在线监测结果如图9所示。可以看出控制限的划分导致较多的漏识别情况。本文所提出的框架，学习到各个模态的特征更直接和清晰，可以起到相对较好的识别效果。

图9 PCA方法对基本模态的识别结果

4.4 故障检测

为了说明所提出的框架在检测故障状态方面的有效性，以基本模态为例，在测试集上进行了20种故障的实验。其中故障13为缓慢漂移故障。对过程的干扰较小因而较难检测，TCNN模型第四层TICA采样后学习到的正常状态特征图和故障13特征图见图10。在特征图上故障13呈现局部亮点的特征，可以和正常状态较好得区分开。

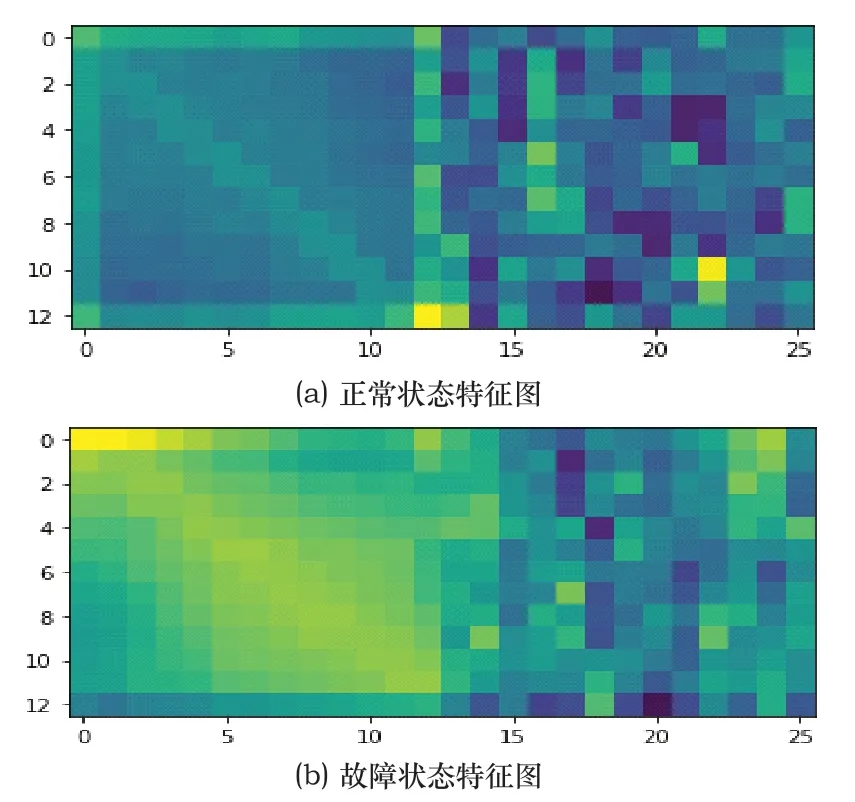
图10 正常和故障13的特征图

在线检测阶段，在基本模态下模拟了24小时的运行状态，在第8个小时引入故障13，本文方法的检测结果如图11所示。图中的异常说明发生了漏报或者误报。正常阶段在4个采样点产生了误报，故障发生后在8个采样点发生了漏报，误报率和漏报率均为2.5%。作为对比，分别使用文献[22]PCA和文献[21]SVM方法,文献[23]DBN方法对故障13进行检测。结果如图12～图14所示。

图11 本文故障13在线监测结果

图12 PCA方法对故障13的监测

图13 SVM方法对故障13的监测

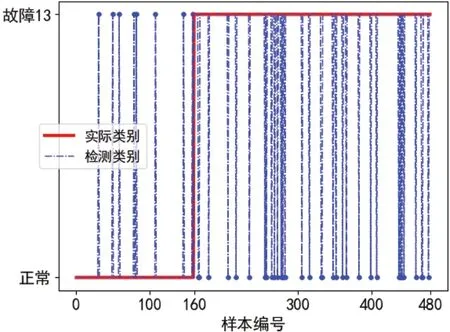
图14 DBN方法对故障13的监测

从图中可以直观得看出PCA方法得漏报和误报率较高，DBN方法优之，SVM方法较优，但都劣于本文方法。在误报率上，上述三个方法分别为12.7%，6.2%和5%，均高于本文的2.5%。在漏报率上，上述方法分别为15.6%，7.5%和10.9%，均高于本文的2.5%。在故障13的综合检测率上，本文方法取得了较好的结果。

接着，在基本模态下所有20种故障的检测率和对比结果如表3所示。

表3 各方法故障监测率对比

表中每类故障最好的检测结果均加粗标出，其中CNN方法取得了14次最好的结果，高于其它方法。同时CNN方法对故障10，16和19的检测率高于其他方法10%以上。此外TCNN方法的平均故障检测率最佳，高出PCA方法11.27%，高出SVM方法1.83%。

5 结语

本文提出了一种基于TCNN的多模态过程故障检测方法，利用差值编码将传感器数值转换成图像，用于训练全局判别模型，使用灰狼优化算法进行超参数寻优。提出的方法可以进行在线的模态识别和故障检测，在TEP数据集的实验结果表明，该方法有较好的模态识别率和故障检测率，降低了误报率和漏报率。该方法为多模态故障智能检测提供了新的思路。