基于机器视觉的直齿轮齿距偏差检测*
逯海滨 张 丹 李长安 隋文涛 窦亚萍 张宇凡
(①山东理工大学机械工程学院,山东 淄博 255049;②山东理工大学电气与电子工程学院,山东 淄博 255049)
齿轮是现代工业生产中最常见的零部件[1],作为现代工业系统的核心零部件,其结构设计水平和加工精度是决定机械产品性能的决定性因素之一。由于齿轮的几何结构复杂,测量参数繁多,测量结果的准确性直接关系到齿轮的制造精度和各种性能,因此,快速、准确地测量和分析齿轮的参数和精度具有重要意义。
齿距偏差是评定齿轮精度的几何元素之一,对其进行齿距偏差检测至关重要。为了避免人为因素对测量结果造成影响,实现齿轮在线测量,提高齿轮齿距偏差测量的准确率,研究人员引入了机器视觉使用非接触测量来代替传统的接触测量[2-4],并取得了一定的进展。文献[5]设计了一种基于机器视觉的齿轮测量系统;但是该系统在面对镜头畸变时无法进行校正,测量精度低。文献[6]搭建的基于机器视觉的齿轮参数测量系统,可以实现各项参数的测量,测量精度可达0.1 mm。文献[7]使用最小二乘法拟合得到了齿顶圆、齿根圆的半径;但该方法会受到轮廓曲线提取效果的影响,造成较大误差。
针对齿距偏差检测中存在的问题,本文以标准直齿轮为对象,研究了基于机器视觉的齿距偏差研究方法。并引入改进的Zernike亚像素边缘检测算法[8-10],测量得到了齿轮的参数,对进一步提高齿距偏差测量准确性及可靠性具有重要的现实意义。
1 测量系统构成及测量流程
1.1 测量系统构成
本文齿轮齿距偏差测量装置[11]如图1所示,主要由CCD工业相机、镜头、环形光源、工作台和计算机等组成。工业相机通过螺栓固定在支架上,其高度通过转动手轮来调节。测量过程中,将待测齿轮放至工作台上,调节相机高度及光源亮度使得拍摄的图像最为清晰,并将采集到的图像传输到计算机上,基于计算机,对采集到的齿轮图像进行处理并测量出齿轮参数。

图1 机器视觉装置构成图
1.2 测量流程
根据齿距偏差测量原理制定测量流程,测量流程图如图2所示。
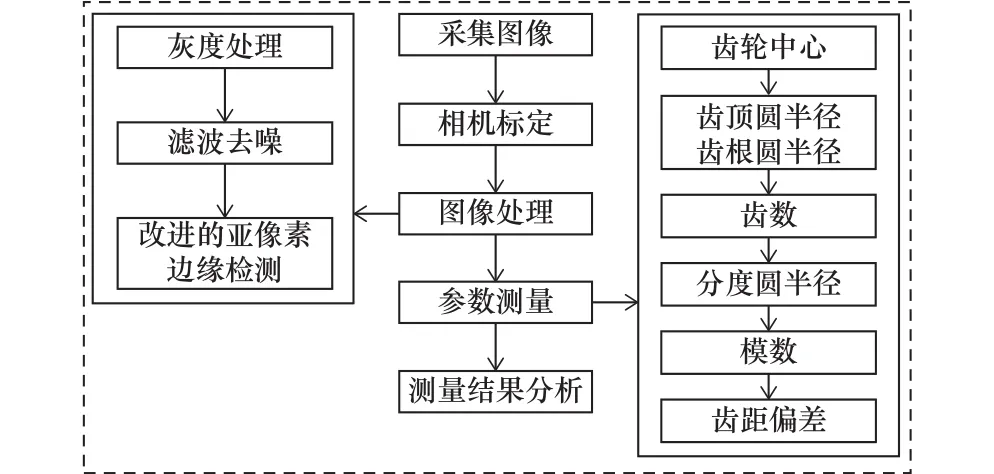
图2 测量流程图
2 相机标定与图像预处理
2.1 畸变校正
为了提升对图像的测量精度,减少镜头畸变的影响,需要对图像进行畸变矫正[12]。本文采用基于张正友法的相机标定[13],畸变校正流程如图3所示。
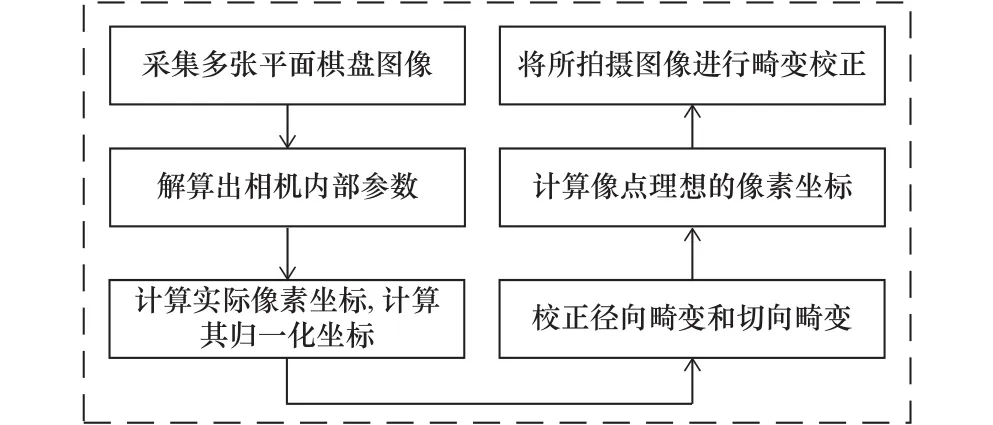
图3 畸变校正流程
在校正过程中,矫正畸变通过泰勒展开式取前3项。径向畸变校正中,畸变通过泰勒级数展开式校正为
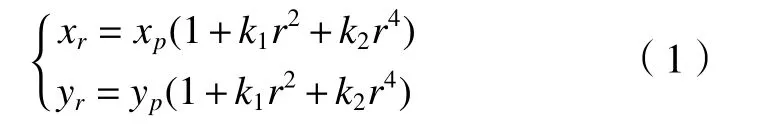
在切向畸变校正中,畸变通过泰勒级数展开式校正为

式中:k1、k2为径向畸变系数;p1、p2为切向畸变系数;(xr,yr)、(xp,yp)为归一化处理的无畸变像点和实际像点坐标;r为无畸变像点坐标与光学中心的距离。
2.2 像素当量标定
测量齿轮齿距偏差的过程中,需要实现像素坐标尺寸到实际尺寸的转换。
使用Harris角点检测算法[14]对校正后的棋盘格进行角点检测,将提取出的角点作为像素当量标定的特征点。通过计算任意两个相邻的同行角点间的物理尺寸和像素数量,得到棋盘格上此行的像素当量,计算多个同行角点的像素当量并取平均值。所得结果即为系统像素当量,测得本系统像素当量:K=0.018 mm/pixel,计算如式(3)所示。

式中:K为系统像素当量;Ki为同行相邻角点的像素当量;S为相邻角点物理尺寸设计值;Pi为相邻角点像素数量。
2.3 图像预处理算法
本文采用工业相机在背景光源照射下采集,待测图像如图4a所示,在获取待测图像后,对图像进行预处理算法,提升待测图像的质量。为提升图像处理速度,对图像进行灰度化处理。

图4 图像预处理结果
为避免噪声干扰对图像质量的影响,改善图像清晰度。本文选择中值滤波对图像进行滤波去噪处理,图像预处理后的灰度图如图4b所示。
3 改进的Zernike矩亚像素边缘检测算法
3.1 Zernike矩边缘检测算法原理
对于离散函数f(x,y),其n阶m次Zernike矩可以定义为

式中:V* n,m(ρ,θ)为核心公式的共轭;ρ为圆点到点(x,y)的距离;θ为矢量ρ与x方向的夹角。
如图5a所示为Zernike矩理想边缘模型,图5b为图像绕坐标轴旋转θ角后的边缘阶跃模型,目标区域用阴影区域表示,h表示图像背景区域的灰度值,k是边缘阶跃高度,l是边缘线到原点的垂线长度,θ为边缘线到原点的垂线与x轴的夹角。
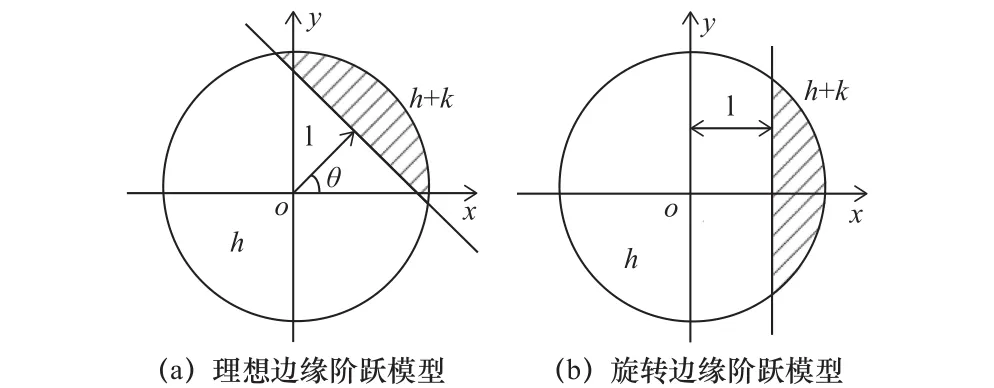
图5 Zernike矩理想边缘模型
设边缘阶跃模型绕坐标轴旋转θ角,根据Zernike矩旋转不变性可得

由式(5)中可知旋转后的图像关于x轴对称,并且只有相角发生了变化。将旋转后的理想边缘阶跃模型积分可得


基于Zernike矩的模板效应,需要对亚像素坐标进行修正,利用式(7)对各项参数进行运算,求得修正后的亚像素边缘坐标为

式中:A为模板阶数,本文采用7×7模板阶数。(xs,ys)为修正后图像的亚像素边缘坐标。
3.2 基于运算时间的改进
传统的Zernike亚像素边缘检测算法需要遍历计算所有像素点的多个正交复数矩,计算效率低且计算时间长。为了减少运算时间,提高亚像素边缘检测的效率,本文引入Canny边缘检测算法,通过Canny算子对预处理过的图像进行检测来实现粗定位,从而将 Canny边缘检测与Zernike 矩亚像素边缘检测相结合。收集并保存所有Canny算子定位的边缘点,然后利用Zernike 矩算法对可能的边缘像素点进行正交复数矩计算,从而实现亚像素点的精确定位。
3.3 改进的Zernike矩边缘检测算法实现
本文通过Canny算子对齿轮图像进行边缘检测,并保存所有可能的粗定位边缘像素点。使用7×7模板,将模板系数与粗定位边缘像素点做卷积运算,并通过式(7)求取边缘参数k 、h、 l和θ。当粗定位边缘像素点满足Zernike矩边缘点判断条件k≥kt且l≤lt时,判断该像素点为边缘点,并通过式(8)进行精确计算,获取亚像素级坐标。遍历粗定位边缘像素点即可得到亚像素边缘。
4 齿轮参数的测量
4.1 齿轮基本参数的测量
(1)齿轮中心(x0,y0)
参照组使用传统开胸手术方法,患者进行全身麻醉,在患者第5肋间进行消毒后[3],做手术切口,在确定病灶位置后,将病灶切除,并清扫淋巴结,然后缝合患者伤口并消毒。实验组使用微创手术方法,患者行静脉复合全身麻醉,气管插管,在患者的第4肋间做主操作孔,第8肋间建立辅助操作孔,第7肋间建立观察孔,将患者病灶切除后,要清洗胸腔[4-7],然后缝合伤口。
齿轮中心作为齿轮参数测量最基础也是最重要的参数,其定位的准确度将直接影响后续齿轮参数测量的精度。经过多种方法比较,本文使用重心法进行求取。首先对齿轮的亚像素边缘进行填充,再对填充的齿轮图像进行连通区域标识,通过计算得到连通区域的重心点坐标,此坐标即为齿轮中心。
(2)齿顶圆半径ra
本文采用凸包法求解齿顶圆半径,通过凸包算法在齿轮亚像素边缘轮廓外构建外凸包结构,将外轮廓的像素点全部包含在外凸包结构内。外轮廓与外凸包结构会产生多个交点,此时可将交点视为齿轮齿顶圆上的像素点,计算交点到齿轮中心的距离并取平均值,即为齿顶圆半径。凸包结构图如图6所示。

图6 凸包结构图
(3)齿根圆半径rf
求解齿根圆半径需要先求解出齿轮外轮廓到齿轮中心的距离,此时,齿轮外轮廓到齿轮中心的距离最小的点及其周围轮廓点可视为齿根圆上的点,将得到的距离最小的40个点视作齿根圆上的点,计算这些点到齿轮中心的距离并取平均值,即为齿根圆半径。
(4)齿数z
本文使用统计连通域法实现齿轮齿数的快速测量,在获得齿顶圆和齿根圆的半径后,以齿轮中心为原点,以二者的平均值为半径画圆,以此设计掩模模板,在掩膜中将圆内部灰度值设为255;通过将掩膜与填充后的齿轮图像相乘,获取代表齿牙的连通区域;最后统计连通区域的个数,即可得到齿轮的齿数。掩膜结果如图7所示。

图7 掩膜处理后的连通域
(5)模数m、分度圆半径r
本文通过已测得的齿轮参数来求取齿轮模数和分度圆半径。齿轮模数m计算公式如式(9)所示,式中齿顶高系数取1。分度圆半径r计算公式如下。

4.2 齿距偏差的测量
求解齿距偏差需要求解齿轮的基本参数,求解齿轮齿距偏差的流程图如图8所示。
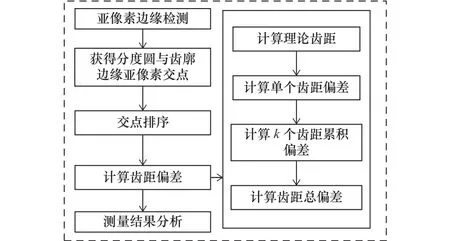
图8 齿距偏差测量流程图
本文利用机器视觉测量齿轮的齿距偏差,通过将分度圆与齿轮轮廓相交得到的交点作为依据进行分析,可以实现齿距偏差的精确计算。齿距偏差主要3个衡量方法,分别为单个齿距偏差Δfpt,k个齿距累积偏差Δfpk和距累积总偏差ΔFpk。其算法设计如下:
(1)设定两幅大小为m×n,背景灰度值为255图片picture1、picture2。在图片picture1中,搜索齿轮轮廓的点,并把轮廓点灰度值设为50;在picture2中,以齿轮中心为圆心画分度圆,并把分度圆点的灰度值设为100,picture1和picture2相加,遍历灰度值为150的点,这些点就是分度圆和齿轮亚像素边缘的交点,并将这些点按顺时针顺序标记为p1,p2,… ,p2k(z为齿轮齿数)。交点顺序如图9所示。

图9 交点顺序
(2)以p1为起始点,求出与其相邻的同侧齿廓的交点p3和圆心之间的角度∠p1op3。
设两交点的坐标为(x1,y1),(x3,y3),由平面旋转矩阵原理可得

两交点之间距离和夹角为

由此可得任意两交点ma、mb间的夹角为

(3)计算两交点理论齿距p,可得

(4)求出对应的齿距偏差。
计算单个齿距偏差 Δfpi,得
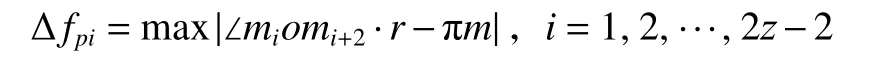
计算k个齿距累积偏差Δfpk,得

计算齿距累积总偏差ΔFpk,得

5 实验结果与分析
为了验证基于机器视觉的直齿轮齿距偏差测量方法的准确性,本文使用齿顶圆直径为120 mm,模数m=3 mm,齿数z=38的直齿圆柱标准齿轮作为实验对象。
5.1 齿轮基本参数测量
设计程序实现前述的算法,并分别使用本文算法和人工测量完成齿轮参数测量,并对测量结果进行比较和分析,人工测量如图10所示,测量结果如表1所示。

图10 人工测量
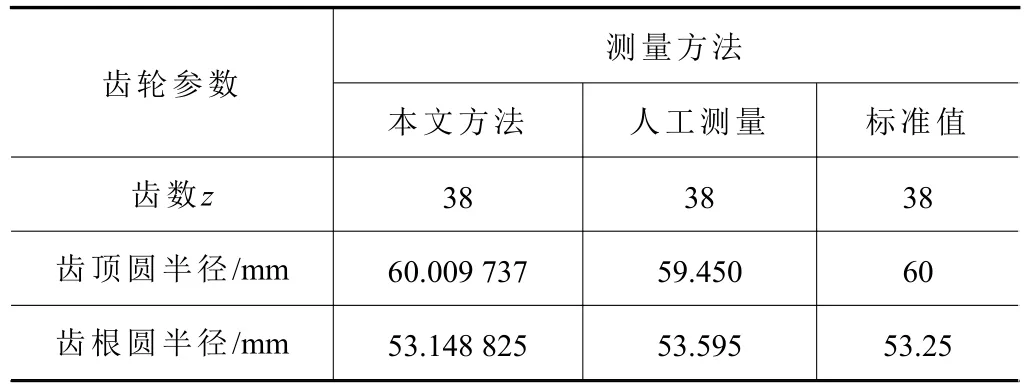
表1 实际尺寸与测量尺寸结果
对比本文算法和人工测量的齿顶圆、齿根圆半径值。本文算法精确度高于人工测量,且误差在0.02%以内,可以满足实际测量需求。
5.2 齿距偏差测量
由前述齿距偏差测量方法,对单个齿距偏差和任意k个齿距累积偏差进行了测量,由前述可得,本系统像素当量:K=0.018 mm/pixel=18 μm/pixel。由表2可知,最大单个齿距偏差为11.81 μm。

表2 任意单个齿距偏差测量结果 μm
如图11所示,折线分别代表左齿面和右齿面的k个齿距累积偏差的测量结果,由于k值取小于z/8的最大整数,本文取k=4。由图可知,左齿面最大k个齿距累积偏差23 μm,右齿面最大k个齿距偏差17 μm。齿距累积总偏差21.05 μm。各项偏差的最大值都在合理范围之内。

图11 k个齿距累积偏差
6 结语
本文采用于机器视觉检测方法对齿距偏差进行检测,并通过直齿轮(齿顶圆直径为120 mm,模数m=3 mm,齿数z=38)进行了实验验证。实验表明,齿顶圆和齿根圆直径的最大误差小于0.02%,左齿面最大单个齿距偏差为11.81 μm,右齿面最大单个齿距偏差为10.6 μm。k个齿距累积偏差和齿距累积总偏差均满足6级精度等级。在后续的研究当中,还需要进一步研究齿轮的其他几何特征精密测量方法,提高综合应用性。

