基于多尺度特征融合的改进臂丛神经分割方法
吕玉超,姜 茜,徐英豪,朱习军
(青岛科技大学 信息科学技术学院,山东 青岛 266061)
0 引言
在术前麻醉环节,臂丛神经是首选的麻醉位置,能否得到更为完整具体的臂丛神经分割是提高局部麻醉性能的关键。超声影像凭借其良好的穿透性,能够直观地确定测试对象的病变形态及特征;再加之成熟的技术以及较低的试验成本,已经成为臂丛神经区域的主要成像手段。有研究表明,与盲探臂丛神经阻滞相比,超声定位引导下的臂丛神经阻滞的不良反应发生率降低了85.73%[1],神经阻滞的总有效率提升了13.10%[2]。因此,在临床术前检查时,国内外医院大多利用超声技术对臂丛神经进行检查,并在此基础上进行麻醉引导[3]。
然而,超声影像广泛存在对比度低、斑点噪声多的特点;而臂丛神经的结构较小,更容易受到噪声影响,细节特征信息更容易被掩盖,受此影响,传统分割方法的分割效果并不理想。目前的分割任务还主要由医师人工完成,但人工分割工作较为困难,判断结果的优劣程度受医师水平及经验的影响较大。因此,如何进行高效、准确的臂丛神经分割成为相关工作的重点。
针对臂丛神经超声影像分割任务中图像信噪比(Signalto-Noise Ratio,SNR)低、边缘模糊、目标区域小、形状不规则的问题,本文设计了一种针对神经部位分割的特征金字塔网络(Nerve-segmentation Feature Pyramid Network,Ner-FPN)。在特征提取阶段设计一种仿Xception[4]结构,通过使用不同尺度感受野进行特征提取,堆叠形成5 维特征金字塔;同时,为充分利用已获得的多维特征,更好地融合特征表现,在分割预测阶段设计一种基于双向FPN[5]的网络结构,对所得特征金字塔进行双向多尺度融合预测;此外,为防止训练过程中出现过拟合现象,减少模型的参数量,还使用了残差结构[6]以及深度可分离卷积[7],以达到更好的训练效果。实验结果表明,Ner-FPN 的准确率能够稳定保持在70%以上,具有较好的鲁棒性。
1 相关工作
医学图像的分割处理方法主要有两大类:一是基于传统思想的分割方法,包括基于图像色彩等特征的区域分割方法[8]、基于区域边界的阈值分割方法[9]、基于边缘像素的边缘分割方法[10]等。这类方法会按照不同特征维度所具有的相似特征,将图像划分为内部特征更为相似的区域,也因此不适于处理对比度小、信噪比低的超声影像。二是基于深度学习的分割方法,其中主流是基于编解码设计的SegNet(Segmentation Network)[11]以及U-Net[12]。前者具有更深的网络层数,通常具有较好的分割效果;但对图像细节信息分割不明显,难以提取到像素的位置信息及相关特征。后者利用跳跃连接对图像细节信息进行了补充,但对不同层次特征利用不充分,在小目标的分割任务中表现不尽人意。
另一方面,多尺度特征由于其在小目标检测任务中表现优秀,成为相关研究中的重点。以SSD(Single Shot multibox Detector)网 络[13]、TDM(Top-Down Modulation)网络[14]以及FPN[5]为主的三种不同模型方法各有千秋,尤以FPN 类网络结构对小目标区域的处理效果最好。近年来,在图像分割任务中,多尺度特征的应用逐渐受到青睐。赵小虎等[15]对SSD 网络模型进行改进,在Microsoft COCO Caption 等公开数据集上的一致性可达99.70%;但其网络结构过深,不适用于处理臂丛神经这一类语义单一的二维超声影像。高世伟等[16]提出了一种基于FPN 的实时语义分割算法,以每秒91 帧的速度取得了71.86%的准确率;但其模型没有针对各类分割目标的特点进行分类处理,没有从特征提取的角度进行改良。
臂丛神经分割的相关研究中,多尺度特征融合应用的研究相对匮乏,大多研究的重点仍然是对基本分割网络进行改进。龙法宁等[17]为防止过拟合,对U-Net 添加了Dropout 层,并结合臂丛神经裁剪区域单一且连续的数据特点,引入自定义损失函数,取缔了原像素级分割的策略,最终在BP(Brachial Plexus)数据集上的Dice 相似系数(Dice Similar Coefficient,DSC)可达65%。孔令军等[18]使用EfficientNetB3取代U-Net 模型中的编码层,通过在跳跃连接上使用空洞卷积达到去噪并提取位置信息的目的;实验结果表明,它在BP数据集上的DSC 为68.14%。但上述工作都没有解决U-Net本身对多维特征欠缺应用的根本问题。
此外,也有利用SegNet 进行臂丛神经超声影像的多实例分割任务的研究。Ding 等[19]应用跳跃连接和自注意力机制,提 出 BPMSegNet(Brachial Plexus Multi-instance Segmentation Network)进行臂丛神经的多实例分割,通过改变不同维度特征在分割过程中的权重,在私有数据集UBPD(Ultrasound Brachial Plexus Dataset)上准确率可达62.97%。针对超声影像斑点噪声多、边缘影响大的问题,杨桐等[20]结合ACE(Adaptive Contrast Enhancement)算法,对原始图像进行增强处理,并使用改进SegNet 进行分割,在采自北京积水潭医院超声影像以及对应的良性恶性肿瘤图片的数据集上能够以超过99%的准确率识别出图像中的四种不同组织。但上述多实例分割模型往往需要考虑实例之间的区分问题,对于高维和低维的特征应用相对固定,因此在单实例分割任务中的表现仍然不尽如人意。
综上所述,现有方法对臂丛神经分割的研究大多停留在解决臂丛神经超声图像中目标区域小、形状不规则的问题;同时,多尺度特征在目标检测任务中的广泛应用,也为利用多尺度特征进行臂丛神经分割提供了依据。
2 Ner-FPN
2.1 Ner-FPN模型设计
本文以仿Xception 结构为骨架,从FPN 模型的结构特点出发,设计了一种基于多尺度特征融合的臂丛神经分割模型,结构如图1 所示。
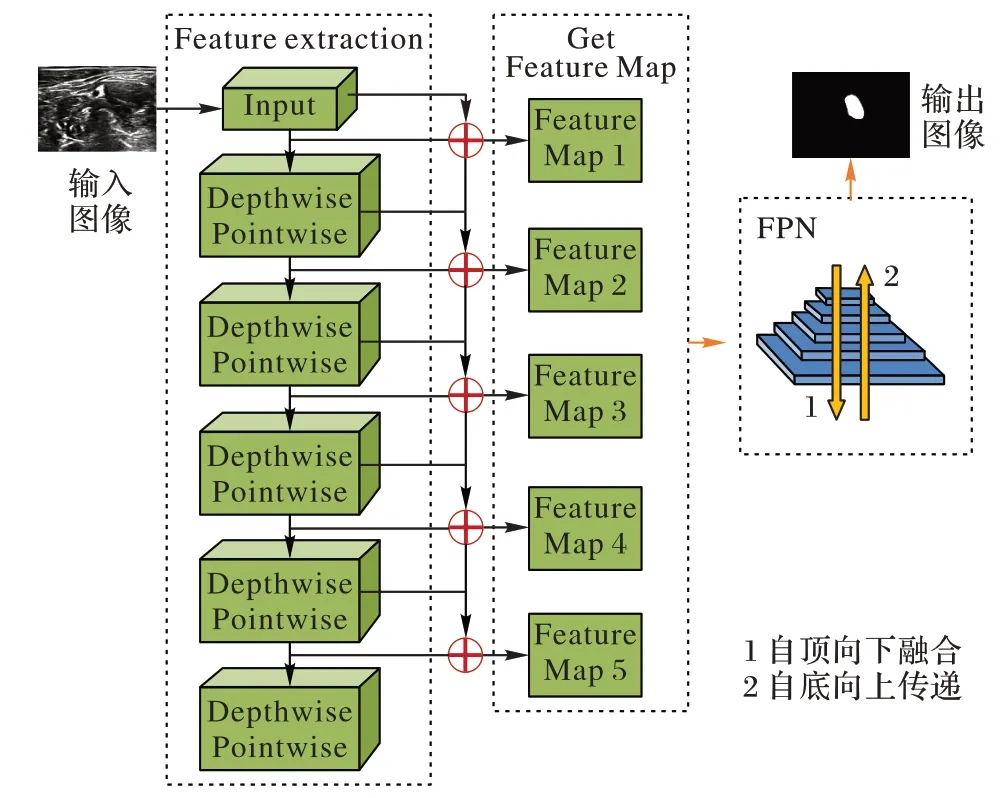
图1 Ner-FPN的模型结构Fig.1 Model structure of Ner-FPN
在图1 中,臂丛神经超声影像需要先通过特征提取(Feature Extraction)部分进行特征提取。在特征提取阶段添加残差模块以防止梯度消失,保留每一步所含有的全局信息。每一个深度可分离(Depthwise Pointwise)块为不同感受野大小的深度可分离卷积结构,每个模块需循环执行不同次数以获得该尺度下更深层次的特征,采用深度可分离卷积结构旨在增加网络深度的同时有效降低参数量,提高计算效率。在特征提取阶段通过每一步的残差结合,可以得到获取特征图(Get Feature Map)部分的5 张特征图(Feature Map)。将特征图堆叠为FPN 部分所示的特征金字塔,并采用双向的预测结构,先自顶向下进行融合,再自底向上传递预测结果,以此来获得最终的目标分割影像。
2.2 深度可分离卷积
为了解决大尺寸卷积所带来的计算量过大的问题,本文采用深度可分离卷积结构代替大尺寸卷积以达到同样的效果。该结构整合Depthwise 层和Pointwise 层,先对每个通道进行独立卷积,获取同一通道中的全局信息;再对每个像素点进行卷积,得到同一空间位置上的通道特征。这样的结构能够大幅降低参数量,提升运算速度。
由于本文模型在特征提取阶段需要用到不同尺寸的感受野,且对于不同特征层需要用到的卷积层数也不同。为了满足网络需求,缩短训练时间,本文采取了深度可分离卷积的结构来替代普通卷积。以获取128 通道数的两次卷积过程为例,如图2 所示。其中:W,B 分别表示网络层中的权重结构以及偏置量结构。
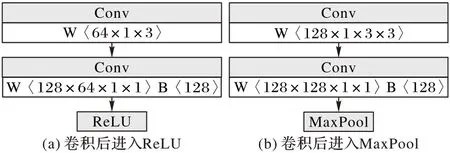
图2 深度可分离卷积处理过程Fig.2 Processing of depth separable convolution
在卷积过程中,先对每个通道进行独立的3×3 卷积,得到通道数为64 的卷积结果;再对上一步卷积结果中的每个像素点进行1×1 卷积,得到最终通道数为128 的卷积层。经过上述两步,则能够以较少的参数量完成一次常规的3×3 卷积。若所得结果为特征提取的中间结果则传入线性整流函数单元(Rectified Linear Unit,ReLU),如图2(a)所示;若所得结果为特征层的最终结果,则传入MaxPool 进行最大池化操作并等待进行残差连接,如图2(b)所示。按照上述计算方式,5×5、7×7 的卷积效果可以分别通过2 次、3 次的3×3 卷积实现。
2.3 多尺度特征提取模块
一方面,由于臂丛神经的目标区域小、受噪声影响大、信息隐藏深,导致相似图片内臂丛神经的位置、形状大相径庭,正负样本不平衡(如图2),因此适合采用多尺度特征提取的策略。高智勇等[21]在对肺结节的电子计算机断层扫描(Computed Tomography,CT)图像检测任务中也基于该思想设计了一种新的检测模型,并通过实验验证了其可行性。另一方面,受FPN 结构残差连接及多尺度融合特点的影响,在提取特征的过程中需要面对特征层次区分度过低、每层特征包含像素信息的重复度过大等问题。为避免上述问题,本文在特征提取阶段每一层特征图的提取过程中加入了不同深度的卷积,使最终得到的特征图之间有较好的区分度。
具体地,采用3×3、5×5、7×7 三种不同的感受野,对每个感受野设置不同的卷积次数,实现了一种对称式的特征提取结构,并以此获得了通道数为128、256、512、1 024 及2 048 的5 张不同层次的特征图,借此来尽可能丰富每张特征图所蕴含的本层的图像信息。在特征提取阶段,本文所采用网络结构的具体参数如表1 所示。

表1 多尺度特征提取模块参数Tab.1 Parameters of multi-scale feature extraction module
此外,由于在多次特征提取阶段容易出现梯度消失现象,本文在每层特征提取结束以后添加了残差模块。以通道数为128 的特征提取阶段为例,在进行特征提取的同时需要将输入特征图进行1×1 卷积,改变其图像大小,增加通道数,再利用残差结构连接。具体的残差连接结构如图3 所示。

图3 128维特征提取的残差连接结构Fig.3 Residual connection structure of 128-dimensional feature extraction
在上述多特征特征提取模块中,每一层的处理都在上一层的结果上进行,以此来获得较低层特征更高级的图像信息;每个层次的最终输出都将作为特征金字塔的一层参与分割预测。通过这样的方式,最大化利用每一层的特征信息,进一步实现分割时对隐藏信息的提取。
2.4 双向FPN预测结构
在近年的研究中,FPN 在图像分割领域已取得非常优异的表现[22-24]。FPN 通过将获得的不同尺度的特征进行自顶向下的预测与融合,能够较好地照顾到不同层次的特征信息,契合以小目标区域分割为核心的臂丛神经分割任务。因此,本文采用FPN 结构进行分割。一方面,由于在多尺度特征提取模块已经获得了层次较高的图像信息,为了照顾到模型的整体参数量,本文不考虑采取循环特征金字塔结构;另一方面,臂丛神经的边缘信息隐藏较深,受低层或高层特征影响不均衡,训练用正负样本极不平衡,因此,本文不考虑应用注意力机制。
基于上述分析,本文采取一种双向FPN 结构[25]来进行分割工作。对于在特征提取阶段中得到的5 层特征金字塔,首先对每层特征进行卷积,使之转为256 通道数的特征层;其次,自顶向下地对相邻两层进行残差连接;再对结果分别进行5、4、3、2 和1 次的反卷积,转换为5 个128 通道数的特征层,并在其中进行图像大小变换(Reshape)、实例归一化(Instance Normalization,IN)等操作,使之变为128×256×256的特征图,每步的具体处理方式如图4 所示。

图4 特征金字塔中单层特征的处理过程Fig.4 Processing of single-level features in feature pyramid
经过如图4 的处理阶段之后,此时的5 层特征已具备相邻高层特征的空间信息,并通过降维操作减少了参数量,这样的5 张特征图即是每一层的预测结果。最后,将5 层特征图自底向上融合,通过Sigmoid 函数得到分割结果。
3 实验与结果分析
本文配置的实验环境如下:CPU 为Intel Xeon Gold 6142 CPU@2.60 GHz,8 核,GPU 为NVIDIA GeForce RTX 3080,显存10 GB,磁盘435 GB,内存29 GB,Linux 操作系统,PyTorch 1.10 深度学习框架。
3.1 数据来源及处理
数据来自于Kaggle 平台上2016 年的Nerve Segmentation Competition 用公开数据集,即BP 数据集(https://www.kaggle.com/competitions/ultrasound-nerve-segmentation/overview/description)。该数据集图像大小为580 像素×420 像素,均为tif 格式文件。数据集包含两个数据子集,分别为包含了5 635 张图像样本的训练子集和包含5 509 张图像样本的测试子集,所有数据均由真实臂丛神经超声影响获得。另外对训练子集进行了人工标注,生成了5 509 张图像掩膜。部分图像样本及其掩膜如图5 所示。由图5 能够看出,在超声影像中臂丛神经的形状并不规则;此外,当前5 635 张训练样本对于深度学习训练而言样本量较小,因此本文进行了数据增强处理。如图6 所示,主要采用对数据随机进行旋转(图6(b))、镜像(图6(c))和添加高斯噪声(图6(d))等方式对数据进行预处理,以8.5∶1.5 的比例随机划分训练集与验证集。通过上述方式来实现数据增广,增大数据样本量,提高模型的泛化能力。

图5 臂丛神经超声影像数据示例Fig.5 Examples of brachial plexus nerve ultrasound imaging data

图6 超声影像数据增强处理Fig.6 Enhancement processing of ultrasound image data
3.2 训练参数及评价指标
本文输入图片的大小为256×256,使用Adam 优化器,初始学习率设置为0.001 3,采用ReduceLROnPlateau 策略,以0.2 为步长调整学习率,采用Dice_Loss 为损失函数,训练50轮次。
在图像分割领域,当前常用的评价标准有Dice 相似系数(Dice Similarity Coefficient,DSC)和平均交并比(Mean Intersection over Union,MIoU)。DSC 用于计算两个样本的相似度,计算公式如式(1)所示:

其中:TP(True Positive)表示被正确分割为臂丛神经的像素数目;FP(False Positive)表示被错误分割为臂丛神经部分的背景像素数目;FN(False Negative)表示被错误标记为背景的臂丛神经像素数目。
交并比(Intersection over Union,IoU)是计算真实值与预测值两个集合的交集与并集之比,其计算公式如式(2)所示。MIoU 是计算其平均值,计算公式如式(3)所示:
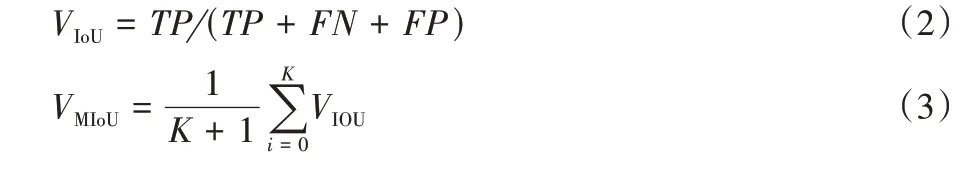
其中:K为样本数目。
除此之外,还有诸如区域重叠率(Area Overlap Measure,AOM)、区域过分割率(Area Over-segmentation Measure,AVM)、区域欠分割率(Area Under-segmentation Measure,AUM)等指标,由于本文采用的BP 数据集在Kaggle 平台的评价标准为DSC,因此不考虑其他评价标准。Ner-FPN 模型的网络训练过程如图7 所示,由图7(a)可以看出模型在35 轮次后开始达到收敛并趋于稳定;由图7(b)可以看出在35 轮次后,模型的DSC 及MIoU 均取得了良好且稳定的结果。

图7 Ner-FPN模型的训练过程曲线Fig.7 Curves of Ner-FPN model training processing
3.3 分割性能对比
为验证Ner-FPN 模型的有效性,本文设计了Ner-FPN 模型与当前主流研究的U-Net 类网络的对比实验。采用原始U-Net[12]、SegNet[11]、QU-Net[17]和Efficient+U-Net[18]进行对照,实验采用相同的环境、训练参数以及损失函数。其中测试集采用Kaggle 官方测试集,返回结果仅DSC。实验结果如表2所示。

表2 不同模型的预测结果对比Tab.2 Comparison of prediction results among different models
通过表2 可以看出,Ner-FPN 模型在测试集上表现良好,在验证集上的DSC 及MIoU 明显优于U-Net、SegNet,对比两个改进U-Net 模型(QU-Net 和Efficient+U-Net)也具有更好的鲁棒性。其中,由于Efficient+U-Net 结构具有更好的深度、广度及特征图分辨率,在训练集及验证集上的表现优于Ner-FPN 模型;但与QU-Net 相似,Efficient+U-Net 不可避免地容易过拟合,因此在测试集上的表现欠佳。另外,Ner-FPN 模型在测试集上的DSC 为0.703,与U-Net、SegNet 模型对比,分别提 高了10.7,14.5 个百分 点;与QU-Net、Efficient+U-Net 对比,也分别提高5.5 和3.4 个百分点,显著优于其他对比模型。这足以说明如前文所述的仿Xception 多尺度特征提取模块以及双向FPN 的预测模块起到了实质性作用。为更直观地表现其结果差异,预测结果示例如图8 所示。
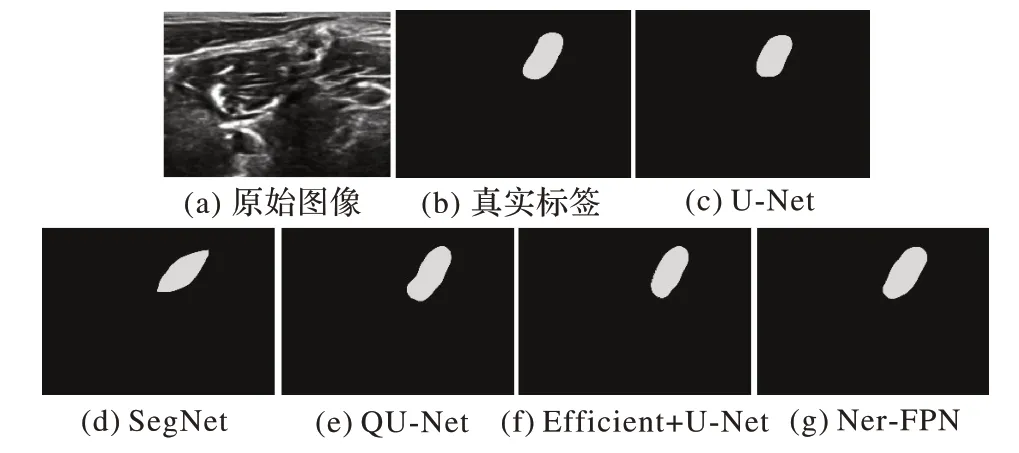
图8 不同模型预测结果示例对比Fig.8 Comparison of prediction results examples among different models
3.4 消融实验
在影响模型的分割准确率上,针对多尺度特征提取模块、双向FPN 预测模块以及特征提取中的残差模块三部分进行消融实验;在影响模型的体量(模型参数量、模型大小和模型的计算量)上,针对深度可分离卷积模块设计消融实验。
针对多尺度特征提取模块的实际效果,本文以普通的双向FPN 模型、U-Net 结构的双向FPN 模型以及残差网络(Residual Network,ResNet)结构的双向FPN 模型为对照进行实验;针对双向FPN 结构在预测阶段的所取得的效果,本文又采用以多尺度特征提取结构为特征提取模块的U-Net、SegNet 以及原始的单向FPN 模型作为对照;针对特征提取中残差结构的有效性,本文分别以每个特征提取子模块在循环执行中的首次结果、中间结果及最终结果作为特征图的FPN构建方式,进行对照实验。其中:首次结果取每个特征提取模块在循环执行中的第一次特征图;中间结果取循环执行过程中各特征图的算术平均;最终结果取循环执行中的最后一次特征图。
以上实验采用相同的实验环境、训练参数以及损失函数,针对影响模型准确率的三个模块消融实验结果如表3所示。
由表3 可知,首先,同样具备双向FPN 预测模型的三种网络,多尺度特征提取模块能够有效提取并利用不同层次的特征。即使是U-Net 这一对多尺度特征稍加利用的结构,对比普通的双向FPN 也能够较好地提升准确率;但碍于其对低层特征的应用有限,提升较少。

表3 影响模型准确率的模块的消融实验结果对比Tab.3 Comparison of ablation experimental results of modules affecting model accuracy
其次,对比同样搭配多尺度特征的三类模型,双向FPN结构在预测上的效果提升也较为明显,尽管各个模型在验证集上表现相仿,但对不同层次特征内容利用越充分的预测结构在测试集上的表现越好。
最后,在利用不同层次特征图的Ner-FPN 模型中,选取同尺度下越深层的特征图构建FPN,整体分割效果越好;但选取最终结果的提升较中间结果提升不明显,考虑其特征图层次过深,低层信息利用不完全,相比之下,通过残差连接的Ner-FPN 对各信息层的利用更为充分,提升明显。综上所述,上述三种结构对于Ner-FPN 模型的建立都具有积极影响。
另一方面,为验证深度可分离结构对参数量以及模型计算量的影响,与原始感受野大小的模型结构进行了对照实验。在相同的实验环境、训练参数以及损失函数下,针对深度可分离卷积模块的消融实验结果如表4 所示。通过表4 可以明显看出,深度可分离卷积的结构能够有效减少模型参数量,同时该结构也在一定程度上加深了网络层次。

表4 影响模型参数量及计算量的模块的消融实验结果对比Tab.4 Comparison of ablation experimental results of modules affecting parameters and computing cost
4 结语
本文针对臂丛神经超声影像的语义分割任务进行了深入分析,提出了一种基于多尺度特征融合的改进臂丛神经分割方法。该模型能够有效地适应超声影像信噪比小、边缘模糊的特点,针对超声影响中,臂丛神经目标区域小、目标不规则的特点,得到较好的分割结果。实验结果表明,该模型的分割准确率明显优于其他对比模型,所设计的仿Xception 结构多尺度特征提取模块及双向FPN 模块能够有效应对臂丛神经分割任务,对同类问题可提供一定参考。由于本文模型仅在一种数据集上进行测试,因此缺乏一定的泛用性;在后续研究中,会进一步考虑引入更加丰富的数据,并在其他任务上尝试进行迁移,提升模型的实际应用价值。

