分布式环境下大规模移动对象范围查询算法

马永强，陈晓萌，于自强*

（1.自然资源部城市国土资源监测与仿真重点实验室，广东 深圳 518034；2.烟台大学 计算机与控制工程学院，山东 烟台 264005）

0 引言

移动对象查询问题近年来被广泛研究［1］。本文研究的移动对象连续范围查询是指给定一个移动对象集合O、一个查询点qi及其查询范围sqi，查询范围内的移动对象，并随着移动对象和查询点的不断移动，对qi的查询结果进行连续更新。大规模移动对象的连续范围查询是许多基于位置服务的核心问题。例如，打车软件为查找附近的出租车，此时用户和出租车可以分别被视为查询点和移动对象。现实中，打车软件通常需要为移动的用户持续更新周围的出租车，其本质是以用户为查询点的移动对象连续范围查询。

近年来，尽管移动对象范围查询已经被大量研究，但仍存在以下问题亟待解决。

在索引结构方面，已有工作通常设计基于R-tree 索引结构或网格索引结构的移动对象范围查询算法。R-tree 索引［2-3］结构虽然能够有效支持移动对象范围查询，但是由于树型结构整体性较强，且维护代价较高，难以直接部署到服务器集群的分布式计算环境中。网格索引结构［4-8］虽然易于部署到基于服务器集群的分布式计算环境中，但是面对范围查询时，剪枝能力有待加强，主要体现在处理与范围查询部分重叠的单元格时，仍然需要对该单元格内所有移动对象进行判断以确定它们是否被查询范围覆盖。当并发查询数量大、单元格内移动对象较多时，处理大量类似单元格将消耗大量的计算资源。例如，图1（a），查询qi的查询范围与8 个单元格部分相交，此时就需要对8 个单元格内所有移动对象进行遍历，查询效率有待提高。

在计算模式方面，已有绝大多数范围查询相关工作［9-12］都是针对单个计算节点设计的集中式查询算法，然而，现实中基于位置服务通常需要在短时间内处理大量并发的移动对象范围查询。此时，集中式查询算法受限于单个计算节点的计算资源，难以高效处理大规模并发的移动对象范围查询，而本文设计基于服务器集群的分布式查询算法（Distributed Search Algorithm，DSA）是解决这一问题的有效方案。

针对上述问题，本文研究分布式环境下移动对象范围查询算法。目前，已有相关工作对分布式环境下的移动对象范围问题进行研究［13-15］，这些工作是将移动对象看作移动重点，通常是将每个移动对象看作一个移动计算终端，这些移动终端和数据中心构成一个偏向边缘计算的分布式计算环境，这与本文基于服务器集群的分布式计算环境截然不同。首先，这种偏向边缘计算的分布式模式是将大量的计算分配到移动终端，移动终端与数据中心较大的通信代价是衡量系统性能的主要指标；本文的分布式计算模式是将同一查询的计算任务均衡地分配给多个服务器并行处理，服务器之间的通信代价较小，计算代价是主要考虑的性能因素。其次，偏向边缘计算的分布式计算模式要求移动终端具有较强的计算算力，一定限度上限制了该算法在现实中一些低计算性能终端（如车载GPS）上的应用；本文的分布式计算模式仅要求移动对象能够发送当前位置即可，绝大多数移动对象均具备这一功能。

针对上述问题，本文首先提出一种由网格索引和动态四叉树索引构成的移动对象分布式动态索引（Distributed Dynamic Index，DDI）结构。该索引结构首先将整个查询区域划分为n×n个大小相等的单元格，每个单元格记录它所包含的移动对象；每个单元格相互独立，可以部署到多个不同物理计算节点上。为增强网格索引的剪枝能力，当一个单元格内的移动对象数量超过阈值α，则为该单元格构建一棵动态四叉树。动态四叉树的构建原则是将整个单元格看作根节点，当一个节点内的移动对象数量大于α时，则为该节点增加4 个孩子节点，单元格内的移动对象保存在四叉树的叶子节点中；若具有同一父节点的4 个叶子节点的移动对象数量之和小于α，则删除该4 个叶子节点，其父节点变为孩子节点。随着移动对象的位置变化，每个单元格的四叉树深度动态调整，从而获得合适的索引粒度。本文提出的DDI 结构能够有效增强针对范围查询的剪枝效力。图1（b）中，查询qi的查询范围覆盖单元格c7，可直接将c7内所有移动对象作为qi的部分查询结果；对于查询qi所涉及的其他单元格（除c7以外），则遍历每个单元格对应的四叉树索引结构。此时，查找这些单元格中被查询qi覆盖的移动对象时，不必再遍历这些单元格中所有移动对象，而是对每个单元格对应四叉树中不同层级的节点进行搜索，即可快速得到被查询范围覆盖的移动对象，显著提高查询效率。

图1 DDI结构Fig.1 DDI structure

由于DDI 结构中各个单元格之间相互独立，因此整个索引结构易于部署到采用Master-Worker 架构的分布式计算环境中。基于DDI 结构，本文进一步提出了一种针对范围查询的分布式查询算法（DSA）。该算法将每个范围查询分解为多个单元格上的子查询，这些子查询可以由多个计算节点并行计算，从而提高查询效率。对范围查询进行连续搜索时，DSA 尽可能利用该查询上一时刻已有结果增量计算当前时刻最新结果。此外，每个计算节点采取一种共享计算机制，对其处理的涉及相同查询区域的多个并发范围查询共享计算结果，进一步降低计算代价。

本文的主要工作如下：

1）提出一种基于网格索引和弹性四叉树的移动对象分布式动态索引结构DDI，它易于部署到分布式计算环境下，并且能够根据移动对象的分布密度动态调整每个单元格的索引粒度，具有更强的剪枝能力。

2）提出一种面向大规模移动对象并发范围查询的分布式搜索算法DSA，并设计了面向连续范围查询的增量搜索和共享计算策略，该算法具有良好的可扩展性。

3）将所提算法部署到流数据分布式计算平台Storm 上，并在实验中与NS（Naive Search）、GI（Grid Index）和分布式混合索引（DHI）进行对比，评估本文所提出方法的性能。

1 相关工作

移动对象的范围查询作为基于位置服务领域的基本问题被广泛研究，本文根据已有工作所采用的移动对象索引结构、查询场景和计算模式对其进行梳理和介绍如下。

移动对象网格索引被广泛应用于移动对象查询［4-9］。Kalashnikov 等［4］指出基于网格索引的查询性能相较于其他索引结构更加优越，并提出一种基于排序的优化方法以提高缓存命中率；Dong 等［5］和董天阳等［6］建立移动对象网格索引，可根据方向感知道路网络以确定向查询点移动的移动对象；薛忠斌等［7］提出一种基于内存的高吞吐量移动对象范围查询算法，可一次执行多个查询，实现了查询间的并行；Yu等［8］提出了一种基于网格对移动对象高效索引的可伸缩算法，可以提高查询性能和对移动对象密集分布的鲁棒性。

此外，文献［10-12］中引入了“安全区”的概念来解决移动对象查询问题。“安全区”是根据查询范围边界内部/外部的最近移动对象到查询边界的距离计算的查询移动区域，在该区域中，查询点的移动不会导致查询结果发生变化。Al-Khalidi等［11-12］研究了一种静态近似距离搜索算法，该算法可以快速确定“安全区”上/下界限近似范围，使指定安全区内的查询避免重复计算。

随着室内位置服务的日益普及，室内移动对象的距离感知查询研究在过去的几年里受到了一些学者［16-18］的重视。Wang 等［17］根据不同距离的边界拥有不同查询评估，对不确定室内距离的移动对象关系进行了定义和分类。Shao 等［18］指出，室内空间的特性未被现有的索引和查询技术充分利用，因此，他们在充分考虑室内场地特性的基础上提出了室内分区树（Indoor Partitioning Tree，IP-Tree）和生动的室内分区树（Vivid IP-Tree，VIP-Tree）两种新的索引结构。

上述大多数算法是集中式算法，受限于单个节点的计算能力，难以应对大规模的并发查询。为此，Silvestri 等［19］采用一种基于CPU 和GPU 混合使用的并行算法处理大规模移动对象范围查询。此外，一些工作研究了面向移动对象范围查询的分布式搜索算法。其中文献［13-15］采用边缘计算的思想进行范围查询，这类算法通常要求移动终端具有较强的计算能力，使得该类方法的适用性受限；与之不同的是，文献［3，20-21］中采用基于服务器集群的分布式计算思想。其中：冯钧等［20］提出一种静态范围查询算法，对查询点相邻的路段进行递归，以更新查询范围内路段上的移动对象；但在处理大规模并发查询时，创建多个索引表会给系统带来巨大的额外负载。针对上述问题，徐江峰等［21］则提出了一个多维索引框架New-grid，该框架采用基于Hilbert 曲线的线性化技术解决此问题，同时指出网格索引在分布式环境下具有良好的可扩展性；但在处理与范围查询有交集的候选单元格时，这些算法仍需遍历候选单元格内所有移动对象。Yu等［3］提出了基于网格索引和R-tree 的混合分布式索引结构用于解决该问题。但当移动对象位置发生变化时，该索引结构的每个单元格对应的R-tree 自底向上不断更新，需要进行频繁维护，导致整个索引的维护代价较大；此外，该算法未考虑多个并发范围查询之间的共享计算问题，本文认为对涉及相同区域的多个并发范围查询，共享计算能够有效提高查询效率。

2 相关定义

表1 是本文拟采用的符号与含义说明。

表1 符号及其含义Tab.1 Symbols and their meanings

定义1移动对象。移动对象被表示为一个三元组oi={IDi，tc，(xi，yi)}，即oi的唯一标识IDi在tc时刻的位置为(xi，yi)。

定义2连续范围查询。连续范围查询是指给定查询点qi及查询范围sqi，从查询qi初始时刻计算位于sqi范围内的移动对象集合然后随着查询点和移动对象位置的变化，不断地更新移动对象集合Oquery，直到查询终止时间。

本文中，查询qi的查询范围sqi可以是任意多项式表示的形状。为便于表述，本文假设sqi为圆形。

定义3单元格。本文将整个搜索区域划分为若干相同大小的单元格。每个单元格ci采用OLi、FLi和PLi这3 个列表分别记录它所包含的移动对象、查询范围完全覆盖ci的查询点以及查询范围部分覆盖ci的查询点。

定义4候选单元格。对于范围查询qi，如果单元格ck完全或部分被sqi覆盖，那么ck是查询qi的候选单元格。ck⊆sqi表 示ck被sqi完全覆 盖，ck⊂sqi表 示ck被sqi部 分覆盖。

3 移动对象分布式索引结构

3.1 分布式索引结构模型

本文提出的移动对象分布式动态索引（DDI）结构由网格索引以及动态四叉树两部分构成。

3.1.1 网格索引结构

网格索引将整个查询区域划分为大小相同的单元格。每个单元格ci维护OLi、FLi和PLi这3个列表，分别记录它所包含的移动对象、查询范围完全覆盖ci的查询点以及查询范围部分覆盖ci的查询点。当单元格ci记录的移动对象数量达到阈值α时，单元格ci则会构建一棵动态四叉树Ti作进一步索引。

3.1.2 动态四叉树索引结构

首先，四叉树的每个叶子节点nf维护一个移动对象列表NLf，记录被该叶子节点覆盖移动对象的唯一标识（ID）。四叉树的每个非叶子节点ni维护一个查询列表QLi，记录查询范围sqi能够完全覆盖该节点的查询ID。每个叶子节点nf也维护一个查询列表QLi，记录查询范围完全覆盖该叶子节点或者与该叶子节点部分相交的查询ID。随着移动对象的变化，Ti可根据移动对象的分布密度动态调整树的深度。具体而言，如果Ti中某个叶子节点中移动对象数量大于等于指定的移动对象数量阈值α，则该叶子节点进行递归分裂，直至每个叶子节点内移动对象数量小于阈值α；如果Ti中具有同一父节点的一组叶子节点中移动对象数量之和小于阈值α，则该组叶子节点将被删除，所包含的移动对象将由其父节点保存。

图2 给出了单元格ci对应的四叉树索引结构。图2（a）给出单元格ci对应四叉树的构建过程。其中，设定α=4，由于单元格ci中移动对象数量多于α，则将单格ci看作根节点，为其添加4 个孩子节点（n1、n2、n3、n4）。由于n1、n2中的移动对象数量大于α，则进一步为其分别增加孩子节点，直至所有叶子节点的移动对象数量小于α，对应的四叉树索引结构如图2（b）所示。对于查询q1，其查询范围sq1完全覆盖n1、n11，故将q1插入到n1、n11的查询列表；由于sq1与叶子节点n3、n4、n9、n10、n12部分相交，故将其插入到n3、n4、n9、n10、n12的查询列表。

图2 动态四叉树索引Fig.2 Dynamic quadtree index

网格索引中引入动态四叉树索引结构的目的是处理与某单元格部分相交的范围查询时，避免对该单元格中所有移动对象进行遍历。具体而言，如果单元格ci包含大规模移动对象且与查询范围sqi部分相交，那么查找属于ci且被sqi覆盖的移动对象需要遍历ci中所有移动对象，耗时较大。每个单元格中引入动态四叉树后，可以对该单元格内的移动对象进行不同粒度索引，查询算法只需遍历四叉树的部分节点就能得到准确查询结果，有效降低计算代价。

由于DDI 结构每个单元格作为一个独立的索引单元，可以部署到分布式集群的任意物理计算节点。每个计算节点可以根据自身负载维护任意数量的网格索引，从而使得DDI结构具有良好的可扩展性。

3.2 DDI结构的构建

构建DDI 结构是指将移动对象和连续范围查询插入到不同的单元格及其对应的四叉树中。

3.2.1 移动对象的插入

算法1 给出将移动对象oi插入算法的伪代码。首先识别当前oi所在的单元格cj，随后将oi添加到单元格cj的移动对象列表OLj，最后将且oi插入到cj对应的四叉树Ti中。在插入四叉树过程中，先从Ti的根节点逐层向下扫描，确定覆盖oi(xi，yi)的叶子节点nf，再将oi添加至nf的移动对象列表NLf（4）～8）行）。如果该叶子节点nf中移动对象数量达到阈值α，则进行分裂行成新的叶子节点，其中所有移动对象分别插入到对应的新叶子节点中（9）～10）行）。

算法1 中，给定移动对象oi(xi，yi)，分别根据横坐标xi和纵坐标yi确定oi所在单元格所需时间为T(2n)。设所插入单元格对应四叉树的节点数量为m，确定oi所在四叉树叶子节点所需时间为T(log4m)，因此，算法1 的时间复杂度为O(n+log4m)。

算法1 添加移动对象至四叉树。

3.2.2 插入连续范围查询

算法2 给出将连续范围查询qi插入到DDI 的伪代码。首先确定与范围查询qi相关的单元格：对于被查询范围sqi完全覆盖的单元格cj，qi被直接添加到单元格cj中的查询列表FLj；对于被查询范围sqi部分覆盖的单元格cl，对该单元格中四叉树Tl从上至下进行层次遍历，查找被sqi完全覆盖的四叉树节点ni，在节点ni中记录qi，并停止对ni孩子节点的处理（4）～9）行）。如果四叉树Tl中某节点nj与查询范围sqi部分相交，则进一步遍历nj的孩子节点，直至叶子节点（11）～14）行）。根据qi的插入原则，在四叉树Tl中记录qi的所有节点中，只有叶子节点可能与sqi部分相交。因此，如果Tl的某个非叶子节点记录qi，则该节点区域内所有移动对象均被sqi覆盖。

算法2 中，确定与查询qi相交的r个单元格所需时间为T(2n)。假设r个单元格分布在不同的物理计算节点，那么查询qi插入到每个单元格对应的四叉树则可以并行执行，此时，查询qi插入DDI 结构的时间等于单个单元格的最大插入时间。因此，算法2 的时间复杂度可以表示为O(n+(i∈[1，r])。其中，log4mi表示将查询qi插入单元格ci对应四叉树的时间复杂度，四叉树的节点数量为mi。

算法2 添加范围查询至四叉树。

3.3 DDI结构的维护

随着移动对象和范围查询点的位置变化，需要对DDI 进行实时维护，下面本文分别从移动对象的维护和范围查询的维护这两种角度进行讨论。

3.3.1 移动对象的维护

需要注意的是，上述过程中在更新单元格ci对应的四叉树Ti时，需要根据以下情况进行处理：

1）若因oj的移动导致包含(xj，yj)的叶子节点与其兄弟节点的移动对象数量之和小于阈值α时，则该组叶子节点的所有移动对象由其父节点保存，随后删除该组叶子节点，其父节点变为新的叶子节点。

2）若因oj的移动导致包含的叶子节点中移动对象数量达到指定的阈值α，则该叶子节点进行递归分裂，直至每个叶子节点内移动对象数量小于阈值α。

3.3.2 范围查询的维护

假设查询点qi经过移动后，范围查询区域sqi变为。此时，需要对sqi和相关的单元格内的查询列表根据以下情况进行处理：

1）如果sqi覆盖ci且与ci不相交，则将qi从ci的列表FLi删除。

2）如果sqi覆盖ci且与ci相交，则将qi从FLi删除，并插入单元格ci的列表PLi。

3）如果sqi与ci相交且与ci不相交，则将qi从PLi删除。

4）如果sqi与ci不相交且sq′i覆盖ci，则将qi插入FLi。

5）如果sqi与ci相交且覆盖ci，则将qi从PLi删除，并插入FLi。

6）如果sqi与ci不相交且与ci相交，则将qi插入PLi。

上述单元格ci的维护过程相较于单元格ci相应的四叉树Ti的维护而言，仅维护了Ti的根节点。而四叉树Ti的维护需要自上而下判断查询范围能否覆盖每个节点，并重新插入范围查询，以维护查询列表QLi。

3.4 DDI结构的分布式部署

DDI 结构部署于Master-Worker 范式的分布式计算环境下，该分布式集群由一个EntranceWorker 计算节点、多个IndexWorker 计算节点和多个QueryWorker 计算节点组成。DDI 结构的分布式部署框架如图3 所示。首先，在EntranceWorker 计算节点部署一个全局网格索引（Global Grid Index，GGI）。GGI记录每个单元格的边界以及所有单元格与IndexWorker 的对应关系。一旦移动对象或者范围查询到达EntranceWorker节点，该节点将根据GGI确定移动对象和范围查询相关的单元格，并将其分发至对应的IndexWorker。相对于GGI，IndexWorker 计算节点部署一个局部网格索引，对负责区域的单元格、四叉树及其中移动对象索引。每个IndexWorker 根据移动对象和范围查询的插入算法将其插入对应的单元格及其四叉树索引中，并将计算结果发送至QueryWorker，由QueryWorker返回最终结果。

4 面向移动对象范围查询的分布式查询算法

本章首先描述面向移动对象范围查询的DSA，然后介绍面向并发查询的共享计算优化策略，最后阐述移动对象和范围查询位置在连续变化情况下的分布式增量查询算法。

4.1 面向范围查询的分布式查询算法流程

面向移动对象范围查询的DSA是基于DDI结构提出的，算法流程如图3 所示。对于查询qi，EntranceWorker 节点首先根据GGI结构确定查询qi的候选单元格集合Gi，并将查询qi和集合Gi发送至QueryWorker，其中查询qi被插入有效查询列表。此后，由该QueryWorker维护查询qi。然后，EntranceWorker 节点通知维护候选单元格的多个IndexWorker并行查找各自负责单元格中被qi的查询范围sqi所覆盖的移动对象。在该查找过程中，如果某个候选单元格被sqi覆盖，则该单元格内所有移动对象均属于qi的查询结果；否则，自上而下遍历候选单元格所对应的四叉树，可快速找到与sqi相交的区域，并计算得到该单元格内属于qi的移动对象。每个IndexWorker计算得到自身负责的候选单元格中属于qi的移动对象后，将查询结果发送至QueryWorker，QueryWorker只接收有效查询列表维护查询的部分查询结果。QueryWorker每收到一个计算节点发送的部分查询结果，就根据集合Gi判断是否所有候选单元格的结果均已收到。如果均已收到，则返回qi的最终查询结果。

图3 DDI结构的分布式部署框架Fig.3 Framework of distributed deployment of DDI structure

4.2 并发查询共享计算优化计算策略

1）传输代价优化。众所周知，分布式环境下相同规模数据的网络传输开销远远大于CPU 计算代价。当IndexWorker获得不同查询的查询结果后，需要将查询结果发送到维护这些查询的QueryWorker。此时，QueryWorker 数量越多，网络传输代价越大。为解决这个问题，本文采取的策略是将查询范围重叠较多的多个范围查询路由至同一个QueryWorker 进行处理，即负责处理这些范围查询的IndexWorker 需要将查询结果发送至同一个QueryWorker。具体而言，对于两个范围查询qi和qj，EntranceWorker 计算节点根据GGI 计算qi和qj的候选单元格集合分别为Gi和Gj，然后计算集合Gi和Gj的Jaccard 相似度如果δ大于等于指定的阈值，则将qi和qj发送至同一个QueryWorker 处理，否则将qi和qj发送至不同的QueryWorker 处理。

2）查询代价优化。对于与单元格cj部分相交的范围查询qi，在遍历单元格cj对应的四叉树Tj计算qi的查询结果时，一旦发现四叉树Tj的某个非叶子节点被qi对应的查询范围sqi完全覆盖，为得到属于该节点的移动对象，仍需继续向下遍历，直至叶子节点。由于同一单元格很可能与多个范围查询部分相交，范围查询需要对同一四叉树进行多次遍历。这不仅需要做大量重复计算而且耗时较大。为解决这一问题，本文在每个单元格中引入一个基于“二分图”的查询结果索引（Bipartite Graph Index，BGI）结构。

如图4（a）所示，BGI 的结构包含查询集合Qs、四叉树节点集合Ns以及每个四叉树节点对应的移动对象集合Os。对于新到达的查询qi，从单元格cj对应四叉树Tj的根节点开始遍历，假定Tj的某个节点ni被sqi完全覆盖，如果该节点查询列表QLf已有查询qj，则在BGI 的Qs集合中查找qj，然后根据qj在Ns集合中所对应的节点中寻找ni。此时，ni的移动对象集合Os已确定，无需遍历ni的孩子节点；否则，继续遍历ni的孩子节点，获得ni的移动对象集合Os。然后，将qi添加至Qs集合，ni添加至Ns集合。此后，若某个查询的查询范围覆盖节点ni，则可直接从BGI 的Ns集合中获取ni的移动对象。

具体而言，如图4（b）所示，假定已有范围查询sq1覆盖节点n1，n8，且查询点q1、所覆盖四叉树节点以及其中移动对象集合已插入BGI。此时，新的范围查询sq2与sq1覆盖同一节点n8，则查询q2关于n8的查询结果可以从Ns集合中取得。而sq2覆盖节点n2及其所对应的移动对象集合在计算结果后存储于BGI 中（如图4（a）所示）。

图4 BGI结构Fig.4 BGI structure

4.3 分布式增量查询算法

对于已经计算得到初始结果的连续范围查询，本文需要根据移动对象和查询点位置的变化，每隔Δt时间段，对其查询结果进行更新，直至查询失效。为此，本文提出一种增量查询策略，在充分利用已有结果的基础上，对查询结果进行增量更新。下面分三种情况对增量查询策略进行讨论。

1）移动对象位置变化而查询点固定不变。经过Δt时间，位置变化的若干移动对象会向EntranceWorker 节点报告移动前的位置和当前最新位置，根据GGI，EntranceWorker 节点确定需要对其所属移动对象进行更新的单元格集合G，并通知对应的IndexWorker。由IndexWorker 对单元格集合G中的移动对象进行更新。如果一个移动对象是在同一单元格cm中发生位置变化，那么对FLm列表中的查询并无影响，仅需要对PLm中的查询进行更新。在对PLm中的查询进行更新的过程中，可根据单元格cm中的BGI 索引结构，对PLm中的多个查询同时更新。也就是说，在移动对象位置变化而查询点固定不变的情况下，若BGI 索引结构中Ns集合中任意节点ni的移动对象集合发生变化，则根据ni的查询列表QLi，对BGI 查询集合Qs中查询点的查询结果进行更新。

2）移动对象位置固定而查询点位置变化。假设查询qi经过移动后，查询范围由sqi变 为。当qi到 达EntranceWorker 节点后，EntranceWorker 节点分别根据sqi和计算qi上一时刻和当前时刻的候选单元格集合Gl和Gc。如果单元格ck属于Gl但不属于Gc，则维护ck的IndexWorker（IWk）通知负责qi的QueryWorker（QWi）从qi上一时刻查询结果中删除属于ck的移动对象；如果单元格ck不属于Gl但属于Gc，则IWk通知QWi将属于ck的移动对象添加至qi上一时刻的查询结果中；如果单元格ck既属于Gl又属于Gc，则根据以下规则对ck进行处理。

如果(sqi⊆ck) &&(⊆ck)，qi查询范围一直覆盖单元格ck，无需做任何更新。

如果(sqi⊂ck) &&(⊆ck)，将qi从PLk删除并插入FLk。IWk根据四叉树Tk计算(ck-(ck∩sqi))区域的移动对象，并将这些移动对象发送给QWi，QWi则将这些移动对象添加至qi的查询结果。

如果(sqi⊆ck) &&(⊂ck)，将qi从FLk删除并插入PLk。IWk基于四叉树Tk计算(ck-(ck∩))区域的移动对象，并将这些移动对象发送给QWi，QWi则将这些移动对象从qi的查询结果中删除。

如果(sqi⊂ck) &&(⊂ck)，IWk则基于四叉树Tk分别计算被区域(sqi-(sqi∩))和(-(sqi∩))分别覆盖的移动对象集合Od和Oa，然后通知QWi从qi上一时刻的查询结果中删除集合Od中的移动对象，并添加集合Oa的移动对象。

4.4 移动对象和查询点位置变化的增量查询语义。

根据位置不断变化的移动对象和查询点，对查询结果进行增量更新时，EntranceWorker 创建两个队列分别缓存位置变化的移动对象和查询点。当移动对象和查询点位置发生变化后，将被分别插入到移动对象缓存队列和查询点缓存队列。如果查询缓存队列非空，则每隔Δt时间，处理该队列中的查询。在处理查询时，基于当前DDI 结构中移动对象的快照增量更新查询结果；在查询处理过程中，暂停处理缓存队列中位置变化的移动对象。待查询处理完成后，再对缓存队列中位置更新的移动对象进行处理，更新DDI 结构。在此过程中，如果有新的查询或者位置变化的查询到达，则被插入缓存队列，待移动对象处理完成后，在下一个Δt时刻，对新到达的查询进行处理。根据该语义，当移动对象和查询点的位置同时发生变化时，本文将其看作两个独立的事件并在时间维度上将其序列化，两个事件被序列化的先后顺序并不会对查询结果产生实质性影响。然后，将位置变化的移动对象和查询点分别插入两个缓存队列，便可根据上述给定的查询语义进行处理。

4.5 查询算法时间复杂度

对于查询范围为sqi的查询qi，其处理过程包含初始查询和增量查询两个阶段，现分别分析初始查询的时间复杂度和增量查询的时间复杂度。

在初始查询阶段，假设与sqi部分相交的候选单元格数量为r，且这些候选单元格分布在不同的物理计算节点。根据本文的分布式查询思想，可以并行搜索每个候选单元格。此时，初始查询时间等于单个单元格的最大搜索时间。为便于表述，假设候选单元格ci对应四叉树的节点数量为mi，确定被sqi完全覆盖和与sqi部分相交的四叉树节点的时间为T(log4mi)。进一步假设被sqi完全覆盖的四叉树节点数量为，则与sqi部分相交的四叉树节点数量为（），且均为叶子节点。对于每个被sqi完全覆盖的四叉树节点，它所包含的移动对象全部被sqi覆盖，故处理该部分四叉树节点的时间为T(m′i)；对于与sqi部分相交的每个四叉树叶子节点，需要遍历其包含的所有移动对象以判断被sqi覆盖的移动对象，故搜索该部分叶子节点的时间为T(*no)，no为每个叶子节点包含移动对象的平均数量。因此，一个单元格搜索时间为，而初始阶段的时间复杂度为

增量查询分为：

1）移动对象位置变化而查询点位置固定。由于每个候选单元格中被sqi覆盖的个四叉树节点、与sqi相交的个四叉树节点已确定，因此，只需要搜索与sqi相交的每个四叉树节点中新增的移动对象被sqi覆盖即可，所需时间为为新到达与sqi相交的每个四叉树节点中移动对象的平均数量。因此，该情形下增量查询的时间复杂度为

2）查询点位置变化而移动对象位置固定。由于查询点位置变化，需要重新确定候选单元格，时间为T(2n)。此时，假设与sqi部分相交的候选单元格数量仍为r，则该情形下的时间复杂度为虽然该情形下的时间复杂度与初始查询的时间复杂度相同，但是此时m′i和m″i的值要明显小于其在初始查询时的值，故查询效率仍有明显提高。

5 实验与结果分析

5.1 实验配置

本文选择移动对象不同分布的数据集进行实验来评估DDI结构。基于德国路网模拟3个移动对象数据集：均匀分布（Uniform Distribution，UD）数据集、高斯分布（Gaussian Distribution，GD）数据集、齐普夫分布（Zipf）数据集。为了模拟这些数据集，首先将覆盖每个路网的二维空间归一化为一个1×1的正方形区域，并将其划分成100×100个大小相同的单元格，然后根据每个单元格移动对象出现的概率密度分布函数计算每个单元格所分配的移动对象数量，最后令每个单元格内的移动对象在对应的局部路网上以速度vo移动。下面以GD为例阐述数据集的生成过程。由于GD 中的移动对象oi坐标(xi，yi)在x维与y维都满足高斯分布，因此，移动对象oi位于(xi，yi)的概率为即所有移动对象在整个查询区域的概率密度分布函数，其中μ1、μ2、σ1、σ2、ρ分别设为0.5、0.5、0.2、0.2、0。此时，一个移动对象位于第i行、第j列单元格的概率为f(i，j)=0.08π exp[2(xi-0.2)2+2(yi-0.2)2]，其中i，j满足0 ＜i≤100，0 ＜j≤100 且为正整数。假设移动对象总数为No，那么第i行、第j列单元格中的移动对象数量应为f(i，j)*No。然后，在该单元格中产生对应数量的移动对象，令其在该单元格覆盖的局部路网上连续移动。

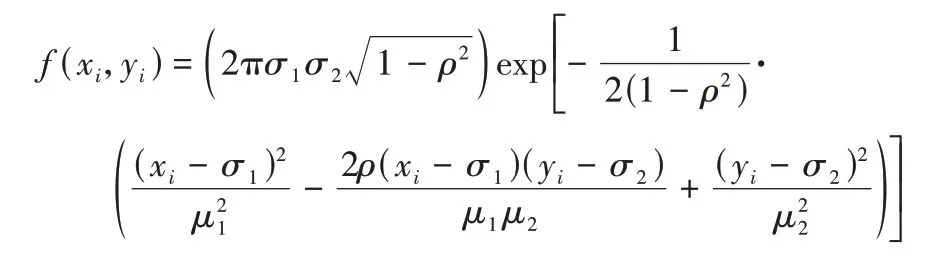
本文引入了3 种分布式算法作为基准方法，以对比评价DSA 的性能。第1 个基准算法NS（Naive Search）不使用任何索引，每个计算节点包含所有移动对象，每个查询被随机分配给所有计算节点；第2 个基准算法GI（Grid Index）是构建一个面向移动对象的分布式网格索引，基于分布式网格索引将给定的查询分配到相应的计算节点，进而多个计算节点并行计算给定查询的查询结果；第3 个基准算法分布式混合索引（Distributed Hybrid Index，DHI）是Yu 等［3］提出的一种全局网格和R-tree 结构组成的混合索引，该算法在分布式网格索引的基础上，以移动对象初始位置为叶子节点建立R-tree，并通过改变叶子节点大小调整索引粒度。

实验的服务器集群是由阿里云租赁的20 个弹性云服务器（Elastic Cloud Server，ECS）计算节点构成，每台服务器为4核16 GB 内存。实验中，DDI 与DSA 所涉及的参数如表2所示。

表2 实验中所涉及的参数以及含义Tab.2 Related parameters and their meanings in experiments

5.2 移动对象DDI的性能评估

5.2.1 移动对象数量对DDI构建时间的影响

在该组实验中，设置一个用以缓存待处理移动对象的队列Qo，将移动对象一次性输入其中，并统计为这些移动对象构建DDI 结构的时间，结果如图5（a）所示。可以看出，DDI构建时间与移动对象数量基本呈同比例增长。此外，处理GD 和Zipf 分布移动对象的时间略高，原因是当移动对象分布密集时，集群中的某些服务器需要处理比其他服务器更多的移动对象，导致这些服务器的负载偏高，影响DDI 结构的整体性能。

5.2.2 阈值α对DDI构建时间的影响

阈值α对DDI 构建时间的影响如图5（b）所示。可以看出，无论移动对象符合哪种分布，随着阈值α增加，索引DDI的构建代价明显减少。原因是阈值α与四叉树的层数直接相关，随着阈值α增大，四叉树分裂子节点的可能性越低，进而四叉树层数减少，使得DDI 的构建代价越少。

图5 不同参数对DDI构建时间的影响Fig.5 Influence of different parameters on DDI building time

5.2.3 移动对象的移动速率对DDI维护时间的影响

该组实验首先为5×107个移动对象建立DDI 结构，然后随机选择5×106个移动对象，令这些被选择的移动对象以不同速率（vo）移动5 次，测试DDI 的平均维护时间，实验结果如图6 所示。可以看出，随着移动对象速率的增加，维护成本明显增加。这是因为当移动速率较低时，移动对象的上一次位置和当前位置有可能位于四叉树的同一叶子节点中，此时不需要对四叉树索引结构进行调整；但当移动对象的移动速率较高时，四叉树节点需频繁调整移动对象数量，导致维护代价增大。

图6 vo对DDI维护时间的影响Fig.6 Influence of vo on DDI maintenance time

5.2.4 DDI的吞吐量

对DDI 的吞吐量测试结果如图7 所示。该组实验中，设置一个队列Qo缓存待处理的移动对象，其容量设置为5×104，令移动对象以不同的速率进入队列Qo，经过一段时间后，检测队列Qo中的移动对象数量（No）。在速率小于4×106移动对象（Objects Per Second，OPS）时，队列Qo内移动对象数量保持平缓。在速率达到4×106OPS 时，队列Qo内移动对象数量迅速增加，即DDI 的吞吐量约为4×106OPS。这说明DDI 可以胜任大规模移动对象的范围查询工作。

图7 DDI的吞吐量Fig.7 Throughput of DDI

5.3 DSA的性能评估

5.3.1 阈值α对DSA查询时间的影响

本组实验测试阈值α的同一组查询的查询时间，实验结果如图8（a）所示。可以看出，随着阈值α的增加，搜索时间先减少后增长，阈值α为15 时效果最优。当阈值α过小时，四叉树索引粒度普遍减小，遍历时间开销相对较大，导致整个查询代价增大；反之，当阈值α过大时，四叉树的索引粒度普遍增大，剪枝效力下降，导致查询时间增长。

5.3.2 搜索范围对DSA查询时间的影响

本组实验首先建立100×100 的DDI（这里定义每个单元格的大小为0.01×0.01），随后评估了DSA 的性能与查询的搜索范围之间的关系，结果如图8（b）所示。可以看出，查询范围的大小对DSA 的性能有一定的影响。一个查询点的查询半径（r）越大，所涉及的候选查询单元格数量越多，即使DSA 能够利用多个计算节点对候选单元格的移动对象进行并行查询，随着候选单元格数量的增大，系统需要处理的计算节点数量也相应增多，而这些计算节点都需要与QueryWorker 进行通信，最终导致DSA 的查询时间增大。

图8 不同参数对查询时间的影响Fig.8 Influence of different parameters on query time

5.4 四种分布式算法的比较

5.4.1 不同数量的范围查询时间比较

本组实验设定不同数量的范围查询，以测试4 种算法的查询时间，实验结果如图9（a）所示。可以看出，DSA 的性能总是优于NS、GI 以及DHI。这是因为NS 在处理每个查询时，所有服务器都使用暴力搜索模式，这使得其查询时间随着连续范围查询的数量呈线性增长趋势；GI 在处理同一组连续范围查询时，由于缺少四叉树索引的支持，需要比DSA检测更多的移动对象；DHI 在处理查询过程中，由于没有考虑查询区域重合率较高的查询存在，可能将其分配到了不同的服务器，造成额外的计算开销；而DSA 不仅考虑了传输代价优化，而且采用BGI 结构使得多个范围查询无需对四叉树底层遍历。

5.4.2 大规模移动对象的查询时间比较

本组实验设定不同数量的移动对象，以测试4 种算法性能所受影响。在该组实验中，一次性向Qq输入104个连续范围查询，4 种算法处理所有查询的时间如图9（b）所示。随着查询数量的增加，NS 的查询时间呈线性增长，而GI、DSA 以及DHI 的性能几乎不受影响。这是因为NS 需要扫描所有移动对象来处理每次查询，而GI、DSA 以及DHI 可以有效地对搜索空间进行修剪，即使移动对象的数量急剧增长，也只需要处理有限的移动对象数量。DSA 与DHI 性能明显优于GI，这是因为DSA 与DHI 分别引入了四叉树索引和R-tree 索引，能进一步提高索引效率，有效处理大规模移动对象范围查询。

图9 4个算法的初始查询时间的比较Fig.9 Comparison of initial query time among four algorithms

5.4.3 增量连续查询的处理时间比较

本组实验中，向Qq一次性输入2 000 个范围查询，令其随机移动，然后测试4 种方法的增量查询时间，实验结果如图10 所示。在实验中，记录了在5 个连续的时间点上用4 种方法处理这些查询的时间。可以看到DSA 的性能优于其他3 种方法，尤其是在最后4 个时间点上。NS 和GI 把每次范围查询作为新的查询，增量查询时间基本不变；DHI 未考虑多个并发范围查询之间的共享计算问题，从而进行冗余的计算；而DSA 每次只需计算每个查询的增量结果，有效降低了增量查询时间。

图10 增量查询时间比较Fig.10 Comparison of incremental query time

5.4.4 不同算法的吞吐量比较

本组实验通过计算连续范围查询的初始结果来评估3种查询方法的吞吐量。在该组实验中，查询点以不同的速率进入系统，然后更新缓存在Qq中的查询点数量，设置缓存队列Qq容量为104。图11 是DSA、GI、NS 的吞吐量实验结果。从图11（a）中可以看出，当速率（vq）不大于4 000 OPS 时，Qq的占用容量一直较小，但当速率（vq）达到5 000 OPS 时，其占用容量开始明显增加。因此，DSA 的吞吐量约为4 000 OPS。从图11（b）、（c）中可以看出，GI 和NS 的吞吐量分别约为3 000 OPS 和1 000 OPS，均小于DSA。这说明DSA 能够很好地在分布式集群上处理大规模移动对象连续范围查询。

图11 DSA、GI、NS的吞吐量Fig.11 Throughput of DSA，GI，NS

6 结语

本文提出了一种由网格索引与弹性四叉树组成的移动对象分布式索引结构DDI，该结构能够提供高效的剪枝效力，具有较低的维护代价且易于部署到分布式服务器集群，具备良好的可扩展性。基于该索引结构，本文进一步提出了分布式增量连续查询算法，该算法设计了面向高并发查询的共享计算策略以及面向连续范围查询的增量查询策略，能有效降低查询代价。最后，通过大量实验对本文方法的性能进行了充分验证。

本文提出的移动对象分布式索引结构DDI 主要处理基于欧氏距离的范围查询，未来将进一步研究基于路网的移动对象分布式范围查询算法。