单螺栓连接梁的非线性连接层建模与参数识别
刘鹏韬,关天赐,王小鹏
(西安交通大学 机械工程学院,西安 710049)
螺栓连接广泛存在于各种机械设备,但是其结合面处的复杂机理通常会导致螺栓连接处存在能量耗散、刚度软化以及局部阻尼增大的非线性动力学现象。以航空航天设备为代表的重大复杂设备需要有足够精确的模型来描述其动力学特性,然而螺栓连接引发的非线性使得上述问题不易解决。对螺栓结合面的精准建模是解决问题的关键。为了刻画螺栓连接处的动力学特性,相关研究者提出和改进了多种模型。
Gaul等[1]通过试验发现螺栓结合面处有三种运动状态,在轻微载荷作用下,结合面从黏着状态进入微观滑移状态;载荷增加至某一定值后,微观滑移状态转变为宏观滑移状态。针对螺栓结合面的非线性行为,Iwan模型由于其参数具有一定的物理意义,被广泛地应用于结合面的建模[2-4]。Iwan单元由Jenkins单元并联而成,每个Jenkins单元由弹簧和滑动摩擦阻力片串联而成,其模型示意如图1所示。为了提高Iwan模型的精度,Segalman[5]提出了一种4参数的Iwan模型,用幂函数来描述其滑移力分布特性;Li等[6-8]将Iwan模型改进为六参数模型,根据连接结构恢复力和位移迟滞曲线来识别模型参数。王东等[9]将Iwan模型应用至螺栓结合面,对激励力幅值引起的结合面非线性行为进行了探究。但是Iwan模型依赖于参数识别方法以及识别准确度,且具体结构只能具体分析,泛用性较差[10]。

图1 Iwan模型Fig.1 Iwan model
表征螺栓结合面特性的另一种常用手段是在结合面之间建立薄层单元。薄层单元模型示意如图2所示。Iranzad等[11]使用具有弹塑性的薄层单元来表征螺栓接合面的非线性行为,薄层单元的四个参数通过最小化测试与预测的频响函数之差来确定。Chu等[12]使用双线性本构关系的薄层单元来揭示螺栓结合面的非线性特性,但是用双线性本构关系描述结合面非线性的方法不够精确。Alamdari等[13]使用Richard-Abbot本构关系的薄层单元描述螺栓结合面在剪切载荷下的非线性行为。Zhan M[14]使用薄层单元表征螺栓连接界面,薄层单元的线性参数通过贝叶斯推理的分层模型进行识别,识别完成后可以计算模态频率。薄层单元的存在改变了连接结构的尺寸和质量,虽能一定程度上表征螺栓结合面处的动力学特性,但实际上不相符于真实情况,并且目前没有明确的研究指导薄层单元厚度的最优选取。

图2 薄层单元模型Fig.2 Thin layer unit model
不同于薄层单元机理,Shokrollahi等[15]提出接触区连接层单元,将其应用在螺栓连接影响区内来刻画螺栓连接处的线性动力学行为。接触区连接层单元不改变螺栓连接部位的厚度和质量,不需要调整整个模型,只需在结合面处做出轻微的变化,对比于其他建模方式有着明显的优势,其示意如图3所示。Adel等[16]在“螺栓影响区”概念基础上提出了螺栓连接区的“双连接层”模型,用于复杂机械结构的连接界面的模态分析。但是该模型只能描述螺栓连接的弹性性能,即对于螺栓结合面的研究局限于线性范围内。

图3 连接层等效模型Fig.3 Equivalent model of connective layer
螺栓连接模型的参数识别方法有多种。Yang等[17]提出了信赖域约束灵敏度方法,从噪声时域响应数据中识别螺栓连接Iwan模型的参数。Zhang等[18]通过基于功率谱的贝叶斯方法来识别螺栓连接的Iwan模型参数。郭宁等[19]通过水循环算法对螺栓连接的薄层单元参数进行全局修正。Yao等[20]基于螺栓连接刚度技术和分形接触理论确定了薄层单元的材料参数,范世荣等[21]通过加权方法推导了结合部各向同性虚拟材料模型的弹性模量和切变模量。李朝峰等[22]基于准静态试验,通过fminsearch无约束非线性优化的方法实现了对所建立螺栓连接界面非线性模型的参数识别。
针对于现有文献,用接触区单元对螺栓结合面进行建模是可行且有优势的,但是其在螺栓连接方面的研究仍停留在线性阶段,无法表征进入微观滑移状态后结合部的动力学行为。另一方面,对于各种螺栓结合部等效模型有诸多方法可以进行参数识别,而鲜有对新提出的连接层等效模型的非线性参数进行识别的方法。为了准确刻画螺栓连接处的动力学特性,揭示其非线性行为,本文将非线性连接层单元应用至单螺栓连接梁处,用遗传算法进行参数识别,更新连接层模型的非线性参数。
1 非线性连接层等效模型及参数识别理论
1.1 连接层理论
连接层理论将螺栓在连接件接触面的影响扩展至被连接件处,所生成的连接层单元由部分被连接件组成,示意图见图3。对于螺栓连接,在忽略切向和法向行为的耦合作用时,其正交各向同性的线弹性本构方程如式(1)所示。
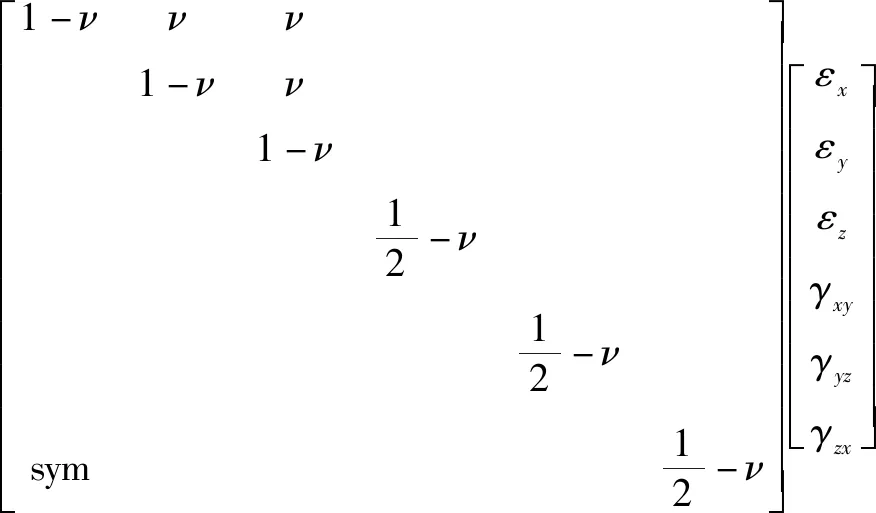
(1)
式中:σi(i=x,y,z)为材料3个主轴方向的正应力;εi(i=x,y,z)为材料3个主轴方向的正应变;τij(i=x,y,z;j=x,y,z;i≠j)为材料的切应力;γij(i=x,y,z;j=x,y,z;i≠j)为材料的切应变E为材料的弹性模量;ν为材料的泊松比。
1.2 Voce塑性阶段的应力-应变关系
根据对非线性薄层单元模型的研究,非线性的弹塑性材料本构关系能够表征结合部的非线性特性。因此,本文在连接层等效模型的基础上,采用改进的各向同性Voce模型描述连接层单元塑性阶段的应力-应变关系。Zhao等[23]改进的Voce模型本构关系如式(2)所示。
σp=Sy+Epεp+R(1-e-nεp)
(2)
式中:σp为塑性应力增量;Sy为初始屈服应力;Ep为切线模量;εp为塑性应变增量;R、n为控制应力应变曲线形状的参数。
这一模型包括4个未知参数:初始屈服应力Sy,切线模量Ep,形状参数R和n。切线模量Ep和初始屈服应力Sy表征结合部的刚度软化特性和摩擦阻尼,形状参数R和n控制Voce模型应力-应变曲线的曲率。对Voce模型的4个参数进行调整,可以模拟结合部从黏着阶段到微观滑移阶段和宏观滑移阶段的运动过程。
1.3 参数识别方法
1.3.1 非线性参数识别
非线性连接层等效模型的材料参数未知,需要进行参数识别。由于有限元模态仿真计算忽略非线性特征,因此本文应用Iranzad等提出的非线性参数识别方法,具体识别流程如图4所示,基本步骤如下:
(1) 在有限元软件ANSYS中对螺栓连接结构进行建模,并在其螺栓结合部建立非线性连接层等效模型,输入初始参数;
(2) 通过非线性瞬态仿真计算得到螺栓连接结构在不同激励频率正弦载荷下的加速度响应;
(3) 根据螺栓连接结构仿真计算得到的加速度响应与试验得到的加速度响应建立目标函数,将非线性连接层模型的材料参数作为设计变量 ;
(4) 设置约束条件,基于遗传算法对非线性连接层模型的材料参数进行识别;
(5) 目标函数满足终止条件后,得到识别后的非线性连接层模型参数。
螺栓连接结构的频响函数能够反映结合部的非线性特性,本文通过不同激励频率正弦载荷下螺栓连接结构的加速度响应构建目标函数。目标函数定义为试验与计算得到的加速度响应差值最小化,如式(3)所示。
(3)
式中:au(ωi)为计算加速度值;ae(ωi)为试验加速度值。
参数识别后的结果通过误差指标Eacc评定其准确性,Eacc为螺栓连接结构试验加速度值和参数识别后计算加速度值之间的误差,如式(4)所示。
(4)
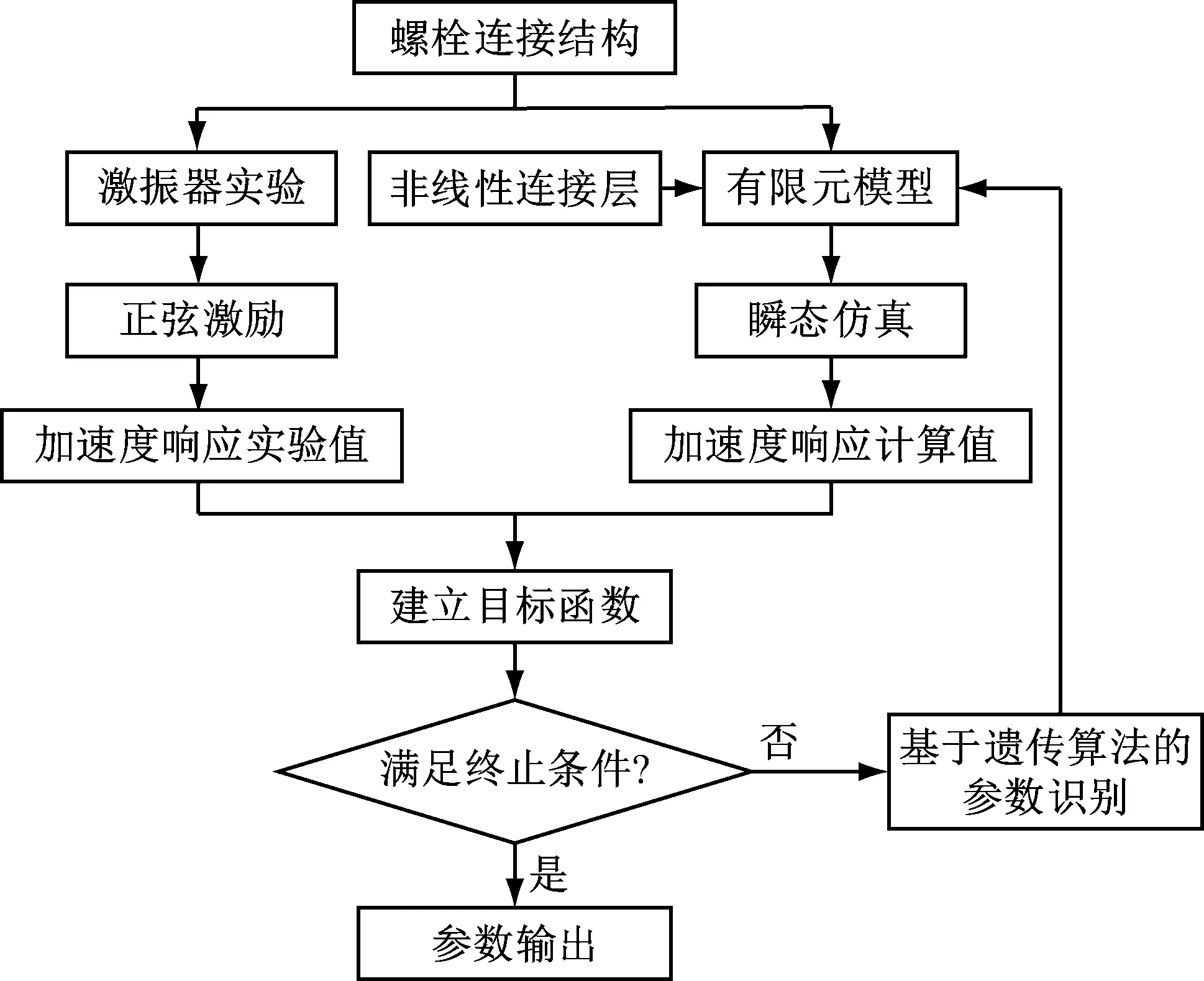
图4 非线性连接层参数识别流程图Fig.4 Flow chart for parameter identification of nonlinear connective layer
1.3.2 线性参数识别
线性参数识别与非线性参数识别过程类似,区别在于其识别过程中目标函数定义为有限元计算与模态试验获得的固有频率差值最小化,如式(5)所示。
(5)
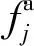
2 单螺栓连接梁试验研究
本文通过单螺栓连接梁结构对提出的非线性连接层等效模型与参数识别方法的可行性进行验证和分析。将两根相同材料和尺寸的钢梁通过M10螺栓连接,连接区域长度为60 mm,整个单螺栓连接梁的几何尺寸如图5所示。

图5 单螺栓连接梁几何尺寸Fig.5 Geometric dimension of single bolt connection beam
为了获得单螺栓连接梁的模态参数,在固定-自由边界条件下对单螺栓连接梁进行锤击法模态试验。将两个加速度传感器(3273A2,DYTRAN)分别安装在单螺栓连接梁表面的B1和B2点,如图6所示,其中螺栓预紧扭矩设置为5。固定加速度传感器后,用力锤(5800B3,DYTRAN)逐个敲击试验测点。每个测点重复测量4次,存储平均频响函数与相干函数。
次年,国子监彭元瑞涉嫌亲戚顶买吏员一案被初彭龄参劾。案件盘根错节,彭托户籍官员朱瀚作假户籍,付好处费160两,随后,找门生冒名顶替受害人严维敬。彭被革去太子少保协办大学士、吏部尚书,降授侍郎南书房行走[7]。这是初彭龄参劾成功的第一例腐败案件。

图6 单螺栓连接梁模态试验设置Fig.6 Modal experiment setup of single bolt connection beam
将梁的厚度方向定义为z轴方向,长度方向定义为x轴方向。由于螺栓连接沿z轴方向,因此主要关注单螺栓连接梁z轴方向的弯曲模态。采用m+p Analyzer软件对z轴方向的试验数据进行模态试验分析,获得单螺栓连接梁的频响函数如图7所示,z轴方向前6阶弯曲模态的试验振型如图8所示。
改变螺栓预紧扭矩,重复试验多次,获得不同螺栓预紧扭矩下单螺栓连接梁的前6阶固有频率如表1所示。从表中可以看出,随着螺栓预紧扭矩的增大,单螺栓连接梁的前6阶固有频率均升高,说明预紧力的大小影响连接结构的模态参数。由于预紧力的增加会使结合部发生接触的微凸体数目增多,接触刚度变大,从而导致连接结构的固有频率升高。当预紧扭矩上升至20 N·m后,继续增大预紧扭矩的大小,单螺栓连接梁的固有频率上升幅度减小并趋于稳定。这一试验现象说明当预紧力增大到一定程度后,预紧力对单螺栓连接梁模态参数的影响明显降低。因此对于螺栓连接结构,可以通过合理调整预紧扭矩的大小改变结构整体的动力学特性,为螺栓连接结构进一步的动力学特性分析和优化设计提供依据。

图7 单螺栓连接梁的频率响应函数Fig.7 Frequency response function of single bolted beam

(a) 第1阶振型
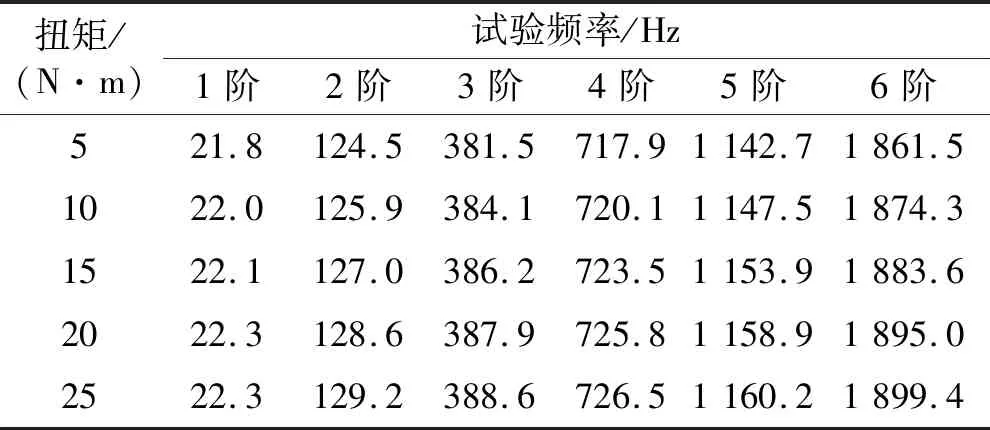
表1 螺栓预紧扭矩下单螺栓连接梁前6阶试验频率Tab.1 The first six experimental frequencies of single bolt connection beams with bolt pre tightening torques
螺栓连接在轻微载荷作用下不产生局部滑移,只表现出线弹性行为,其非线性特性需要在较大幅值的激励力下体现[24-25]。为了研究螺栓结合部的非线性特性,对结构开展激振器法频响函数测试试验。其试验测试系统如图9所示,试验配置主要设备有:激振器、阻抗头、功率放大器、加速度传感器、数据采集仪、安装m+p VibControl振动控制软件的PC机等。
在固定-自由边界条件下,对单螺栓连接梁开展激振器法频响函数测试试验,如图10所示,其中螺栓预紧扭矩设置为10 N·m。通过数据采集仪(m+p VibPilot)中的信号发生器产生正弦信号,经功率放大器放大后驱动电磁激振器(DH40500,DONGHUA)对单螺栓连接梁施加正弦激励。设置正弦激励频率范围为21~23 Hz,在单螺栓连接梁的第一阶固有频率附近。激振力幅值分别为1 N、3 N和6 N,扫频速度为0.4 Hz/min。在载荷施加点粘贴阻抗头(5860B,DYTRAN)以拾取激振器施加于单螺栓连接梁的激振力信号。将两个加速度传感器(3273A2,DYTRAN)分别安装在单螺栓连接梁的B1和B2点,以拾取对应点的加速度信号。数据采集仪采集并记录力和加速度信号,结合m+p VibControl软件实现激振力载荷的闭环控制,以实现激振力幅值在整个测试过程中保持在预设误差范围内(误差范围:预设值±5%)。不同激振力幅值下测点B1测得的单螺栓连接梁的频响函数曲线如图11所示。

图9 激振器法频响函数测试试验系统Fig.9 Frequency response function test system based on vibration exciter

图10 单螺栓连接梁激振器法频响函数测试试验Fig.10 Experimental study on frequency response function of single bolted beam with exciter method
从图11中可以看出,随着激振力幅值的增大,共振峰频率降低,说明螺栓连接结构的固有频率和结合部刚度会随激振力幅值的增加而降低,说明结合部具有刚度渐软特性。这是由于激振力幅值越大,结合部发生滑移的微凸体越多,导致结合部接触刚度降低,共振峰频率降低。此外,共振峰的峰值不同,说明结合部具有幅变阻尼特性。在微观滑移阶段,随着激振力幅值增大,结合部发生滑移的微凸体增多,由于微凸体间摩擦造成的能量耗散增加,导致共振峰的峰值降低。
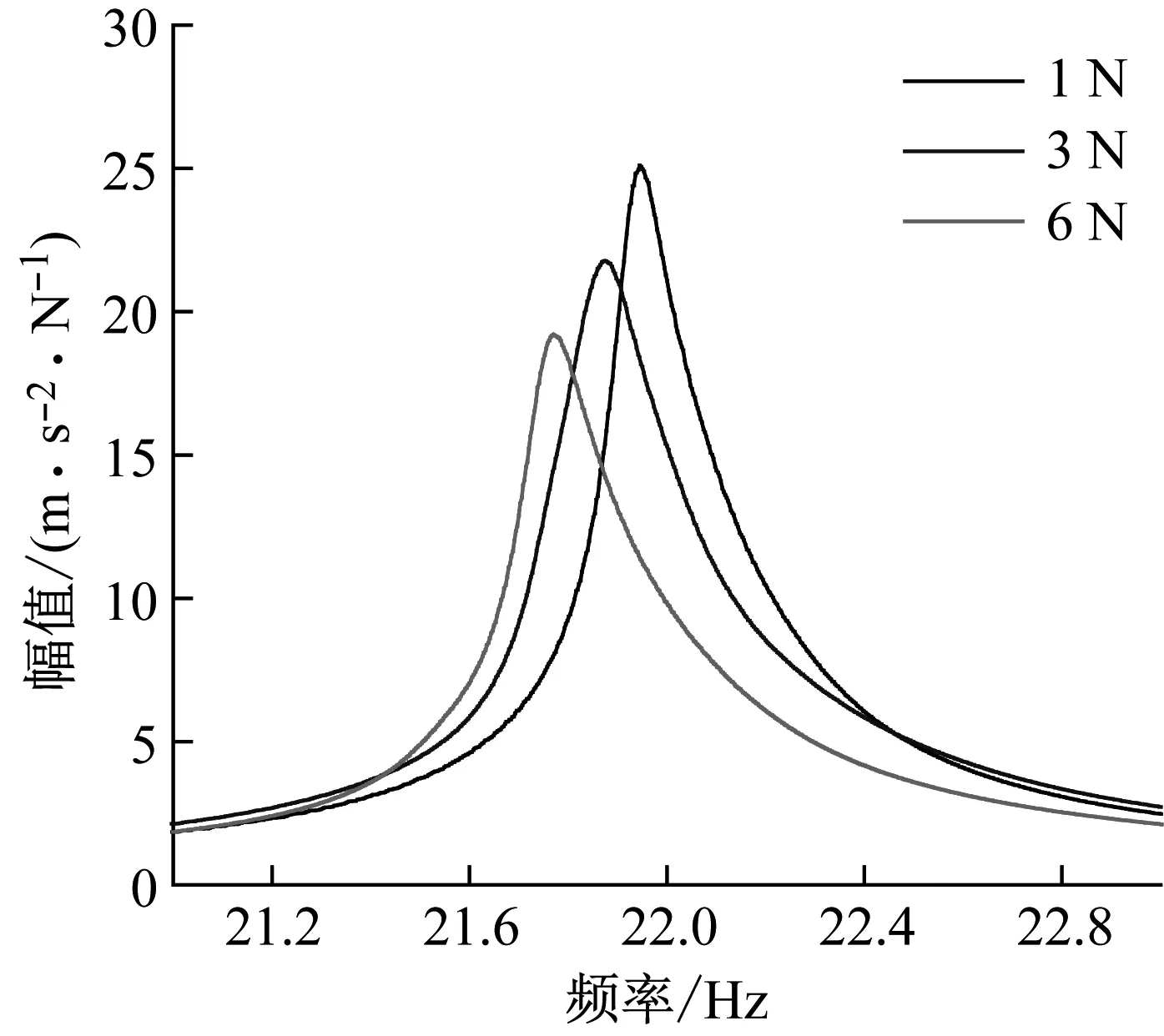
图11 不同激振力幅值下单螺栓连接梁的频率响应函数Fig.11 Frequency response functions of single bolted beam with different excitation force amplitudes
3 参数识别
3.1 模型线性参数识别
在非线性连接层等效模型中,应力大小未达到初始屈服应力前,连接层处于线弹性阶段。因此需要进行线性参数识别。首先在有限元软件ANSYS中建立单螺栓连接梁的连接层等效模型,由于该模型将连接层扩展至被连接梁内,所以将梁的共同接触部分建立为连接层。连接层与被连接梁之间定义为绑定接触。连接层的厚度依据薄层单元模型的研究结果进行选取,当连接薄层长度与厚度比值为10~100时能取得较为准确的结果[26]。因此,在连接层等效模型的长度与厚度比值范围内,为方便计算,本文将非线性连接层厚度设置为6 mm。将连接层定义为各向同性线弹性材料。螺栓、螺母与垫圈(36g)简化为集中点质量。所建立有限元模型如图12所示。

图12 单螺栓连接梁的有限元模型Fig.12 Finite element model of single bolt connection beam
被连接梁的材料为45钢,弹性模量为205 GPa,泊松比为0.3,密度为7 850 kg/m3。初始仿真中非线性连接层模型的线性材料参数如表2所示。模型中被连接钢梁与连接层均使用20个节点的三维单元(solid186),包括4 872个单元与29 419个节点。为了与试验中的约束条件一致,被连接钢梁1的左端面设置为固定约束。此外,在仿真模型的y轴方向定义零位移约束,该约束可以避免模型的横向弯曲(y-x平面内)与扭转模态,保证在改变设计参数时不改变振型的阶数[27]。
仿真计算得到单螺栓连接梁的前6阶弯曲模态振型如图13所示。从图中可以看出,单螺栓连接梁前6阶仿真振型与图8中的试验振型一致。在振型一致的前提下,按照式(5),将在预紧扭矩为10 N·m时前四阶固有频率的试验值和仿真计算值的最小化差值作为遗传算法的目标函数。连接层模型的线性材料参数设置如表2所示。遗传算法每迭代一次,将迭代之后的弹性模量和泊松比更新至连接层模型处,不满足终止条件则继续迭代。终止条件设定为
(6)
材料参数的初始值及变化范围如表2所示。

表2 非线性连接层线性材料参数初始值与变化范围Tab.2 Initial value and variation range of linear material parameters of nonlinear connective layer

(a) 第1阶振型
目标函数迭代收敛过程如图14所示,从图中可以看出目标函数经过21次迭代后收敛,每次迭代计算20个设计点。参数识别后非线性连接层的线性材料参数如表3所示,单螺栓连接梁模态仿真计算的固有频率如表4所示。从表4中可以看出,识别后单螺栓连接梁的前4阶计算频率与试验频率之间的误差均小于1.5%,未参与识别过程的第5~6阶固有频率误差同样小于1.5%,验证了参数识别的准确性。
3.2 模型非线性参数识别
为了识别非线性连接层等效模型的非线性材料参数,通过ANSYS有限元软件对单螺栓连接梁进行瞬态动力学仿真计算。有限元模型与前文中相同,其中非线性连接层塑性阶段特性被定义为Voce模型本构关系。仿真中激励点与测点的位置与试验相对应,通过计算获得单螺栓连接梁的加速度响应值。

图14 目标函数迭代收敛图Fig.14 Iterative convergence graph of objective function

表3 非线性连接层线性材料参数识别值Tab.3 Identification value of linear material parameters of nonlinear connective layer

表4 参数识别后单螺栓连接梁的计算频率Tab.4 Calculation frequency of single bolt connective beam after parameter identification
在幅值为6 N的正弦激励下单螺栓连接梁测点B1的加速度响应中,在以第一阶共振峰为中心,长度为1 Hz的区间内,按0.25 Hz等间隔选取五个频率点,按照式(3)构造遗传算法的目标函数,也即式(3)中m取值为5。终止条件设定为
(7)
其它幅值下的试验数据用来验证参数识别的准确性,参数初始值与变化范围如表5所示。

表5 非线性连接层非线性材料参数初始值与变化范围Tab.5 Initial value and variation range of nonlinear material parameters in nonlinear connective layer
目标函数迭代收敛过程如图15所示,从图中可看出,目标函数经过29次迭代后收敛,每次迭代计算20个设计点。

图15 目标函数迭代收敛图Fig.15 Iterative convergence graph of objective function
非线性连接层的非线性材料参数识别值如表6所示。通过未参与识别过程的激振力幅值1 N和3 N下的试验数据验证参数识别的准确性。根据表6中非线性连接层的材料参数,分别计算出不同幅值和频率的正弦激励下单螺栓连接梁的加速度频率响应函数值,与试验值进行对比,如图16所示。从图中可以看出,参数识别后单螺栓连接梁频率响应函数的计算值与试验值吻合较好。

表6 非线性连接层的非线性材料参数识别值Tab.6 Identification value of nonlinear material parameters of nonlinear connective layer

图16 单螺栓连接梁频率响应函数试验值与参数识别后计算值对比Fig.16 Comparison of experimental and calculated values of frequency response function of single bolt connection beam
根据式(4)计算不同激振力幅值下单螺栓连接梁频率响应函数的计算值与试验值的误差Eacc如表7所示。可以看出,在不同幅值激振力作用下,参数识别后单螺栓连接梁频率响应函数计算值与试验值误差均控制在10%以内,这表明非线性连接层模型准确性。同样容易看出,误差随着激振力幅值的增加而减小。大幅值的激振力将引起螺栓连接结构的非线性行为,而本文所提出的模型对于大幅值激振力作用下频响函数的误差更小,这意味着该模型对非线性行为的描述更加准确。

表7 参数识别后单螺栓连接梁频率响应函数计算值与试验值误差Tab.7 The error between the calculated value and the experimental value of frequency response function of single bolt connection beam after parameteridentification
4 结 论
本文提出一种非线性连接层等效模型,采用Voce模型描述非线性连接层单元塑性阶段的应力-应变关系。以单螺栓连接梁为研究对象,在螺栓结合部建立非线性连接层等效模型并进行参数识别。主要结论如下:
(1) 通过试验获得了螺栓预紧力和激振力幅值对单螺栓连接梁动力学特性的影响规律。试验结果表明,随着螺栓预紧扭矩的增大,单螺栓连接梁的固有频率升高。当预紧扭矩上升至20 N·m后,继续增大预紧扭矩的大小,单螺栓连接梁的固有频率上升幅度减小并趋于稳定。随着激振力幅值的增大,单螺栓连接梁的共振峰频率降低,共振峰的峰值减小,表明结合部具有刚度渐软特性与幅变阻尼的非线性特性。
(2) 非线性连接层材料的线弹性参数表征螺栓结合部在低振动水平下的线性特性,塑性参数表征结合部的刚度软化特性和摩擦阻尼,形状参数控制应力-应变曲线的曲率。参数识别与更新后的模型可以表征螺栓结合部从黏着状态到微观滑移状态和宏观滑移状态的动力学特征,也即其线性与非线性动力学特性。
(3) 参数识别后不同激振力幅值下单螺栓连接梁频率响应函数的计算值和试验值的一致性较好,误差均在10%以内,表明非线性连接层等效模型能够较为准确地模拟结合部的刚度软化和摩擦耗散的非线性特性。通过应用该模型,能够提高连接结构的建模计算精度。

