热力效应作用下小区风环境风洞试验研究

杨 瑛，胡嘉懿，沈 炼，2，汪 阔，孙 昱，许赤士

(1. 长沙理工大学桥梁工程安全控制技术与装备湖南省工程技术研究中心，湖南长沙 410076； 2. 长沙学院土木工程学院，湖南长沙 410012； 3. 湖南省建筑设计院集团股份有限公司，湖南长沙 410208)

0 引 言

城市风环境是评估小区人居舒适性的重要指标，近年来渐渐成为研究热点，得到了广泛关注[1-3]。随着城市化进程不断推进，热岛效应愈加明显，由城市局部温差引起的热对流不容忽视，如夏季建筑表面温度可高达50 ℃，而目前温度对实际小区风环境的具体影响尚不明确，对其展开深入研究具有重要的现实意义。

温度作用下风场研究的主要手段有数值模拟和风洞试验，何仲阳等[4]采用k-ε湍流模型分析了地表温差对流场的影响，发现在平坦地区，温度对低风速流场影响较大；Cheng等[5]通过大涡模拟(LES)考察了大气热分层下城市街道峡谷的流动特征，揭示了大气热分层对街道峡谷流场的分布规律；Li等[6-8]通过LES研究了地面加热对城市街道峡谷内的流场分布，发现地面加热能加快街道峡谷内流量、湍流和污染物的扩散。通过上述研究发现，当前研究主要集中在街道峡谷和地形流场的机理分析，而对实际小区的针对性分析还非常缺乏。同时，数值模拟由于其计算参数的不确定性，往往需要风洞试验对其进行验证。Chaudhry等[9]利用风洞试验和CFD数值模拟相结合的手段研究了渐近加热对空气非均匀流场的影响，发现逐渐升温会使测试区的速度降低；Uehara等[10]利用风洞试验研究了大气热分层对城市街道内流场影响，发现大气热分层超过某一特定值时街道峡谷内风速几乎为0；Allegrini等[11-12]通过风洞试验揭示了浮力对城市街道峡谷流场的分布规律，发现在低雷诺数时街道峡谷内速度增幅较大；Kovar-Panskus等[13]利用风洞试验研究了迎风面受热对街道峡谷内气流扩散的影响，发现迎风面理查逊数Rb<1时惯性力是影响街道峡谷内空气流动的主要因素；欧阳琰等[14]采用风洞对小区的流场和污染物扩散进行研究，发现污染物浓度受来流风速的影响；Hajra等[15-16]通过试验发现下游建筑高度是影响污染物扩散的主要参数。与数值模拟一样，当前考虑热力效应下的流场风洞试验研究主要集中在街道峡谷、大气分层等领域，这些研究结论为热力条件下的风场分析提供了宝贵试验参数，但不足的是当前风洞试验研究并没有将热力效应直接运用到实际小区的风环境模拟，特别是对不同热力强度下实际小区流场相关性与舒适度影响的定量分析还未见其报道。

针对当前研究的不足，本文将借助大尺寸风洞，对实际小区在不同热力条件下的平均风、雷诺应力、相关性与舒适度等指标进行深入分析，定量揭示热力效应对流场的影响，相关研究结论可为城市规划与小区建筑布局提供参考。

1 风洞试验

1.1 大气边界层风洞

本试验在长沙理工大学风工程与风环境研究中心进行，风洞如图1所示，其试验段尺寸为21 m(长)×10 m(宽)×3 m(高)，转盘直径为5.0 m，风速范围为1.0～18.0 m·s-1，采用变角度叶片控制技术，保证了低速流场品质，同时配备了三维移侧架，可在风洞内监测模型任意位置风速。

1.2 风速测量仪器

试验过程中，人行高度位置处风速采用欧文探针测量，探针结构如图2所示。探头直径为15 mm，在探头中心开槽，槽中心穿插一根直径1 mm中空钢针(A端)，开槽处下端布置另一根直径1 mm的中空钢针(B端)。根据欧文探针原理可知，风速与A、B端的压差呈正比关系，即

(1)

式中：pA、pB分别为探头两端的风压；a、b为探头的标定系数；u为A端的风速。

竖向风速测量采用澳大利亚TFI公司的Cobra探头(眼镜蛇风速仪)，该探头能够同时测量三向压力或风速时程，采样频率为512 Hz，采样时间为1 min。

1.3 加热装置

在风洞模型前铺设电阻丝电热板，模拟地面温度，利用控温数显加热开关设定目标温度，其中，加热开关可调范围为0～60 ℃，测温精度为±1 ℃，最大功率为180 W·m-2。

1.4 试验模型与测点布置

建筑模型的设计与加工遵循相似准则，缩尺比为1∶200，如图3(a)所示。试验前将模型放置于风洞转盘上，模型直径为3.0 m，模型阻塞比约为2%，左右两侧均留有3 m空间，确保试验过程中风洞壁面对流场的影响。试验过程中布置了110个欧文探针，并在典型位置监测风剖面，监测位置如图3(b)所示。

试验时采用均匀风和B类地表风两种入口来流条件，B类风场参照规范[17]模拟的风剖面和湍流度剖面，如图4所示。试验过程中模拟了8个风向角，间隔45°，风向角通过旋转模型角度实现。

1.5 试验工况

近地面流场会因为温度分布不均匀产生浮力，而理查逊数可用来评估浮力对流场的影响。大气湍流理论中，理查逊数Rb是湍流运动抵抗重力所做功与雷诺应力产生平均动能转变成脉动动能的比值，理查逊数越大，表示浮力的影响越重要。假设高度h0处温度与地面温度差值为ΔT，高度h0处的风速为u0，g为重力加速度，T0为环境温度，理查逊数Rb可表示为

(2)

为了有效地获取地面加热对流场的影响，利用理查逊数Rb表征热力效应，采用不同Rb数对空风洞进行了详细分析，通过眼镜蛇风速仪测得风速发现，测量高度超过0.5 m以后，温度对风速影响几乎可以忽略，因此本文h0取0.5 m，环境温度T0取20 ℃，均匀流u0为1.2 m·s-1。试验过程中，利用欧文探针捕捉人行高度2 m位置的平均风速，并利用Cobra风速仪对典型位置风剖面进行了详细监测，监测风剖面如图5所示。试验过程中，通过改变加热板的温度，得到了5种工况下的Rb数[18]，分别为0、-0.07、-0.17、-0.28和-0.38，采用3次温度测量的平均值作为最终试验值，以确保试验精度。

2 热力效应下空流场分布机理

为揭示温度场对流场的影响规律，采用平均风进行风洞试验研究。对上述5种不同工况进行试验，获取不同工况下测点的风速时程。同时，对不同Rb数作用下测点顺风向速度分布以及雷诺剪切应力分布进行详细分析，其结论如下所述。

2.1 平均风

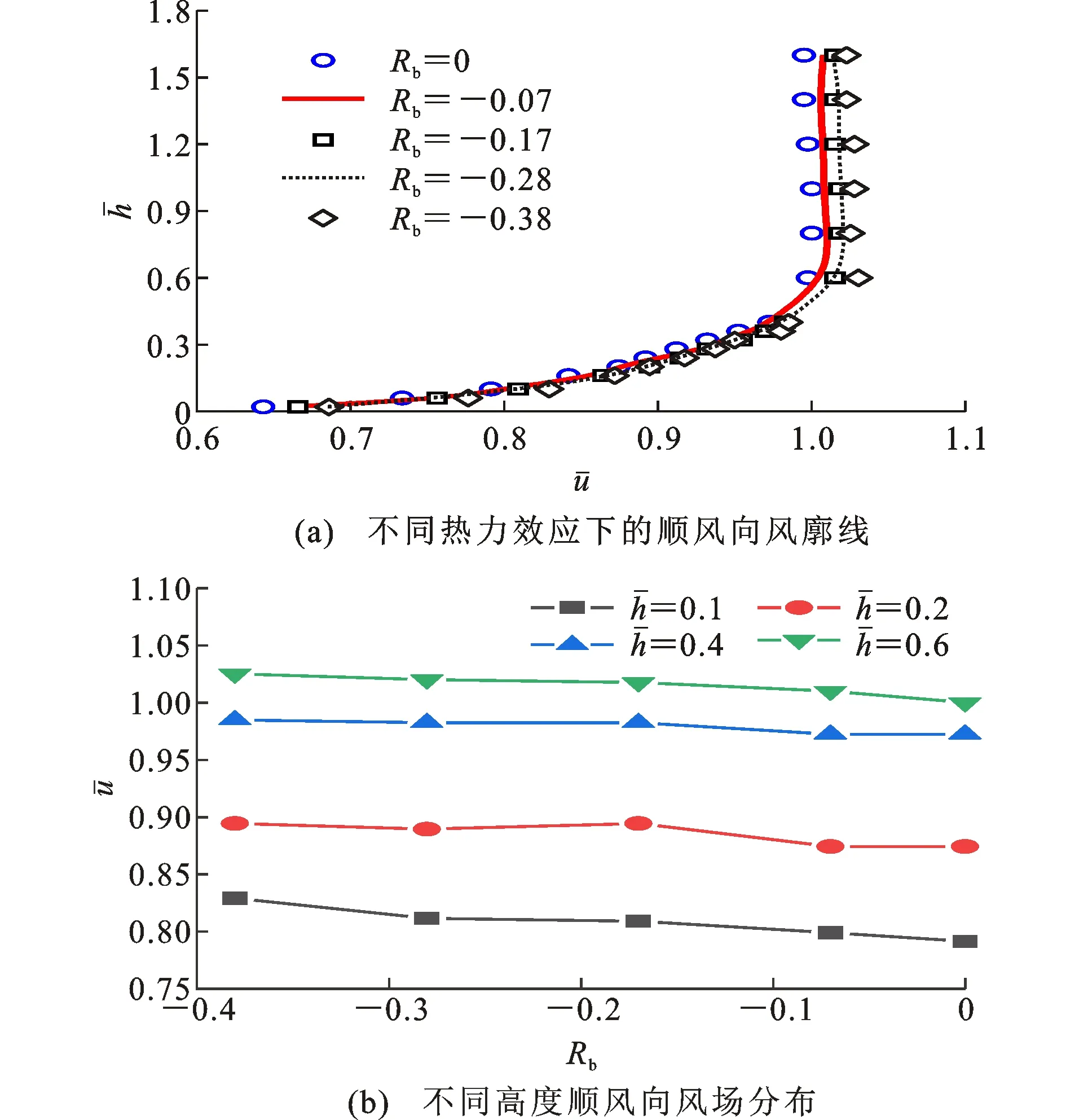
2.2 雷诺剪切应力

3 热力效应下的小区流场分布

3.1 整体风速分布

研究显示，当雷诺数达到临界值后，流场的分布不随入口风速的变化而变化，即在对应某一风向下建筑物周围流场是相对固定的，定义风速比MVR为

(3)

式中：ui为i号测点行人高度风速。

通过风洞试验得到了在不同风向角下该小区人行高度风速分布，本文仅展示主导风向在Rb=0、Rb=-0.17和Rb=-0.38下的人行高度风速云图，图9和图10分别为平均来流和B类入口来流作用下人行高度风速云图。从图9、10发现，两种来流作用下的小区流场分布大致相同，均形成了很明显的“峡谷效应”，主要原因是小区建筑物与山体之间间距很小，出现了局部强风，而在建筑物背风面出现大量低风速区。

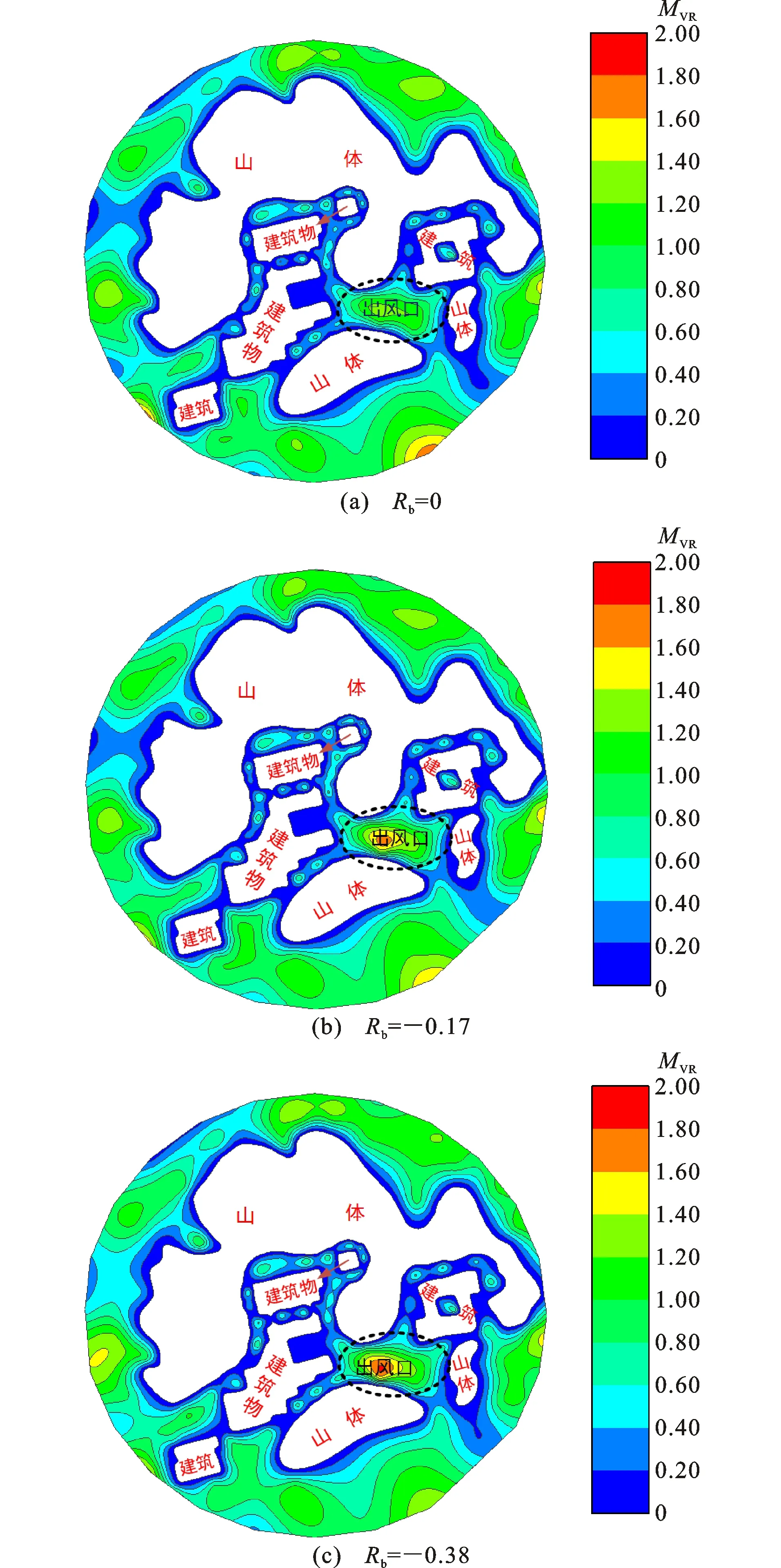
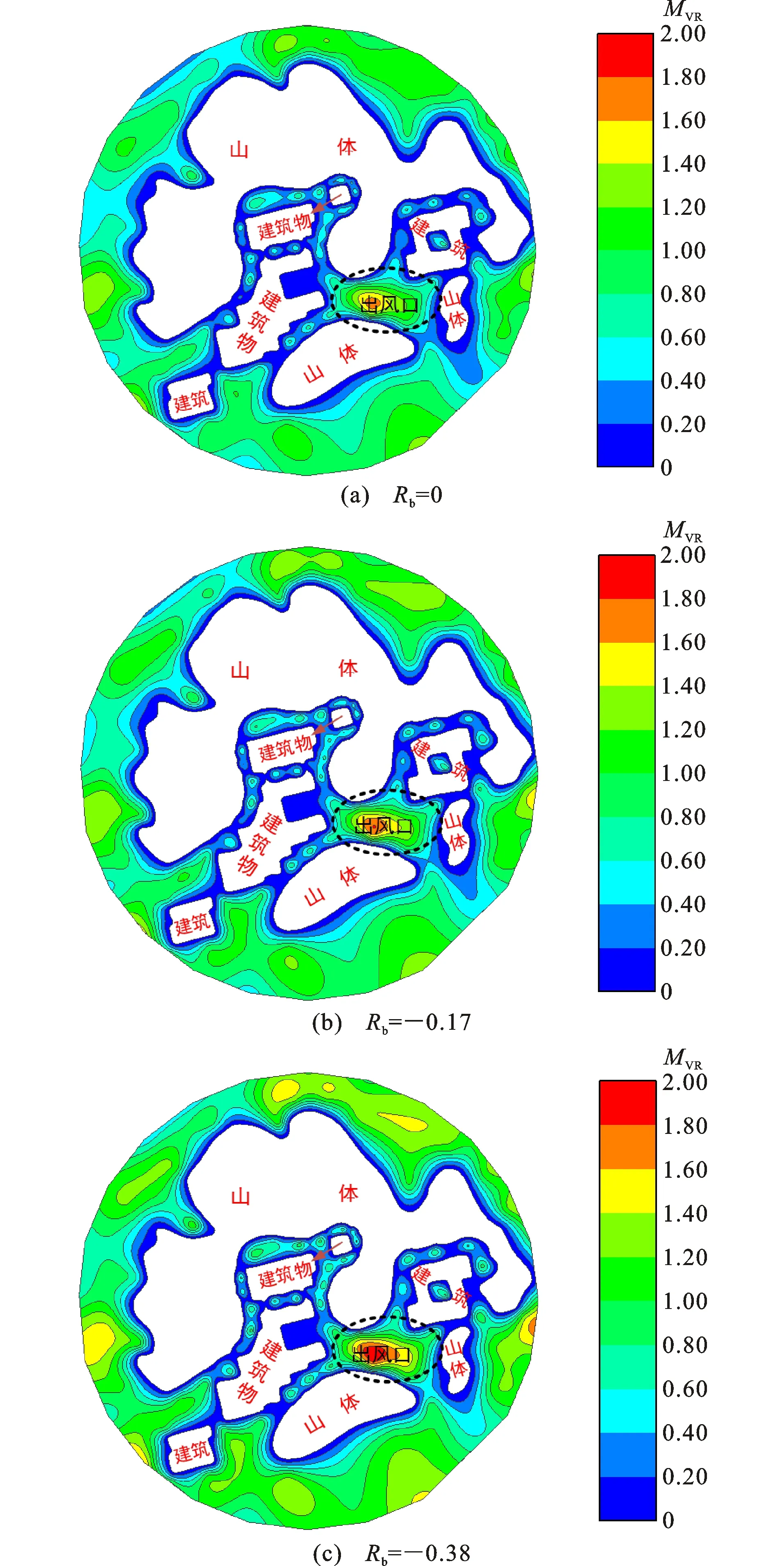
为分析热力效应对小区风环境的影响，对不同工况作用下风环境进行对比分析，如图11所示，其中落在45°线两侧区域测点表示温度对该测点的影响程度大，落在45°线上测点表示温度影响程度较小。从图11发现，在主导风下，风速比在0.6以下的测点受到Rb的影响程度相对较大，风速比在0.6以上温度对风速的影响较小。引入均方根系数，对图11中平均风速进行误差分析，发现均方根系数分别为0.623和0.635，说明两种温度效应对人行高度风环境总体影响较小。

3.2 风剖面

3.3 雷诺应力剖面

3.4 相关性

速度的相关性能够提供与湍流尺度有关的空间信息，并且两点速度的空间相关性已经在既往研究中被广泛讨论[19-21]，对于空间任意一点与参考点的速度相关性可以表示为

(4)

式中：(xref，yref，zref)为参考点的空间坐标；〈·〉为时间平均的过程；σui为速度分量标准差；R(x,y,z)的取值范围为[-1，1]，相关性系数的正负表示两者相关的方向，相关性系数绝对值的大小表示两者相关程度的强弱。

图14为B类地表风下小区整体风速相关性系数云图，以P1点为参考，通过分析发现人行高度相关性系数主要集中在0.2～0.6之间。人行高度相关性系数变化最大点出现在出风口位置，如图14椭圆区域所示，相关性系数最大变化值为0.08。由此可知，温差对人行高度合速度影响较小，可以忽略。值得注意的是，由温差引起的竖直分量对近地面污染物扩散具有重要影响，但当前研究中，由于受测量精度的影响，需结合数值模拟对其展开进一步研究。

3.5 热力效应对风环境舒适度影响分析

目前，对建筑风环境的评价方法主要是超越概率评估法[22]，采用超越阈值概率方法对小区风环境评估时，需要知道建筑周边的流场分布和当地常年的风向风速的概率分布函数。采用Weibull双参数分布确定各风向角下的风速，超越概率计算表达式为

(5)

式中：Pθi为θi风向风速超过风速阈值uTHR的超越概率；Aθi为发生频率；Cθi为尺度参数；Kθi为形状参数。

通过分析常年逐时风速风向统计资料，得到长沙市区8个风向角作用下的Weibull分布参数，如表1所示。表2为小区典型测点的超越概率值汇总表。

基于上述理论对小区测点进行了超越概率分析，得到各测点全风向下行人舒适度风速超越概率。在小区周围建立了110个监测点[图3(b)]，得到小区核心区域测点的行人高度风环境评估结果，如图15所示。从图15可以发现：随着Rb升高，绝大部分测点超越概率适当增加，但其幅度非常小，最大值出现在14号点；随着温度的升高，其风速超越概率值增长3.87%。因此在实践过程中，由温度引起的单纯风环境舒适度变化非常小，可以忽略其影响。

4 结语

(1)通过对不同热力条件下空风洞流场进行分析发现，在-0.38

(2)实际建筑小区人行高度风环境受温度影响整体较小，风速比在0.6以下时测点风速受热力效应影响较大，但风速比在0.6以上时测点温度对风速影响效果相对较小。

(3)热力效应对人行高度风场的相关性与舒适度影响较小，其最大值分别为8%和3.87%，实践过程中可忽略其影响。

(4)试验过程中，由于风速相对较小，所采用的Croba探头很难精确捕捉风场的展向和竖直方向分量信息，同时，人行高度风场分析过程中采用的欧文探头也无法获取风速的不同分量，使得文中结论仅揭示了热力效应对合速度的影响。风场竖向分量对污染物扩散具有重要作用，在后续研究中，需通过数值模拟技术进一步详细研究温度对风场各分量(尤其是竖直分量)的影响。

表1 气象观测资料统计Table 1 Statistics of meteorological data

表2 小区典型测点的超越概率Table 2 Exceedance probability of typical monitoring points in community