起爆方式对间隔装药应力场分布及裂纹扩展的影响
杨仁树,赵 勇,方士正,赵 杰,王 渝,刘 朕
1) 北京科技大学土木与资源工程学院,北京 100083 2) 北京科技大学城市地下空间工程北京市重点实验室,北京 100083 3) 中国矿业大学(北京)力学与建筑工程学院,北京 100083 4) 天津宏泰华凯科技有限公司,天津 301913
柱状药包爆破在工程实践中扮演着重要角色,其激发的应力场更是影响爆破效果的关键因素.针对柱状药包爆破作用机理,学者们分别基于理论分析、数值模拟和模型试验等手段开展了大量研究.近年来,随着数码电子雷管的应用,为精确延时控制的实现提供了可能[1-3].起爆方式(包括起爆点个数[4-6]和起爆点位置[7-8])对爆破效果的影响也越来越被重视.冷振东等[9]通过采用理论分析并结合数值模拟,对比分析了不同起爆方式下被爆介质中的张拉破坏区和压剪破坏区,结果指出在实际爆破工程中可以通过改变起爆点个数来调整爆炸能量的空间分布.高启栋等[10-11]基于理论计算、模型实验、数值模拟的角度分析起爆位置对柱状药包爆轰产物和爆炸能量的分配及其爆炸应力场分布的作用机理,并结合现场试验开展了不同起爆方式下的爆破振动场监测.Onederra等[12]通过建立复合应力爆破模型(HSBM),结合模型实验结果表明:采用孔底起爆时孔底破坏范围显著小于孔口.朱强等[13]为了研究空气间隔装药预裂爆破孔壁岩体损伤分布特征,采用数值模拟结合现场声波测试的手段,表明反向起爆可以减小炮孔底部岩体的最大损伤深度和损伤体积.曲艳东等[14]采用数值模拟研究了间隔装药爆破时不同孔壁介质的扩孔特征、应力场、速度场和能量分布及传播衰减规律,同时分析了不同起爆方式对孔壁介质中冲击波传播规律的影响.
柱状药包在实际爆破过程中,当起爆点处起爆后,基于Starfield迭加法,将柱状药包等效为多个等效半径的单元球形药包,爆轰波沿炮孔轴向传播的过程即是球形药包的逐个起爆过程[15-16].由于爆轰波的传播速度与大部分岩石材料波速在一个量级上,因此爆轰过程存在明显时间效应[7],对应力场分布特征具有重要影响.同时,当采用孔内多点起爆时,由于爆轰波传播的时间效应导致爆轰波、冲击波碰撞叠加的复杂性.因此充分认识柱状药包爆破作用机理对于指导实际生产具有重要意义.
空气间隔装药作为柱状药包爆破时常采用的装药结构[17-22],每一节装药段均布置有单独起爆药包,当每节装药段炸药起爆后,综合考虑碰撞叠加效应及时间效应,装药段起爆点相对位置对空气间隔装药结构下应力场的分布具有重要影响.因此,本文开展了不同起爆点位置对空气间隔装药应力应变场分布影响的模型试验及数值模拟研究.同时,采用透射式焦散线实验系统研究了不同起爆方式对空气段预制裂纹扩展规律的影响.
1 炮孔壁处损伤分布及应变场演化规律
1.1 实验手段
1.1.1 模型试验方案设计
相关研究已经表明,在动荷载作用下有机玻璃板(PMMA)具有与岩石材料相似的动态断裂特性,同时由于PMMA良好的均质性,本次模型试验采用PMMA作为实验材料[23-25],其动态力学参数见表1.模型尺寸为长400 mm、宽300 mm、厚度5 mm,中间布置长60 mm、宽2.5 mm的柱状炮孔,炸药采用叠氮化铅(表2为该炸药爆轰参数).采用径向耦合、轴向不耦合装药,将柱状药包分为两段,上段为装药段(25 mm),装药量控制在45 mg,中间布置空气段(10 mm),下段为装药段(25 mm),装药量控制在45 mg.采用端部起爆(图1中红点所示),两装药段为同时起爆,通过改变装药段起爆点位置,设置三组实验,每组3个试件:(1)两起爆点均布置在靠近空气段一侧为内侧起爆,记为试件 I-n(n=1~3);(2)两起爆点均布置在远离空气段一侧为外侧起爆,记为试件 O-n(n=1~3);(3)两起爆点分别布置在靠近空气段一侧和远离空气段一侧为异侧起爆,记为试件D-n(n=1~3).同时,在空气段中心右侧20 mm处预制一条10 mm长预制裂纹,目的是为了研究不同起爆方式对空气段预制裂纹的动态断裂影响.

图1 模型方案示意图.(a)内侧起爆试件;(b)外侧起爆试件;(c)异侧起爆试件Fig.1 Schematic diagram of the model scheme: (a) inner detonation specimen; (b) outer detonation specimen; (c) antarafacial detonation specimen

表1 PMMA试件动态力学参数表Table 1 Dynamic mechanical parameters of the PMMA specimens

表2 叠氮化铅爆轰参数表Table 2 Relevant detonation parameters of lead(II) azide
1.1.2 数值模拟设计
采用有限元数值模拟软件LS-DYNA按照1:1比例还原模型试验.数值模拟由炸药、空气、有机玻璃三部分组成.由于模拟爆炸问题时存在大变形、大位移等,为了避免网格畸变导致无法计算,在本问题研究中选用任意拉格朗日-欧拉算法,炸药、空气采用欧拉算法,选用关键字*MAT_HIGH_EXPLOSIVE_BURN模拟炸药,关键字*MAT_NULL模拟空气.由于110号材料在模拟陶瓷、玻璃等脆性材料方面的特有优势[26-27],本文采用关键字*MAT_JOHNSON_HOLMQUIST_CERAMICS模拟PMMA,有机玻璃采用拉格朗日算法,采用流固耦合方法计算流体与固体间耦合作用.在*MAT_JOHNSON_HOLMQUIST_CERAMICS材料模型中,D代表累积损伤,主要是基于计算周期内塑性应变的累积增加造成.

式中: Δ εp为加载过程中的累积塑性应变,为压力P下断裂时的塑性应变.
模型建立、网格划分、算法定义、边界条件设置等均采用HYPERMESH前处理软件,如图2所示,以外侧起爆为例,网格采用四边形Quads和三角形Trias划分出面单元,然后沿模型厚度方向划分形成体单元,单元尺寸大小为0.5 mm.根据坐标位置,通过*INITIAL_DETONATION设置不同起爆点.
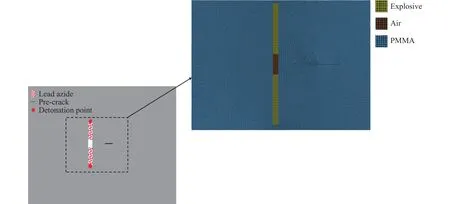
图2 外侧起爆模型示意图及网格划分Fig.2 Schematic diagram and mesh generation of the outer initiation model
1.1.3 超高速数字图像相关实验系统
数字图像相关方法(Digital image correlation,DIC,又称数字散斑相关法)作为研究介质全场应变场的光学测试方法,近年来,随着高速摄像技术的迅猛发展,DIC已被广泛应用于爆炸及冲击动力学等实验研究[28-29].由于聚碳酸酯板相对均质且受小药量药包爆破时不会产生爆生裂纹,因此选取聚碳酸酯板为实验材料,炸药采用叠氮化铅,聚碳酸酯板长×宽×厚=300 mm×300 mm×5 mm,试件中心位置设置长×宽×厚=60 mm×2 mm×2.5 mm的柱状炮孔.同时为最大限度避免人为因素带来的误差,表面散斑采用打印技术将制作好的散斑图像印于试件表面.
如图3所示,适用于爆炸荷载作用下的超高速数字图像相关系统采用高速拍摄系统、照明系统、同步控制及起爆系统搭建.

图3 超高速数字图像相关实验系统Fig.3 Experimental setup of the high-speed digital image correlation
(1)高速拍摄系统:相机型号为Kirana-5M型,拍摄图像分辨率固定为924像素×768像素,单次拍摄采集次数为180次.本次实验设定拍摄频率为160万帧,即相邻两张照片间的时间间隔为0.625 μs.
(2)照明系统:由FH-500型氙气闪光灯和同步控制器组成,单次恒定光强照明时间可以达到2 ms,同时可以实现曝光时间的同步控制.
(3)同步控制及起爆系统:采用多路时序触发系统与同步控制仪,可以精确控制起爆时间,同时施加同步信号给高速相机和照明系统,保证信息的同步捕捉.
(4)后处理系统:采用VIC-2D软件,对采集的照片通过标准化的平方差相关函数进行数字图像相关计算.
具体实施步骤:通过同步控制及起爆系统首先给氙气闪光灯照明信号,当达到稳定光源后,同时给试件起爆信号和高速相机拍摄信号,通过电脑将高速相机拍摄到的照片记录用于后处理系统分析.
1.2 炮孔壁处损伤分布规律
采用多路时序触发系统结合同步控制仪引爆炸药后,试件爆后形态如图4所示.可以看出:不同起爆方式下炮孔壁处呈现了不同破坏形态,但在装药段两侧均出现明显粉碎区和裂隙区.

图4 试件破坏形态与裂纹分布.(a)试件 I-1;(b)试件 O-1;(c)试件 D-1Fig.4 Fracture patterns and crack distributions of the specimens: (a) specimen I-1; (b) specimen O-1; (c) specimen D-1
采用分形几何评价孔壁处宏观损伤破坏情况.自谢和平[30]首次将几何分形运用于岩石的破碎、损伤和断裂等问题后,诸多学者[31-32]将其作为研究介质破坏问题的一种手段.在分形几何理论中,计盒维数Dn是一个能够反映损伤严重程度的稳定指数,其具体算法如下:
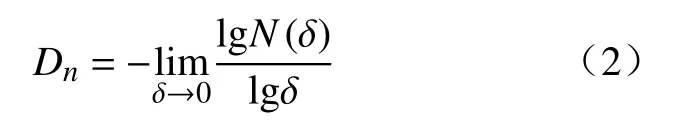
式中:N(δ)为覆盖δ边长盒子个数,δ为计盒尺寸.
评价材料的破坏情况时常采用损伤度w进行定义.本节所研究的损伤为材料受荷载作用后的宏观表象,通过建立计盒维数Dn与损伤度w之间关系[31-32]:

式中:Dn表示介质损伤区域的分形维数;D0表示爆炸前介质中初始损伤区域的分形维数,在这里D0=0;本次研究主要针对二维平面模型,在此Dmax=2.
采用整像素分析方法,沿炮孔轴向方向自上至下以两倍炮孔直径为梯度进行划分,炮孔壁处宏观损伤情况进行二值化处理,每张图片大小均为310像素×25像素,计盒维数计算过程中网格的最小划分单位是一个像素.图5所示为进行计盒维数计算后拟合得到的直线,由于篇幅所限,文中仅列出部分实验条件下计盒维数拟合曲线.可以看出:介质损伤情况很好地符合分形破坏规律.
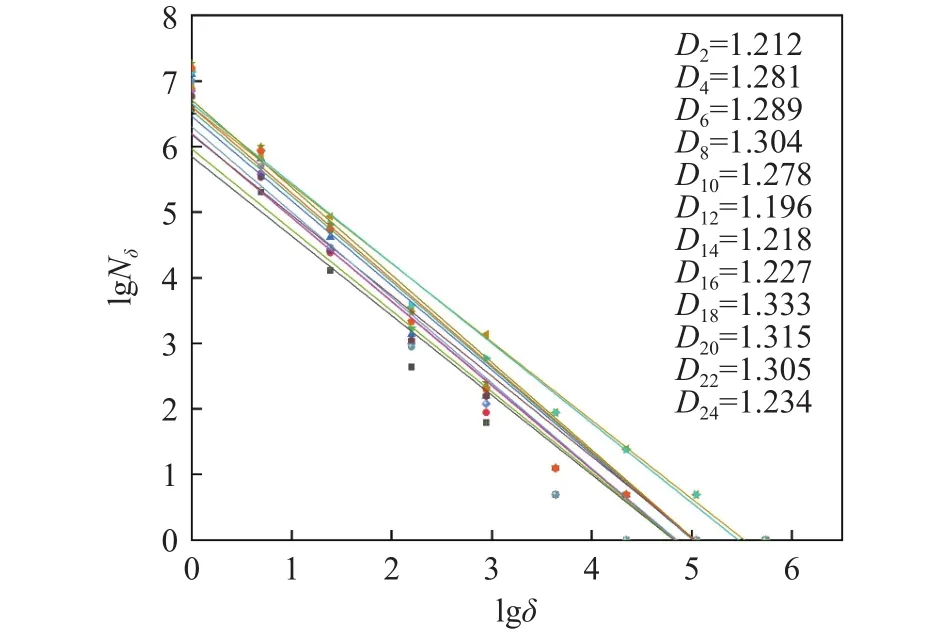
图5 裂纹轨迹的计盒维数拟合曲线Fig.5 Fitting curve of the box-counting dimension of the crack trajectory
图6显示了沿炮孔轴向自上至下炮孔壁损伤度变化情况.可以看出:装药段在不同起爆方式下各起爆点位置对应的损伤度最小,沿传爆方向损伤度逐渐增大,很好地印证了柱状药包爆炸时的时间效应和能量累积效应.值得注意的是,柱状药包起爆后冲击波传播过程是能量积聚速率变化的过程.沿传爆方向,通过孔壁处损伤度在初始阶段迅速增大可以看出能量积聚速率在初始阶段较快,随后能量积聚速率逐渐减缓.同时由于本次模型试验是一个二维平面问题,随着冲击波传播至接近非起爆端时,当非起爆端为炮孔两端,从炮孔端部产生裂纹可以看出,由于端部应力集中,部分能量沿炮孔端部释放;当非起爆端为空气段,部分能量透过空气释放.因此远离起爆端时损伤度又会有所减小.当采用外侧起爆时,垂直于空气段中心两侧均产生损伤,而采用其他起爆方式时,空气段均未出现损伤.这主要是由于相向而行的冲击波在空气段中心处发生碰撞叠加导致应力骤然增大,入射至炮孔壁后产生粉碎区,随后冲击波转变为应力波,以拉剪破坏的形式产生裂隙,爆生气体的“气楔”作用导致径向裂纹扩展.外侧起爆时无论是空气段孔壁处还是预制裂纹尖端均形成了“分叉型”裂纹,这主要是由于材料的自身性质决定,其次应力波叠加产生的高应力作用是形成这种裂纹的必要条件.
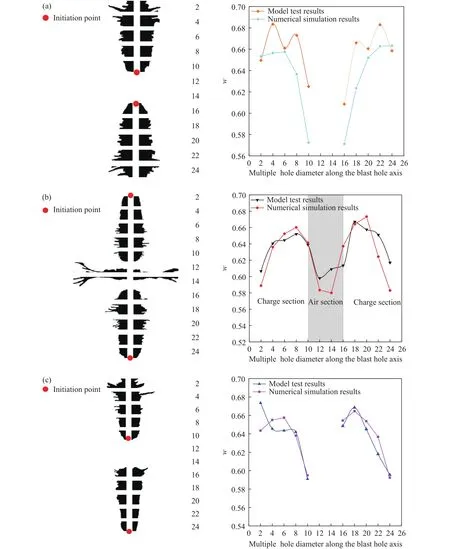
图6 炮孔孔壁处损伤二值图及损伤分布.(a)内侧起爆;(b)外侧起爆;(c)异侧起爆Fig.6 Binary diagram of the damage at the hole wall and the damage distribution law of the blasthole axial hole wall: (a) inner detonation; (b) outer detonation; (c) antarafacial detonation
采用数值模拟计算后得到炮孔周围介质的破坏情况,图7中红色区域代表粉碎区,绿色区域代表裂隙区,结果如图7所示,分别对不同起爆方式下破坏结果进行二值化处理,选取和模型试验同样梯度由上至下进行划分,基于分形维数进行损伤度计算,可以看出:两者从数值和变化趋势上保持了较好的一致性,数值模拟高度还原了模型实验结果.
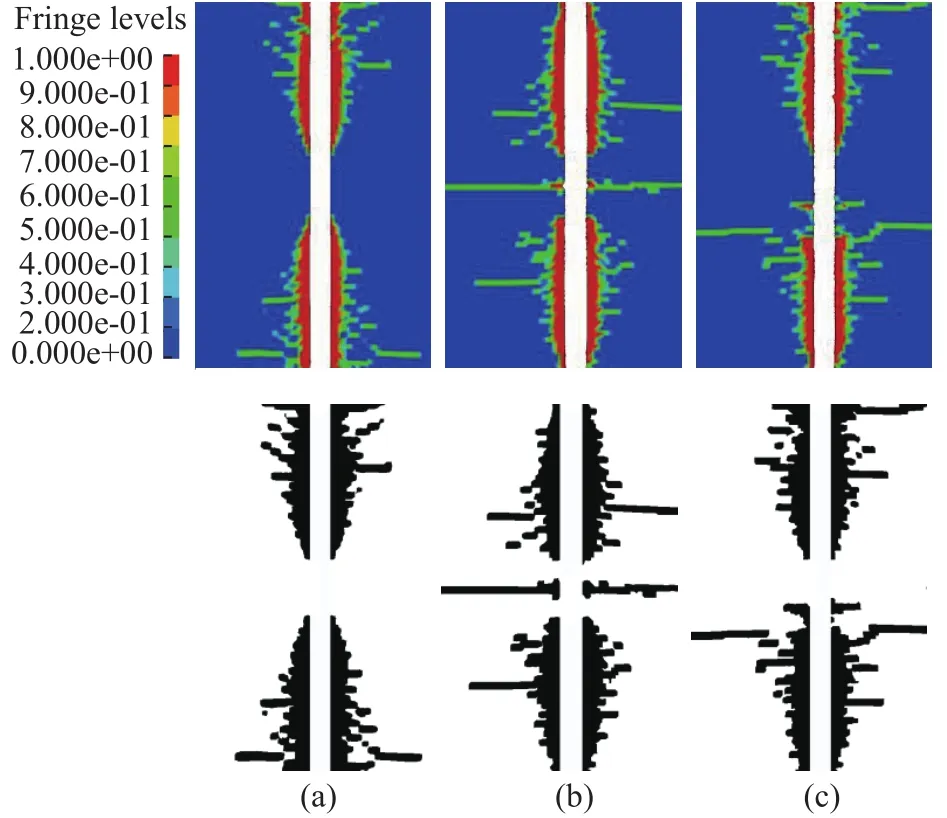
图7 基于数值模拟下炮孔孔壁损伤分布示意图.(a)内侧起爆;(b)外侧起爆;(c)异侧起爆Fig.7 Schematic diagram of the blasthole axial wall damage distribution based on numerical simulation: (a) inner detonation; (b) outer detonation; (c) antarafacial detonation
1.3 空气间隔装药应变场、应力场分布规律
三种起爆方式下轴向应变云图和径向应变云图表现出一定程度相似性,这可能是由于装药段长度的限制导致爆轰波传播过程的时间效应不明显,从应变场的角度未能将三者区分.因此,文中仅列出内侧起爆时应变场演化过程,如图8所示,云图中蓝紫色区域为受压应变区,红橙色区域为受拉应变区.以炸药起爆时刻为零时刻,起爆后,如图8(a)所示径向应变场,在t=21.875 μs时,受爆炸强冲击波作用,在整个炮孔两侧表现出明显“半椭圆状”的压应变区.随后在t=46.25 μs时,压应变区明显增大,呈“葫芦状”继续扩展,同时,在炮孔端部四个位置出现明显的拉伸应变区.在t=65 μs时,压应变区产生分离,左右两侧均产生两个主压应变区,分别呈“月牙状”和“葫芦状”继续扩展.在t=82.5 μs时,靠近炮孔主压应变区继续分离,左右两侧形成三个明显主压应变区.图8(b)所示为轴向应变场,t=46.25 μs时起爆后在炮孔左右两侧率先产生主拉伸应变区,炮孔端部形成半环向压缩应变区,随着爆炸应力波的传播,主拉伸应变区及主压缩应变区向外扩展的过程中逐渐削弱.
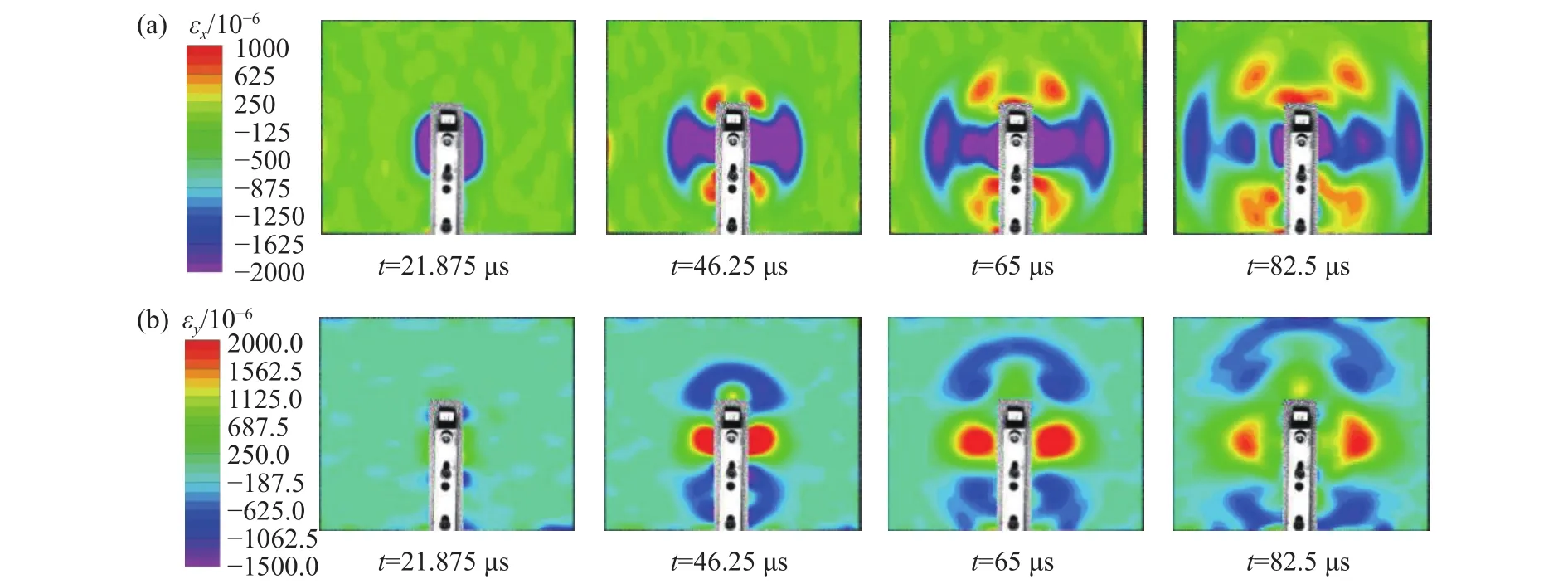
图8 爆炸应变场演化过程.(a)应变分量 εx 的演化过程;(b)应变分量 εy 的演化过程Fig.8 Evolution process of the blasting strain field: (a) evolution of strain component εx; (b) evolution of strain component εy
为了定量分析不同起爆方式下空气段应变场变化规律,如图9所示,选取距空气段中心位置间距分别为25、35、45、…75、85 mm总计7个测点,测点编号分别为A1、A2、…A6、A7.
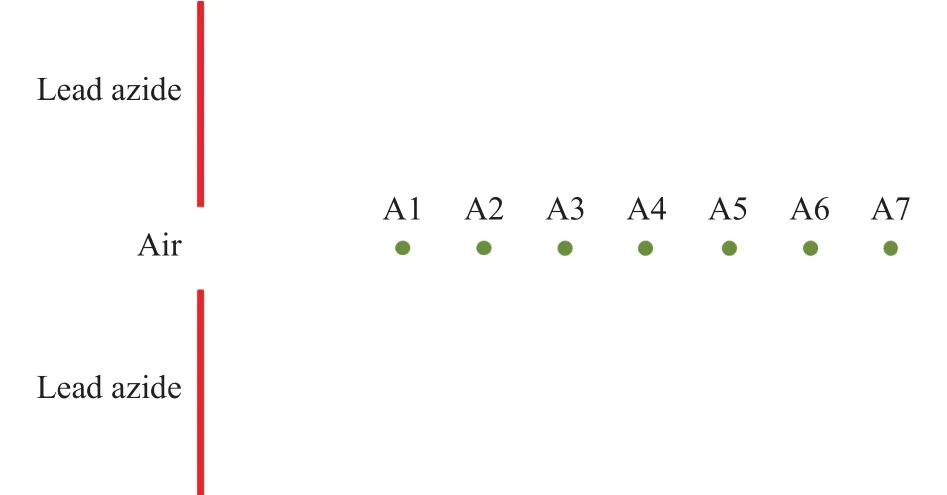
图9 测点位置示意图Fig.9 Diagram of the gaging point position
如图10所示,分别提取七个测点径向应变和轴向应变,进行平滑处理后得到各测点应变时程曲线.可以看出:不同起爆方式下径向应变主要表现为压应变,测点距离空气段中心位置较近时均表现为双峰值的分布特点,这是由于柱状药包起爆后,两装药段炮孔在应力波传播过程中不断叠加的结果.不同的是,采用内侧起爆、异侧起爆时,两个峰值较为接近;外侧起爆时,以测点A1、A2为例,第二个峰值显著大于初始峰值,A1初始峰值为 4541×10-6,第二个峰值为 5849×10-6,是初始峰值的1.29倍,A2初始峰值为2972×10-6,第二个峰值为3603 ×10-6,是初始峰值的1.21倍.这主要是由于柱状药包非起爆端应变大于起爆端应变的特点,当外侧起爆时空气段位于柱状药包非起爆端,应变场产生高强度叠加,因此外侧起爆时A1、A2测点第二个峰值较大.外侧起爆时A1~A7测点压应变峰值分别为内侧起爆时的1.31、1.08、0.79、0.77、0.81、0.82、0.84倍,异侧起爆时A1~A7测点压应变峰值分别为内侧起爆时的1.11、1.14、1.02、1.00、0.99、0.95、0.98倍.在炮孔近区,外侧起爆时压应变显著大于内侧起爆,在炮孔远区,外侧起爆时压应变小于内侧起爆,表明外侧起爆时空气段应变场具有强衰减的特征.对于异侧起爆,各测点应变值与内侧差别较小,这两种起爆方式下应变场强度具有一定程度的相似性.
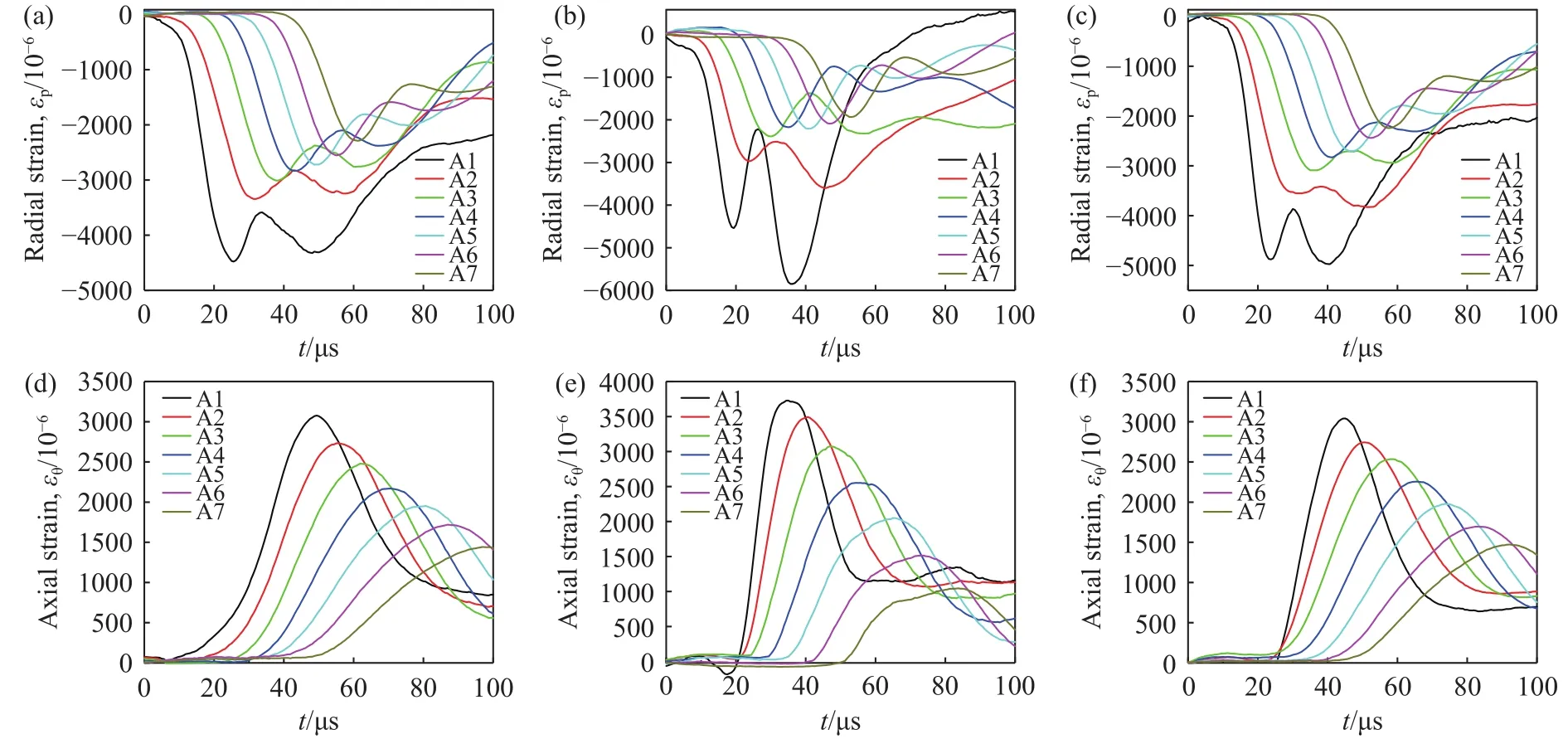
图10 应变时程曲线.(a)内侧起爆径向应变;(b)外侧起爆径向应变;(c)异侧起爆径向应变;(d)内侧起爆轴向应变;(e)外侧起爆轴向应变;(f)异侧起爆轴向应变Fig.10 Strain-time curves: (a) radial strain of inner initiation; (b) radial strain of outer detonation; (c) radial strain of antarafacial detonation; (d) axial strain of inner initiation; (e) axial strain of outer detonation; (f) axial strain of antarafacial detonation
各起爆方式下轴向应变主要表现为拉应变,测点的应变变化特征相似,均表现出达到峰值后逐渐衰减的特点.不同的是,各起爆方式下轴向应变场呈现时效差异性,以A1测点为例,当内侧起爆时,5.625 μs时产生初始拉应变,43.75 μs后达到峰值,外侧起爆、异侧起爆时,上升段持续时间呈现短时的特性,分别于 23.12 μs、20 μs后急速达到峰值,下降段持续时间三者差别较小分别为22.5、15、23.75 μs.
如图11所示,提取各测点的应变峰值进行拟合,得到空气段中心位置应变的衰减规律.内侧起爆、外侧起爆、异侧起爆时径向应变衰减指数分别为0.515、1.056和0.657,轴向应变衰减指数分别为0.542、0.759和0.524.可以发现,不论是径向应变还是轴向应变,外侧起爆时应变场的衰减系数最大,对于径向应变,异侧起爆衰减系数大于内侧起爆,对于轴向应变,异侧起爆和内侧起爆则相差较小.
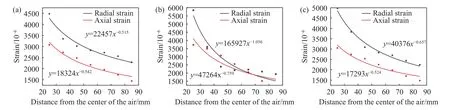
图11 应变峰值及其衰减拟合曲线.(a)内侧起爆;(b)外侧起爆;(c)异侧起爆Fig.11 Strain peaks and their attenuation-fitting curves: (a) inner detonation; (b) outer detonation; (c) antarafacial detonation
受制于炮孔夹具对相机视场的影响,难以通过数字图像相关方法计算得到炮孔周边应变场演化过程.采用1.1.2数值模拟模型,沿炮孔轴向方向选取炮孔孔壁处总计60个测点,如图12所示,提取各测点单元压力峰值,以炮孔内单个装药段为例,当起爆点起爆后,孔壁处压力峰值迅速增大,随着爆炸应力波的传播,压力值逐渐稳定,距非起爆端一定距离时再次增大至最大值,随后压力值又有所减小.在空气段,内侧起爆时压力值分布呈现山谷状,空气段中心峰值为69.63 MPa,外侧起爆时压力值分布呈现山峰状,空气段中心位置峰值为219.31 MPa,约为内侧起爆时3.15倍,从数值模拟的角度解释了空气段中心位置处发生破坏的现象.异侧起爆时压力值分布呈现斜坡状,空气段中心峰值为103.81 MPa,约为内侧起爆时1.49倍.可以看出不同起爆方式对沿炮孔轴向孔壁处压力分布影响显著,装药段主要体现在压力峰值位置和压力分布形态两个方面,空气段主要体现在压力峰值大小和压力分布形态两个方面.
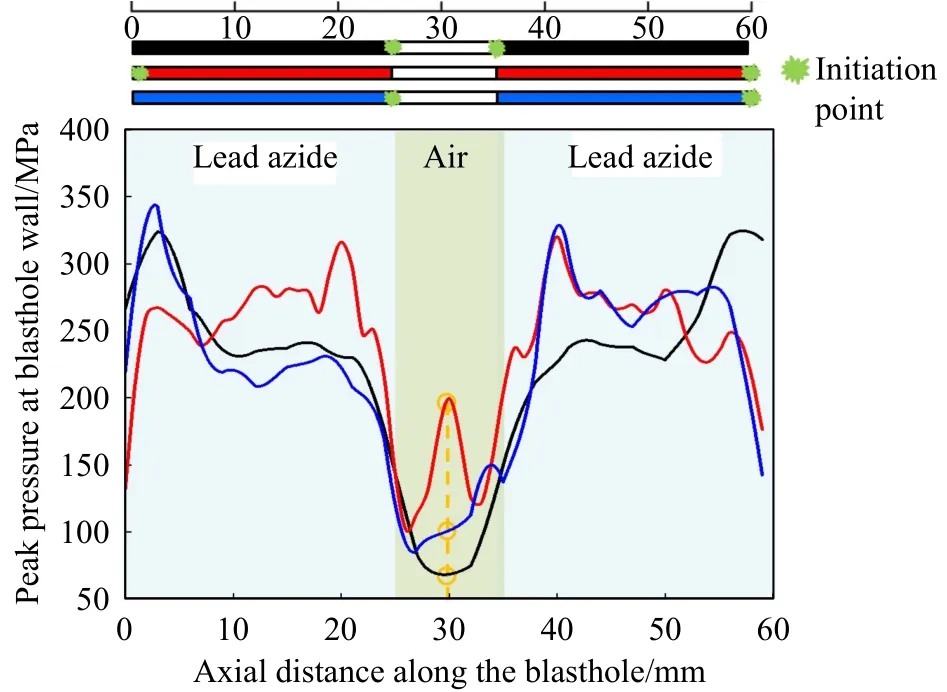
图12 不同起爆方式下孔壁处压力分布情况Fig.12 Pressure distribution at the blasthole wall under different initiation methods
2 不同 起爆方 式下空 气段预 制裂纹 扩展规律
2.1 数字激光动态焦散线实验系统
透射式数字激光动态焦散线实验系统主要用于研究可透射式光学材料的动态断裂特性.平行光穿过透明材料时,由于试件受外荷载(拉、压)作用导致厚度方向发生变化,折射率改变引起光线路径的偏移,导致相机接收面处产生阴影区,该区域即为焦散斑.
图13所示为数字激光动态焦散线实验系统示意图,主要由电脑、高速相机、爆炸加载装置、场镜1、场镜2、扩束镜、激光器组成.高速相机为日本Photron公司生产的Fastcam-SA5(16G)型彩色高速相机,其自带软件可实现对实验图像的采集和处理.激光光源为输出功率为0~300 mW、波长为532 nm的绿光光源,具有光强高、稳定性好的特点,可以保证在极短时间内拍摄到清晰照片.实验过程中设置相机拍摄频率为210000 s-1,相邻两张照片之间的时间间隔为4.76 μs.

图13 数字激光动态焦散线实验系统Fig.13 Experimental setup of the digital laser dynamic caustics
动态应力强度因子(DISF)作为表征裂纹尖端应力场强弱的物理量,通常采用下式计算[23-25]:
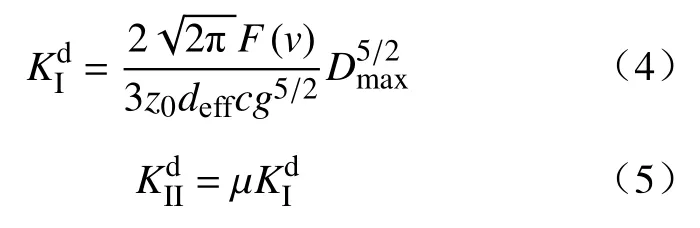
式中:F(v)为速度调节函数,在这里取F(v)≈1;z0为参考平面到试件表面的距离,根据实验情况取z0=800 mm;c为应力光学常数,取c=0.85×10-10m·N-1;deff为试件的有效厚度,在该实验条件下deff=5 mm;g为数值因子,取g=3.17.μ为复合裂纹尖端应力强度因子的比值,采用公式(Dmax-Dmin)/Dmax.Dmax和Dmin通过实际拍摄图片测量后得到.
2.2 预制裂纹断裂行为分析
图4所示(见1.2节)为不同起爆方式下空气段预制裂纹的断裂情况.三种起爆方式下空气段预制裂纹两端均发生起裂产生裂纹,但裂纹起裂夹角与扩展长度有所不同.
定义裂纹远离炮孔方向的扩展长度为l,偏离水平方向的角度为θ.统计用于描述预制裂纹断裂行为的物理量如表3所示.采用外侧起爆时,裂纹呈现水平扩展,平均扩展长度l达到58.7 mm;内侧起爆时,裂纹同样呈现水平扩展,平均扩展长度l达到11 mm,相比裂纹扩展长度减少81.26%;异侧起爆时,裂纹与预制裂纹水平方向呈11°扩展,扩展平均长度l为9.7 mm.可见:不同起爆方式对空气段预制裂纹起裂夹角与扩展长度均有重要影响.
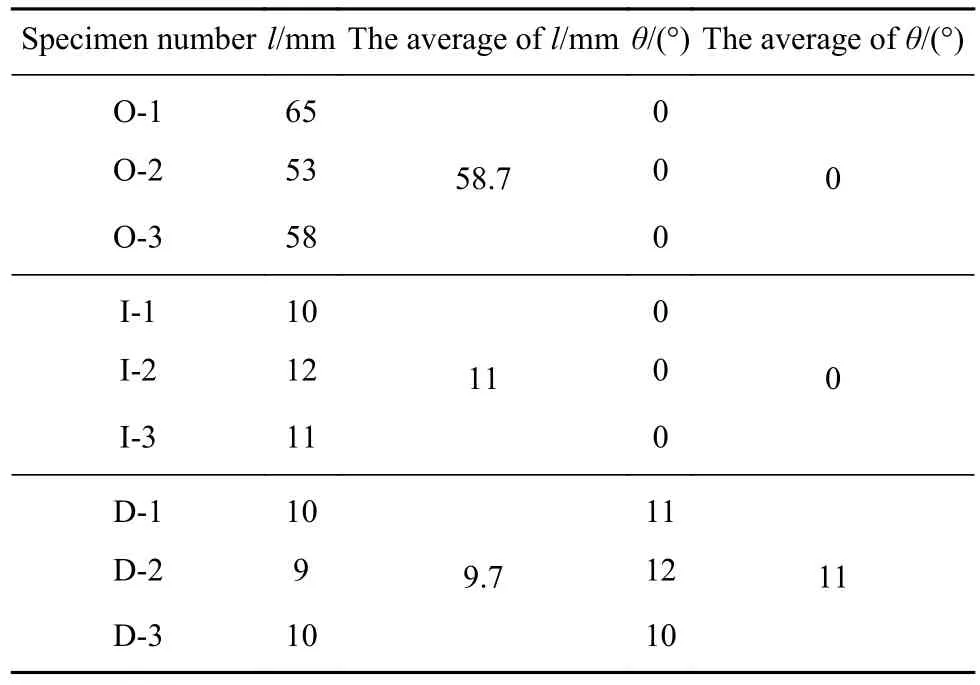
表3 试件断裂情况统计表Table 3 Statistical table of specimen fractures
图14所示为试件断裂过程不同时间段对应的焦散线实况照片,图15所示为各试件动态应力强度因子随时间的变化曲线.对于试件O-1、I-1,由于两起爆点相对于预制裂纹呈对称分布,产生的爆炸应力波同样关于预制裂纹对称,两组应力波到达预制裂纹端部时间一致,预制裂纹端部受两组爆炸应力波作用后,裂纹分别于28.56 μs、19.04 μs时出现焦散斑,焦散斑呈现典型的I型焦散斑,能量迅速汇聚满足起裂所需,DISF峰值分别为 0.97 MN·m-3/2、1.31 MN·m-3/2,由于应力强度因子的大小反映了能量累积的程度,表明试件O-1裂纹端部较容易起裂,试件I-1裂纹端部较难起裂.随后DISF逐渐降低,裂纹止裂.同时观察到试件I-1在119 μs时DISF出现了小幅度增大后又再次降低,裂纹并未继续扩展,DISF峰值为0.52 MN·m-3/2.而试件O-1的DISF出现了两次大幅度增大导致裂纹继续扩展,DISF峰值分别达到0.65 MN·m-3/2、1.02 MN·m-3/2.两种起爆方式下DISF出现反弹现象主要是由于试件的边界效应导致压缩波运动至试件边界后发生反射,反射拉伸波与裂纹端部相互作用导致裂纹继续扩展.由于反射拉伸波强度与压缩波强度大小呈现正相关性,这也从另一个角度反映当外侧起爆时,介质内发生应力叠加导致应力场增强效果显著.

图14 爆生裂纹扩展的焦散线照片.(a) O-1; (b) I-1; (c) D-1Fig.14 Caustics images of the blast-induced crack during propagation: (a) O-1; (b) I-1; (c) D-1
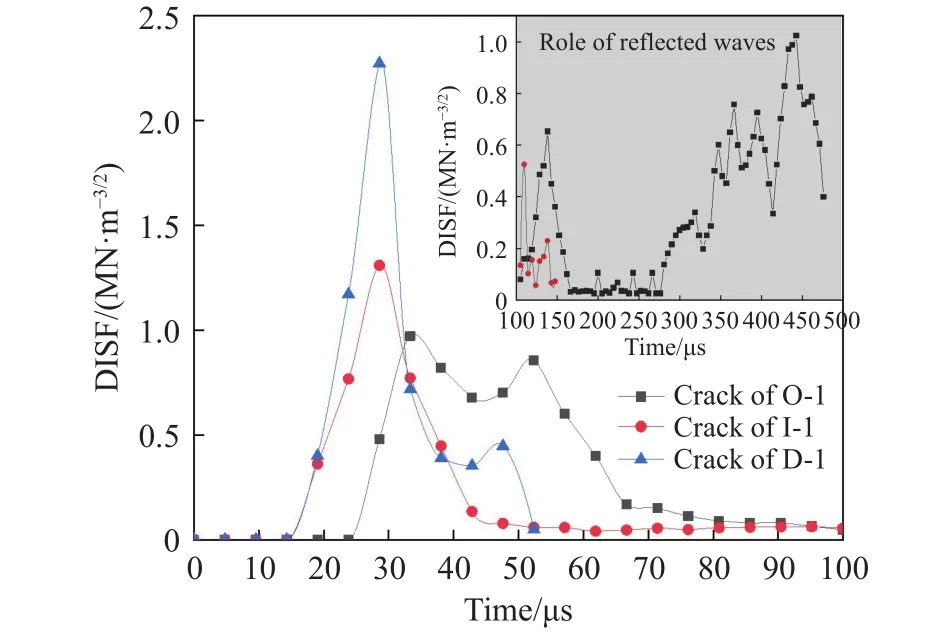
图15 试件裂纹尖端的动态力学参数随时间的变化曲线Fig.15 Dynamic mechanical parameters at the crack tip in the three specimens
试件D-1受应力波作用出现焦散斑后迅速达到裂尖起裂所需能量,DISF峰值为2.3 MN·m-3/2,DISF值为试件O-1的2.37倍,试件I-1的1.76倍,与之前提到的起爆方式相比,说明该起爆方式下裂纹起裂较难.裂纹尖端焦散斑呈现Ⅰ-Ⅱ混合型,这主要是由于两装药段爆炸产生应力波通过预制裂纹尖端时存在路程差,裂纹偏转是两组应力波相互博弈的结果.
对裂纹端部起裂时刻焦散斑放大(图16(a)、(b)、(d)所示),图中黄色线条为通过理论计算后得到的焦散斑轮廓示意图,图16(c)、(e)所示为根据焦散线映射方程计算得到的理论焦散线示意图,图中“*”表示投射到平面出光斑散点分布,空白部分即对应焦散斑,理论与实验结果具有较好的一致性.试件O-1和I-1均为典型的Ⅰ型裂纹,表明裂纹的起裂是由拉伸破坏引起,试件D-1起裂模式呈现Ⅰ-Ⅱ混合型,具体表现为拉-剪破坏,理论与实验结果同样具有较好的一致性.
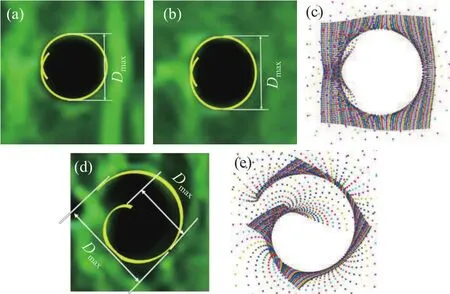
图16 实际焦散斑示意图及理论计算结果.(a)O-1, t=40 μs (Model I);(b) I-1, t=30 μs (Model I );(c)KⅡ/KI=0;(d)D-1, t=30 μs(Model I-II);(e)KⅡ/KI=2.2Fig.16 Practical caustic speckle diagram and theoretical calculation results: (a) O-1, t=40 μs (Model I);(b) I-1, t=30 μs (Model I);(c)KⅡ/KI=0;(d)D-1, t=30 μs(Model I-II);(e)KⅡ/KI=2.2
2.3 基于 LS-DYNA 的裂纹起裂原因探究
如图17所示,绿色代表预制裂纹端部受爆破荷载作用后破坏区域,对比模型实验情况可以看出:内侧起爆和外侧起爆时端部裂纹均呈现直线扩展,后者裂纹较长,异侧起爆时预制裂纹端部偏离水平方向呈现一定角度扩展,数值模拟较好地还原了模型实验结果.

图17 预制裂纹端部裂纹扩展结果Fig.17 Crack propagation results of the precrack tip
如图18所示,选取预制裂纹尖端三个单元(自上至下编号分别为H1223216、H1221214、H1220 017),提取测点最大主应力随时间的变化关系,从微观角度解释端部裂纹起裂原因,如图19所示.可以看出:内侧起爆和异侧起爆时,H1221214对应最大主应力最大,且H1223216和H1220017单元对应主应力时程变化基本保持一致,因此裂纹沿水平方向扩展,而内侧起爆时该单元最大主应力194 MPa远远大于外侧起爆时的119 MPa,表明内侧起爆时裂纹起裂韧度较大,裂纹扩展能力较差.当异侧起爆时,图20所示,H1221214对应最大主应力最大,裂纹向右扩展,但H1223216主应力大于H1220017且持续时间较长,裂纹有向上偏转的趋势,这主要是由于两装药段起爆后应力波扩展至该位置时存在路程差,以预制裂纹为轴应力波呈现非对称传播,率先到达的应力波发生绕射后作用于裂纹尖端两侧单元,随后到达的应力波继续作用于单元,单元受非对称力作用.沿裂纹扩展方向依次取6个单元(自上而下、从左到右取两列单元,编号分别为H1226387、H1224476、H1222614和 H1229166、H1227080、H1225015),如图20所示,第二列仍然是水平方向对应单元H1224476最大,H1226387主应力大于H1222614,第三列时靠近上端单元H1229166对应主应力最大,裂纹发生偏转.造成数值模拟与模型实验结果呈现一定差异的原因可能是由于数值模拟网格尺寸大小的影响,导致裂纹端部起偏滞后.

图18 预制裂纹端部单元Fig.18 Precrack tip element
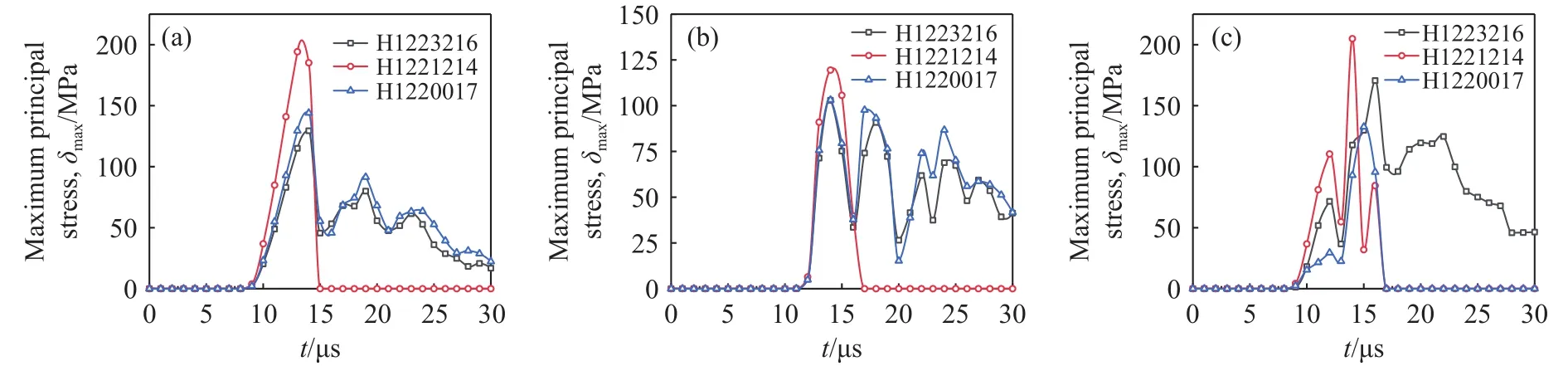
图19 图18所示单元最大主应力随时间的变化关系.(a)内侧起爆; (b)外侧起爆; (c)异侧起爆Fig.19 Relationship between maximum principal stress and time of element in Fig.18: (a) inner detonation; (b) outer detonation; (c) antarafacial detonation
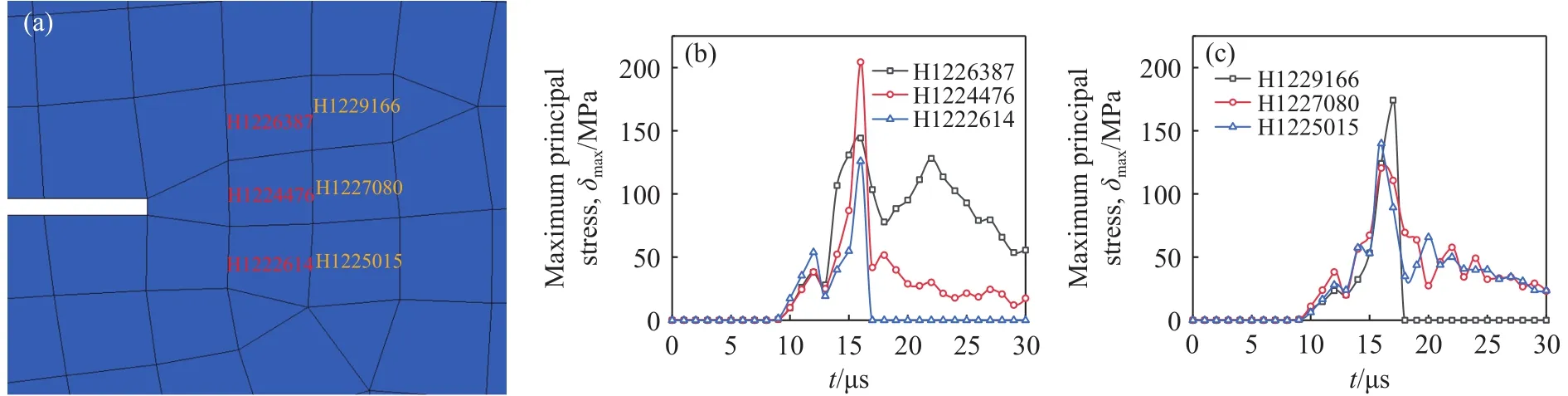
图20 异侧起爆时单元最大主应力随时间的变化关系.(a)选取单元示意图; (b)单元H1226387、H1224476、H1222614; (c)单元H1229166、H1227080、H1225015Fig.20 Relationship between maximum principal stress and time of the unit under antarafacial-initiation: (a) schematic diagram of selected elements;(b) element H1226387, H1224476 and H1222614; (c) element H1229166, H1227080, H1225015
3 结论
(1)柱状药包炮孔两侧产生的损伤范围具有显著的分形特征.装药段各起爆点位置对应的损伤度最小,沿传爆方向损伤度逐渐增大,至非起爆端时由于能量积聚速率减小及部分能量耗散,损伤度又会有所减小.当采用外侧起爆时,垂直于空气段中心两侧均产生损伤,而采用其他起爆方式时,空气段均未出现损伤.
(2)基于数值模拟,研究了炮孔孔壁处压力峰值分布情况,不同起爆方式对沿炮孔轴向孔壁处压力分布影响显著,装药段主要体现在压力峰值位置和压力分布形态两个方面,空气段主要体现在压力峰值大小和压力分布形态两个方面.
(3)不同起爆方式下预制裂纹端部断裂行为差别较大.采用内侧起爆、外侧起爆时,裂纹均为水平扩展,呈现典型Ⅰ型裂纹,裂纹起裂主要由拉伸破坏引起,异侧起爆时裂纹起裂为Ⅰ-Ⅱ混合型,具体表现为拉-剪破坏,裂纹与水平方向呈11°夹角扩展.基于最大主应力破坏准则,从数值模拟的角度解释了裂纹断裂行为差异的现象.
(4)不同起爆方式对空气段应变场径向压应变的影响主要体现在应变大小、衰减速度两个方面,采用外侧起爆时,压应变具体表现为高强度、快衰减的变化特征,异侧起爆次之,内侧起爆压应变强度最低,衰减最慢.对轴向拉应变的影响主要体现在时效性、衰减速度两个方面,采用外侧起爆、异侧起爆时,拉应变极短时间内迅速达到拉应变峰值,内侧起爆时则相对较慢;外侧起爆时衰减系数最大,异侧起爆和内侧起爆衰减系数相差较小.

