基于DE算法和NURBS曲线的ICP-AES光谱基线校正方法研究
廉小亲,陈彦铭,王宇乔,刘 钰
1.北京工商大学人工智能学院,北京 100048 2.北京工商大学中国轻工业工业互联网与大数据重点实验室,北京 100048
引 言
电感耦合等离子体原子发射光谱法(inductively coupled plasma atomic emission spectrometry,ICP-AES)是一种以电感耦合等离子体为激发光源的原子发射光谱分析技术,具有多元素同时检测、分析速度快以及准确度高等特点,被广泛应用于稀土、冶金、化工、无机材料和医学等众多领域[1-2]。然而在ICP-AES测量过程中,受仪器暗电流和光源杂散光的影响,测量所得的光谱通常存在一定程度的基线漂移现象,造成元素含量定量分析误差,因此在测量过程中往往需要对光谱进行基线校正处理[3-4]。
目前较为常见的基线校正方法包括迭代多项式拟合法[5-6]、导数法[7-8]、移动窗口平滑法[9-10]、小波变换法[11]、分段多项式拟合法和分段样条拟合法[12-14]等。迭代多项式拟合法的实现步骤较为简单,但是对于不同的光谱信号,多项式拟合阶数往往需要论证确定,难以建立一种通用性较强的光谱基线拟合模型。导数法和移动窗口平滑法实现原理同样相对简单,但二者均会在时域内降低光谱的分辨率,影响光谱的峰形,不利于后期的定量分析。小波变换也能够有效去除光谱基线,但需要针对不同的光谱信号建立相应的小波基函数,因此算法的运算量相对较高,应用效率也相对较低。分段多项式拟合法在一定程度上克服了迭代多项式拟合法中阶数难以确定的问题,但是相比于分段样条拟合法,分段多项式拟合法有时无法保证全波段范围下的拟合误差,临界处拟合基线的平滑性也较差。样条拟合法根据内接点的分布方式可分为均匀样条拟合和非均匀样条拟合,均匀样条拟合由于内接点的分布缺乏目的性,当光谱基线漂移较为剧烈时,最终的拟合效果和校正效果较为一般;而非均匀样条拟合则弥补了均匀样条拟合的不足之处,能够拟合出更为理想的光谱基线,但非均匀样条拟合过程中通常需要针对不同的光谱基线选定合适的内接点序列和控制点序列,因此会引入大量的人力成本,且难以保证每次选取的内接点序列和控制点序列较为适合。
针对以上问题,本文提出一种基于差分进化算法(differential evolution,DE)和非均匀B样条(non uniform rational B-spline,NURBS)曲线模型的ICP-AES光谱基线校正方法,通过对比光谱信号基线校正前和校正后的特征分布情况,基于NURBS曲线模型建立光谱基线校正评价函数,并利用差分进化算法进行求解,最终拟合出相应的光谱基线;该方法不仅能够充分发挥非均匀B样条曲线在光谱基线拟合问题上的优势,也能够利用差分进化算法全局寻优的特点自行计算出合适的内接点序列和控制点序列,有效地克服了非均匀B样条曲线拟合过程中内接点序列和控制点序列选取困难的问题,同时也能够获得更好的基线校正效果。
1 实验部分
1.1 ICP-AES光谱基线校正原理
本文提出的基于差分进化算法和非均匀B样条曲线的ICP-AES光谱基线校正方法流程如图1所示。原始光谱数据首先通过高斯滤波消除部分高频噪声信号,其次筛选光谱信号中的极小值点,以极小值点集合的相对标准偏差为度量准则、以NURBS曲线模型的控制点序列和内接点序列为寻优参数,建立光谱基线校正评价函数,然后利用差分进化算法求解该评价函数的最优解,即使得极小值点集合相对标准偏差最小时的控制点序列和内接点序列,最后,通过NURBS曲线模型拟合该控制点序列和内接点序列对应的曲线作为光谱基线,以此实现光谱基线校正。
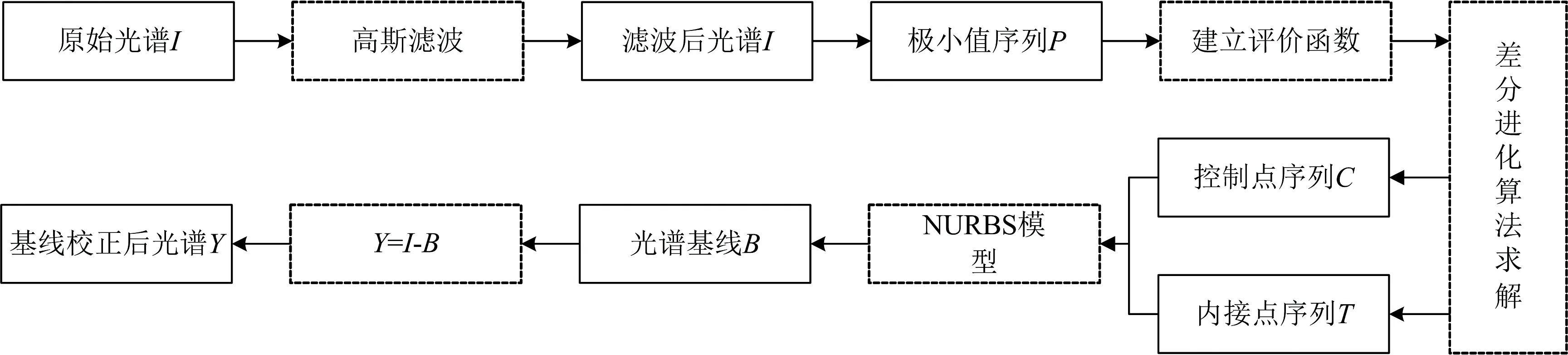
图1 基线校正流程
1.2 光谱预处理
在ICP-AES测量过程中,受杂散光影响,光谱中包含大量噪声信号,严重影响基线拟合过程中波谷点的选择,因此在进行基线拟合前首先需进行预处理以消除噪声。本文采用高斯滤波对ICP-AES光谱进行预处理。高斯滤波是数字信号处理中常用的滤波方式,其本质为原始信号与高斯卷积核的离散卷积运算,如式(1)所示。
(1)
式(1)中,f可视为原始信号,g可视为高斯卷积核。由于ICP-AES光谱信号基本服从高斯分布,因此通过高斯卷积核进行卷积能够尽可能地保留谱线信息,避免降低光谱分辨率;另一方面,本文对实测的ICP-AES光谱数据进行分析,抽样统计不同波段中的噪声信号分布特征,拟合噪声数据的概率密度函数以及概率分布,如图2和图3所示,根据统计结果可知,ICP-AES光谱中噪声信号概率密度函数基本服从高斯分布,因此认为通过高斯滤波能够较为有效地去除噪声信号。
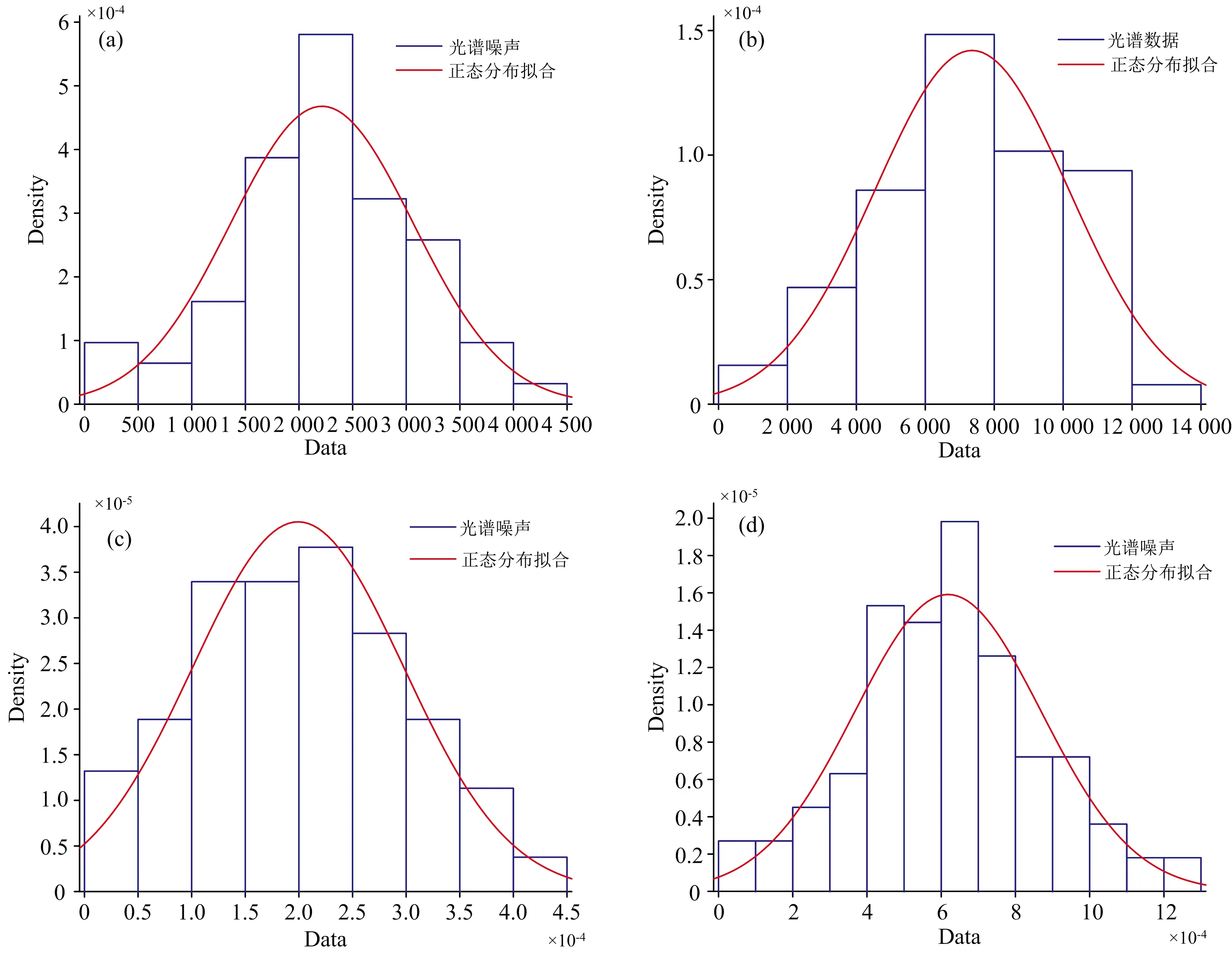
图2 光谱噪声信号概率密度
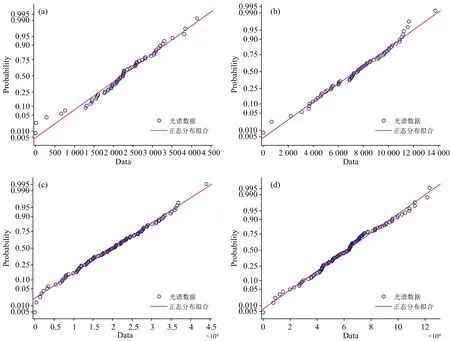
图3 光谱噪声信号概率分布
1.3 建立光谱基线模型
本文采用非均匀B样条曲线模型进行基线拟合。非均匀B样条曲线常用于自由曲线和曲面的构造,具有良好的低阶光滑性,因此同样适用于拟合光谱基线。记数据点序列集合为X,X={(x1|u,x1|v),(x2|u,x2|v),(x3|u,x3|v), …,(xn|u,xn|v)},采用节点符号t将数据点序列X进行划分,并记节点序列集合为T,T=[t-k+1,t-k+2, …,t-1,t0,t1, …,tn,tn+1,tn+2, …,tn+k],则节点序列满足式(2)关系
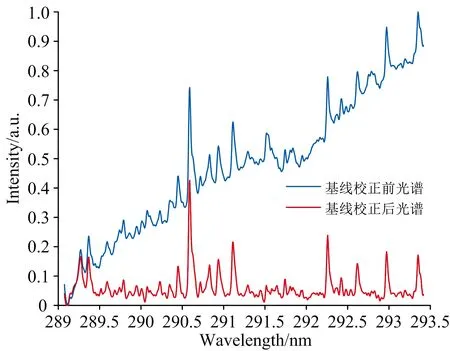
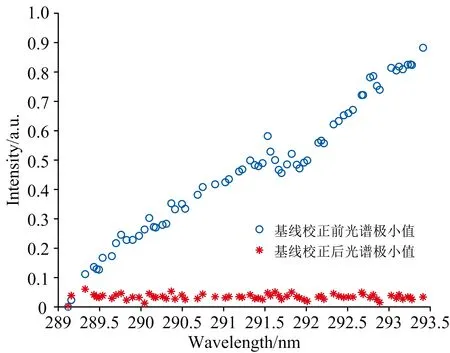
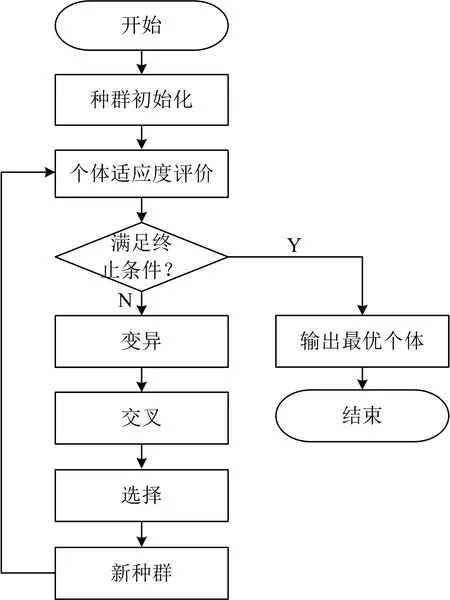
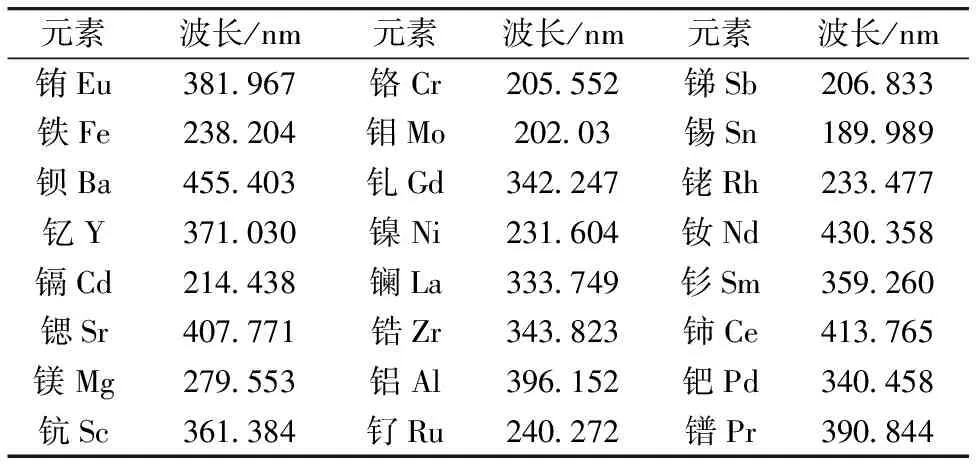
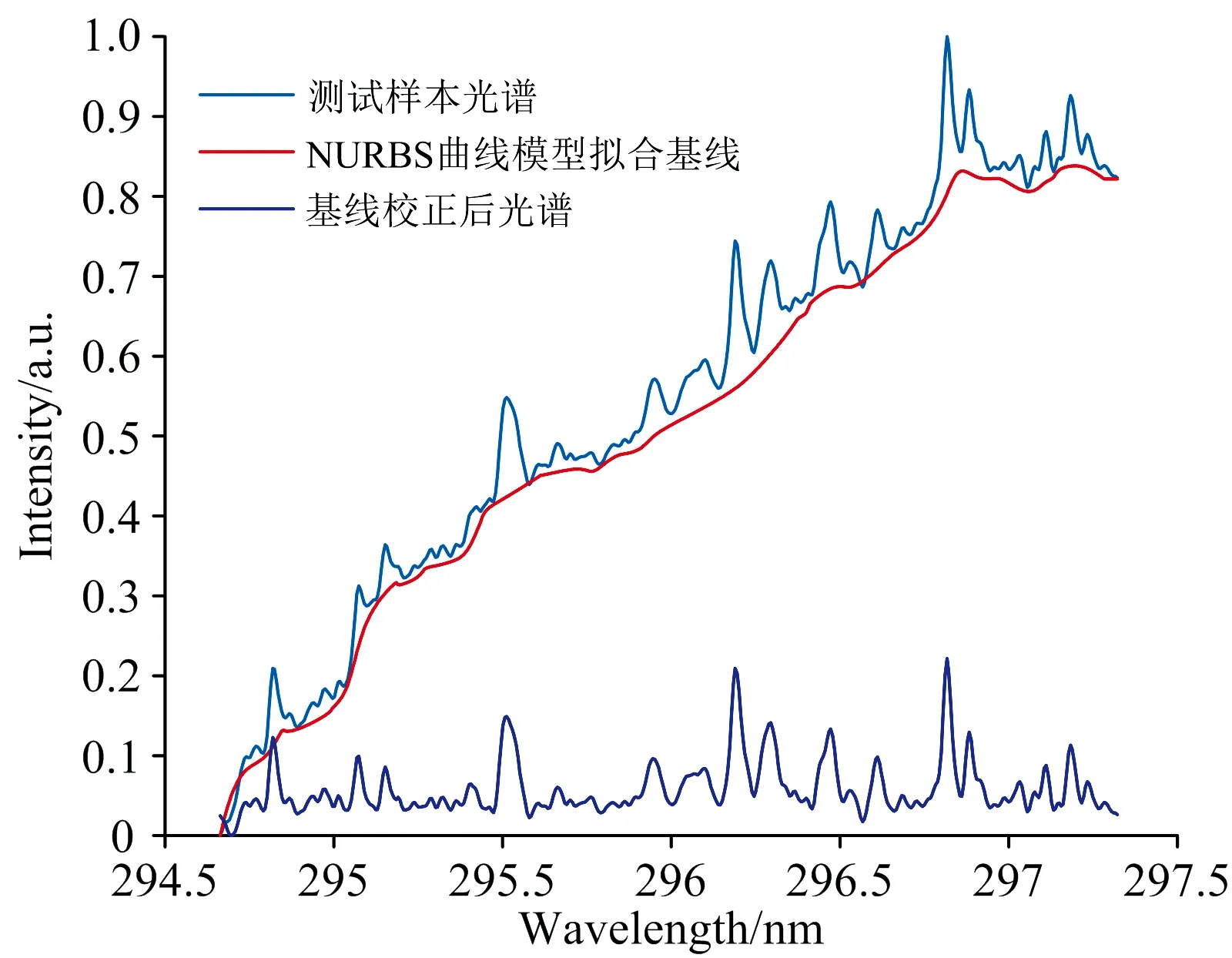
t-k+1≤t-k+2≤…≤t-1≤t0 (2) 式(2)中,t1到tn称为内节点,其余称之为外节点,n为内节点数,k为B样条曲线的阶数;若内节点均匀分布,则最终构成的曲线称之为均匀B样条曲线,反之则为非均匀B样条曲线。 对于k阶的B样条曲线,其表达式如式(3)所示。 (3) (4) 在计算过程中,控制点序列和曲线坐标点序列通常均以坐标的形式进行运算,因此式(3)也可写为 (5) 同理,可记控制点序列为C={(c0|u,c0|v),(c1|u,c1|v), …,(cn|u,cn|v)}。 根据1.3节NURBS曲线的定义可知,控制点序列C和内接点序列T直接决定了NURBS曲线的分布,因此若采用NURBS曲线模型拟合光谱基线,则需要寻找一组合适的控制点序列C和内接点序列T,若控制点序列C和内接点序列T的选取不恰当,将会直接影响最终基线校正的结果。 依靠专家经验和光谱分布情况进行控制点序列C和内接点序列T的选取一方面效率较低,另一方面其选择结果也难以保证最终光谱基线校正的效果,因此本文建立了ICP-AES光谱基线校正评价函数,该评价函数基于NURBS曲线建立,并以光谱基线校正前后极小值的分布特征为评价指标,通过求解评价函数的全局最优解即可得到合适的控制点序列C和内接点序列T,有效改善了NURBS曲线的应用效率,同时也提高了控制点序列C和内接点序列T选取的准确性。 基线校正前和基线校正后,光谱及其极小值点分布差异如图4和图5所示。 图4 基线校正前后光谱信号 图5 基线校正前后光谱极小值 根据基线校正前和校正后的光谱信号可知,光谱数据点中的极小值序列的分布发生了明显变化,显然,基线校正前,光谱数据点中极小值序列的离散程度更高,基线校正后,光谱数据点中的极小值序列的离散程度更低,分布更加接近极小值序列的算术平均值。 根据标准偏差的数学定义可知,标准偏差常用于度量数据分布的离散程度,用以衡量数据值偏离算术平均值的程度,因此可以利用光谱数据点中极小值序列的标准偏差值作为光谱基线校正程度的度量准测,以此来建立光谱基线校正评价函数,达到基线校正的目的。 设滤波处理后且未校正基线的光谱强度值服从模型I′(x),基线校正后的光谱强度值服从模型I(x),本文采用非均匀B样条曲线拟合光谱基线,因此设基线模型为B(C,T);由于光谱强度值的叠加可视为线性叠加,因此上述模型满足如式(6)所示的关系: I(x)=I′(x)-B(C,T) (6) 设光谱中极小值序列集合为P,P={(p0,I′(p0)),(p1,I′(p1)), …,(pn,I′(pn))},并记PX={p0,p1, …,pn},PY={I′(p0),I′(p1), …,I′(pn)},经基线校正后,集合PX对应的校正强度值集合为IY,IY={I(p0),I(p1), …,I(pn)}。 以校正强度值集合IY的标准偏差为度量准测,建立评价函数,如式(7)所示。 F(C,T)=STD({I(p0),I(p1),…,I(pn)})= STD({I′(p0)-yv|yu=p0,I′(p1)-yv|yu=p1,…, I′(pn)-yv|yu=pn}) (7) 式(7)中,yu和yv定义与式(5)中定义相同,均表示NURBS曲线横、纵坐标,STD表示计算集合的标准偏差。因此,光谱基线校正问题可以转换为,确定一组合适的C、T取值,使得F(C,T)取值达到最小,即,针对F(C,T)进行全局寻优的问题。而在全局寻优方面,差分进化算法则能够快速准确的达到上述目标。 根据1.4节内容可知,本文提出的ICP-AES光谱基线校正方法可以转换为求解评价函数的全局最优解。遗传算法在全局寻优问题上往往能够获得较为理想的效果,本文采用基于遗传算法改进的差分进化算法求解式(7)的全局最优解。 差分进化算法主要包括种群初始化、变异、交叉和选择四个步骤。种群初始化后,循环执行变异、交叉和选择操作,直到达到最大进化代数;在每一轮进化中对种群所有个体向量执行变异操作,得到变异向量;然后将变异向量与个体向量进行交叉操作,得到交叉向量;最后对比交叉向量与个体向量的适应度,选取适应度较小的向量作为下一代种群的个体向量。差分进化算法流程如图6所示。 图6 差分进化算法流程图 (1)种群初始化 记种群个体向量为X=[x1,x2, …,xD],其中D为个体向量维度;设定种群个体向量中各参数搜索范围,并生成最大个体向量和最小个体向量,如式(8)所示。 (8) 通过初始化生成NP个向量,表示种群的所有个体,则第G代种群中第i个个体向量可表示为 (9) 个体向量中第j个参数的生成规则如式(10)所示。 j=1,2,…,D (10) (2)个体适应度评价 将当前进化代数内所有的个体向量Xi, G代入适应度函数F(·),输出的结果F(Xi, G)为个体的适应度值,适应度值越小,则相应的个体越优。 (3)变异 每一轮进化中,对当前进化代数G下的所有的个体向量Xi, G执行变异操作得到变异向量Vi, G。本文采用DE/rand/1/bin变异算子,其表达式如式(11)所示。 Vi,G=Xir1,G+SF(Xir2,G-Xir3,G) (11) 式(11)中,ir1,ir2和ir3为当前进化代数内种群中的三个随机个体向量索引,且必须满足ir1≠ir2≠ir3,SF为[0, 1]内的常数,表示缩放因子。 (4)交叉 将所有个体向量Xi, G与对应的变异向量Vi, G的信息成分交叉互换,得到交叉向量Ui, G。交叉规则如式(12)所示。 (12) 式(12)中,CR为(0, 1)内的常数,表示交叉概率,jrand为[1,D]内的随机整数,表示随机交叉参数索引。 (5)选择 将所有个体向量Xi, G和交叉向量Ui, G代入适应度函数进行比较,选择适应度较小的向量作为下一代进化的新个体向量,如式(13)所示。 (13) 2.1.1 测试数据来源 本文搭建一台CCD型扫描式ICP-AES光谱仪,并利用该光谱仪扫描一组样品溶液对应的ICP-AES光谱信号,该溶液所含元素及各元素对应的特征波长如表1所示。 表1 样品溶液所含元素及特征波长 选取其中的294.547~297.400 nm的光谱作为原始样本并进行归一化处理,如图7所示;对原始样本进行高斯滤波处理,消除高频噪声,并作为最终的基线校正测试样本,如图8所示。 图7 原始样本光谱信号 图8 测试样本光谱信号 2.1.2 基线校正模型特征参数取值范围 由1.4节和1.5节内容可知,利用差分进化算法求解本文所建立的光谱基线校正评价函数时,首先要确定出评价函数中特征参数的取值范围,即控制点序列C和内接点序列T的取值范围。 由于控制点序列C和内接点序列T的取值范围决定了评价函数全局最优解的分布区间,进而决定了NURBS曲线的趋势,因此对最终基线拟合结果的影响较大。本文为保证基线拟合结果的可靠性,充分利用差分进化算法全局寻优的能力,以及本文建立的评价函数的优点,设定内接点序列T和控制点序列C的取值范围为有效取值区间内的最大范围。对于NURBS曲线,内接点序列T的有效取值区间为[0, 1],故本文继续采用该取值区间作为差分进化算法的搜索范围;而对于控制点序列C,本文则以样本光谱信号的最小值和最大值分别作为取值区间的临界值。 2.2.1 差分进化算法计算结果 设定差分进化算法初始条件,取NP=100,G=60,进行迭代运算,最终计算完成后,控制点序列C分布如图9所示,内接点序列T分布结果如图10所示。 图9 控制点序列C分布 图10 内接点序列T分布 2.2.2 NURBS曲线拟合结果 根据计算出的控制点序列C和内接点序列T拟合对应的NURBS曲线作为测试样本的光谱基线,并对样本进行基线校正,得到校正后的光谱,如图11所示。 图11 测试样本光谱、拟合基线和基线校正后光谱 2.2.3 不同噪声情况下基线拟合结果对比 在本文提出的基于差分进化算法和NURBS曲线模型的ICP-AES光谱基线校正方法中,基线拟合效果和基线校正效果一定程度上受噪声分布影响;当噪声未充分消除时,测试样本光谱信号中极小值点序列的密度将会增大,导致最终在拟合基线的过程中存在一定程度的过拟合现象,如图12所示。 图12 噪声未充分消除时基线拟合情况及基线校正情况 而通过高斯滤波或其他滤波方式消除噪声时,若滤波效果过于激进,则一定程度上可以避免过拟合现象,但同时则可能会导致测试样本光谱信号时域分辨率下降,波峰波谷出现失真,最终影响基线拟合效果和定性定量分析效果。 因此在实验过程中,若存在噪声干扰较为复杂的情况,可以通过专家判定方式,视情况选定极小值序列P的取值,并建立评价函数进行求解,从而获得较好的基线校正和基线拟合结果。 提出了一种基于差分进化算法和NURBS曲线模型的ICP-AES光谱基线校正方法,该方法依据基线校正前和基线校正后光谱信号的特征变化以及NURBS曲线模型建立评价函数,并通过差分进化算法进行求解,计算出适当的内接点序列T和控制点序列C,进而拟合出合适的光谱基线,达到基线校正的目的。 本文提出的方法不仅能够充分利用NURBS曲线的自身优势拟合出不同类型的光谱基线,同时也能够利用差分进化算法全局寻优的特点计算出合适的内接点序列T和控制点序列C,极大的提高了NURBS曲线的应用效率,也改善了NURBS曲线应用于光谱基线校正领域时内接点序列T和控制点序列C难以确定的局限性。但本文所提出的方法仍具有一定的不足之处,例如当光谱信号中噪声较为复杂时,可能会出现基线过拟合现象,此时仍然会引入部分人为工作量,因此在后续的优化中,将针对以上问题进行重点研究,进一步提高NURBS曲线在光谱基线校正过程中的应用效率。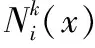
1.4 建立ICP-AES光谱基线校正评价函数
1.5 求解评价函数全局最优解
2 结果与讨论
2.1 测试方案
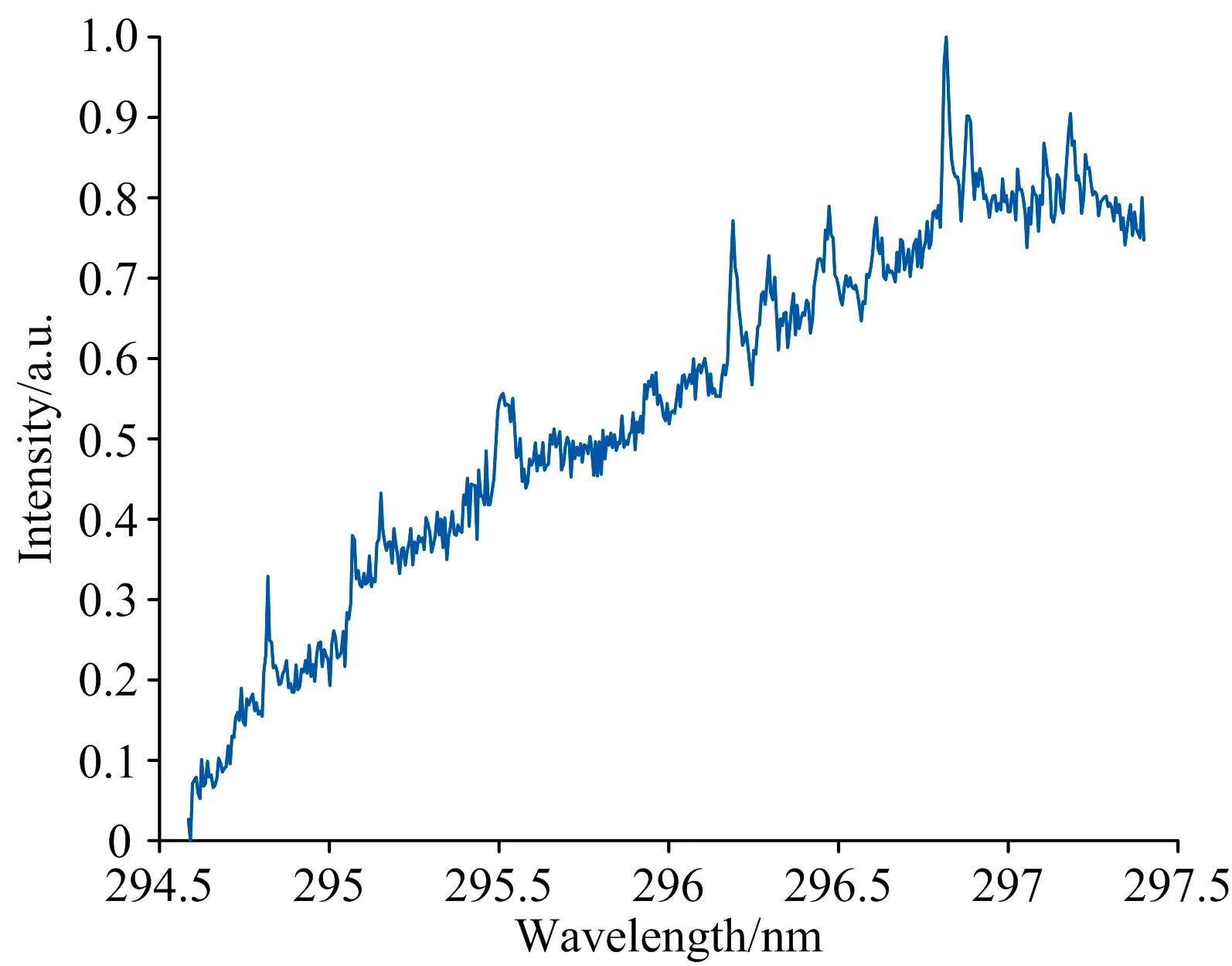
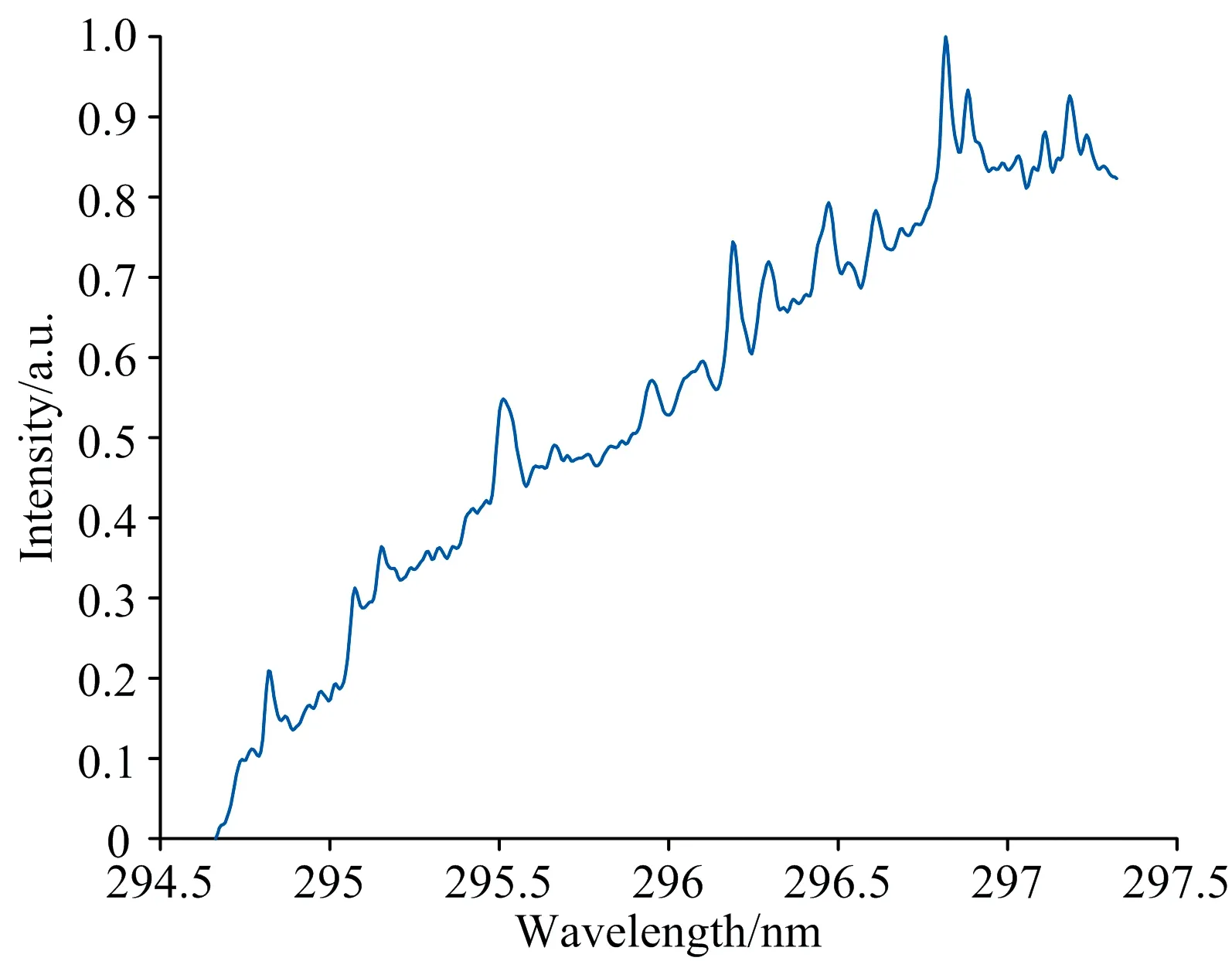
2.2 测试结果
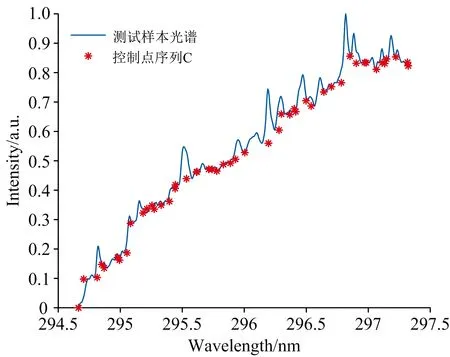
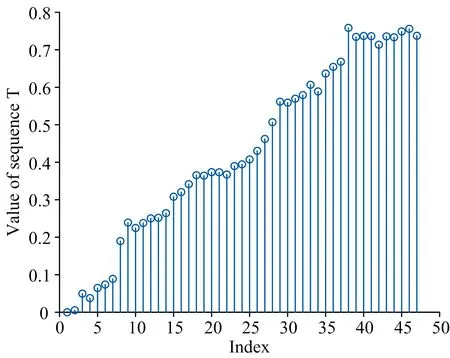
3 结 论

