基于改进支持向量机的超声参数与受载混凝土应力状态研究

杨雅勋， 张伟德， 于海波， 柴文浩， 刘德闯

(1.长安大学 公路学院，西安 710064； 2. 长安大学工程设计研究院有限公司，西安 710064)

超声波检测作为无损检测方法之一，常被用于评价混凝土结构的缺陷、强度、密实度、应力等。其主要是通过超声波在混凝土结构中传播过程的超声参数特征来判断混凝土结构的状态。

目前国内外针对该方法的研究也在不断地深入。1953年，Hughes等[1]提出了声弹性理论将超声波应用于固体材料中。Demirboa等[2]研究了超声波波速和混凝土强度之间的相关性。赵岩等[3]通过钢筋混凝土结构的超声波检测试验，研究了不同类型的钢筋混凝土构件在不同应力状态下超声波波速的变化，拟合了钢筋混凝土构件的拉应力和超声波声速的关系。Liu等[4]在单轴加载条件下，研究了混凝土波速与应力的关系，并采用最小二乘法拟合了波速与单轴应力的函数关系式。朱金颖等[5]采用波速、主频和幅值等多因素判别的方法，探讨了超声参数与应力的关系，并且定义了损伤系数。但是，单一的超声参数与应力关系的曲线拟合效果较差，混凝土内部材料力学性能的非线性和结合面的不均匀性限制了超声波技术在识别混凝土应力方面的应用，需要一种更具适用性和精确的方式来拟合超声参数与应力的关系。采用机器学习来分析，是一个自然而然的想法。作为机器学习的经典算法，支持向量机(support vector machine，SVM)[6-9]适合于分析小样本和多维数据问题，常被用于分类和预测。黄昕[10]采用SVM有效地利用影像的纹理、结构、尺度和对象信息，弥补了遥感影像光谱特征的不足。程灿等[11]将SVM和粒子滤波法相结合用于刀具磨损状态的识别，精确地识别了刀具的磨损量。胡晓依等[12]结合SVM分类器搭建了适用于滚动轴承故障诊断的改进型深度卷积神经网络模型，极大地提升了轴承故障识别准确率、模型收敛速度和泛化能力。Nieto等[13]使用混合粒子群方法优化了SVM，并将其应用于航天器发动机剩余寿命的预测。

本文采用支持向量机的方法，结合波速、首波幅值、主频幅值、非线性系数和超声波谱面积5个超声特征参数对混凝土损伤全阶段进行应力定量分析。

1 超声波识别混凝土应力

根据声弹性理论[14]，超声波作为高频的弹性波，在有应力的固体材料中的传播速度不仅取决于材料的二阶弹性常数，还与高阶弹性常数和应力有关。而混凝土材料的二阶、三阶材料弹性常数很难求得。由于混凝土的非均匀性和各向异性，超声波在传播过程中，在每一个随机分布的砂石表面都要发生复杂的反射、透射和衍射等现象，要精确描述混凝土内部的传播路径是非常困难的。只能从宏观角度出发，将混凝土内部具有一定尺度的缺陷体认为是异常体，观测超声波通过这些异常体时的异常表现来判断混凝土内部的质量状况。弹性波可以用波的振幅、频率、相位、波速、偏振状态、衰减程度等特征来描述其特性。

大量的试验研究[15-21]表明，材料内部结构局部软化或裂缝的出现，都会导致非线性超声参数极大的改变，传统的方法通过声时、声速判断混凝土结构的应力状况存在较大的局限性。非线性所表现出的超声特性对细微的损伤更加敏感；超声波首波幅值反映了混凝土的塑性特性；主频幅值随应力比变化规律表征了超声波在混凝土内部传播完成后的能量剩余；超声波谱面积表征了超声波传播过程中携带的能量。为了更加准确地判断混凝土内部状况，需要尽可能多地采集对缺陷敏感的超声参数，建立合适的模型来模拟混凝土应力与超声参数的关系。因此，将采集的超声数据进行时域和频域分析，选取对应力变化反映明显的多种超声特征参数，采用支持向量机对多种超声参数与混凝土损伤全阶段的应力进行定量分析。

2 改进支持向量机

2.1 支持向量机

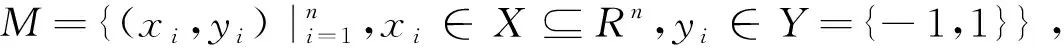
对于超声参数与混凝土应力这一非线性问题，首先通过一个非线性映射φ，将样本数据从原空间Rn映射到一个高维的特征空间F，在此高维特征空间求最优分类面[23]。为了降低计算复杂度，需避免直接计算非线性映射φ，可引入满足Mercer条件的核函数[24]K(xi,xj)=〈φ(xi)φ(xj)〉在原空间上进行φ的内积运算，这样在原空间分类面为w·φ(x)+b=0。此时，使分类间隔2/‖w‖2最大的分类面即为最优分类面，问题转化为以下在约束条件下求函数极小值

(1)

式中：w为分类面的权系数向量；b为分类面的阈值；松弛项ζi≥0，用于修正数据因噪声而偏离同类点；C为惩罚参数，用于调节学习机器的置信范围和经验风险比例。这是一个凸二次优化问题，能够保证找到的极值解就是全局最优解。利用Lagrange函数可将上述最优分类面问题转化为对偶问题

(2)

根据Kuhn-Tucker条件，系数αi必须满足αi{yi[w·φ(xi)+b]-1+ζi}=0。由于非支持向量的数量远多于支持向量，因此多数αi=0，只有极少数αi≠0。

依照式(2)求得系数ai后，给定一组测试样本超声参数x，通过判别函数式(3)来判断x所属的类别。

(3)

不同的核函数得到的分类和预测结果也不相同，常用的核函数有线性核函数、多项式核函数、径向基核函数和Sigmoid核函数。如实际工程中常用的核函数为径向基核函数，表达为K(x,xi)=exp(-g‖x-xi‖2)，g为一个正实数，以此为核函数的支持向量机中有两个参数，惩罚参数C和核函数参数g。

2.2 支持向量机参数的优化及数据处理

惩罚参数C和核函数的选取非常明显地影响着支持向量机的性能，选择合适的参数尤为重要。针对超声参数与应力关系这一问题，罕有能够借鉴的经验。为了尽可能准确地描述二者关系，采用遍历算法和粒子群优化算法对惩罚参数和所选取不同种类核函数的参数进行优化。

遍历算法是指沿着某条搜索路线，依次对树中每个节点均做一次且仅做一次访问，访问节点所做的操作依赖于具体的问题。对于本文问题，给定参数一定范围值和计算步长，对节点上的参数值都进行支持向量机，以均方误差MSE作为目标函数，选择使均方误差最小的参数进行后续的支持向量机模拟。

粒子群优化算法(particle swarm optimization,PSO)[25]是Kennedy模拟鸟群迁徙和群聚行为而提出的基于群体智能的全局随机搜索算法。在解决实际优化问题时，假定问题的解对应于每一个粒子在搜索空间中的位置，每一个粒子都由其速度vi，xi位置和适应度来决定，在解空间中采用适应度来衡量粒子的优劣。

假定这些粒子在空间中运动，群体规模为n，群体的每个粒子i(1≤i≤n)，有以下属性：粒子自身的当前最优位置pi，所有粒子的当前最优位置pg。每个粒子更具下面的公式更新自己的速度和位置

(4)

式中：w为惯性因子，用于调节搜索范围，w越大全局寻优能力越强，但局部寻优能力越弱；k为当前迭代次数；c1c2为学习因子，用于调节学习的最大步长，为非负常数；r1,r2为分布于[0,1]的随机数，用于增加搜索的随机性。

采用PSO进行参数优化时，将支持向量机预测结果的均方误差MSE作为粒子群算法的适应度函数。那么利用PSO优化支持向量机算法过程，如图1所示。

除了惩罚参数和核函数，分类器的分类能力还受数据属性值大小的影响，过大的属性值使得分类器最终得出的分类超平面过于陡峭，分类能力减弱。为了提高决策函数的优化效果，消除指标之间的量纲影响、平滑数据的波动性，需要对数据进行归一化处理来。考虑到混凝土材料的特殊性，提出了首项归一化，即以无应力阶段测得的数据为1对数据进行归一化处理，并对比了不同归一化方式的效果。

3 模型仿真分析

通过有限元软件建立二维混凝土塑性损伤模型[26]，来模拟超声波在受载混凝土中传播的过程。选取随应力变化明显的超声参数，并用不同的归一化方式和核函数对采集的数据进行分析，选择模拟效果最好的归一化方式和核函数进行后续优化。

考虑到混凝土的非均质性，将二维模型分为骨料、砂浆、骨料与砂浆间的相邻界面。按连续骨料级配理论，生成粒径小于40 mm的圆形骨料C40混凝土模型，尺寸为150 mm×150 mm。在ABAQUS有限元软件中，将赋予材料参数的模型划分为1.45 mm×1.45 mm的网格单元，共14 094个单元，如图2所示。约束模型的下边界，在上边界上采用位移加载模拟进行60 kN/级的分级加载至900 kN。同时，以混凝土模型左下角为坐标原点(0,0)，在模型的(0,75 mm)处进行超声激励，(150 mm,75 mm)处进行信号接收，布置如图3所示。发射声波采用能量较为集中的HANNING窗口调制的更接近超声换能器发出的脉冲信号，信号长度2个周期，频率为100 kHz，信号图如图4所示。

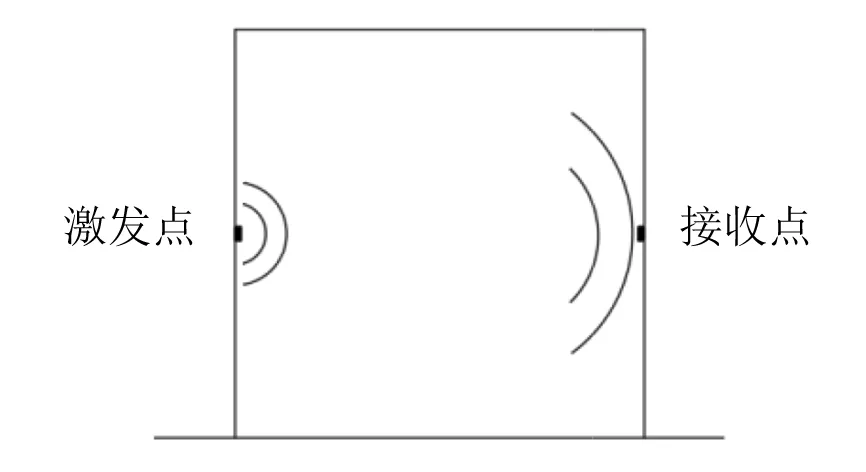
图3 信号激发点和接收点布置图Fig.3 Layout of signal excitation and reception points

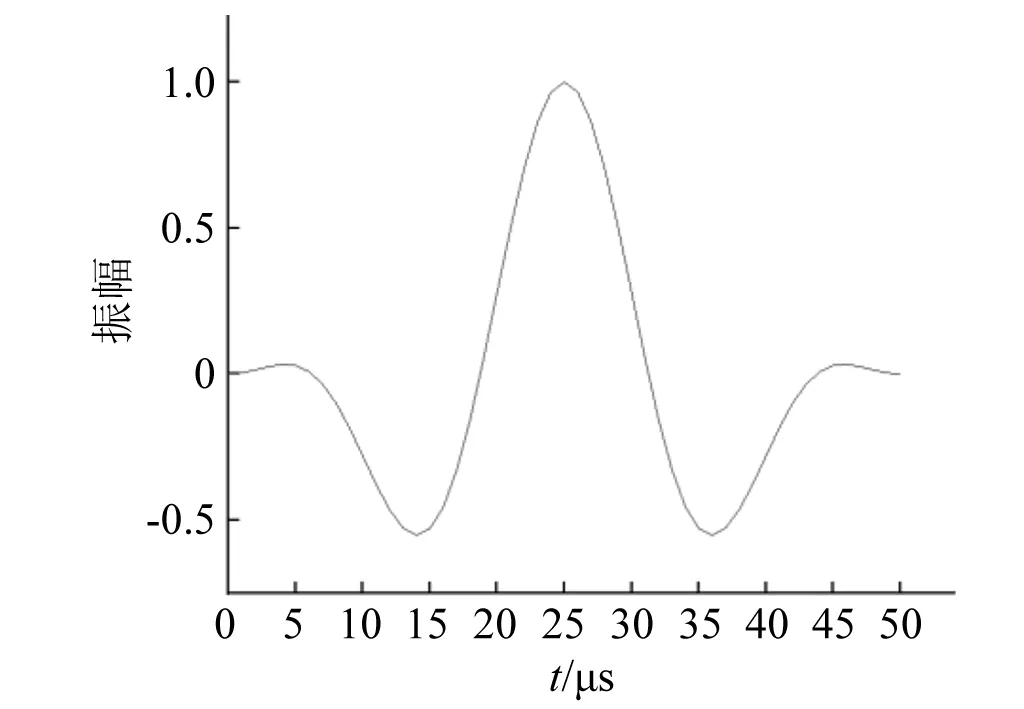
图4 激励源信号Fig.4 Excitation source signal

完成加载后将采集的数据进行时域频域分析，得到反映混凝土内部结构应力状态的超声参数。最终选择波速、首波幅值、非线性系数、主频幅值和波谱面积这5个随应力变化呈规律性且较为敏感的参数以零应力状态为1进行归一化处理后，得到以下五种超声参数与应力的关系如图5所示。

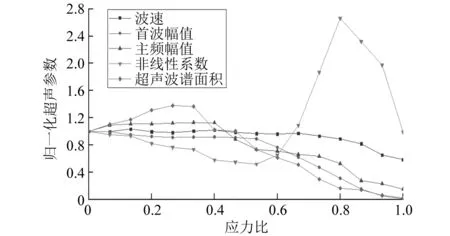
图5 超声参数与应力关系Fig.5 Ultrasonic parameters in relation to stress

用单一的超声参数来判断混凝土材料的应力是比较单薄的。将以上五种超声参数作为自变量，应力作为因变量，采用支持向量机来模拟五种参数与应力的关系。为避免随机骨料的存在对结果产生影响，共建立20个随机骨料模型。选择19个模型的304组超声参数数据作为训练集，剩余一个模型的16组数据作为测试集，用训练集对支持向量机模型进行训练，再用得到的模型对测试集进行预。取惩罚参数C=2，核函数参数g=1，以决定系数R2和均方差MSE作为目标函数。结果如下：

(1)采用不同归一化方式的对比

在MATLAB软件中建立好支持向量机模型，对数据进行不同的归一化预处理并与未归一化处理的结果进行对比，为直观的体现结果的差异减小核函数的影响，核函数均采用线性核函数，最后得到的结果如图6所示。

图6 不同归一化结果图Fig.6 Graphs of different normalisation results

从图6中可以看出，经过归一化处理后的结果明显优于未归一化处理的，其原因是数据的属性值会影响分类能力，波动过大的属性值导致分类面过于陡峭、分类能力减弱；模型在低应力阶段的模拟效果并不好，这是由于为直观对比归一化处理对结果产生的影响，采用的核函数为线性核函数K(x,xi)=φ(x)Tφ(xi)缺少核函数参数，特征空间与输入空间维度相同，此时会出现“欠学习”现象；从表1可以看出，对超声参数的数据样本进行归一化的预处理后，能提高回归预测的决定系数，减小均方误差；采用首项归一化方式比其他归一化方式结果精度有提高，更适用该问题。

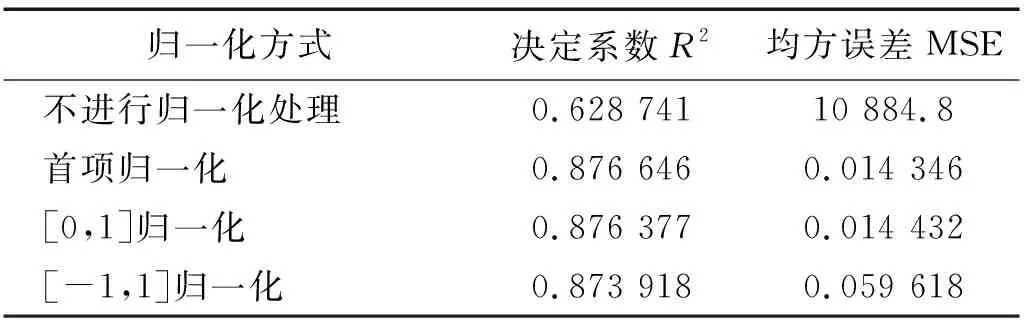
表1 采用不同归一化方式对比Tab.1 Comparison using different normalisation methods

(2)采用不同核函数的对比

对于混凝土超声参数与应力这一非线性问题需要选择合适的核函数。采用首项归一化方式和不同的核函数，最后得到测试集评价指标。结果如图7所示。

图7 不同核函数结果图Fig.7 Plot of results for different kernel functions

从图7可以看出，不同的核函数在模拟超声参数与混凝土应力时效果相差较大。采用多项式和径向基核函数的结果优于线性和Sigmoid核函数的结果；径向基核函数属于局部核函数抗干扰能力强，模拟的效果也最优；多项式和Sigmoid核函数属于全局核函数，插值能力较弱，当数据中波动大时，预测结果波动亦大；从表2可以看出，采用径向基核函数的模型准确度更高，最终预测效果最好。

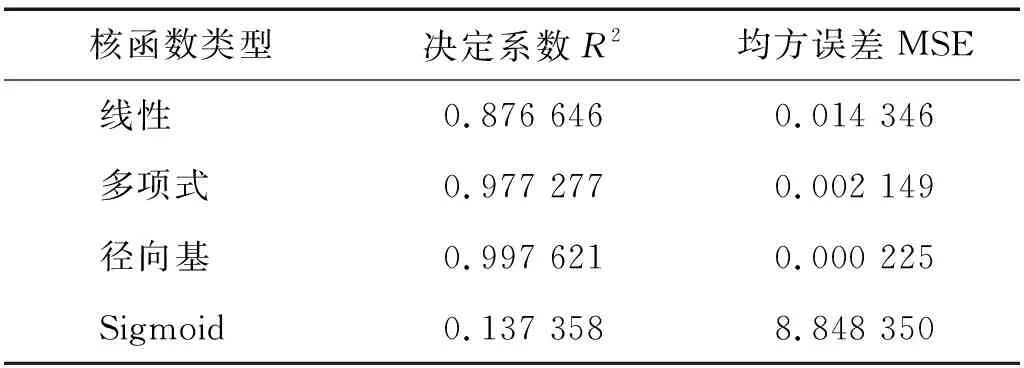
表2 采用不同核函数对比Tab.2 Comparison using different kernel functions

4 试验验证

4.1 试验材料参数与测试加载

试验共设计20个尺寸为150 mm×150 mm×150 mm的C40混凝土立方体试件，水泥选用P.O42.5，水灰比为0.49，细骨料的粒径为5～20 mm，粗骨料粒径选择20～40 mm，细骨料与粗骨料的骨料比为0.45；配合比如表3所示。

表3 混凝土材料配合比Tab.3 Concrete material mixes

正常环境养护试件28天之后。采用压力机对混凝土试件按60 kN/级进行分级加载，加载至720 kN时，采用30 kN/级进行加载，直至试件破坏，记录每级数据。在试验过程中，加压到900 kN时大部分试件还能够继续承压，不同试件达到不能继续加压的峰值压力也不尽相同，考虑所有试件的峰值压力，对超过1 140 kN压力的数据不再进行分析。因此包括无应力状态在内分级加载共分为27级。加载示意图及破坏图如图8和图9所示。

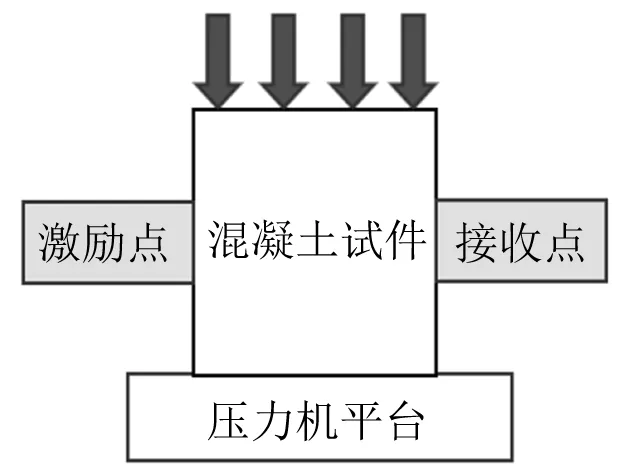
图8 加载示意图Fig.8 Loading diagram

图9 试件形成贯通裂缝破坏Fig.9 Through-crack damage to specimens

4.2 试验结果分析

按照试验方案，完成20个试件的加载。由于有一个试件加载尚未达到900 kN就被压碎不能继续加载，舍弃此试件的数据，对剩余的19个试件的数据首项归一化后采用支持向量机法进行分析。

4.2.1 简单支持向量机

给定初始参数C=2,g=1。取18个试件486组数据作为训练集，剩余一个试件27组数据作为测试集，得到的支持向量机结果如图10所示。

图10 简单支持向量机结果Fig.10 Simple support vector machine results

结果显示，其决定系数为0.506 445，均方误差为0.048 149，误差水平显著，特别是在低应力阶段，预测误差很大，试验结果与数值模拟结果相比较差别较大。其原因是试验试件相较于有限元模型存在微裂隙，在受压初期微裂隙会闭合从而导致超声信号发生改变，而由于混凝土试件内部材料的随机性，微裂隙的分布也具有随机性；同时，换能器采集的超声数据存在人为误差。这些因素导致了超声参数产生不可控的波动，从而影响模拟效果。

4.2.2 遍历算法优化支持向量机

C过小会导致模型预测效果差，过大又会导致模型过拟合泛化能力减弱，而降低g又会影响支持向量的个数。显而易见的是，初始参数是按经验取值不是最优取值，进行模拟时会出现“欠学习”或“过学习”的现象，预测值和真实值拟合效果差。因此，采用遍历算法对一定范围内的参数C和g都进行支持向量机，以MSE作为目标函数，选择使得MSE最小的C和g作为最优参数进行支持向量机。过程如下：

(1) 取参数C和g的变化范围均为[2-8，220]，步长均为p；

(2) 将训练集均分为18个子集，选取其中一个子集数据作为测试集，其余的17个子集作为训练集，共选择18次，一共得到18个模型；

(3) 将18个模型所得到的均方误MSE差求平均值，以此作为目标函数，选择使得MSE最小的参数C和g。足够小的步进能够求得更优的参数，但会导致运算时间过长。先取步长为1，绘制出参数粗略选择的结果图11(a)，在此基础上确定使得MSE较小的范围，C的范围缩小至[2-2，28]，g的范围缩小至[2-3，23]。将以上范围重新作为遍历范围，步长取0.1，再次进行遍历运算，绘制结果图11(b)。最终求得运算结果为C=1.049，g=0.048 5，以此参数进行支持向量机，得到的结果如图12所示。

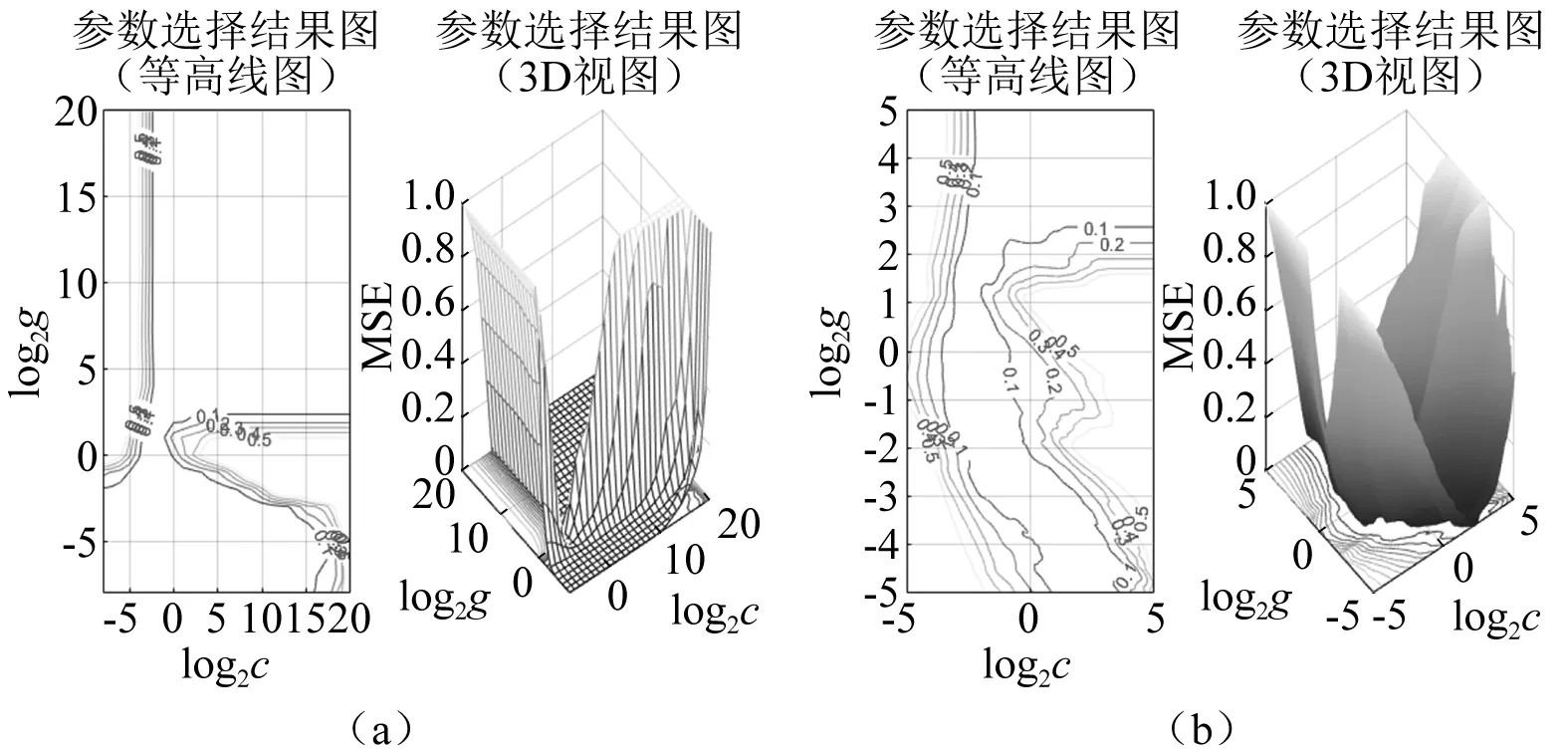
图11 参数粗略选择结果图Fig.11 Graph of results for rough parameter selection

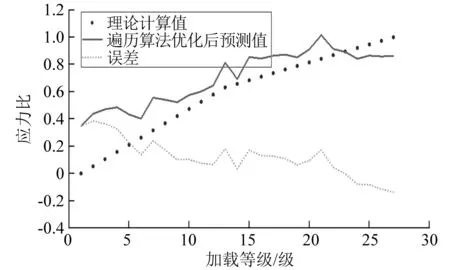
图12 遍历算法优化后支持向量机结果Fig.12 Graph of results for rough parameter selection

其决定系数R2为0.705 270，均方误差MSE为0.033 232，结果明显优于参数未经优化的结果。由于微裂隙的随机性和超声数据接收时可能存在的误差，在低应力阶段预测的误差仍然较大，但是预测结果一般都比真实应力高偏于安全；当加载等级超过20级时(F=930 kN)，试件已经形成或将要形成较为明显的裂缝，超声信号变化大，预测的结果波动亦大。

4.2.3 粒子群算法优化支持向量机

经过粒子群算法优化后，得到的结果为C=0.570 382，g=0.205 898，以此参数进行支持向量机，得到的预测结果如图13所示。

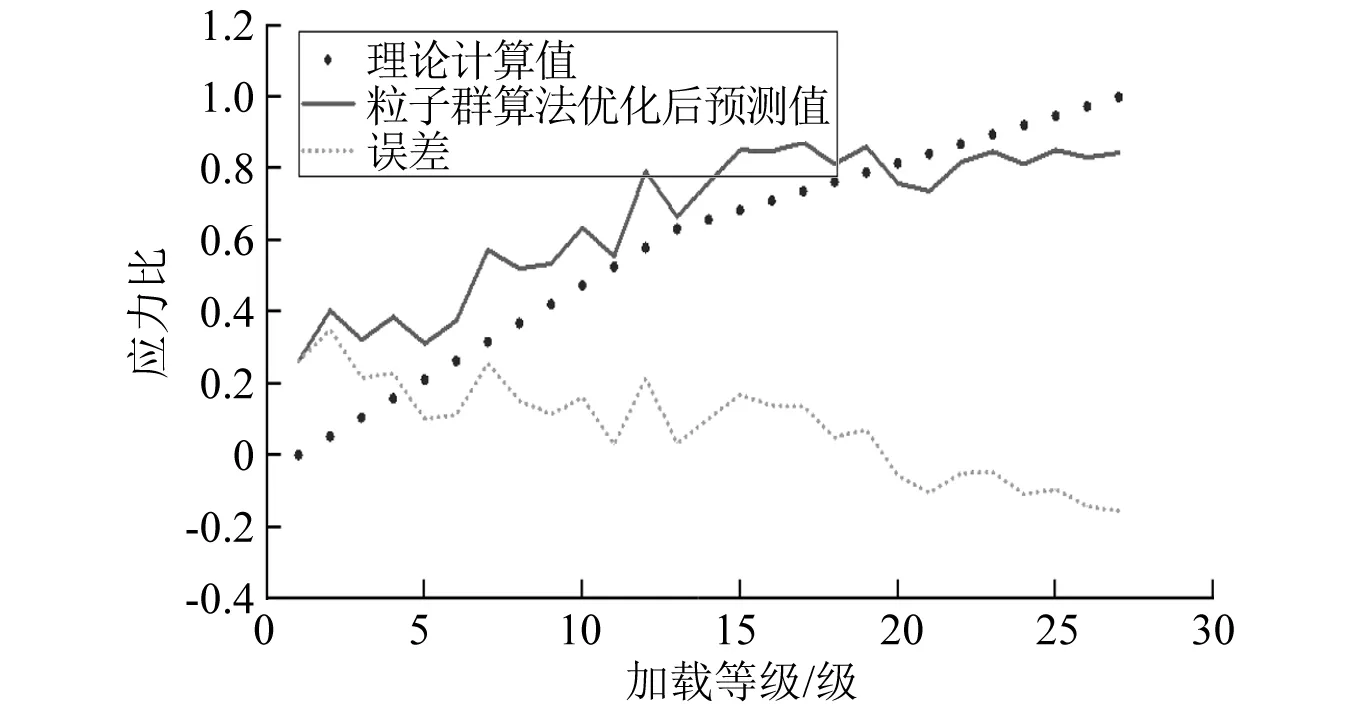
图13 粒子群算法优化后支持向量机结果Fig.13 Support vector machine results after particle swarm algorithm optimization

其决定系数R2为0.768 472，均方误差MSE为0.026 319，预测得到的应力结果一般都比较偏高。只有在加载超过20级时，预测结果偏低，而此时应力已经超过了对应材料的混凝土立方体抗压强度，从混凝土表面已经能够观察到较为明显的细微裂缝，此时已经基本不需要通过超声波来判别混凝土内部应力。粒子群算法优化后的模型得到的结果决定系数最高，均方误差最小，与遍历算法相比大幅减少了运算时间，模拟的结果效果最好。

5 结 论

本文通过模型仿真和试验验证的方法，对混凝土试件进行分级加载，测试了不同应力状态下的超声参数。采用支持向量机的方式，模拟了超声参数与应力的关系。主要得出以下结论：

(1)采用支持向量机模拟超声参数与应力的关系，对数据进行归一化预处理后，得到的模拟效果优于未进行归一化处理的模型；采用首项归一化的方式进行预处理的数据得到的模型模拟的效果明显优于最值归一化和中值归一化的模型。

(2)对比选用不同核函数模拟的模型，发现采用径向基核函数的模型模拟效果最优。

(3)试验表明，在低应力阶段，支持向量机模拟超声参数与应力关系的误差较大，预测结果一般高于真实值模型偏安全。简单支持向量机模拟效果较差，在低应力阶段尤为明显，用遍历算法得到的参数进行支持向量机模拟的效果较优，但计算时间过长；采用粒子群算法进行参数优化，能够大幅度缩短计算时间，模拟效果最优，更具有应用价值。