Hopkinson杆式冲击疲劳试验方法研究

李泊立， 赵思晗， 刘圆梦， 杨建辉， 郭伟国

(西北工业大学 航空学院，西安 710072)

近年来，装备和结构使用新材料以及轻量化等越来越突出，使得确保装备与结构具有高可靠性非常关键。对于经受反复高过载冲击的结构，例如飞机起落架的冲击着陆、舰载拦阻钩的高速撞击、钻井泵阀的冲击疲劳问题[1]等。装备结构的材料本身存在空位、晶界等微观组织缺陷，而焊接、复合材料三维编织和增材制造等工艺会引起各种工艺缺陷，比如增材制造材料存在气孔、未熔合等缺陷[2]，如图1(a)所示。当这类材料在低于材料弹性比例极限(一些条件下也可能高于材料弹性比例极限)的载荷的重复作用下，缺陷累积至形成裂纹到最后破坏，这是疲劳研究的重点。一方面疲劳载荷的加载率(应变率)往往在每秒数十兆帕(振动疲劳加载速度通常小于20 mm/s)，为了提高加载应力率，就需要提高加载速度，而分离式霍普金森压杆(split-hopkinson press bar, SHPB)加载速度可达30 m/s；另一方面尽管对试样的加载应力是在弹性比例极限以下，如图1(b)所示，在三点弯曲试样宏观裂纹尖端，材料局部应力进入到塑性范围，当加载速度提高，此区域的材料应变率会超过104s-1，出现明显的塑性区，如图1(c)所示。这样在高应力率或高速疲劳加载，即冲击疲劳试验下揭示材料疲劳损伤与扩展机制并给出寿命特性就变得很有工程和理论意义。

图1 疲劳试验中缺陷的影响Fig.1 The effect of defects in fatigue test

冲击疲劳相对于常规疲劳，在于加载情况不同，二者虽都是循环载荷，但单次冲击加载波形之间有着不同时间的间歇，冲击加载往往是从零载到压或拉的单向连续冲击，冲击速度快、加载速率高、作用时间短，且要考虑冲击载荷产生的应力应变在结构或材料内部的应力波形式传播，另外材料中的应力应变不均匀性要比常规疲劳载荷下的大[3]。冲击疲劳相对于单次大能量冲击破断，冲击疲劳实际上是材料或构件在小能量多次冲击条件下发生的疲劳失效行为[4]，存在损伤累积过程。

对冲击疲劳的研究最早可追溯至1908年Stanton等[5]对碳钢进行的多次重复冲击弯曲试验，提出多次冲击试验可以判断材料的冲击断裂抗力如何。国内较早进行冲击疲劳研究的周惠久等[6]，研究了钢不同成分、回火温度和缺口对冲击疲劳性能的影响，认为多次冲击抗力不单纯取决于材料的强度因素，同时一定程度上取决于材料的塑性特性。另外一些学者[7-9]对材料的连续多次冲击试验表明，冲击下疲劳强度低于非冲击(常规)疲劳，冲击疲劳的裂纹扩展速率高于非冲击疲劳；热处理工艺和材料微观组织对冲击疲劳性能的影响十分显著。

另外，在试验方法或技术层面，由于冲击疲劳缺少统一的规范标准以及先进的试验装置，使得冲击疲劳问题的研究难度大。现有的冲击疲劳试验装置大致可分为两类：①依靠落锤质量自由下落的冲击形式[10-11]，在试验过程中可通过改变落锤质量和高度实现不同能量的冲击，冲击频率一般小于1 Hz；②通过电机旋转带动冲击头的连续冲击形式。这类机构的特点是采用电机带动机械结构运动，如利用凸轮旋转带动摆锤对试样进行循环冲击[12]，冲击频率大约为1.43 Hz，冲击能量为0.6 J；利用曲柄连杆机构将旋转运动转化为平移运动来获得循环冲击力[13]，冲击能量在3～7 J；利用凸轮-弹簧式加载机构实现反复冲击[14]，试验机采用卧式布置，通过电机转速、弹簧刚度和预压量与控制系统调节冲击频率、冲击冲量和冲击次数，电机转速在100～1 000 r/min内，冲击力在2～10 kN内。这些基于能量法冲击疲劳技术，在冲击波构形显示、冲击加载率和冲击波波形控制等方面有不足之处。

对此，本文基于SHPB原理，通过气压控制撞击杆速度来改变冲击能量，利用入射和透射杆上的应变采集来显示冲击波形，改变撞击杆的几何构形来控制冲击波波形，最终实现对试样的Hopkinson杆式冲击疲劳加载与数据采集显示。通过对高强度钢圆柱试样进行测试试验，表明该方法可实现加载频率在0～0.5 Hz，加载率能达到3×106MPa/s。最后通过增材制造316 L不锈钢三点弯曲试样验证了利用该方法在研究冲击疲劳问题中的适用性。

1 Hopkinson杆式冲击疲劳装置原理

1.1 不同冲击循环速度的实现

如图2所示，为了实现撞击弹(常称撞击杆)的不同的高速冲击，以及循环撞击，采用高压空气或氮气驱动方式，其撞击弹发射原理可参考文献[15]，进气电磁阀在综合控制器操控下打开，空压机向气室充入气体，当气室压力到达预定值，启动高速发射阀，撞击弹沿炮管撞击入射杆，入射杆上贴有应变计记录冲击波信号。这时在综合控制器控制下自动关闭进气电磁阀，再打开真空器的出气电磁阀把撞击弹沿炮管吸回到炮管底部预定位置，接下来再重复发射。

图2 撞击弹循环撞击原理图Fig.2 Schematic of cyclic impact of projectile

不同冲击能量的控制，即撞击弹的发射速度控制，由发射时气室中的气体压力决定。在撞击弹发射过程中，由于撞击弹后端炮管容积增加，气体压强在一定程度上会减小，因此使发射撞击弹的储气室容积大于5倍炮管内容积，则撞击弹在炮管加速度的驱动压力变化可以忽略，撞击弹在炮管中的运动可视为在恒压下的恒加速度运动，于是撞击弹的运动过程可用牛顿运动方程表示

(1)

式中:v，a和m分别为撞击杆的速度、加速度和质量；P0为高压气室的初始气压；S为炮管内径面积。整理方程两边可得微分方程

(2)

对式(2)两边积分中即可得到撞击弹在炮管出口速度的表达式

(3)

式中，L和l分别为炮管和撞击弹长度。考虑到磨擦、漏气等影响，气压内能转化为撞击弹动能的过程中存在能量转换效率的问题，用η来表示，则转换效率一般介于85%～95%。

(4)

根据式(4)，对于质量m=0.45 kg，长度l=200 mm的撞击弹和内径φ=30 mm，长度L=1 600 mm的炮管，不同气压下的撞击弹出口速度如图3所示(高压气室选择SC125×400标准气缸)。

依据Hopkinson压杆原理，在入射杆中部粘贴高精度应变计，通过高压发射-真空吸弹-再高压发射循环发射撞击弹， 在入射杆获得的典型连续冲击波形如图4所示。表1给出了图4中每次冲击后应变计所测第一个入射波与反射波的幅值与相邻两次冲击的时间间隔，并计算得出相对误差。可知在气室容积较大和压力稳定情况下，连续冲击的幅值误差小于5%，连续冲击机构工作可靠。

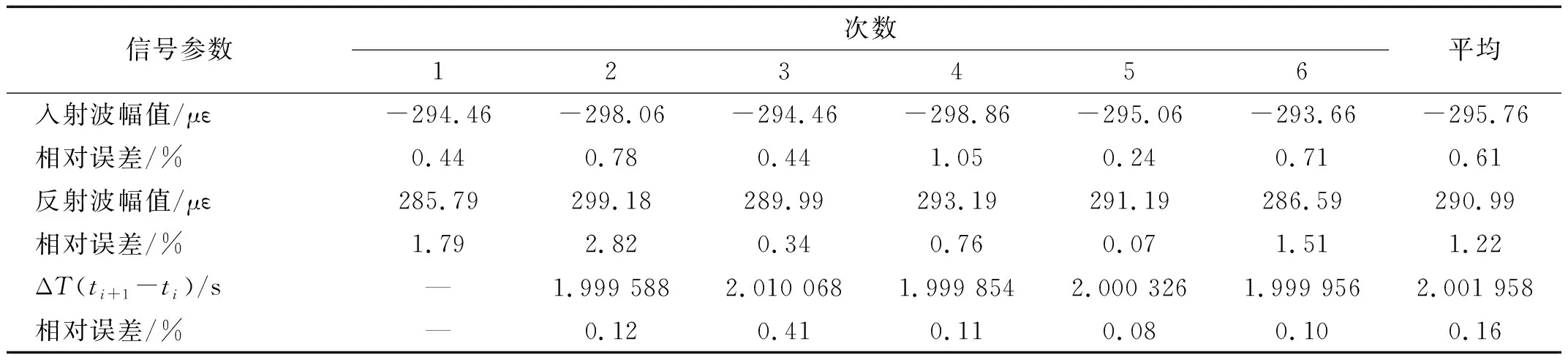
表1 入射杆信号的周期及幅值相对误差Tab.1 The relative error of cycle and amplitude of the signals on the incident bar

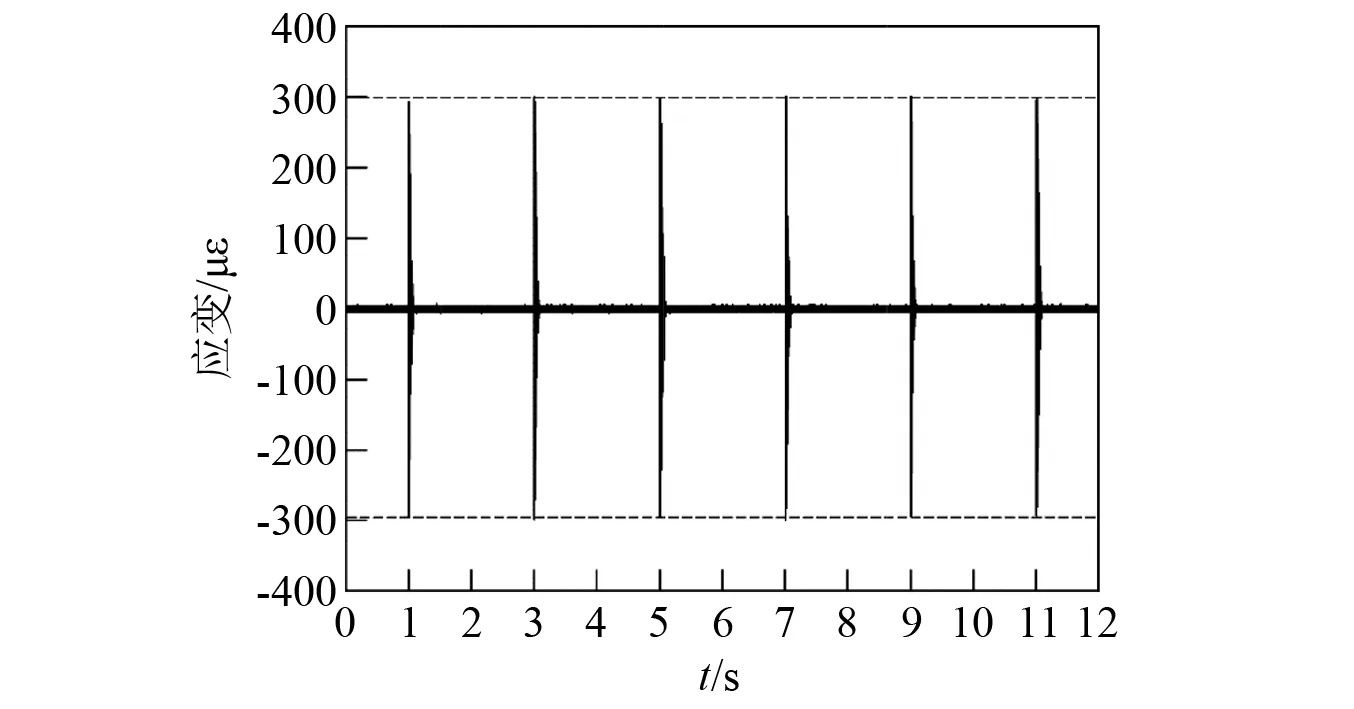
图4 在入射杆获得的循环冲击信号Fig.4 Continuous signals of cyclic impact on the incident bar

1.2 不同冲击波构形的实现原理

根据一维应力波的基本理论和Hopkinson杆原理，对于图5所示撞击弹撞击入射杆时，在入射杆端的速度为

(5)

式中：C为入射杆一维纵向波速；ρ为杆的密度;ε(t)和σ(t)分别为杆上的弹性应变和应力历程。如果入射杆和撞击弹是相同的直径和材料，入射杆上的应力和撞击弹撞击速度v1(t)有如下关系

(6)

如果撞击弹是几何复杂的构形，例如是纺锤形，其截面面积为φ1(x)，入射杆截面面积为φ2，则在入射杆上产生的应力波形近似为

(7)

式中：ρ1,C1为撞击弹的密度和波速；ρ2,C2为入射杆的密度和波速。异形撞击弹撞击产生的冲击脉冲构形如图5所示。由于撞击弹与入射杆撞击后，应力波在异形撞击弹中传播比较复杂，不容易获得解析解，借助试验测试，图6给出了模拟计算出的5种撞击弹以10 m/s的撞击速度撞击直径为19 mm的入射杆所产生的冲击波形，说明在入射杆上产生的冲击应力波或应变波脉冲基本构形与的撞击弹的几何构形、密度以及速度有关。这样通过改变撞击弹的密度和几何构形，各种所需要的波形基本可以获得[16]。

图5 撞击弹产生应力波脉冲示意图Fig.5 Schematic diagram of the stress wave pulse produced by a projectile

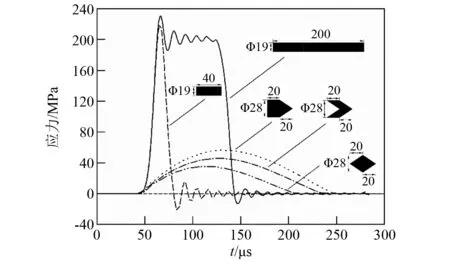
图6 不同撞击弹产生的冲击波形Fig.6 Impact waveforms produced by different types of projectiles

另一方面，当发射气压恒定时，冲击力波形的宽度也由撞击杆的长度决定，冲量的重复精度误差小于2%。

1.3 不同冲击频率的实现原理

在冲击疲劳试验中，对冲击频率的控制也是值得关注的。见图2，由于本试验系统通过二通电磁阀开/关控制驱动气压压力值以及撞击弹发射，撞击弹发射和回收是程控自动实现，因此电磁阀时序控制周期影响了系统的冲击循环周期。

(8)

式中，T1，T2和T3分别为三个电磁阀的工作循环周期。综合控制器控制三个常闭电磁阀进行如图7所示工作循环。图7中：ti1和ti2分别为电磁阀通、断的时间；Ti为电磁阀的工作周期；电磁阀1连接真空气室与炮管，电磁阀通则炮管与真空气室连通，撞击杆受炮管内外压力作用运动复位到炮管底部预定位置；电磁阀2连接空压机与气室，电磁阀通则高压气体进入气室，通过改变时间t21可调整每次发射的气压，进而控制撞击杆撞击速度；电磁阀3作为高速发射阀，通电即可使撞击弹快速发射。另外，为保证每次循环的时间保持一致，需保证T1=T2=T3。因此，在第一次循环开始前依序设置延时，保证三个电磁阀依序完成第一个工作循环后再进行后续循环；另一方面，还增加了一个电动推杆与控制电磁阀的控制器相连，当电磁阀工作循环结束以后，控制器输出电信号使电动推杆推动透射杆回到原位。

图7 电磁阀工作循环示意图Fig.7 Schematic diagram of cyclic working of solenoid valves

通过综合控制器控制电磁阀工作循环的时间，进而实现恒定的“吸弹-充气-发射”工作周期，也就表现为稳定的冲击频率。电动推杆的最大推进频率为0.75 Hz，考虑到其本身的频率范围和推动速度对试样的力学响应，则可改变综合控制器的控制程序实现低频(0)～高频(0.5 Hz)的冲击频率控制。

2 冲击疲劳验证试验

在西北工业大学现有的SHPB装置上进行了改进[17]，如图8所示，在发射炮管设置连接了一个真空泵系统，以实现撞击弹在炮管中的回吸复位功能，通过程序综合控制控制实现自动化重复冲击。在入射杆上增加质量轻、弹性好的弹性限位装置，使入射杆在每次受到撞击杆撞击后能自动回到原位，并且该装置不会对应力波在杆中的传播产生影响。通过增加电驱动自动回位装置，使透射杆受到撞击弹开后，靠电动推杆推动其回到原位，由此可以进行新一次加载，这种方法可以方便地对试样进行冲击疲劳加载；另一方面，该装置的设计需要考虑到装置本身的寿命情况，在预先设定试样的循环载荷时，需要保证加载杆上的载荷不高于杆材料的抗拉强度的30%，在这样的循环应力下即可认为杆是无限寿命的。论文首先选择了高强钢圆柱试样对该方法进行测试，再使用增材制造316L不锈钢三点弯曲试样通过该方法进行冲击疲劳试验，证明这种方法的适用性。

2.1 圆柱试样循环冲击结果

通过对高强度钢圆柱试样(Φ10×9 mm)进行循环冲击，撞击杆、入射杆和透射杆的材料为18NiC350高强钢。为了防止试样在受到冲击后掉落，设计了如图8(a)所示的圆柱试样固定滑套，滑套两端的内径与加载杆直径相同，滑套中部内径略大于试样直径，并与试样之间用一层软橡胶圈包裹，防止试样受围压作用。并在入射杆和透射杆中部粘贴高精度应变片得出循环冲击的信号，如图9所示。对其中一次冲击的部分信号放大，如图10所示，是典型的SHPB加载波形。为了实现低应力多次冲击，在弹性范围内对试样进行加载，所得到的每次的应力应变曲线如图11所示。根据SHPB原理，若试样两边受力平衡，则入射波与反射波的叠加等于透射波，入射波加反射波实际为试样的加载波。因此通过不同形状的撞击杆对试样进行加载，可以得出不同加载率的加载波，如图12所示。等截面圆柱撞击弹的加载率最大，为2.98×106MPa/s，变截面撞击弹使用了两种，其加载率分别为1.43×106MPa/s和0.78×106MPa/s。

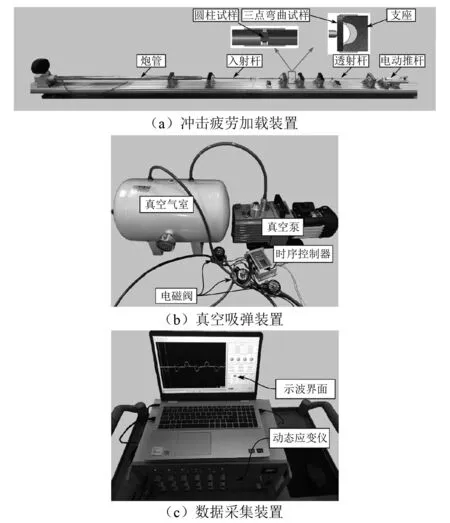
图8 冲击疲劳试验装置照片Fig.8 Photographs of impact fatigue experiment

图9 应变仪采集的连续信号Fig.9 Continuous signals acquired by the strain gauge

图10 单次冲击时的部分波形Fig.10 Part of the waveform at a single impact

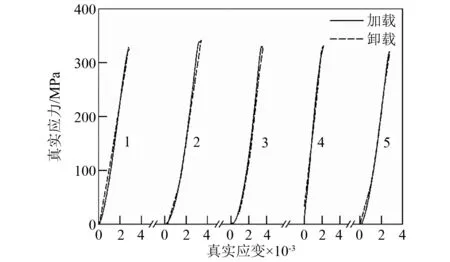
图11 弹性范围内多次冲击的应力应变曲线Fig.11 Stress-strain curves of multiple impacts in the elastic range

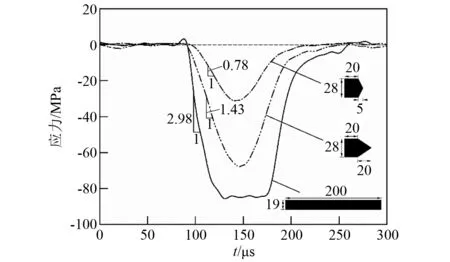
图12 三种撞击杆产生的不同加载率的加载波Fig.12 Loading waves with different loading rates produced by three types of projectiles

2.2 三点弯曲试样循环冲击结果

选用增材制造316L不锈钢材料制备加工三点弯曲试样(4 mm×8 mm×50 mm)，试样中间利用线切割预制深度为2.5 mm的裂纹。为了更好地符合三点弯曲试样的受力状况，将入射杆端头加工成半圆弧状与试样接触，并需制作相适应的支座与透射杆通过螺纹紧密连接。对于三点弯曲试样，同样设计了一个如图8(a)所示的夹具来固定试样，该夹具可以限制试样的横向位移，防止试样在受到小能量冲击时脱离支座。撞击杆、入射杆和透射杆的材料由表2给出。按照这种方式进行加载，三点弯曲试样受力简化为如图13所示，假设试样受力平衡，即

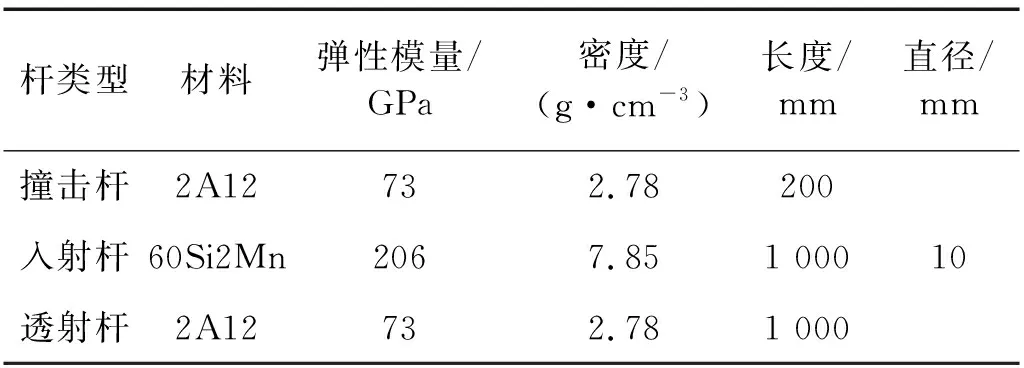
表2 撞击杆、入射杆和透射杆材料及尺寸Tab.2 Material and geometries of projectile, incident bar and transmission bar

图13 三点弯曲试样受力简化图Fig.13 Force analytical diagram of three-point-bending specimen

F1(t)=2F2(t)

(9)

根据纯弯曲梁弯曲横截面上正应力计算公式

(10)

式中：M为弯矩；y为横截面上距离中性层的距离；Iz为横截面的惯性矩。因此三点弯曲裂纹尖端的弯曲正应力表达式为

(11)

对增材制造316L不锈钢三点弯曲试样进行了冲击疲劳试验，三点弯曲试样在冲击力大小为1 kN，加载速率为1.1×106MPa/s，冲击频率为0.5 Hz的冲击疲劳试验下，受到462次循环冲击后彻底断裂。三点弯曲试样分别在冲击疲劳载荷下和单次大能量冲击载荷下断裂后的断面放大图，如图14所示。图14(a)可以将断面分为线切割区、裂纹萌生区、裂纹扩展区以及瞬断区。试样在冲击疲劳载荷作用下，线切割边界处应力集中，裂纹在线切割区边界多点同时萌生，萌生区的断面不平整，存在挤出峰和挤入槽。在裂纹扩展区有一明显的垂直于裂纹扩展方向的弧形亮带，断面较为平整。最终试样在过载情况下瞬间破断，这与图14(b)的断裂模式类似，由于是在过载情况下断裂，断面较为平整，裂纹扩展方向有明显的放射状条纹。

图14 三点弯曲试样断口显微图像Fig.14 Microscope image of the fracture surface of 3PB specimen

3 结 论

本文提出了一种基于分离式霍普金森杆技术的冲击疲劳试验方法。基于对传统Hopkinson压杆试验装置的改进，实现了快速自动化重新复位和加载的能力。通过对高强度钢圆柱试样进行测试，该装置能够实现对试样在频率0～0.5 Hz内的循环冲击加载，可通过控制撞击弹速度改变加载幅值，控制撞击弹几何形状实现不同加载波形(梯形波、三角波或半正弦波)和加载率(8×105～3×106MPa/s)，并能准确测量试样的力学响应。通过对增材制造316L不锈钢的三点弯曲试样进行冲击疲劳试验，验证了该方法在冲击疲劳研究中的适用性。