板桩支挡结构的应力与位移弹性理论解

付小蝶，张爱军，王彬铧，刘宏泰

（1.西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100；2.机械工业勘察设计研究院有限公司，陕西 西安 710043）

1 研究背景

板桩支挡结构是为防止土体坍塌而修筑且主要承受侧向土压力的结构，被广泛应用于支撑路基填土、基坑坑壁或路堑边坡，以及河流堤岸与桥台隧道洞口等支护工程中[1-2]。近年来，我国各类支护工程发展迅猛，支护工程的安全问题[3-4]被日益重视，而进行支护工程设计的关键在于计算结构的应力和位移。目前，板桩应力和位移计算的方法有数值计算[5-6]和解析计算[7-8]两类。Liu等[9]采用现场监测和有限元数值模拟相结合的方法，分析并验证板桩支挡结构的应力变形规律；Yuan等[10]结合理论分析、现场检测和M IDAS GTS NX数值模拟，研究了板桩支挡结构变形规律，进行板桩设计与分析；Zhang等[11]基于三维建模平台 ITASCAD进行板桩支护分析，实现支护结构设计及支护变形可视化。传统的三维有限元数值模拟法虽然可以考虑复杂的边界条件与荷载变化，但是它需要专业的模拟软件、繁杂的计算工作以及大量的实测数据，因此三维数值模拟法更适用于最终设计方案的细节处理，并不适用作为一个初步的常规设计工具。孙训方等[12]采用解析公式法将板桩视为悬臂梁，计算板桩σx和τxy的分布和解析式，但没有给出板桩位移的计算式，也无法计算σy和板桩上任一点的应力分布，不够全面和准确。

土压力是支护工程中板桩所需要承受的主要荷载[13]，板桩土压力的理论计算有：1773年法国学者Coulomb提出了抗剪强度理论公式以及利用楔形体平衡法计算板桩上的土压力；1869年英国学者Rankine提出了主动及被动状态下土压力理论；目前大多直接采用两类经典土压力理论进行主动或被动极限状态下的土压力和板桩应力分布的计算，但实际工程中板桩位移大多达不到极限状态[14-15]时所需要产生的位移，此时经典土压力理论则不再适用，为此众多学者开展了关于土压力变化与板桩侧向位移关系的研究。张常光等[16]对随板桩侧向位移的非线性变化土压力的数学拟合法进行了总结与分类，如喻军等[17]认为离开土体移动的板桩所受土压力通常介于静止土压力与主动土压力之间，其采用三角函数拟合土压力和位移曲线，考虑随支护结构位移非线性变化的土压力；胡志平等[18]在主动极限状态下将土压力-位移曲线拟合为双曲线，分析土压力与板桩侧向位移的非线性关系。蒋鹏等[19]表示产生远离土体板桩位移的板桩所受土压力大于朗肯主动土压力，并认为其存在非线性关系，基于支护结构位移对土压力影响的计算分析，利用二次函数拟合土压力-位移曲线。此外，王正振等[20]认为随板桩侧向位移的产生，作用于板桩的土压力是非极限土压力已不再适用于传统朗肯理论，基于朗肯土压力理论借鉴双参数法，结合地下结构弯曲微分方程进行受位移影响的土压力非线性计算；党发宁等[21]认为实际工程建设中，板桩产生的侧向位移是有限的，很难达到极限平衡状态，此时板桩所受土压力也非极限土压力，基于弹性理论利用应变推导有限位移条件下土压力-位移公式。目前，众多学者研究表明：随板桩产生离开土体的侧向位移增大，作用于板桩的土压力也由静止土压力过渡到非极限土压力，直至趋近朗肯极限土压力。因此，板桩应力和位移计算中直接采用朗肯主动土压力是不合理的，应该考虑板桩侧向位移对土压力的影响。

本文基于弹性理论，建立了板桩应力及位移分布计算模型，结合边界条件与相容方程，采用半逆解法得出了极限平衡条件下板桩应力及位移分量解析解。同时，在党发宁等[21]研究的基础上，以悬臂板桩支挡结构为例，考虑土压力随板桩侧向位移非线性变化，假定板桩产生绕墙角的转动位移（RB位移模式），引入有限位移条件下土压力-位移效应公式，修正板桩应力及位移解析计算式，得出了有限位移条件下板桩应力及位移分量解析解。同时，利用ADINA建立板桩支挡结构的二维模型，计算得出基坑支护工程中板桩支挡结构应力及位移的数值解，通过对比解析解和数值解，验证了本文解析计算公式的合理性。

2 板桩支挡结构计算模型的建立与求解

2.1 计算模型的建立与基本假定以水平方向为y轴，竖直方向为x轴，建立板桩支挡结构几何计算模型，如图1所示。

图1 板桩应力及位移分布计算模型

图1中ρg为土体重度，φ为土体内摩擦角，ρ1g为板桩的重度，h为基坑的深度，l为板桩高度，b为板桩宽度，E0为静止土压力，Ea为主动土压力。

本文基本假定如下：（1）板桩绕桩底产生转动位移；（2）满足平面应变问题；（3）基坑开挖面以下视为固定端，不计土的刚度；（4）满足材料连续性与各向同性假定；（5）位移和形变是微小的。

2.2 计算模型的求解由朗肯土压力理论得：

式中：Ka为主动土压力系数；Ea为主动土压力，kPa；K0为静止土压力系数；E0为静止土压力，kPa。

基于假定（4），考虑板桩平衡条件，引入二维Navier方程：

式中：fx为x方向的体力分量；fy为y方向的体力分量，其中fy=0，fx=ρ1g。

对常体力情况下的Navier方程进行简化，得出该方程全解：

式中Φ为艾里应力函数。

采用半逆解法，利用板桩左右两面上水平应力是x的一次函数的事实，假定σy=xf（y），若满足所有的边界条件则假定的函数是正确的解。

为推求艾里应力函数Φ的形式，将σy代入式（4）有：

对式（5）中y积分，得：

式中：f（y），f1（y）和 f2（y）均为待定的函数。

上式为关于x的一元三次方程，由于相容方程要求全板桩内的值都满足式（7），即要求方程有无穷多个根，则方程各项系数和自由项均为零，即：

对上式中 f（y），f1（y）和 f2（y）分别进行积分，确定 f（y），f1（y）和 f2（y）为关于的多项式，将其代入式（6）确定应力函数Φ形式，得：

式中A、B、C、D、E、F、G、H、I均为待定系数。

将式（9）代入式（4），得应力分量：

上述应力分量均满足相容方程和Navier方程，若选择系数A～I满足所有边界条件，则式（10）中应力分量即为模型的正确解答。

由于板桩的高度远大于板桩的宽度，板桩的左右边界为全部边界的绝大部分，因此板桩左右两个边界为主要边界，在主要边界上应力边界必须完全满足，得：

式中：Ea为朗肯主动土压力，kPa；S为土压力在板桩一侧的作用宽度，m，这里取单位宽度，即S=1 m。

板桩上下两个边界为次要边界，由于次要边界上边界条件无法完全满足，因此引用圣维南原理，采用积分的边界条件近似代替，得：

结合式（10），联立式（11）、式（12）可求解A～I全部待定系数，整理后得式（10）土的极限平衡状态下板桩应力分量解析式：

式中：Ix为对x轴的惯性矩，m4，Ix=b3h/12；Iy为对y轴的惯性矩，m4，Iy=bh3/12。

由假定（5），并结合弹性力学几何方程和物理方程推求应变、应力与位移的关系，得：

阿姆斯特丹有160多条大小运河，1000多座风格迥异的古老的桥梁。运河两边有许多贵族宅邸，也是阿姆斯特丹特有的风景之一，它们将运河和桥梁烘托得极其典雅。这些曾经是17世纪荷兰富商居住的房屋，至今仍然保持着古老的浮华。在这些豪宅里，飘荡着荷兰文化杰出的代表林布兰和梵·高的艺术灵魂，也隐藏着二次大战中犹太女孩安妮和她的《安妮日记》这样的悲惨故事。每年6月郁金香盛开的季节，从花市集散地驶来的满载鲜花的几百艘船只浩浩荡荡地穿行在运河上，一下子成了花的河，花的街。

式中：E为弹性模量，MPa；μ为泊松比；ux为板桩竖向位移，m；uy为板桩水平位移，m；εy为板桩的水平应变；εx为板桩的竖直应变。

将基坑底部开挖面以下视为固定端，即假定开挖面以下板桩位移为零，确定位移边界条件，得：

对式（14）中ux及uy进行积分，并将积分结果代入式（15），求解位移分量中的待定系数，得：

考虑到本模型中板桩位移应按平面应变问题处理，因此需将E、μ从平面应力参数转化为平面应变参数：

利用参数转化，将式（17）代入式（16），可得土的极限平衡状态下板桩位移分量解析式：

将式（13）与式（17）代入式（14），可得板桩水平应变εy分布如下：

结合式（2）与式（19），计算得出板桩水平应变的最大值εymax如下：

2.3 有限位移条件下板桩应力及位移的修正以上推导过程中设定板后土压力按照朗肯公式计算得出，计算所得结果为极限平衡状态下的土压力。实际上，板后土压力不仅受到土体性质、板桩高度以及板桩刚度等因素影响，而且与板桩本身的位移也密切相关。从实际工况来看，板桩产生的离开土体和靠近土体的位移偏移量有限，很少达到极限平衡状态，采用朗肯公式计算的主动土压力和被动土压力均偏大，相应条件下计算出的板桩的应力和位移也偏大，需要修正，因此将朗肯主动土压力修正为有限位移条件下的土压力：

式中：P*为有限位移条件下的土压力，kPa。

文献[21]将板后土体未达到极限状态而板桩产生绕桩底的转动位移定义为RB位移模式，得到在RB位移模式下土压力P*与板桩水平位移uy存在非线性关系，且与板桩水平应变εy存在以下关系：

将式（22）代入式（13）与式（18）中，得土压力-RB位移模式下应力分量最终形式：

土压力-RB位移模式下位移分量最终形式：

值得注意的是，本文在进行板桩应力与位移解析式推导的过程中，并没有完全假定开挖面以下为固定端，笔者先假定其为固定端，再引用文献[21]中的成果对应力与位移的解析式进行修正，修正后的结果式（23）、式（24）是考虑了开挖面以下板桩位移的，而不是再将开挖面以下视为固定端。

3 土压力-RB位移模式下板桩应力及位移解析式验证

3.1 实例验证与ADINA数值分析采用许雷挺等[22]模型试验所用砂土试样，作为板后填土，确定有限位移条件下板桩应力与位移计算试验参数。表1所示为板桩计算参数，表2所示为土体计算参数。

表1 板桩计算参数

表2 土体计算参数

结合式（1）与式（2）可计算出板桩极限平衡条件下的朗肯主动土压力、静止土压力和对应土压力系数，由式（23）知，εymax的解析式为关于x的单调函数，因此当x=h时计算可以得出文中板桩支挡结构所对应的水平应变最大值。表3所示为极限状态下土体的计算参数。

表3 极限状态下土体计算参数

为验证文中板桩应力及位移解析解的正确性，计算板桩应力及位移的数值解进行对比验证。通过图1与ADINA有限元软件建立基坑及板桩支挡结构的二维数值计算模型，模型以水平方向为y轴，竖直方向为x轴，板桩与土体刚度差异过大，在二者间设置接触组与接触单元。

图2所示为有限元分析计算的模型与网格划分，表4所示为有限元分析计算的模型所用材料参数与单元类型。

图2 ADINA数值计算模型

表4 ADINA计算中材料模型与单元类型

3.2 土压力-RB位移模式下板桩水平位移分布由式（18）、式（21）与ADINA计算得出，极限位移条件下（即土体产生极限位移的极限平衡条件）、土压力-RB位移模式下与ADINA数值计算下板桩水平位移分布uy，uy分布曲线如图3所示。

图3 三种计算模式下板桩水平位移分布图

由图3可以看出，三种计算方式所得水平位移均符合板桩发生绕桩底转动的假定与小变形假定，三者位移曲线沿桩高呈非线性分布。极限位移条件下计算曲线与土压力-RB位移模式下计算曲线均严格表现为三次曲线形，其位移分量的分布与ADINA数值计算值趋势基本一致。极限位移状态下计算没有考虑土压力随板桩位移的变化，其土压力为极限土压力，即是土压力的最大值，而实际情况中，板桩水平位移很难达到极限条件下的极限位移，因此极限条件下的计算结果比实际情况偏大，并不准确。而土压力-RB位移模式计算结果由于考虑土压力随板桩水平位移的变化，与极限条件下计算结果相比偏小，更加符合实际工程，其位移曲线更贴近真实情况。

3.3 土压力-RB位移模式下板桩竖向位移分布由式（18）、式（21）与ADINA计算得出，极限位移条件下、土压力-RB位移模式下与数值计算下板桩竖向位移 ux分布，ux分布曲线如图4所示。

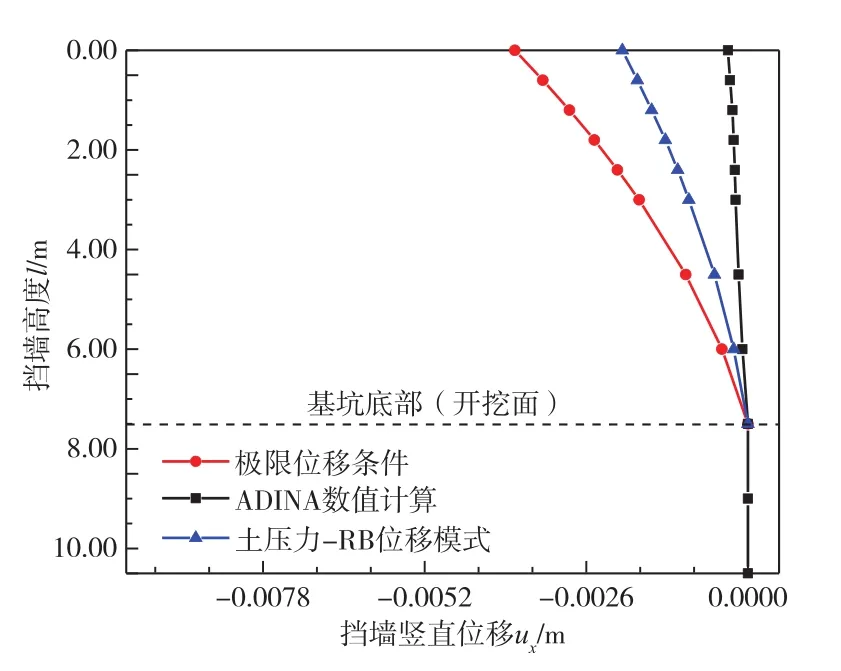
图4 三种计算模式下板桩竖直位移分布图

由图4可以看出三者位移曲线沿桩高呈非线性分布，极限位移条件下计算曲线与土压力-RB位移模式下计算曲线严格表现为二次曲线形，ADINA数值计算其线形弯曲程度受材料参数影响较大，其趋势表现为单调递减。参照 《建筑基坑支护技术规程规范》（JGJ120—2012）[23]对板桩位移进行分析，10.5 m高板桩产生0.5 cm竖向位移，符合规范对于基坑支护中板桩竖向位移安全性的要求。综合看来，极限位移条件下与土压力-RB位移模式下的竖向位移曲线与数值计算结果基本吻合，且土压力-RB位移模式下位移曲线为严格二次形曲线，与数值计算结果吻合程度更高，用以分析板桩水平位移的效果更好。

3.4 土压力-RB位移模式下板桩应力分布由式（18）、式（21）与ADINA计算得出，极限位移条件下、土压力-RB位移模式下与数值计算下板桩水平应力σy与竖直应力σx分布。σy分布曲线如图5所示，σx分布曲线如6所示。

图5 三种计算模式下板桩水平应力分布图

图6 三种计算模式下板桩竖直应力分布图

由图5、图6对比分析可以看出，极限位移条件下计算曲线与土压力-RB位移模式下计算曲线曲线沿桩高呈线性分布，符合材料力学中悬臂梁应力分布，同时满足极限状态的土压力小于有限位移状态土压力的要求。ADINA数值计算应力曲线沿桩高近似线性分布，近似单调递增。需要注意的是，有限元数值计算中板桩底部会出现应力集中的情况，无法有效对板桩底部的应力分布作有效分析，因此采用极限位移条件计算和土压力-RB位移模式计算可以较好规避这一问题。此外，运用土压力-RB位移模式下的计算公式在处理板桩应力及位移问题时，由于考虑了土压力随板桩侧向位移的非线性变化，其水平与竖向应力变化与数值计算吻合程度更高，更加符合实际情况。

3.5 土压力-RB位移模式下应力及位移结果讨论本文推导的计算公式较简单地将板桩当做悬臂梁来计算的传统方法有较大的进步。传统悬臂梁计算公式与本文推导的解析公式推导均假定开挖面以下为固定端，不计板桩位移，但本文公式进行修正后考虑板桩位移效应的影响，比之更为合理。且悬臂梁应力计算公式由于采用了平截面等假定无法计算σy，且无法考虑板桩位移的影响，对其他应力分量以及位移的计算精度也不足，而本文推导的理论公式不但给出σy和位移分量的解析计算式，还可以求取板桩任一坐标点的应力及位移分布，能够更好的分析板桩变形，这是本文理论公式的优势之一。

此外，本文公式考虑了土压力随板桩侧向位移呈非线性变化的关系，以土压力-位移效应修正了理论计算公式，区分极限位移状态和有限位移状态，更贴合实际情况，这是本理论公式的优势之二。

由于本文忽略了土体的刚度，文中理论公式只适用于板桩刚度与土体刚度相差较大的支护计算，比如：钢板桩、或者软土地区混凝土板桩支挡结构等；同时本文将板桩底部开挖面视为固定端，虽然经过修正后考虑了开挖面以下板桩的位移，但是忽略了开挖面以下板桩两侧的土压力影响。因此，推导考虑土体刚度和开挖面以下板桩两侧土压力影响的解析计算公式是笔者下一步的研究工作。

4 结论

本文针对支护工程中板桩支挡结构的应力和位移计算问题，基于弹性理论，考虑了土压力与板桩侧向位移的非线性关系，区分极限位移状态和有限位移状态（RB位移模式），建立了有限位移条件下板桩应力分量和位移分量理论计算公式；采用ADINA分析软件建立板桩支挡结构数值模型，对比分析极限位移条件下解析解、土压力-RB位移下模式解析解和ADINA数值解，验证了本文提出的板桩应力与位移理论计算公式的正确性与适用性，得出以下结论：

（1）依据弹性理论及基本假定，建立了板桩应力与位移分布理论计算模型，结合边界条件与相容方程，采用半逆解法推导出了极限位移条件下板桩应力与位移分量解析计算公式。

（2）根据文献[21]引入有限位移条件下土压力计算公式，考虑土压力与板桩侧向位移的非线性关系，修正完善土压力-RB位移模式下板桩应力与位移解析计算公式，并采用数值计算验证，两者符合较好。

（3）提出的解析计算公式较将板桩简单当做悬臂梁计算更为精确可靠，较数值计算更为简单便捷，可作为板桩支挡结构常规设计的工具，具有重要的实用价值。