基于信号时频特征的微震波形识别在岩爆预测中的应用
李文旭,陈祖煜,,唐春安,苏 岩,唐烈先,胡 晶,陶 磊
(1.西安理工大学 省部共建西北旱区生态水利国家重点实验室,陕西 西安 710048;2.中国水利水电科学研究院,北京 100048;3.大连理工大学 土木工程学院,辽宁 大连 116024;4.陕西省引汉济渭工程建设有限公司,陕西 西安 710010;5.辽宁科技大学 矿业学院,辽宁 鞍山 114051)
1 研究背景
岩爆通常具有瞬时性、猛烈性,在发生岩爆时,大量的岩块和碎石以高速弹射出围岩,严重威胁施工人员及设备的安全。因此,深埋隧道围岩的岩爆灾害监测预警成为亟待解决的重大课题[1]。
现阶段,通过微震监测来预测岩爆的手段现已趋于成熟,在矿山、隧洞、地下厂房等工程领域得到了广泛的应用[2-3]。然而在施工过程中,微震监测系统需要实时采集数据,工程师每天需要处理数万条波形,而采集的数据中90%为噪声、机械振动等无效信号,对岩爆预测并无帮助,例如在引汉济渭工程中自桩号K33+870~K47+150之间,微震监测团队总共检测到478 874条地震波信息,其中只有61 796条为微震信息,研究人员再从6万余条微震信息中通过经验和神经网络学习以及综合分析中分析实际产生岩爆的事件,显然从47万余条地震波中,把与微震无关的信息剔除,其工作量十分巨大,监测的效果在很大程度上取决于研究人员相关的技术水平。如何在大量的信号中快速、准确识别出岩石微破裂产生的微震/岩爆信号是提高岩爆预测效率的关键问题之一。Malovichk等[4]利用微震事件的辐射模式、能量分布以及不同波形的相关性等特征,采用最大似然法对矿山的正常事件和微震事件进行了分类;Ma等[5]对震源参数和波形参数进行特征提取,建立了基于贝叶斯判别法的波形识别模型,在识别爆破和微震事件中可以达到97.1%的准确率,并且在Yongshaba矿山中得到了很好的应用;Dong等[6]提取了地震记录起始时间、地震力矩、总辐射能量和静态应力降等参数的概率密度函数,研究了Fisher分类器、朴素贝叶斯分类器和logistic回归在地震事件和爆炸事件识别中的适用性和性能;陆菜平等[7]基于傅里叶变换对微震信号的主频段和幅频特性进行分析,为微震信号分析提供了一个新的角度。然而,目前很难通过简单的信号处理剔除数据中的无效数据,需要工程师凭借经验进行筛选,具有一定的主观性。
采用人工智能对大数据进行训练学习,可以解决这一局限,提高微震识别的效率和可靠性。朱权洁等[8]基于小波分形理论,采用SVM算法对矿山爆破振动、岩石破裂及电磁干扰信号进行训练,用150组信号进行测试,最终达到94%的准确率,证明SVM算法可以较好的识别3类信号;姜鹏等[9]基于时频分析对微震和爆破的频率特征进行量化研究,建立了BP神经网络模型,对100组爆破和微震信号进行分类处理,模型达到98%的准确率,识别精度高,可为现场微震事件的识别提供参考;Giudicepietro等[10]将天然地震参数化获得频谱特征,将其输入多层感知器(MLP)中,在区分局部地震与区域地震和局部地震与远震地震时,可以得到97%以上的准确率,证明神经网络算法可以有效的用于地震数据分析;Lin等[11]构建了一种将深度卷积神经网络和空间金字塔池化相结合的模型,通过自动更新网络参数实现端到端的训练和测试,实现了多道微震波形的联合识别和分类;Perol等[12]利用卷积神经网络对天然地震进行波形监测,就单个波形进行定位研究,该神经网络方法在计算时间上优于其他检测方法,极大地缩短了地震定位需要的时间;Zhang等[13]建立了基于卷积神经网络的微震检测模型(CNN-MDN),在测试集中得到97.8%的高准确率,但模型收敛速度缓慢且模型对于未曾训练过的事件,识别准确率仅达到89%,泛化性较差。
目前,波形分类主要针对地震波形开展,与微震存在差异,此外模型中所用的训练和测试数据量较少。前人针对微震波形分类存在收敛速度慢、准确率差等缺点,本文针对岩石微破裂信号的智能识别开展研究。相比时程曲线,波形的频谱可以更好地反应介质的动力学特性,不同类型波形的频谱差异性更为明显,因而本文将快速傅里叶变换(FFT)引入微震波形的识别,采用卷积神经网络方法,将时程曲线、频谱、相位特征作为输入,进行微震波形的自动识别,在此基础上,引入投票机制,实现对事件类型的判别。
2 工程背景及数据
2.1 工程背景本文依托于引汉济渭工程秦岭输水隧洞的微震监测。隧洞全长81.779 km,最大埋深2012 m。隧洞位于秦岭西部山区,其地貌总体受构造控制,经长期水流侵蚀、切割,形成了较为复杂的地貌单元[14]。秦岭隧洞沿线主要岩性特征见表1。本文分析的数据在桩号K41+810~K45+730之间,岩石类型主要为闪长岩,其岩体完整,岩质坚硬。

表1 秦岭隧洞沿线主要岩性特征表
输水隧洞左右洞壁各布置3个传感器,传感器实时地采集监测范围内的各种频率的震动,当有一个传感器接收到超出设定阈值的信号时,截取所有传感器在此信号接收时刻前100 ms至后300 ms的数据,并形成相应的波形文件,每个波形事件由6个波形信号组成。传感器位置随着隧洞的掘进而向前移动,从而达到实时监测和采集的目的。传感器接收的原始波形如图1所示,其中事件时间为年-月-日_时-分-秒毫秒,纵坐标表示振幅的大小。

图1 原始波形
2.2 数据集本文选取2018年6月的5104个事件(共30 624条波形)作为训练集和验证集,再从2019年4月到2021年4月中随机选取两月数据作为模型测试需要的测试集,以便测试模型的泛用性。图2给出数据采集及数据标签生成过程,噪声等无效事件标记为0,微震事件标记为1。每一事件均包含6条波形,如波形最大幅值小于0.1 V时,无论波形形状如何,均标记为无效信号;反之则根据波形形状,标记为微震事件或无效事件。对于波形识别,以每条波形作为一次输入,随机将90%的数据作为训练集,10%的数据作为验证集,图3为训练集和验证集的数据分布。

图2 数据集来源

图3 训练集和验证集数据样本
3 信号的时频分析
3.1 快速傅里叶变换(FFT)微震信号是一个数字信号,将其进行离散傅立叶变换(DFT)便可得到频谱,形式如下:

式中:N为数字信号序列长度;k=0,1,…,N-1;x(n)为第n次采集信号所获得的数据;称为旋转因子。
根据旋转因子的周期性、对称性和可约性,可以将有序长度的DFT分解成短序列进行计算,从而得到一种快速进行傅里叶变换的算法,即快速傅里叶变换(FFT)。
3.2 噪声、微震信号的时频特征在实际工程中,工程师主要通过信号持续时间、波形幅值以及明显的振动衰减等特征进行微震、岩爆事件的识别,可能会存在部分波形难以判断的情况。为了更充分挖掘数据的隐藏特征,本文对波形信号进行快速傅里叶变换,将频域特征引入信号的识别和分类。
微震监测系统的采样频率为10 kHz。图4给出了不同幅值及持续时间的微震波形的FFT结果。图4(a)振幅较低、振动持续时间较短,该事件能量主要集中在0~250 Hz,主要频率位于60~70 Hz;随振动持续时间及振幅的增加,频谱的宽度相应增加,各频率振幅也逐渐增高(图4(b)、图4(c))。而对于强岩爆波形(图4(d)),由于超出传感器量程,频带变窄,幅值显著增大。总体来说,波形图中微震波形电压幅值基本高于0.1 V,平均幅值在1 V以上,其大小与微震源产生弹性波大小有关,可以明显分辨出P波和S波;频率主要集中在0~250 Hz,随着信号持续时间和幅值增加,频域中振幅的峰值随之向高频移动,频带变宽。

图4 微震波形频谱分析
图5给出几种常见无效数据的FFT结果。图5(a)为典型的噪声信号,其电压幅值较小,基本位于0.1 V以下,波形杂乱,断续震荡,其主要由500 Hz、1200 Hz等高频信号复合而来;图5(b)为信号监测过程中混入的电磁干扰,其类似于冲击信号,达到峰值后迅速衰减;图5(c)为机械噪声,特点为沿着时间轴反复震动,成条带状,从频谱图可以发现它是由几种高频的简谐振动信号组成;图5(d)为典型的无效信号,时程曲线成条带状,振幅小并无明显波动,且在频域上没有规律性。

图5 无效信号频谱分析
分析表明:微震和无效信号在时域和频域上都有独特的特征,但单从时域或频域上来很难将2类波形完全区分开,因而有必要综合考虑信号的时频特征来进行微震信号的识别和分类。
4 卷积神经网络模型
4.1 卷积神经网络卷积神经网络(CNN)[15-16]是一种包含卷积计算且结构具有一定深度的神经网络深度学习算法,能够利用输入数据的空间结构提取特征,在图像和语音识别方面取得了重要的突破。卷积神经网络通过卷积核和对输入特征进行运算,采用池化层对得到的特征进行子采样,最后经过全连接层将提取的数据特征集成并映射到所需要的输出类别中。CNN需要设置的超参数较少,更容易调试到较高性能,微震波形的识别与语音识别类似,因而本文采用卷积神经网络进行微震波形识别。
4.2 技术路线本文提出了基于信号时频特征的CNN微震信号识别方法。对于微震事件的识别,先从原始数据中选取波形,对其进行预处理操作;再将预处理后的数据带入傅里叶变换,把波形信号的时频域特征同时作为模型的输入,以此来训练模型参数,得到微震波形和无效波形的分类结果。最后根据分类结果进行投票,当模型判断一次事件的6条波形中有3条以上为微震波形时,认为本次事件为微震事件,否则为无效事件,得到事件识别结果(图6)。模型采用一维卷积神经网络,通过多层堆叠,提高多通道信号的特征抽象能力,将卷积神经网络提取的特征输出给全连接层,最后输出波形的类别。根据波形识别的结果,引入投票机制,判断事件的类别。为了充分的验证模型对微震事件识别的准确性,将得到的事件波形划分为训练波形数据集和测试波形数据集。首先使用训练数据集对模型进行训练,然后使用测试集分别对模型进行测试,验证模型的有效性[17]。

图6 模型识别流程图
4.3 模型构建模型分为输入、特征提取和输出模块,以波形数据、频率和相位作为输入,采用一维卷积神经网络对特征进行提取和识别,对每个输入采取不同的特征提取模块,最后通过全连接层将所有特征组合进行识别。模型包含24个卷积层、9个池化层、5个全连接层和1个平铺层,其中卷积核大小为3,步长为1,卷积核的个数和全连接层的大小如图7所示。
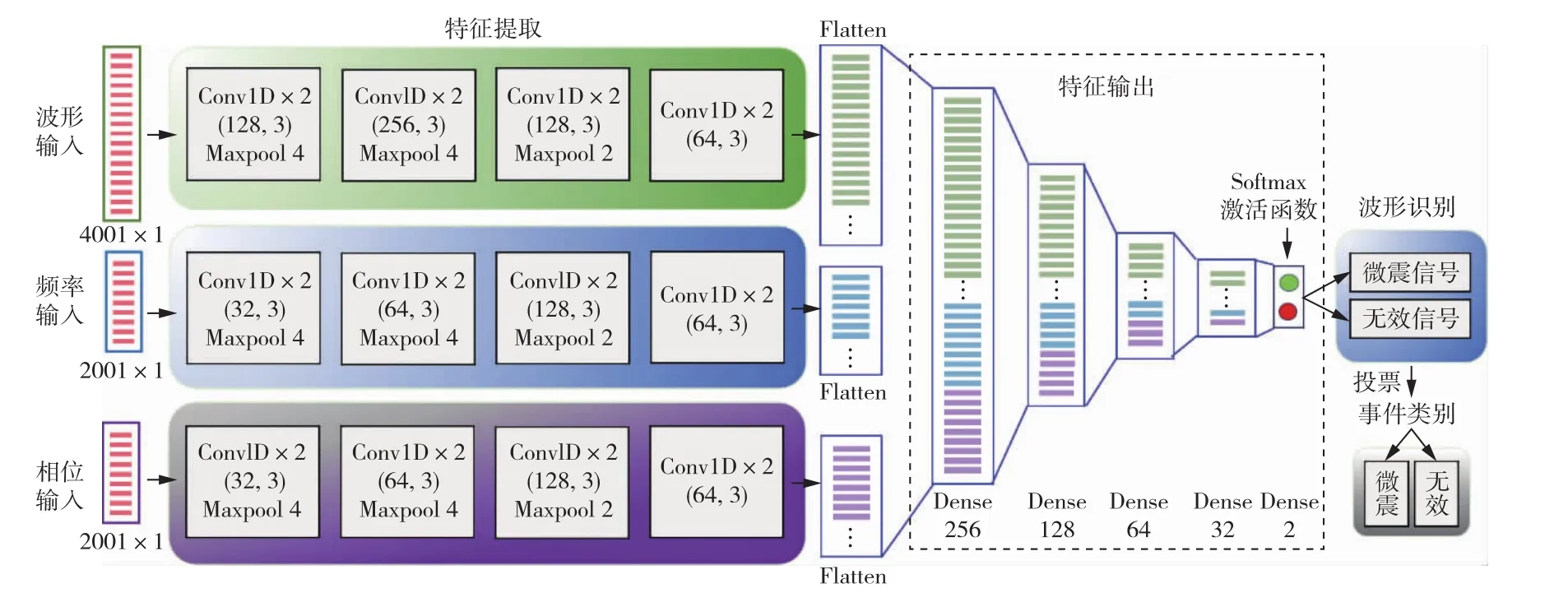
图7 CNN模型结构
模型的损失函数采用交叉熵函数。交叉熵是真实数据分布所包含的信息熵H(X)[18-19]。在分类问题中使用交叉熵能更准确地衡量分类错误的误差,在反向传播中取得更好的梯度从而更快更好地进行模型参数的更新。为了提高模型的收敛性,模型训练时宜在前期采用较大的学习率,在后期采用很小的学习率,因而采用Adam算法,可以自动根据梯度的指数移动均值自动调整学习率。为了尽可能挖掘模型潜力并减少不必要的迭代次数,采用回调函数,当本轮验证集损失值大于3轮训练前的损失值,则将学习率降低50%,如5轮训练后,验证集损失值仍未下降,则停止训练。
5 模型训练与测试
5.1 模型训练结果在实验中,训练世代上限设置为20,当世代达到第9轮时,模型损失值相较于第7轮没有下降,模型训练完成。整体训练过程如图8所示。对于波形识别,在第1轮世代中,模型的准确率已经达到86%之上,随着世代的增加,模型训练集、验证集损失和准确率均趋于稳定,训练集的准确率达到97.17%,验证集的准确率达到93.23%。

图8 模型训练结果
针对微震事件的识别,将2019年4月的无效事件和2020年3月的微震事件进行混合,共2449个无效事件,14 694条无效波形;1321个微震事件,7926条波形。按照上述原则进行标签。将总共22 620条波形,和它们对应的经过傅里叶变换后的频率和相位作为测试集输入模型,得到如图9所示的分类结果图。

图9 分类结果图
根据图9可以看到,对于无效事件,模型将86次事件识别为微震事件,2363次事件识别为无效事件,无效事件识别准确率为96.49%。对于微震数据,从图9右可以看到模型将1260次事件识别为微震事件,识别事件准确率为95.38%。可见面对大量的微震和无效信号,模型可以准确识别微震和无效事件。
5.2 模型测试与分析从无效和微震事件中各随机选出100次事件进行分析,通过不同的输入和不同的模型对比,将每个模型调试参数至准确率最高作为测试结果(表2)。可以看出以波形为单一输入,模型对微震事件的识别率仅为86%,单纯采用频率和相位数据,并无法明显提高模型的准确率。在输入信号的时频数据后,模型准确率明显提高,这表明模型能够对输入的数据进行很好的拟合,为现场微震事件的识别提供参考,同时模型对于随机事件的准确识别可以证明模型具有很好的普适性。

表2 不同输入对比分析
在同时输入波形、频率和相位数据后,模型对100次微震事件,即600条波形信号进行识别,仅有两条波形识别错误,波形识别成功率99.7%,事件识别成功率为100%。为探究模型对两条波形识别错误的原因,对这两次事件进行研究,表3为两次事件的实际预测结果,图10、图11为两条波形信号的波形图和频谱图。

表3 部分波形识别结果

图10 事件2020-03-04_19-53-10112通道1的波形和频谱图

图11 事件2020-03-04_23-55-14714通道1的波形和频谱图
对于事件2020-03-04_19-53-10112通道1和事件2020-03-04_23-55-147141通道1来讲,在时域上振幅明显,符合微震信号的波形特征,但在0.4 s内一直伴随着较大的机械噪声,导致两条信号在频域上显示噪声的波形特征,因此模型识别错误。总体来说,在这100次微震事件中模型表现优秀。对于100次无效事件,有96次预测成功,模型微震和无效事件总体识别成功率有98%。
表4给出本文模型和其他文献[8,13,20]的对比结果。本文所用数据量显著大于同类研究,模型准确率与同类研究相当,模型具有较好的概化能力。

表4 不同方法对比分析
6 结论与讨论
本文以快速傅立叶变换为手段分析了在隧洞掘进过程中微震信号的时频特性,利用卷积神经网络进行了微震事件的快速识别。最终得到如下结论:
(1)在微震波形识别中,同时考虑波形信号的时频特征,利用微震和无效信号在时域和频域上各自的不同,将波形数据、频率以及相位同时作为模型的输入,可以有效的识别微震和无效波形,对于模型准确率的提升具有至关重要的作用。
(2)建立了包含2449个无效事件,1321个微震事件的样本库。提出了基于信号时频特征的微震波形识别模型,在经过9次世代后模型迅速收敛,且在测试中,对大量波形事件识别,模型有着96.1%准确率。证明它在运用人工智能解决波形分类问题上有着广泛的适用性。
(3)在结果分析中,对200次事件进行识别,通过对比发现,模型在输入数据时考虑同时输入时频特征可以有效提高信号的辨识度,且在波形信号识别方面相比于其他方法具有足够高的准确率,能够在数据量成倍增加的情况下依旧有着高的精准度。
(4)模型对于微震和无效事件识别的高准确率,可以减少工程师在岩爆预测中所面临的数据量大和模型训练拟合慢的负担,同时将微震事件单独分类出来也有利于对岩爆预测准确率的提高。波形识别模型的高准确率预示着通过人工智能处理岩爆问题有着极大的可行性。
(5)利用机器学习算法对微震信号进行了学习,对于不同工程,其共性是微震和噪声信号在时频域上有明显的差异,故而本文提出的模型可以适用于引汉济渭输水隧洞之外的工程。需要指出的是,本文仅对大量的波形中识别出微震波形进行了初步研究,虽然模型整体表现出良好的性能,但卷积神经网络属于有监督的学习算法,模型的准确率依赖于数据标签的质量,因此对于微震波形的准确识别需要更深入的研究。

