考虑流固耦合的输水管道水锤不确定性及管道风险分析

吕国亮

（华东工程咨询有限公司，浙江 杭州，310014）

水锤现象是指输水系统运行过程中，因水力机组意外断电、阀门等部件的误操作或水文因素导致水池水位的大突变等原因，造成流速剧烈变化，致使水体压力出现较大波动。水锤压力与管道参数、管内流体参数、管道工作环境有关，上述变量均为不确定变量，因此水锤压力也是不确定变量。郭强[1]研究了泵站出水管，假设参数的不确定性，采用蒙特卡洛法模拟，得出水锤变异性是引起管道风险主要因素。郭文铸等[2]考虑水-机-电相关参数的不确定性，揭示水锤极值服从对数正态分布。在郭文铸基础上，张芹芬[3]考虑了导叶初始开度不确定性，模拟分析管道输水系统极限水击压力分布。上述成果表明，水锤不确定分析已经取得一定成果，但流固耦合现象在研究中考虑较少。

由于材料泊松比的存在，管道径向的膨胀或收缩导致管壁轴向振动，反作用于水锤压力，这叫流固耦合现象，同时考虑耦合现象进行计算的水锤叫耦合水锤。水锤荷载引起流固耦合现象较为明显，为更精确地预测水锤压力，需考虑流固耦合[4]。

耦合水锤与流体及输水系统参数密切相关，且两者均为不确定变量，故耦合水锤不确定性复杂，有必要对其进行不确定性分析。

1 数值模型及求解方法

1.1 控制方程

假定径向管道为准静态运动[5]，不考虑液体和管壁中径向惯性力及重力，管壁材料均匀、各向同性、线弹性强、变形小，考虑流体粘性。流体轴向运动方程：

考虑可压缩性的流体连续性方程[6]：

考虑管道结构对流体的阻抗，根据文献[7]得管道轴向运动方程[8]：

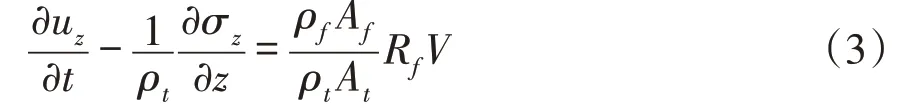
流体的压力变化与管道的应力、速率之间的关系是：

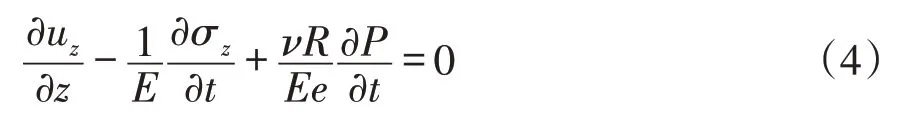
式中，P为流体压力；V为流体速度；σz为轴向管应力；uz为轴向管速；E为管材杨氏弹性模量；ν为管材泊松比，e为管壁厚度；At、Af分别为管壁截面积和管道内截面积；ρt、ρf分别为管材和流体密度；K为流体体积模量；R f为流体的粘滞系数；R为管道半径。

1.2 数值方法

由于输水系统中存在水锤波和应力波，特征线法不易求解。若采用有限体积法求解，每个控制容积进行积分求解，且积分方程具有明确物理意义，则其计算结果较精确。故采用有限体积法求解模型，利用控制容积在控制体内进行积分，此时输水系统的结构和流体作为一个整体，随后在控制容积内从时间t到t+Δt对控制方程积分。以方程（1）为例，控制容积内积分方程：

同时应用时间中心差分的Crank-Nicolson隐式格式对偏微分项进行处理[9]，得到具有二阶精度且无条件稳定的水锤方程离散格式：

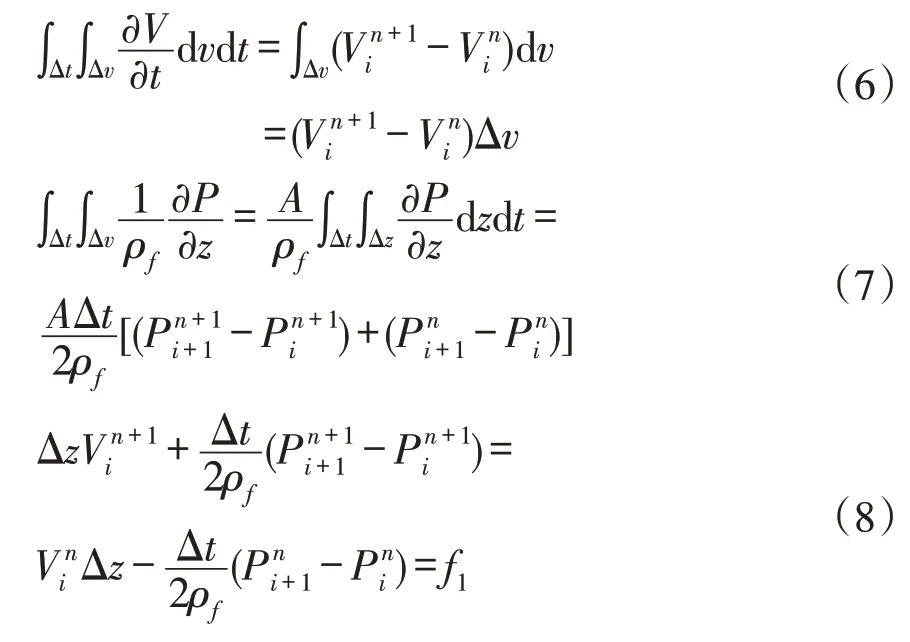
相同原理可得交错计算节点差分方程：

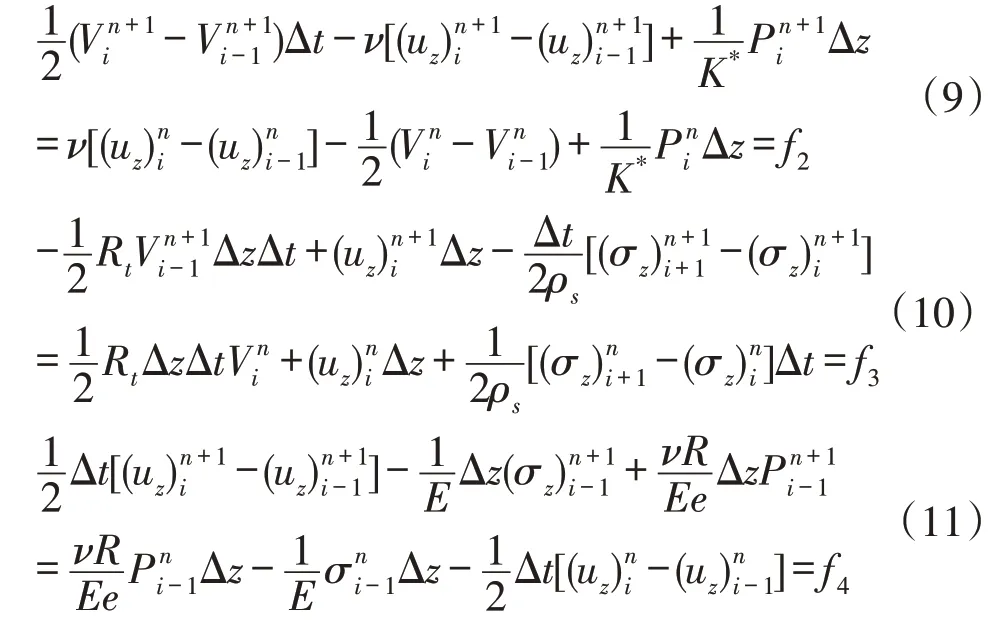
2 结果及讨论

2.1 确定性分析

考虑输水系统中流固耦合响应，进行耦合水锤计算，结果如图1所示。管道长L=30 m，管道内径R=0.1 m，管壁厚度e=0.01 m。管道入口与水库刚性连接，管道出口与阀门刚性连接。阀门关闭，导致应力波和压力波，均向上游传播，且两种波相互影响。由图1可知，管道振动引起管内流体扰动，导致耦合压力曲线呈不规则变化。其中应力波作用导致压力在变化过程中产生局部突变。具体原因为：由于应力波速近似为压力波速三倍，故在半个周期内，压力变化可分为三部分：（1）管道膨胀，释放压力，形成压降；（2）当管道处于压缩状态，对管内流体形成一种“泵”效应；（3）随后管道又处于膨胀状态，形成压降。故考虑流固耦合，管内水锤变化曲线更加尖锐（“泵”效应导致考虑流固耦合的水锤峰值更高，水锤频率也更大，引起更大的风险）。

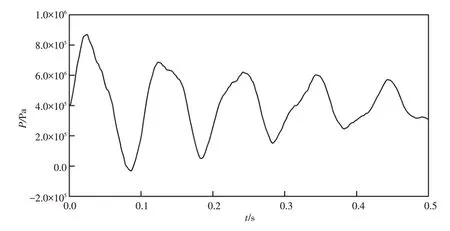
图1 考虑流固耦合水锤压力随时间变化Fig.1 Curve of water hammer taking FSI into account

将数值计算结果与文献[10]实验结果进行对比，验证有限体积法求解适用性（实验数据由英国Dudee大学所得，管内刚好无压满流，由于现实中流固耦合时刻存在，无法通过实验获得不考虑流固耦合的水锤，故此实验仅验证了数值模型可靠性）。由图2可知，数值计算结果与实验结果相吻合，表明流固耦合四方程适用于耦合水锤分析，且计算结果精确度较高，误差较小。

图2 实验结果与数值结果相吻合Fig.2 Experimental data and numerical d ata are identical

2.2 不确定性分析

耦合水锤与输水系统和流体参数相关，且依赖于输水管道工作环境。输水系统和流体参数具有不确定性，且输水系统工作环境复杂，这些因素导致耦合水锤具有不确定性。

杨惠莲和张涛[11]对多组钢材强度实验进行了统计分析，得到钢材强度σR服从正态分布，变异系数为0.095。在实际工程中，输水系统与许多参数相关，但参数相关性分析和参数概率分布情况在数理统计分析方面鲜有研究。根据误差理论、中心极限定理[12]和王长新[13]等研究成果，将难以确定的分布视为正态分布，并认为均值为设计值，标准差按均值的5%选取。随机变量的分布特性与统计特征值见表1。

根据表1所示随机值，耦合水锤不确定性分析结果如图3所示。当管内压力大时，管道导致的压降和“泵”效应更加明显，耦合水锤变异性增大。故为了更好地分析耦合水锤，可仅分析耦合水锤峰值的不确定性。对比图1和图3可知，不确定性分析相对耦合水锤数值（不确定性分析结果/确定性分析结果）在0.95~1.05之间变化。但在相对耦合水锤为1.05仅出现1次，其概率可忽略，如图4所示。为保证输水系统在水锤荷载下正常运行，设计时考虑相对耦合水锤为1.04。

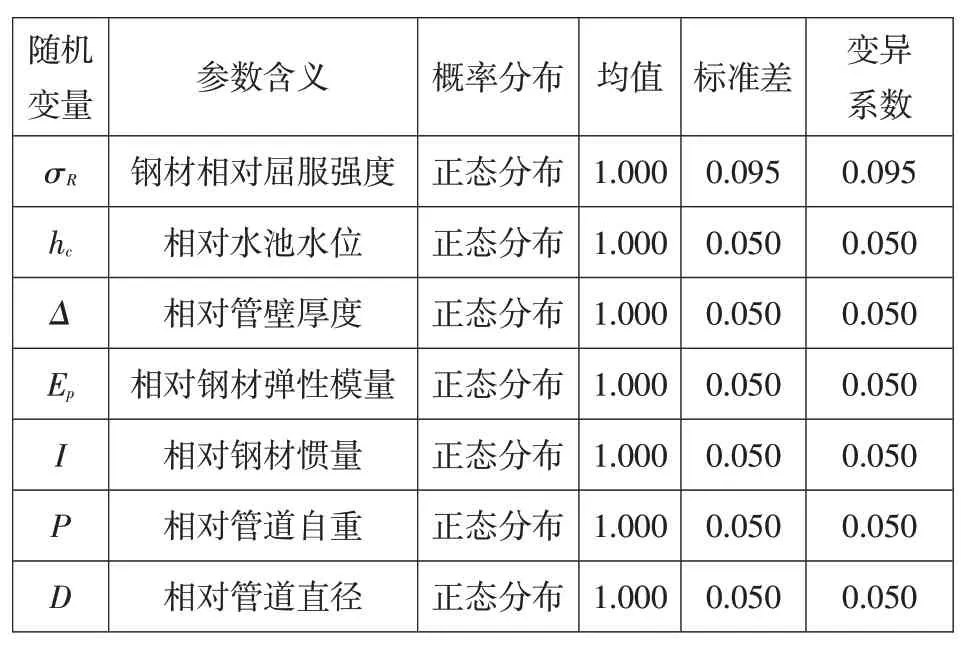
表1 主要随机变量的分布特性与统计特征值Table 1 Distribution characteristics and statistical eigenvalues of main random variables

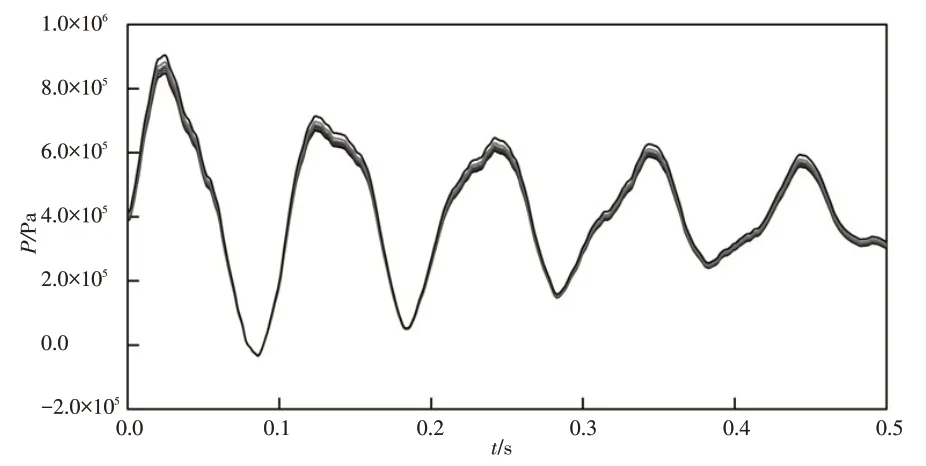
图3 耦合水锤不确定性分析结果Fig.3 Uncertainty analysis results of coupled water hammer

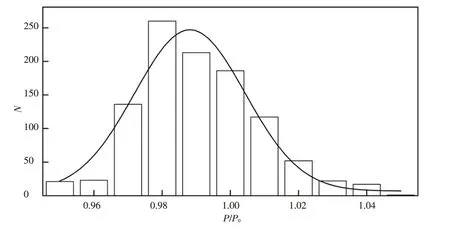
图4 耦合水锤不确定性分析结果直方图Fig.4 Histogram of uncertainty of coupled water hammer

不确定分析结果的直方图如图4所示。在置信水平为90%、95%和99%进行假设检验，得到耦合水锤为P-Ⅲ型分布，且相对耦合水锤的均值为0.99，相对耦合水锤标准差为0.18。

2.3 耦合水锤荷载下管道风险分析

建立极限状态方程Z=[σ]-max(σθ)[14-15],其中[σ]为管道容许最大环向应力；σθ为考虑流固耦合环向应力，σθ=PR/e。采用蒙特卡洛法计算[15]，得出主要不确定因素与输水管道风险值Pf关系如图5所示。相对于其他参数，耦合水锤变异系数大于0.05时，输水系统风险随耦合水锤变异系数变化明显，进一步说明了耦合水锤不确定性分析的必要性。但耦合水锤变异系数小于0.05时，风险值变化较小，此时的耦合水锤可视为确定变量。由图4统计结果，简单输水系统中耦合水锤变异系数为0.18，其导致的风险应该更加被重视。相对于耦合水锤，液体压缩体积模量和管道参数对输水系统风险影响较小，可视为确定性量[16]。

图5 输水管道风险随变异系数变化Fig.5 Variation of pipeline risk with coefficient of variation of pa⁃rameters

分别考虑耦合水锤为确定性变量和不确定性变量，模拟次数为103~106，不同模拟次数下输水系统风险值如表2所示。当模拟次数较少时，由于精度不够，导致不确定性分析和确定性分析相差不大，甚至风险值相等。随着模拟次数增加，两种情况下风险值差距增大。不考虑水锤随机性计算所得风险值偏小，可能造成设计上的冒进，从而增大事故概率。同时，当模拟次数大于105时，输水系统风险值相对误差小于1%。故为保证结果精度，模拟次数应大于105。

表2 不同模拟次数的确定性与不确定性分析结果Table 2 The certainty and uncertainty results with different cal⁃culation times

3 结语

（1）不确定性分析获得最大耦合水锤比确定性分析结果大4%，若依据传统的确定性分析结果进行设计，会增大输水系统失效概率。

（2）考虑输水系统参数和工作环境的不确定性，相对耦合水锤服从均值0.99、标准差为0.18的P-Ⅲ型分布。

（3）耦合水锤的不确定性是输水系统风险的主要起因，为更准确分析风险值，模拟次数应大于105。