彭冲涧小流域基流变化特征及其归因分析
盛 菲,刘 政,刘士余*,李 俊,余敏琪
(1.江西农业大学 国土资源与环境学院,江西 南昌 330045;2.江西省鄱阳湖流域农业资源与生态重点实验室,江西南昌 330045;3.华中农业大学 资源与环境学院,湖北 武汉 430070)
【研究意义】基流作为径流的重要组成部分,是枯水径流的主要补给来源[1],也是地下水资源评价和流域水资源管理的重要内容,其变化特征与流域气候条件、自然地理属性及人类活动等密切相关[2-3]。近年来,基流变化特征及其影响因素逐渐成为研究热点。【前人研究进展】国内的基流相关研究主要集中在黑河流域[4-6]、黄土高原[7-9]、黄河流域[10-12]等。例如,Zhang 等[6]在黑河上游的研究显示,人类活动对基流变化的贡献率高于气候变化的贡献率;张华等[4]指出降水对黑河上游基流量的变化具有显著影响,而人类活动导致的森林面积减少,使得流域基流量减少且更易受气候变化的影响。Wu 等[9]以黄土高原的11个流域为研究对象,得出在1971—1999 年和2000—2014 年这2 个时期,气候变化对基流量变化的贡献率(27%、24%)小于人类活动(73%、76%),且潜在蒸发散对基流量的影响大于降水。王雁林等[12]指出黄河河川基流量的变化受降水量变化、地下水开采、水土保持等因子的综合作用;梁四海等[10]在黄河源区的研究表明,降水和气温是基流量周期变化的主导因素。同时,国外也有许多学者开展过大量相关研究。例如,Ahiablame 等[13]在美国密苏里河99个流域的研究表明,降水、农业用地每增加1%,基流量分别上升1.5%、下降0.2%。Juckem 等[14]以美国Kickapoo 流域为研究区,得出该流域基流量的增加与降水量增加、暴雨径流减少、下垫面入渗率的改变有关。Smettem 等[15]在澳大利亚南海岸的研究指出,基流的变化与气温、土地利用变化等因素有关。Mwakalila 等[16]在坦桑尼亚12 个半干旱集水区的研究显示,降雨量高、蒸发散低的集水区产生的基流较大。
【本研究切入点】综上可知,基流变化是多因素共同作用的结果,且国内外学者已开展了大量相关研究,但未能明确各显著性影响因素贡献率的大小;同时,关于基流周期变化的成因分析更是少见。【拟解决的关键问题】因此,本文以彭冲涧小流域为研究对象,分析基流的趋势和周期变化特征;找出基流趋势变化的显著性影响因素,并计算其对基流的相对贡献率;识别与基流具有相同显著周期的影响因素,借助小波系数相关性判定基流周期变化的主导因素。研究成果对小流域基流变化内在机理的探究、流域水资源的合理配置等方面具有重要意义。
1 研究方法与数据来源
1.1 研究区概况
彭冲涧小流域位于江西省九江市都昌县境内(29°31′44′′~29°32′56′′N,116°25′48′′~116°27′7′′E,图1),集水面积为2.90 km2,属南方红壤区。流域内无人口居住,也未修建水利、水土保持工程。气候类型属亚热带湿润季风气候,多年平均降水量、径流深、气温分别为1 589 mm、761 mm 和17.6 ℃。流域四周闭合,地形西北高、东南低,海拔80~560 m,主要地层出露以浅变质岩、花岗岩和灰岩为主。流域内植被类型主要为杉木(Cunninghamia lanceolate)林,20世纪80年代杉木林遭到砍伐后,一直处于恢复过程,森林覆盖率由80%上升至98%,森林蓄积量从1.2 万m3上升至2.5 万m3。彭冲涧水文站设立于1981 年,持续观测降水、径流等数据至今。

图1 彭冲涧小流域示意图Fig.1 Sketch map of the location of Pengchongjian small watershed
1.2 数据来源
本文基于彭冲涧水文站1983—2017 年的逐日降水、径流、气温等观测资料,整理、计算得到季节、年尺度上的降水、径流和气温。通过数字滤波法对逐日径流量进行基流分割,计算得到年基流量;通过水量平衡公式计算得到年蒸发散[17];通过ENVI5.0软件对遥感影像数据进行处理并计算得到NDVI值[18]。
1.3 研究方法
1.3.1 数字滤波法 数字滤波法是基流分割中常用的方法,该方法适用性较强,得到了广泛应用[19-21]。其主要原理是利用数字滤波器将高频信号(地表径流)和低频信号(基流)分离,进而达到基流分割的目的。其滤波方程为:

式(1)和(2)中:Qt、Q(t-1)分别为t、t-1时刻的径流量(m3/s);Qdt、Qd(t-1)分别为t、t-1时刻的地表径流量(m3/s);Qbt为t时刻的基流量(m3/s);β为滤波参数。已有研究表明[22],β=0.90,T=2为彭冲涧小流域的最佳参数。因此,本文的基流量是采用以上参数分割得到的。
1.3.2 小波分析 小波分析是一种反映时间序列周期变化特征的常用方法[23],基于Morlet函数的连续小波分析广泛应用于识别信号的周期震荡及水文气象要素的特征分析[24],主要过程如下:
设f(t)为连续函数,则其小波系数Wf(a,b)为:

小波方差Var(a)为:

式(3)和(4)中,a为尺度因子,b为平移因子,(x)为Ψ(x)的共轭。
1.3.3 Mann-Kendall 检验法 采用Mann-Kendall 检验法对时间序列进行趋势检验。其检验统计量|Z|大于1.96(2.58)时,表示趋势达到0.05(0.01)显著性水平[25-26],文中,**代表0.01 显著性水平,*代表0.05 显著性水平,NS代表不显著。
1.3.4 逐步回归分析法 逐步回归分析法的基本原理是将自变量逐个引入模型,每引入一个自变量后都需进行F检验(检验此时逐步回归方程的显著性),并对已经引入的自变量逐个进行T检验(检验自变量对因变量是否有显著影响),反复进行上述过程,直至所有显著性变量全部被引入[27]。
设多元线性回归方程为:

式(5)中,αi为各自变量的偏回归系数,Xi为自变量。
由于各自变量单位不一致,需对各自变量进行标准化处理。其标准化公式为:

式(6)中,Xij为原始数据为标准化后的数据为平均值;Si为标准差。
为体现各因变量相对贡献率的大小,其权重计算公式如下:

式(7)中,Li为各自变量的标准化回归系数;qi为各自变量的权重,其中
2 结果与分析
2.1 彭冲涧小流域基流变化特征
2.1.1 基流趋势变化特征 图2 显示,彭冲涧小流域1983—2017 年的基流量总体呈下降趋势,变化率为1.682 mm/a,多年平均值为162.4 mm;基流量的最大值为305.9 mm(1998 年),最小值为72.8 mm(2007年)。且基流量的年际变化趋势不显著,其变差系数Cv为0.34,说明基流量的年际变化幅度较小。

图2 1983—2017年彭冲涧小流域基流量年际变化Fig.2 Inter-annual variations in baseflow for the Pengchongjian small watershed during 1983—2017
2.1.2 基流周期变化特征 由图3a可知,年基流量存在3~6年、8~12年、15~20年和25~32年4种尺度的周期变化,且在这4种尺度上,基流量分别出现了8次、5次、2次和2次“丰—枯”交替。从图3b可以看出,年基流量存在4 个明显的峰值,其中最大峰值对应的时间尺度为32 年,即第一主周期,该阶段能量波动最为剧烈;第二、第三、第四峰值对应的时间尺度分别为6 年、10 年、17 年,依次为年基流变化的第二、第三和第四主周期。

图3 1983—2017年彭冲涧小流域基流量小波系数实部等值线图(a)和小波方差图(b)Fig.3 Real part contour graph(a)and wavelet variance graph(b)for the baseflow from the Pengchongjian small watershed during 1983—2017
为进一步反映基流的周期变化特征,选用4 个主周期,绘制对应尺度上的小波系数实部过程线(图4)。由图4可知,年基流量的周期变化存在尺度差异,随着时间尺度的增加,其丰枯交替速率逐渐减弱。不同的时间尺度,年基流量所处的丰枯阶段也不同,说明基流的周期变化与时间尺度密切相关。

图4 不同主周期对应的小波系数实部过程线Fig.4 Real part process of wavelet coefficient with different dominant periods
2.2 基流变化归因分析
本文在前人的研究基础上[14,18,28-31],并结合小流域实际情况,选取降水、蒸发散、平均气温、最高气温、最低气温和NDVI作为基流的影响因素。
2.2.1 各影响因素变化趋势分析 6 个基流影响因素的年际变化特征见图5。1983—2017 年彭冲涧小流域的降水、蒸发散、平均气温、最高气温、最低气温、NDVI 均呈上升趋势,其变化率分别为1.459 mm/a、6.063 mm/a、0.039 ℃/a、0.017 ℃/a、0.055 ℃/a 和0.004/a,平均值分别为1 589.1 mm、828.0 mm、17.55 ℃、36.99 ℃、-4.11 ℃和0.77;除平均气温和NDVI的变化趋势极显著、蒸发散的变化趋势显著外,其他因素的变化趋势均不显著。
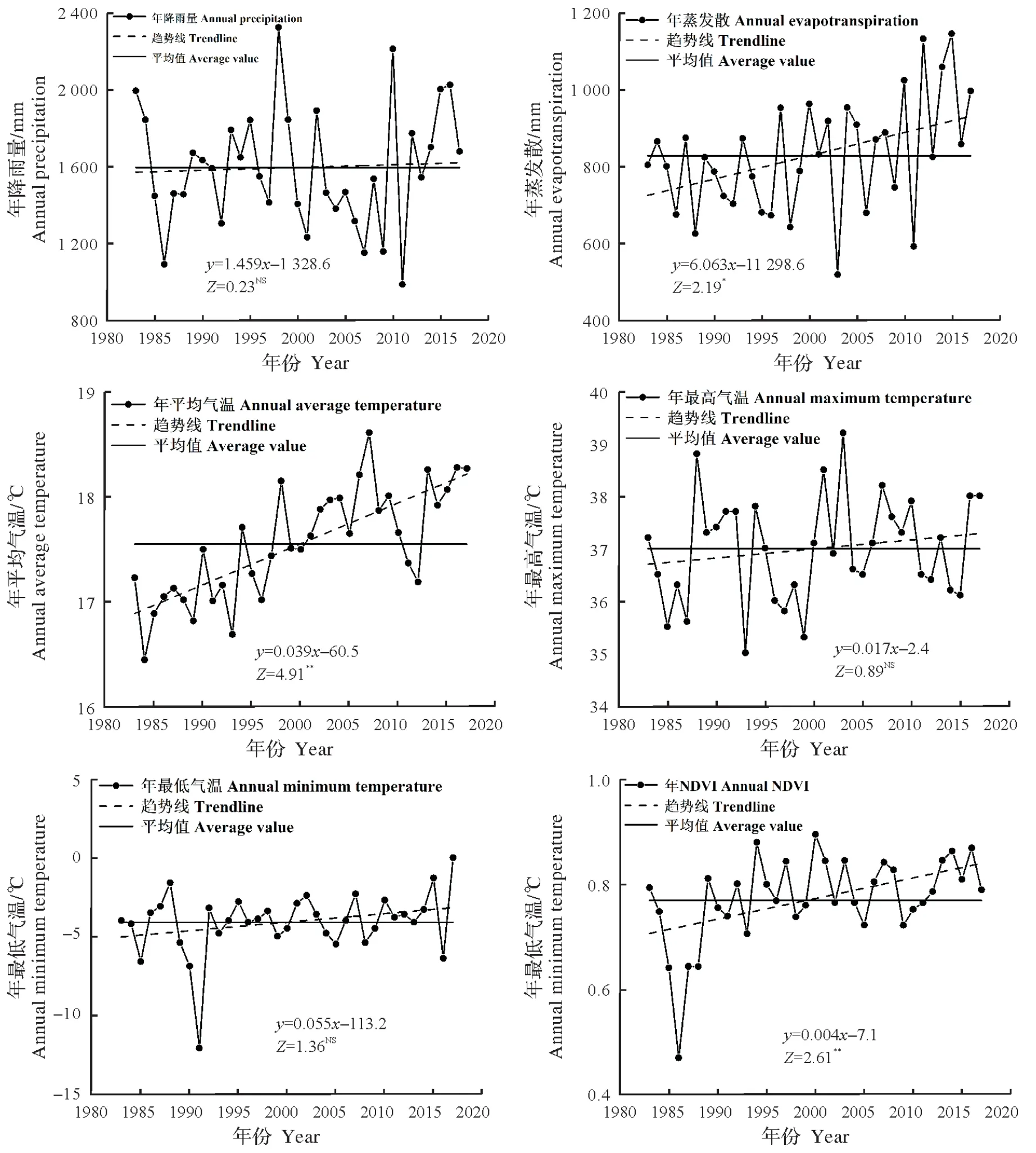
图5 1983—2017年彭冲涧小流域基流影响因素的年际变化Fig.5 Annual variation of influencing factors of baseflow for the Pengchongjian small watershed during 1983—2017
2.2.2 基流趋势变化归因分析 为量化各影响因素对年基流变化的影响程度,以各影响因素为自变量,年基流量为因变量,进行逐步回归分析,得到3个逐步回归模型,结果见表1。
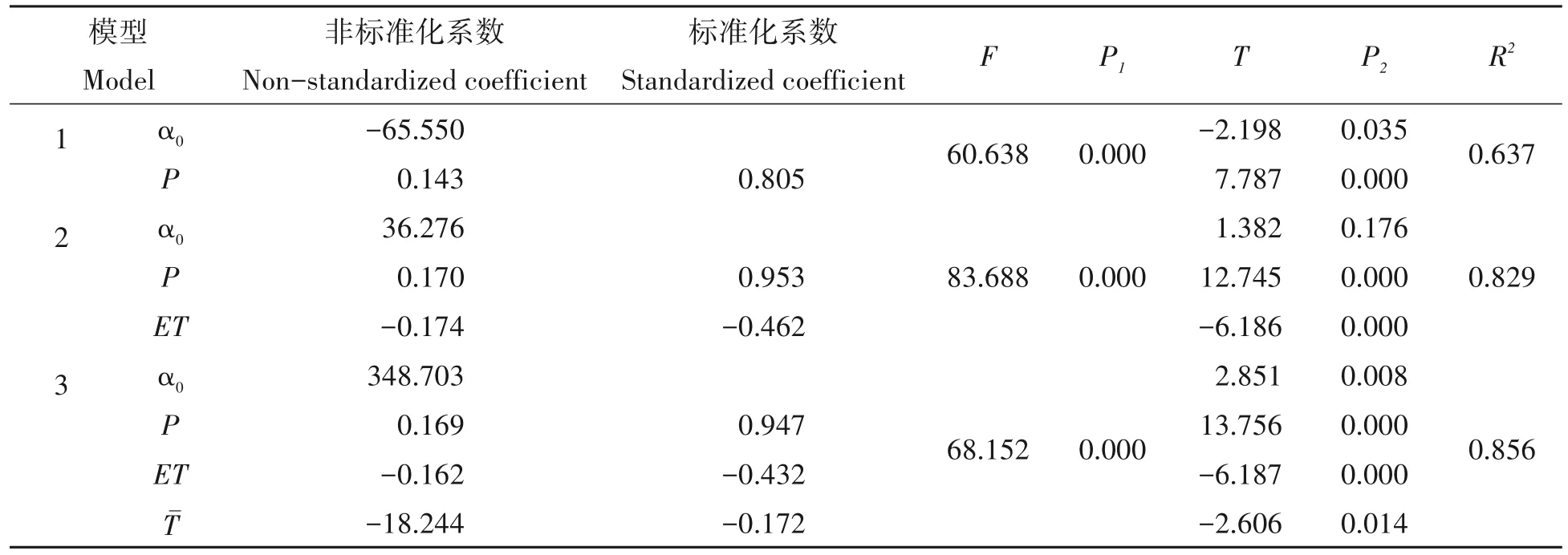
表1 1983—2017年逐步回归计算结果Tab.1 Stepwise regression computation results in 1983—2017
表1显示,3个逐步回归模型的决定系数R2逐渐增大,模型3的R2=0.856,拟合程度最高,对应的方程为:

式(8)中,Qb为年基流量,P为降水,ET为蒸发散,Tˉ为平均气温。经过F检验后,方程显著性成立。
从表1还可知,模型3中共有3个自变量通过了T检验,分别是降水、蒸发散和平均气温,说明这3个因素为基流变化的显著性影响因素。其回归系数分别为0.947、-0.432、-0.172,三者对基流的影响程度排序为:降水>蒸发散>平均气温。
为验证逐步回归方程的模拟效果,将彭冲涧小流域1983—2017年的基流分割结果与公式(8)的计算结果进行比较(图6)。经计算,由数字滤波法得到的分割值与逐步回归方程模拟值间的平均相对误差Re=0.003,决定系数R2=0.869,说明逐步回归方程的模拟效果较好。

图6 彭冲涧小流域基流分割值与模拟值对比Fig.6 Comparision of the divided and simulated values of baseflow in Pengchongjian small watershed
由上文权重计算公式(7)可得,降水、蒸发散、平均气温对基流的相对贡献率大小分别为61.1%、-27.9%、-11.0%。可知,降水对基流起促进作用,蒸发散和平均气温对基流起抑制作用,且降水对基流的相对贡献率最大,是最主要的显著性影响因素。
2.2.3 基流周期变化归因分析 研究表明,当基流与其影响因素具有相同的显著周期时,通过分析显著周期的小波系数相关性,可判定基流周期变化成因[10]。各影响因素的小波系数实部等值线如图7所示。
由图7可知,不同影响因素的显著周期存在一定差异。降水的显著周期为3~6年、8~12年和25~32年;蒸发散的显著周期为3~6年、8~16年和22~30年;平均气温的显著周期为3~6年和12~23年;最高气温的显著周期为3~6 年、8~12 年和18~24 年;最低气温的显著周期为6~8 年、10~15 年和20~28 年;NDVI 的显著周期为3~6年、8~16年。可以看出,降水与基流具有3~6年、8~12年、25~32年这3个相同的显著周期,最高气温与基流具有3~6年、8~12年这2个相同的显著周期,蒸发散、平均气温、NDVI与基流具有3~6年这1个相同的显著周期,而最低气温与基流无相同的显著周期。

图7 降水(a)、蒸发散(b)、平均气温(c)、最高气温(d)、最低气温(e)、NDVI(f)的实部等值线图Fig.7 The real part contour graph of precipitation(a),evapotranspiration(b),average temperature(c),maximum temperature(d),minimum temperature(e)and NDVI(f)
小波系数相关分析结果显示(图8),在3~6 年的显著周期上,降水、平均气温、蒸发散与基流的相关系数r分别为0.94、0.75和-0.72,均呈极显著相关;而最高气温、NDVI与基流的相关性较低,r分别为0.39和-0.40。由图9 可知,在8~12 年的显著周期上,降水、最高气温与基流呈极显著相关,r分别为0.95 和0.62。在25~32 年的显著周期上,降水与基流的相关系数r达到0.99,呈极显著相关(图10)。
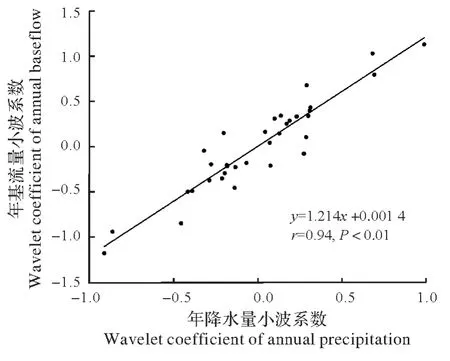

图8 3~6年显著周期上的小波系数相关性Fig.8 Wavelet coefficients correlation with significant period of 3-6 years

图9 8~12年显著周期上的小波系数相关性Fig.9 Wavelet coefficients correlation with significant period of 8-12 years

图10 25~32年显著周期上的小波系数相关性Fig.10 Wavelet coefficients correlation with significant period of 25-32 years
可以看出,在3~6年、8~12年、25~32年这3个显著周期上,降水与基流的小波系数相关性均最高,说明基流周期变化的主导因素为降水。这可能由于降水是基流的主要补给来源,降水的变化将直接影响基流的补给和排泄,降水的周期变化特征也将体现在基流的周期变化之中[10]。其次,在3~6年的显著周期上,平均气温、蒸发散与基流均具有较好的相关性,而最高气温、NDVI对基流的影响较小。同时,最高气温在8~12年的显著周期上与基流的相关性也较低。
3 结论与讨论
3.1 讨论
3.1.1 基流趋势变化成因 如前文所述,降水、蒸发散和平均气温是基流趋势变化的显著性影响因素,三者对基流变化的相对贡献率大小分别为61.1%、-27.9%、-11.0%。其中,降水对基流形成起促进作用,且贡献率最大,可能是因为流域基流主要由降水补给,降水的变化将直接导致基流的变化[10]。蒸发散对基流的贡献率次之,且蒸发散与基流呈负相关。图5 显示,彭冲涧小流域1983—2017 年的降水、蒸发散和平均气温均呈上升趋势,且蒸发散的变化率(6.063 mm/a)远高于降水(1.459 mm/a),蒸发散的快速上升将影响降水对基流的补给;而平均气温对基流的贡献率最小,且与基流呈负相关,这可能是由于气温的上升将增大流域蒸发散[32],进而间接影响基流的变化。
本研究结果与张华等[4]在黑河流域上游、Ahiablame等[13]在美国密苏里河99个流域、Ficklin 等[28]在美国流域、Li 等[33]在鄱阳湖流域的研究结果相似,与Wu 等[9]在黄土高原、王敬哲等[34]在呼图壁河、李倩等[35]在开都河和玛纳斯河流域的研究结果相差较大(表2)。这可能是气候、土壤、植被、地形等条件的不同所致[2-3]。例如,黄土高原属于典型的半干旱地区,气候干燥,且在过去20 多年实施了退耕还林(草)等措施[9],而彭冲涧小流域位于湿润地区,基流主要受降水补给,且无人类活动干扰,因此该流域与黄土高原基流变化的主导因素存在差异。

表2 前人研究结果Tab.2 Previous research results
3.1.2 基流周期变化成因 小波分析结果显示,基流周期变化主要由降水所致,二者存在3 个相同的显著周期,其小波系数相关性均最高,这与梁四海等[36]研究结果相似。可以看出,无论是趋势变化,还是周期变化,降水均是基流变化的主导因素,其周期变化规律也将体现在基流的周期变化之中[10]。众所周知,降水经林冠层和枯枝落叶层后到达地表,部分再经土壤入渗而成为壤中流和地下径流,壤中流和地下径流是基流的主要补给来源,其滞后性直接导致基流的时滞性[37-38]。如图11 所示,在6 年这一主周期上,降水与基流的小波系数振幅顶点之间存在一定时间差异,而这种时滞性的存在,会在一定程度上影响两者小波系数相关性的大小。

图11 降水量和基流量的小波系数对比Fig.11 Comparision of the wavelet coefficients of precipitation and baseflow
在3~6 年的显著周期上,平均气温和蒸发散[39]对基流的影响仅次于降水,其小波系数分别呈正相关和负相关。这可能是由于在平均气温较高的时期,降水增加,更有利于对基流的补给,反之则不然。而最高气温、NDVI 等因素与基流的小波系数相关性较低。说明降水、平均气温、蒸发散为基流周期变化的主导因素,这与基流的趋势变化成因相似。同时,流域内的NDVI 在研究时段内发生了极显著变化,但其对基流的影响不显著,这可能是由于森林植被对基流的作用主要是由其垂直结构所致。
3.2 结论
本文以彭冲涧小流域为对象,基于1983—2017年的基流分割结果,分析了基流的趋势和周期变化规律,并探究了基流的趋势变化和周期变化成因。主要结论如下:
(1)彭冲涧小流域1983—2017年的基流呈非显著下降趋势,年际变化幅度较小;年基流存在3~6年、8~12 年、15~20 年和25~32 年4 种尺度的周期变化,4 个主周期分别为32 年、6 年、10 年和17 年。(2)年基流趋势变化的显著性影响因素为降水、蒸发散和平均气温,三者对基流的相对贡献率大小分别为61.1%、-27.9%、-11.0%。(3)降水为基流周期变化的主导因素,两者具有3 个相同的显著周期,其小波系数相关性(P<0.01)均最高;其次为平均气温和蒸发散,在3~6 年的显著周期上与基流的小波系数相关性(P<0.01)较高。
本文明确了不同显著性影响因素对基流的相对贡献率,并判定了基流周期变化的主导因素。然而,限于试验条件、观测资料等,雨型、雨强、降雨历时、土壤含水量、植被类型等影响因素未进行探讨[40-41],有待于今后进一步研究。

