物联网边缘计算中基于能量感知的动态卸载算法

罗馨玥 李学华* 姚媛媛 岳新伟 云 翔

1(北京信息科技大学信息与通信工程学院 北京 100101) 2(北京佰才邦技术有限公司 北京 100085)

0 引 言

ZK Research的IoT设备发展预测数据显示，到2025年，物联网(Internet of Things,IoT)终端设备的连接将超过800亿[1]。数以亿计的物联网移动设备(Internet of Things Mobile Devices,IMDs)的管理和维护会给设备生产商、运营商带来巨大的成本压力[2]。传统的IoT架构如图1所示，主要分为三层，分别是感知层、传输层和应用层。其中，感知层由传感器和感应器件构成整体感知网络，结合云计算将海量的数据存储到云节点，实现对环境的智能感知及记录。传输层主要负责处理感知层获取的海量信息并上传至应用层。应用层将传输层的信息进行分析并应用于各个领域[3]。传统的IoT架构中感知层获取的海量数据信息，其中一部分是高速率且时延敏感的，由于IoT能够支持和提供的网络带宽、传输时延有限，IMDs的电池容量、节点处理能力受限，因此在基于云计算的IoT架构中引入移动边缘计算(MEC)，将更多的数据计算和存储从“核心”下沉到“边缘”，部署MEC服务器于接近数据源的地方，大大降低传输时延和开销[4]。

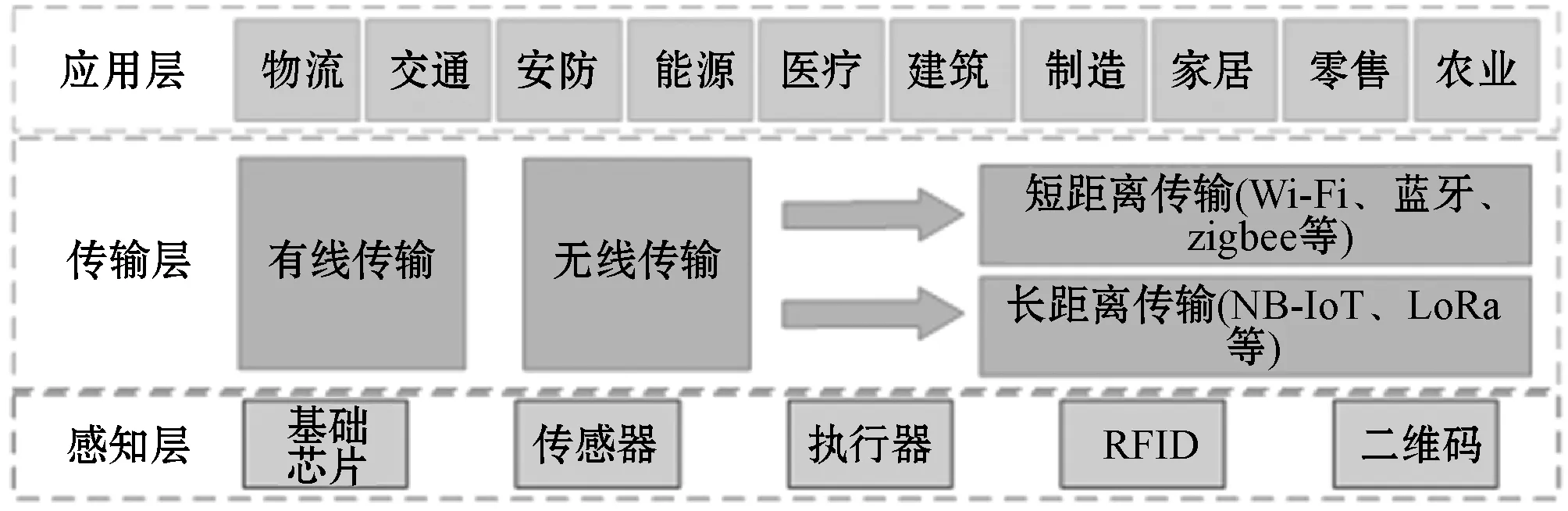
图1 传统IoT架构

计算卸载是MEC中关键技术之一，由终端设备将部分或全部计算任务交给边缘节点处理。计算卸载技术主要包括卸载决策、资源分配和移动性管理三个方面[5]。在多用户的场景中，文献[6]提出了一种计算卸载策略，该策略仅考虑计算资源分配，未涉及无线资源和计算资源联合分配。文献[7]通过控制发射功率和平衡负载，来优化计算资源的分配。文献[8]通过优化带宽分配，在多个设备的MEC系统中获得最优的无线资源分配方案。文献[9]采用最优化算法，通过最佳卸载决策与无线资源分配的共同执行，联合优化系统的时延和能耗。文献[10]采用启发式算法，针对具有多个独立任务的MEC系统共同优化了任务卸载调度和传输功率分配，提高了能量效率。文献[11]提出了一种感知用户移动性管理算法，降低了系统的时延。现有物联网边缘计算中的计算卸载算法主要有最优化算法及启发式算法，以上文献研究的性能指标主要有时延、能耗、吞吐量、发射功率等，而已有研究较少涉及物联网边缘计算中系统能量效率和时延的联合优化。

虽然IMDs卸载高速率计算任务至MEC服务器可以减少处理时延，然而IMDs电池容量有限，可能出现由于电池耗尽中断IMDs数据传输的情况。为了解决上述问题，相关学者将能量收集(Energy Harvest，EH)技术引入到通信系统中，IMDs配备EH装置将收集的可再生能源转换为直流供电，用于实现数据高效传输以及任务卸载，并提出了基于EH技术的计算卸载方法。文献[12]捕获环境可循环利用的能量，如太阳能等，考虑单个移动设备在MEC系统中的计算卸载问题。文献[13]从基站辐射的射频信号中收集能量以用于单个移动设备的任务处理。文献[14]考虑具有EH的D2D辅助MEC系统，提出了一种协同卸载算法，该算法显著提高了平均任务执行成本。文献[15]考虑收集太阳能的单用户MEC系统中计算资源分配问题。文献[16]考虑单个EH设备的MEC系统中平均任务处理时延的优化。

但以上文献考虑的都是单节点应用EH技术的场景，暂未考虑基于EH的多IMDs与MEC系统下平均能效和时延两项性能指标的联合优化。现有算法在多个移动设备的MEC系统中，尚未考虑将移动性管理、卸载决策和资源分配进行联合优化的问题，同时在节点能量资源受限的情况下，未能将系统的能效有效提升。因此本文考虑更切合实际场景的多IMDs随机优化问题。该场景面向高速率IoT业务，多个IMDs配备EH装置捕获环境中的可再生能源转换为直流供电。与传统电池供电的设备相比，卸载决策更加复杂，不仅需要考虑时隙间用户的移动性管理、信道状态信息和电量状态信息，而且考虑在保证系统时延的前提下，提高系统的能量效率。

针对上述问题，本文提出了最大化平均能效算法(MAEE)。该算法首先通过Lyapunov优化将随机优化问题转化为每个时隙内确定性问题。然后为尽可能兼顾系统的时延和能量效率，提出基于贪心的卸载决策算法，在每个时隙内根据设备电池电量和信道状态等因素，分步求解单时隙内最优的卸载决策，当电量充足时引入贪心策略，兼顾系统的时延与能量效率。实验结果表明，与传统算法相比，本文提出的MAEE算法在保证时效性的同时，更大程度地提升了系统能量效率。

1 系统模型

1.1 任务模型

系统模型如图2所示，该系统由多个配备EH装置的IMDs和一个边缘节点组成，其中边缘节点部署于相应的基站上，IMDs可通过连接的基站卸载计算任务至边缘节点。

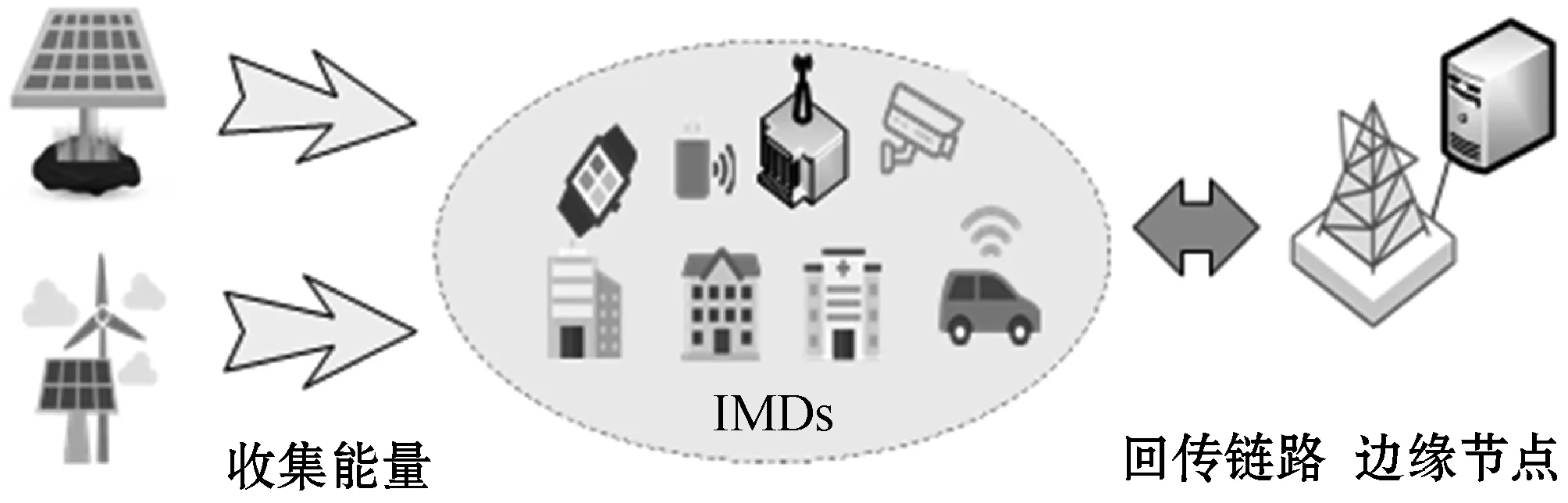
图2 系统模型

(1)

1.2 计算模型

1.2.1卸载计算模型

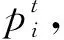
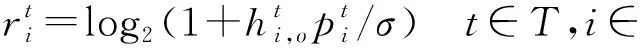
(2)

根据香农公式，单个IMDs执行计算卸载的上行信息速率为：

(3)

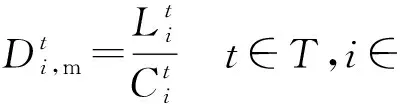
(4)

t时隙所有执行计算卸载的IMDs总时延为：

(5)

t时隙单个IMDs的卸载能耗为：

(6)

因此，t时隙所有执行计算卸载的IMDs总能耗为：

(7)

1.2.2本地计算模型

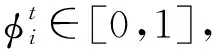
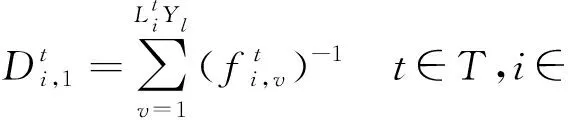
(8)

t时隙所有执行本地计算的IMDs总时延为：

(9)

t时隙单个IMDs的本地计算能耗为:

(10)

因此，t时隙所有执行本地计算的IMDs总能耗为:

(11)

1.3 能量收集(EH)模型

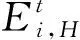
(12)

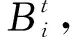
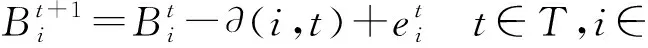
(13)

式中：∂(i，t)为t时隙消耗的电量。

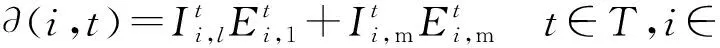
(14)

1.4 系统平均能效

在时隙t内，总的计算量为：

(15)

系统总能耗定义为t时隙内所有IMDs执行任务的能耗之和：

(16)

系统总时延定义为t时隙内所有IMDs执行任务的时延之和：

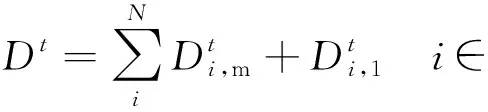
(17)

将能量效率定义为系统总计算量与总能耗的比值，则系统总能效为：

(18)

在最优能量收集的情况下，最大化系统平均能效，故将总的优化问题描述为:

s.t. 式(1),式(3),式(12),式(13)

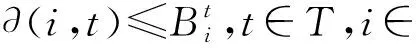
(19)

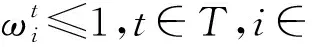
(20)

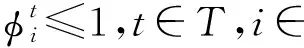
(21)

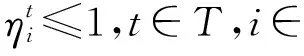
(22)

任务只能由执行本地计算或者卸载计算，用于本地处理的CPU周期频率小于IMDs的最大周期频率，t时隙收集到的能量用于t+1时隙。式(19)是对每个时隙任务处理消耗的电量∂(i，t)的约束；式(20)是对边缘节点的无线资源约束，分配给每个任务的无线资源及分配给所有任务的无线带宽资源不能超过无线上行链路的总带宽；式(21)是对IMDs的无线资源约束，本地计算的CPU周期频率不能超过最大CPU周期频率；式(22)是对边缘节点的计算资源约束，选择卸载执行的IMDs发射功率不能超过最大发射功率，因此联合优化无线资源和计算资源的优化问题为混合整数非线性规划问题。

2 MAEE算法

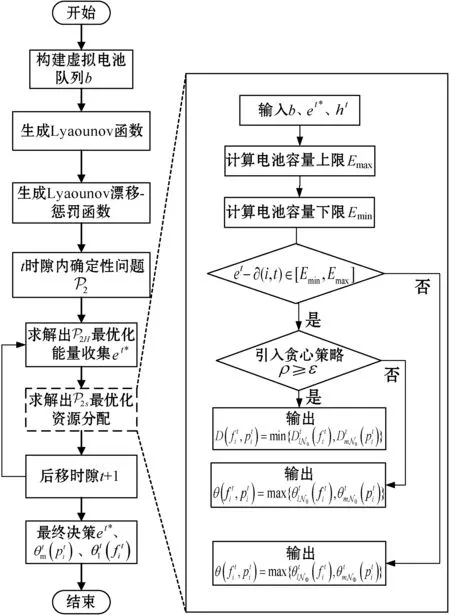
图3 MAEE算法流程

2.1 Lyapunov优化

考虑IMDs初始电量充足的情况，假定CPU周期频率和发射功率仅取决于当前时隙的状态，t时隙内的决定与历史操作无关。Lyapunov优化理论要求目标方程的所有约束都为独立同分布的，由于式(13)和式(14)，t时隙收集的电量用于t+1时隙，导致随机优化问题在不同时隙卸载决策耦合，本文的EH模型不能满足此要求条件，因此Lyapunov优化理论不能直接应用。为了解决该问题，首先在IMDs中引入了扰动参数和虚拟EH队列。

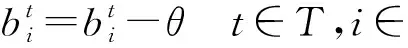
(23)

生成Lyapunov函数：

(24)

Lyapunov漂移-惩罚函数：

ΔV(bt)=Δ(bt)-V·E[θ(t)|bt]t∈T

(25)

s.t. 式(1),式(3),式(12),式(13),式(19)-式(22)

s.t. 式(1),式(3),式(12),式(13),式(19)-式(22)

2.2 基于贪心的卸载决策算法

本文提出基于贪心的启发式算法，在每个时隙内根据设备电池电量和信道状态等因素，分步求解单时隙内最优的卸载决策。当电量不足时，最大化系统能量效率，当电量充足时引入贪心策略，兼顾系统的时延与能量效率。

s.t. 式(1),式(3),式(12),(13),式(19)-式(22)

(26)

(27)

(28)

(29)

(30)

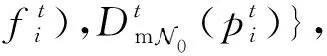
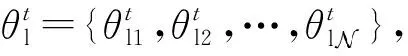
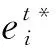
根据以上分析，本文提出的最大化平均能效算法详细求解流程如算法1所示。

算法1最大化平均能效算法

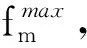
2.接受任务请求，提取请求中任务信息；

3.for eachi∈{1,2,…,N} do；

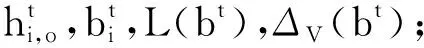
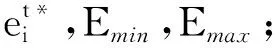
6.引入贪婪策略，求最优的卸载决策

7.Ifet-∂(i,t)∈[Emin,Emax]

8.Ifρ≥ε

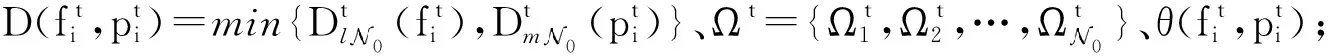
10.Else

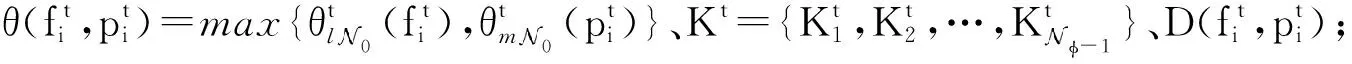
12.Else

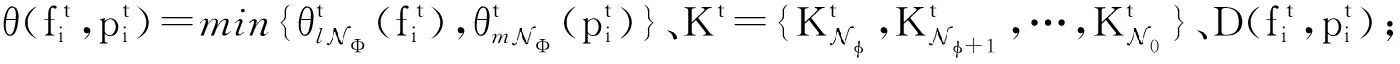
14.End for；

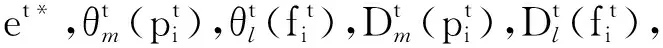
16.t=t+1；

17.End while

3 实验结果与分析

3.1 实验配置

利用MATLAB 2017进行实验验证，实验平台为AMD Ryzen 5 2600CPU 3.4 GHz,8 GB RAM，实验基本参数如表1所示。

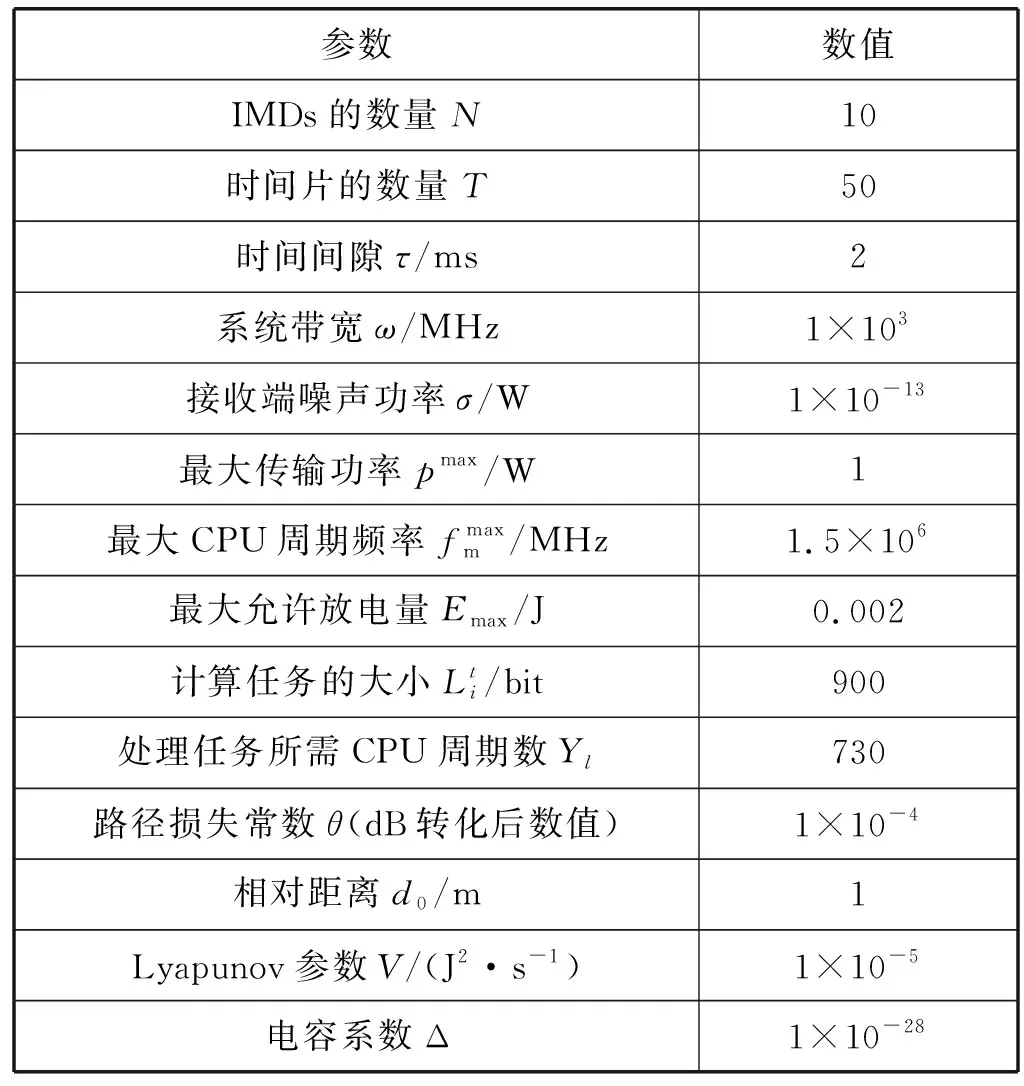
表1 实验基本参数

3.2 结果分析

将本文算法与以下四种算法进行能效比较:

(1) 全部本地处理：该算法仅本地处理所有任务，不进行计算卸载。

(2) 全部卸载处理：该算法仅卸载至MEC服务器处理所有任务，不进行本地处理。

(3) 基于贪心的动态卸载处理：概率为ε时，以最大发射功率pmax卸载处理，概率为1-ε选择时延低的处理模式。

(4) 优化卸载算法(LODCO)[11]：电量充足时，发射功率pt为定值,选择低成本能效处理模式，电量不足时，丢弃任务。

图4为每个IMDs电量水平随时隙变化的情况。每个IMDs的电量在初始阶段不断积累，最终维持在接近满电量的水平上。在当前参数下，每个IMDs的电池电量在第150个时隙后趋于稳定。因为MAEE算法在电池电量不充足时，会选择能效最佳的执行策略，减少每个时隙电池的消耗，从而使电量不断累积增加。当电量稳定趋于满电量时，MAEE算法会兼顾系统时延，会使电量在一定范围内上下波动。

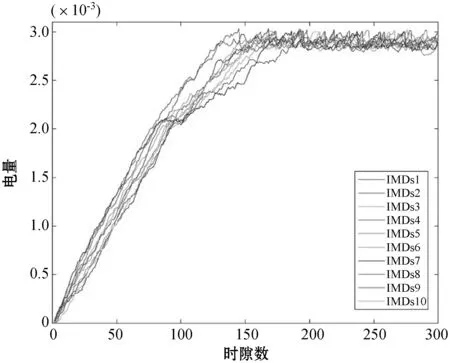
图4 多个IMDs电量随着时隙变化的曲线图

3.2.1时延性能比较

图5展现的是系统平均时延随着贪心系数ε的变化趋势。在电量充足时，不同的贪心系数会对算法的决策造成影响，从而影响系统的时延。在贪心系数较小接近于0时，系统选择时延最佳模式的概率低，导致系统时延较高；随着贪心系数的增大，系统以更大的比例选择时延最佳的执行模式,且可以看出贪心系数为0.7之后，时延的减少逐渐放缓，趋于稳定。

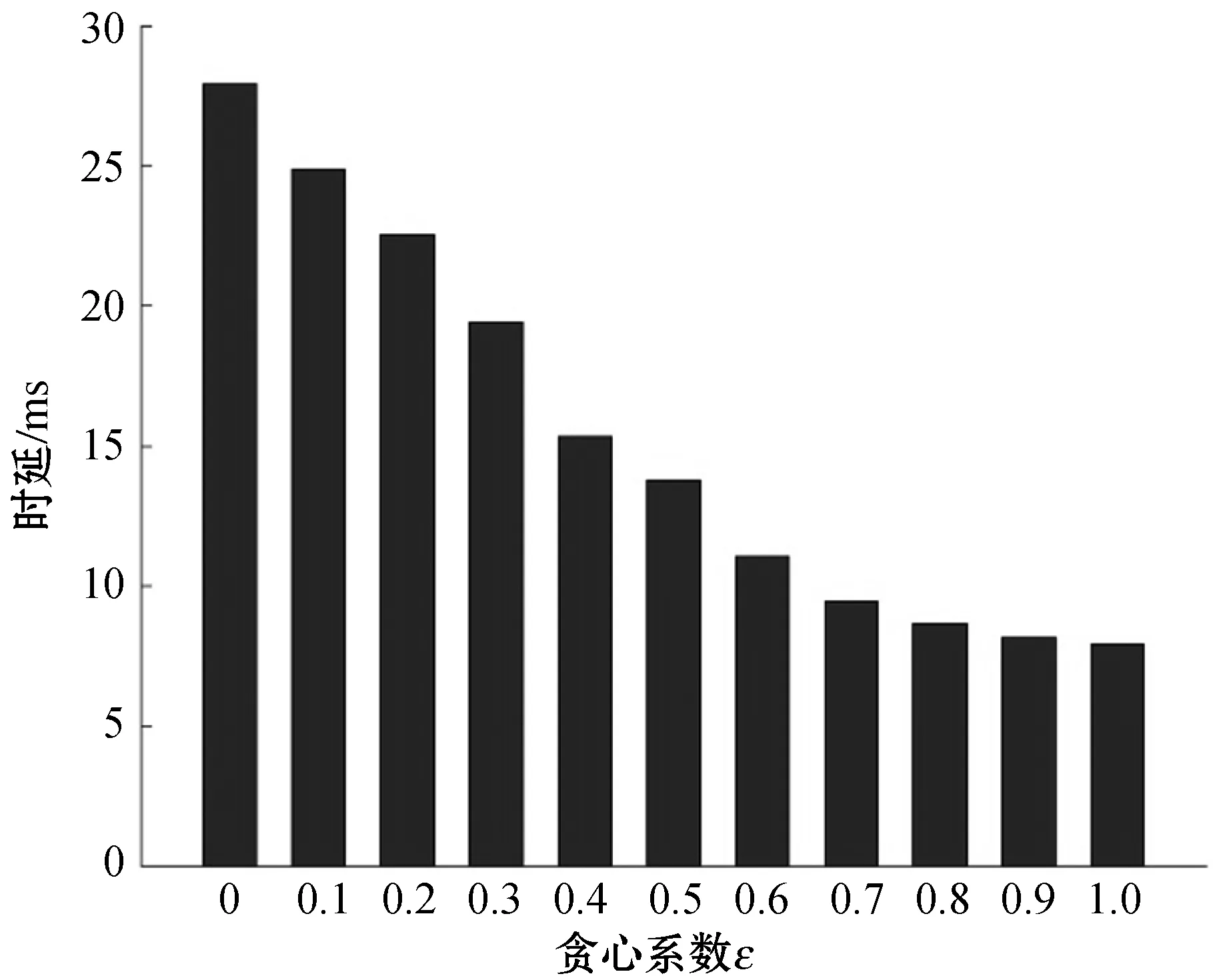
图5 贪心系数ε对时延的影响

时延随时隙变化关系如图6所示。由于本地处理的计算资源匮乏，与边缘节点的计算资源有较大差距，因此全部本地处理的时延较大。全部卸载处理虽然可以利用MEC服务器计算资源快速处理任务，但是由于IMDs会在一定区域内移动，使卸载任务至边缘节点的时间产生变化，导致时延在一定范围内上下波动。基于贪心的动态处理算法未能很好地优化时延因素。LODCO算法主要考虑对时延的优化，因此其在时延的表现上较好。MAEE算法在初始阶段任务处理时延略大，随着时间的推移，时延逐渐下降。这是因为MAEE算法在初期电量不足时主要选择能效最大化的执行策略，未考虑对时延的优化，而随着时间推移，当电量充足时MAEE算法开始兼顾时延，使后段的时延逐渐下降。

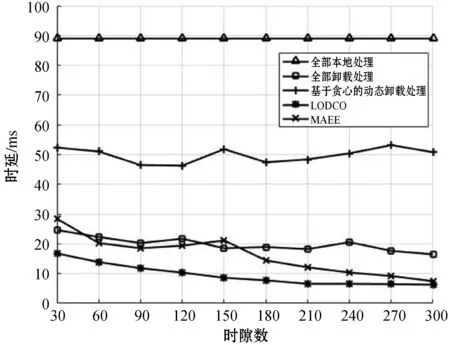
图6 时隙数对时延的影响

3.2.2能效性能比较

系统能量效率随时隙变化关系如图7所示，数据量设置为500 bit。全部本地处理时需要过多的本地CPU资源计算，导致能量效率较低。全部卸载处理时，仅需考虑任务卸载能耗，从而大大提升了能量效率，但考虑到任务卸载距离的变化，其能效表现会有一定的浮动。LODCO和贪心算法会在卸载率和时延等因素上有所取舍，因此能效表现略差。MAEE算法在初期电量不足时会选择能效最大化的策略，使其电量得到充分的利用，且随着电量的不断增加，其可处理的任务数量也会增加，从而提升了能量效率。当电量积累到一定程度后，MAEE算法会在能效和时延之间进行权衡，导致能效有一定程度的降低。

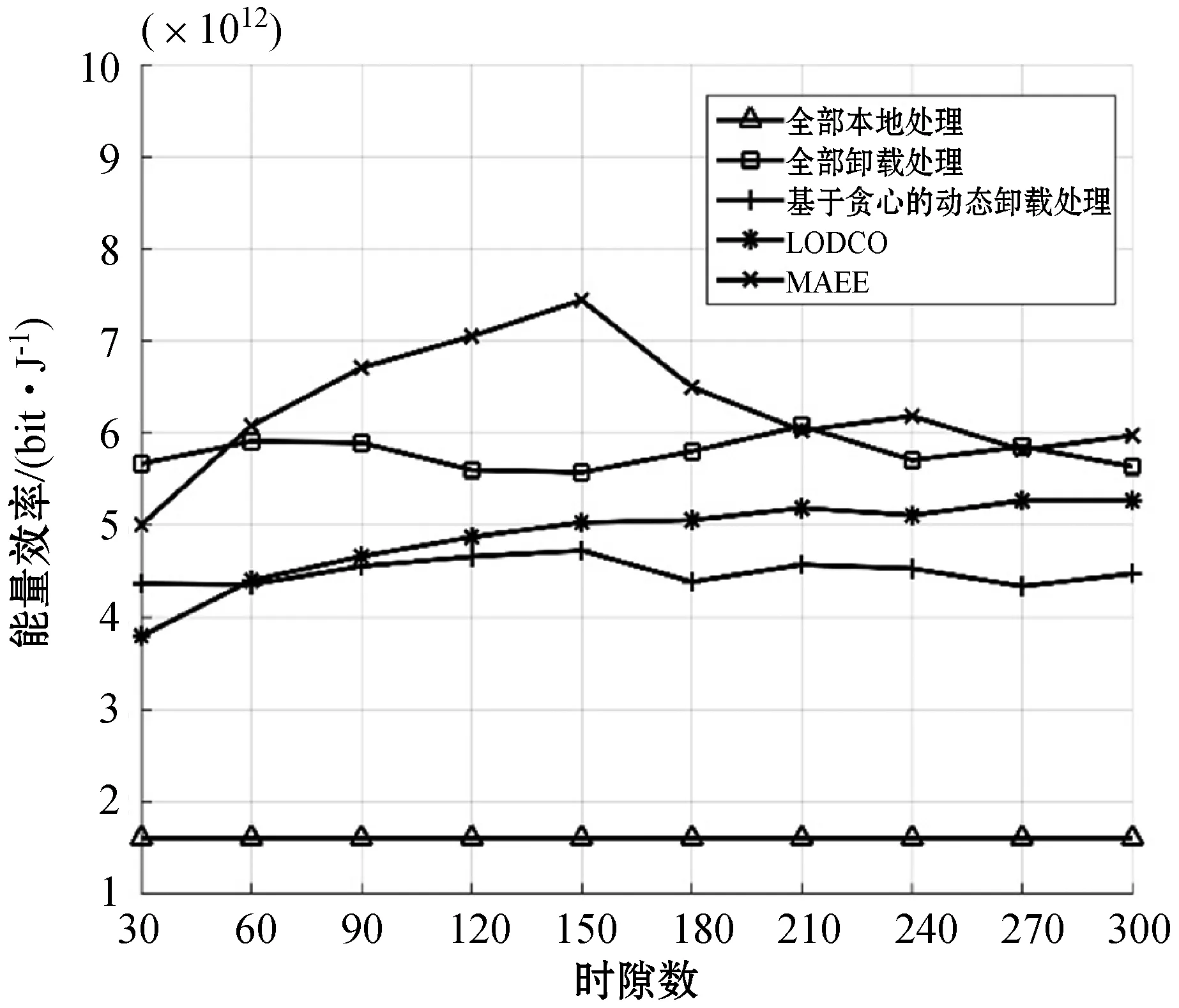
图7 时隙数对平均能量效率的影响

图8展现的是系统能量效率随着计算数据量变化的关系。全部本地处理算法在任务数据量低的时候能量效率较高，实验结果表明对于小数据量任务，本地处理比卸载处理消耗的能量少，而随着数据量的增加，本地处理的能耗呈指数型增加，因此其能效逐渐降低。全部卸载处理算法能耗仅在任务传输上，在小数据量时优势不明显，但随着数据量的增长，其仍可使用较少的能量卸载任务，从而使能量效率不断提升。基于贪心的动态卸载算法和LODCO算法在卸载率和时延等因素上各有取舍，但在能效的优化上不佳。本文提出的MAEE算法根据图4可分为两个阶段，在前150个时隙内，由于电量不足MAEE算法将选择能效最大的方案，因此其能效表现最好，而当电量充足时会在能效和时延之间进行权衡，因此能效略有降低，但仍然保持在较高的水平上。

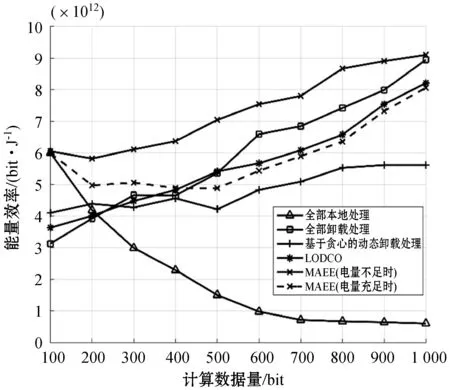
图8 计算数据量对平均能量效率的影响

4 结 语

本文研究了MEC中多个IMDs之间的移动性管理、能量收集、卸载决策和资源分配的联合优化问题，提出一种最大化平均能效算法，即MAEE算法。该算法联合统筹无线资源和计算资源分配，针对不同环境自适应地进行卸载决策，在降低系统时延的同时，最大化系统能量效率。实验结果表明，在多IMDs和大数据量任务的复杂环境中该算法能够显著提升能效，并降低任务处理时延。