基于PLS的多维力传感器动态力反演研究
董建平 周兴林 朱 攀
(武汉科技大学机械自动化学院 湖北 武汉 430081)
0 引 言
传感器的被测量是通过测量信号的反演得到的。工业测试中静态或准静态力测量技术较为成熟,而关于动态测量技术的研究尚不完善[1]。动态测量时被测量是与时间强相关的,利用静态的测量方法得到的结果不准确[2]。
另外,根据测力分量数目的不同,传感器可以分为单维、多维。多维力传感器主要用于力与位置精密控制领域,如在汽车轮胎接触应力测试[3]、机械装置[4]、医疗器械和机器人技术[5]等方面,其在精密测控领域是不可或缺的。
实现多维力传感器动态测量需要经过动态标定和反演,反演是本文关注的重点。由于设计、制造和安装方面的限制,多维力传感器的弹性体(敏感元件)往往为一体化结构,因此各维测力方向上会产生干扰,即存在维间耦合,这严重影响了传感器的测量精度,减轻或消除维间耦合是多维力传感器测量中急需解决的问题。目前学界存在两种解决思路,其一是从结构上消除耦合误差[6],这对传感器的制造和安装精度要求较高;其二是设计解耦系统,采用解耦算法减轻耦合误差的影响,提高测量精度[7-8]。
实际测量中,数据都是带有噪声的,解算出的输入力与真实力之间存在偏差,多维力传感器的动态力反演需要减小耦合误差,据此,国内外学者做了一系列研究。徐科军等[9]针对腕力传感器提出了不变性解耦,采用解耦网络实现解耦模型的降阶,通过简化运算减小误差,取得了良好效果。但这种方法有较大的限制性,对于非最小相位系统需要考虑模型的稳定性。同年,徐科军等[10]进一步提出迭代动态解耦方法,对不变性动态解耦方法进行优化,能够较好地减轻耦合影响,但在求解高阶复杂系统时,构建解耦网络结构十分困难。宋国民等[11]将传感器的传递函数转化为对角优势矩阵,从而弱化维间耦合的影响,实现近似解耦。夏秋等[12]提出了基于独立成分分析(ICA)的多维力传感器解耦方法,表示经过独立成分分析,传感器的测量效果优于对角优势化补偿方法,能有效提高传感器的测量精度。国外关于动态反演的研究大多是采用滤波器。Eichstädt等[13]根据补偿滤波器的设计方法把数字反卷积滤波器分为FIR滤波器和IIR滤波器,以此来削弱噪声影响。瑞典学者Hessling[14]根据测量系统有理传递函数模型和数字滤波器模型得到被测量。
本文采用偏最小二乘法(Partial Least Squares,PLS)对被测量进行反演,通过交叉验证选取参数,利用均方差筛选主成分,从而减轻测量噪声的影响,设计的两个仿真算例表明,该方法能有效减轻噪声影响,提高测量精度,且解算过程稳定有效。
1 多维力传感器反演模型
多维力传感器的敏感元件工作在线性区域,在线性时不变(LTI)条件下,传感器测量系统可看作多输入多输出系统(MIMO)。线性时不变条件下的输入输出可以表示为卷积关系:
(1)
式中:hji(t)hji(t)表示从第i个输入到第j个输出uj(t)通道的冲激响应函数,其中有i=0,1,…,p,并且j=0,1,…,q。
其矩阵表达形式为:
(2)
式中:uj为第j个输出的向量形式;fi为第i个输入的向量形式;Hji为与hji(t)相对应的冲激响应核函数矩阵。
假设多维力传感器系统输入和输出分别为f和u:
f=[f1,f2,…,fp]T
(3)
u=[u1,u2,…,uq]T
(4)
动态特性矩阵用H来表示:
(5)
MIMO系统可表示为:
u=Hf
(6)
上述方程的求解通常是不适定的,对测量过程中的扰动十分敏感,求解过程中容易出现矩阵的病态问题。为避免求解的病态问题,可将传感器的动态力反演看作作用位置已知的载荷识别问题,对传感器输入量的反演即为模型的系数辨识。
可采用建立回归模型,将输入量f作为传感器系统的参数进行识别的方法来获得输入信号的近似解,通过优化使其可以表达真实信号的特征,具有更好的稳定性。
2 偏最小二乘算法
偏最小二乘(Partial Least Squares,PLS)是一种利用潜在变量对观测变量集之间的关系进行建模的广泛方法。它包括回归和分类任务以及降维技术和建模工具。所有偏最小二乘方法的基本假设是,观测数据是由一个系统或过程产生的,该系统或过程是由少量潜在(非直接观测或测量)变量驱动的。利用PLS将观测到的数据投影到其潜在结构中是建模的核心[15]。将PLS用于求解式(6),当u为一维变量时,PLS可以视为一个正则化的最小二乘拟合[15]。
PLS与其他方法的不同之处在于PLS对XYT进行特征值分解,适用于解决变量之间的共线性较高的情况。PLS将原始数据投射到更紧凑的潜在变量空间中,能够分析单个变量的重要性,建立自变量与因变量之间的关系,删除影响较小的变量,使模型包含最少的变量数,以此来实现弱化噪声影响的目的。且计算和执行简单,具有较好的稳定性[16]。
2.1 算法原理
分别从自变量集合X和因变量集合Y中提取成分t1和u1,使得t1和u1尽可能多地表达它们各自的数据信息,并且t1与u1和X与Y的相关系数取到最大值,将X与Y提取成分后的残余信息作为新的集合来提取t2和u2。对上述过程进行迭代,直到满足精度要求。经过主要成分信息的提取,将次要信息去除,可最大程度地减轻或消除噪声影响,提高传感器的测量精度。
2.2 算法实现步骤
本文将PLS方法用于多维力传感器的动态反演,建立一个单变量的偏最小二乘回归模型(记为PLS1[16]),下面是PLS1的建模方法。
2.2.1第一、二成分选择
将数据进行处理(减去均值、除以标准差)获得新的X和Y。分别从X和Y中选择第一成分t1和u1。
t1=Xp1
(7)
u1=Yq1
(8)

提取出的成分t1和u1要最大程度地包含X和Y中的变异信息,且t1对u1有最大的解释能力[17],即要求Cov(t1,u1)达到最大。
分别求取XTYYTX和YTXXTY最大特征值对应的特征向量即可得p1和q1,从而可得成分t1,本文中q1=1,u1=Y。分别建立回归方程有:
(9)

分别以残差矩阵X1和Y1作为新的X和Y,用上面的方法求得第二成分t2。求取新的特征矩阵对应的特征向量p2,则:
t2=X1p2
(10)
建立X1和Y1对t2的回归方程,有:
(11)

2.2.2原始数据系数计算
同以上方法,可对第h成分th进行提取。h可采用交叉验证估计均方误差的方法获得。由上述方法不断计算可得:
(12)
式中:E和F是残差矩阵[18]。
式(12)的矩阵形式如下:
(13)
式(13)即为Y关于X的回归方程,其中系数B=PRT。在算法计算过程中收集P和R的值就可以得到原始矩阵的系数,从而实现输入量的反演。
2.3 交叉验证
在通过偏最小二乘法建立模型时,成分参数的选择尤为重要,若h值选择过小,则不足以较为完整的表达数据信息;若h值选择过大,则会代入噪声信息。本文采用十折交叉验证(10-fold cross validation)的方法选取参数,方法如下:
将数据分为十等份,取出其中一份作为测试数据,其余九份数据作为训练数据,每次选择不同份的数据作为测试数据,交叉验证重复十次,并将十次交叉验证过程中训练数据对测试数据的识别准确率作为结果。
这种方法的优点在于,保证每个子集都参与训练且都被测试,有效降低泛化误差。本文通过十折交叉验证估计均方根误差,选取均方根误差最小的参数作为选取的成分数。
通过估计均方根误差(Root Mean Square Error,RMSE)的方法选择最佳的成分数目h。均方根误差用以评价数据的拟合状况,它的值越小,表明预测模型与真实模型的拟合程度越高,RMSE定义为:
(14)
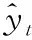
衡量模型是否适合训练数据的指标R2定义为:
(15)
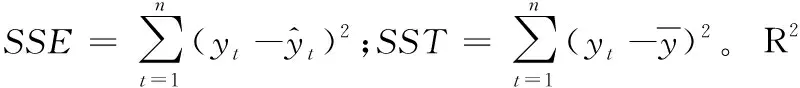
3 仿真验证
通过仿真分析对本文提出的方法进行有效性验证。多维力传感器的两两通道间存在干扰,以文献[9]中一个二输入二输出系统为例进行仿真分析,其传递函数模型为:
(16)
3.1 矩形脉冲动态力输入信号
为了验证PLS算法的有效性,将两个矩形脉冲信号作为多维力传感器的动态力输入,如图1所示,矩形脉冲信号具有非常丰富的频率信息,能够十分有效地验证算法的优化效果,得到的输出信号如图2所示。为输出信号添加SNR为10 dB的高斯白噪声,如图3所示。

图1 矩形脉冲动态力输入信号

图2 矩形脉冲信号的传感器输出信号
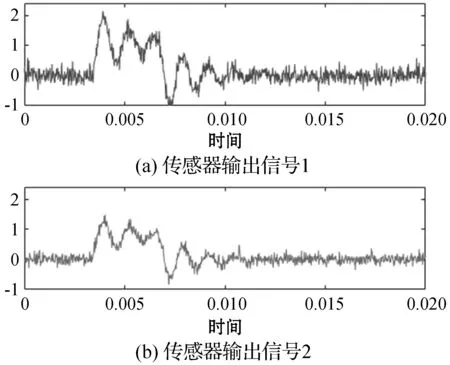
图3 添加噪声后的输出信号
若不进行处理,直接通过输出信号反演输入信号,输入信号发生失真,得到的结果是无意义的,如图4所示。

图4 直接反演求解的输入信号
根据2.2节所述步骤,利用PLS算法来实现传感器动态力的重建,可通过交叉验证估计均方根误差的方法确定提取的成分数量h,如图5所示。可以看出,随着成分数的增加,均方差逐渐减小,从第四个成分数开始逐渐变缓,在h=6处均方差基本达到最小,满足参数要求,仿真结果如图6所示。

图5 交叉验证选取成分数

图6 重建信号与真实信号对比
从PLS求解值与真实值的对比结果中可以看出,通过PLS算法得到的曲线与真实值趋势一致,围绕真实值上下轻微波动,这是由于矩形脉冲信号包含丰富的频率信息。相较于直接根据测量值反演被测量的结果,该方法具有明显的优势,求解值能够有效表达真实值。
3.2 双半正弦信号输入
将双半正弦信号作为传感器的输入信号,进一步验证PLS算法的有效性。如图7所示,分别以两个双半正弦信号作为输入信号。

图7 双半正弦输入信号
为输出信号添加信噪比为10 dB的高斯白噪声(图8),由文中2.3节所述,利用十折交叉验证估计均方差,选取最小值以确保数据保留较高精度,如图9所示,从h为3时均方根误差变化较为平缓,当h=5时均方根误差基本达到最小值,故选取参数为5既能表达大部分信息,又可避免噪声的影响。通过重建得到的输入信号与真实值对比结果如图10所示,可以看出,PLS求解值能有效地表示真实值的特征。
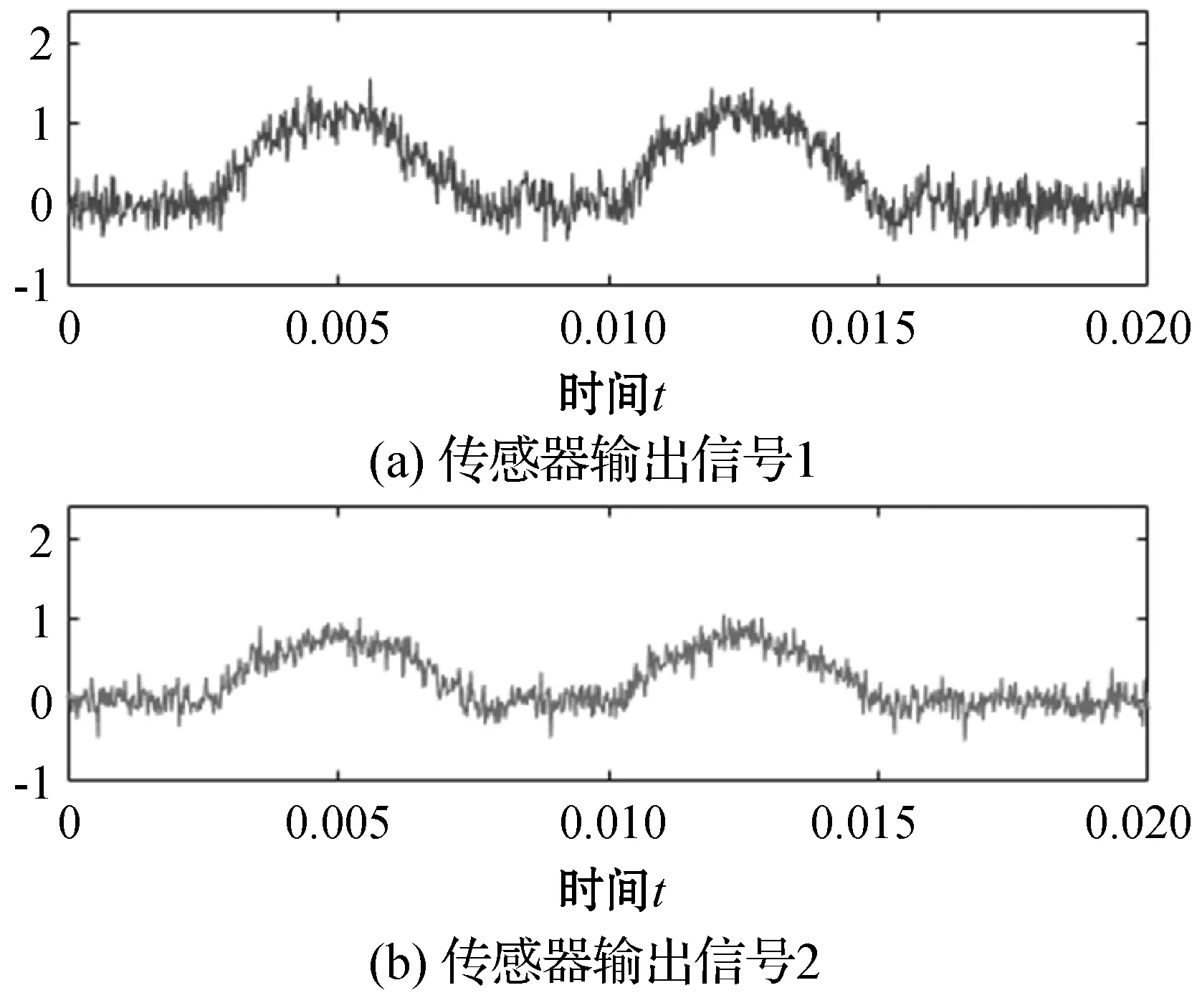
图8 添加噪声后的输出信号
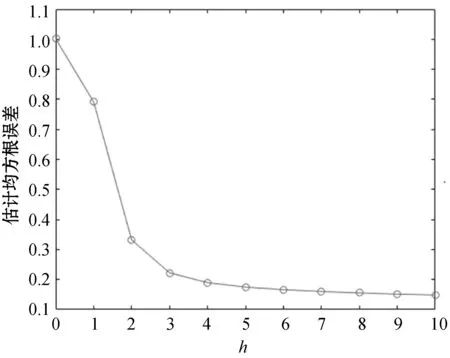
图9 交叉验证选取成分数

图10 重建信号与真实信号对比
3.3 PLS算法与PCA算法的比较
与PLS算法类似,主成分分析(Principal Component Analysis,PCA)也是一种常用的降维去噪方法,因此PCA也可以用于多维力传感器的动态反演,这里把PCA算法与PLS算法得到的反演结果进行比较。
同样采用式(16)的传递函数模型进行仿真,分别利用3.1节的矩形脉冲信号和3.2节的双半正弦信号作为输入,为输出信号添加信噪比为10 dB的高斯白噪声后,通过PCA降噪实现传感器的动态反演,得到的PCA求解值与真实输入信号的对比如图11和图12所示。

图11 两种算法的矩形脉冲信号求解结果对比

图12 两种算法的双半正弦信号求解结果对比
可以看出,采用PCA实现多维力传感器的动态反演有一定的效果,但相较于PLS的求解效果反演精度不高,与真实值的偏离程度较大。原因是PCA降维过程中,因变量并没有参与主成分的构造,所以PCA无法保证同时指导预测自变量的方向和预测因变量。但PLS算法不仅能很好地概括自变量的信息,而且对因变量也有很强的解释能力。
4 结 语
本文针对多维力传感器在先验信息缺乏时的动态反演出现信号失真的问题,提出通过PLS算法提取有效成分来降低噪声对测量结果的影响。相较于传统求解过程中的矩阵病态问题,求解过程更加稳定。采用交叉验证估计均方差的方法选取参数,既保证了信息的完整性,又在最大程度上摒除噪声信息,保证求解精度。仿真结果表明,在受到信噪比为10 dB的高斯白噪声影响时,采用PLS方法依然能较准确地还原矩形脉冲和双半正弦脉冲,表明该方法的可行性和有效性。PLS通过对数据的处理实现传感器的动态反演,相较于矩阵求解法更加稳健,抗干扰能力更强,甚至在与PCA方法的比较中也表现出更好的鲁棒性。

