郑西高铁地面振动实测分析及隔振沟效果研究

宋玉兰，杨立中

（西南交通大学地球科学与环境工程学院, 四川 成都 610031）

随着我国高速铁路线网的加密及列车运行速度的大幅提升，高铁列车动载引起的环境振动问题越来越普遍[1−2]。近年来，生活水平的提高使得人们对环境舒适度要求越来越高，研究人员也逐渐关注列车振动对环境的影响，并把振动列为七大环境公害之一[3−4]。高铁列车运行引起的振动会影响沿线居民的正常生活和精密仪器的使用。因此，研究高铁列车运行引起的振动沿时间和空间的衰减规律及减振措施具有重要的意义。

高速列车引起的地面振动问题十分复杂，轮轨接触关系、轨道不平顺、土体材料属性、车辆-轨道-基础-土体动力特性及相互作用关系等均会对其产生影响。因此，众多学者将现场测试视为重要的研究手段，为理论分析、预测提供有效的实测数据验证[5−7]。高广运等[8]对秦沈铁路车致地面振动进行了实测分析。李小珍等[9−10]发现近场测点的加速度时程呈现出明显的列车周期性加载现象。马骙骙等[11]分析了宝兰客专路堤段不同类型车致地面振动在黄土中的衰减规律。何鉴辞等[12]研究了某高速铁路高架线路直线与曲线段环境振动的差异。翟婉明等[13]研究了软土地基上车致地面振动问题。董海山等[14]通过测试数据的回归分析，得到了高铁桥梁段车致地面振动衰减经验公式。从以上的环境振动研究可以看出，现有的研究大多单独针对高铁路堤段和高架段进行振动理论及现场实测的分析，缺少二者的对比分析。现有文献中只有毛昆明等[15]对比了沪宁城际CRH动车组运行引起的高架段和路堤段的地面振动竖向速度，得到了一些有重要参考价值的结论。因此有必要从环境振动的角度比较高架桥段与路堤段车致地面振动的差异性。

随着高铁振动问题的日益突出，减振措施也相应出现。最简单有效的方法就是在线路附近开挖一条平行于线路的沟槽以切断振动的传播路径或使振动发生散射和衍射，从而降低沟后建（构）筑物的振动响应[16]。由于空沟良好的隔振效果，现有对隔振沟的研究主要集中在对振动衰减有影响的空沟位置、几何尺寸等方面，对填充沟的研究较少。巴振宁等[17]研究了层状饱和地基中空沟的隔振性能；张立群等[18]进行了空沟减隔振措施的室内模型试验；曹志刚等[19]运用饱和半空间模型研究隔振效果。黄土作为一种具有大孔隙和湿陷性的特殊土壤，在世界范围内广泛分布[20−21]。黄土的特殊性质使其对高速铁路振动传播的影响不同于其他土层。目前，对黄土地区高速铁路隔振沟的研究还相对较少。

本文通过对郑西高铁高架段和路堤段的现场测试，对比分析了高架段和路堤段地面振动特征及其传播的衰减规律。引入无限元-黏弹性边界条件，建立考虑隔振沟的三维数值模型，分析了高铁路堤段空沟及填充沟的减隔振效果差异，以期为高速铁路两侧环境振动的控制提供参考。

1 环境振动测试

郑州——西安高速铁路客运专线（简称郑西高铁）是我国“八纵八横”高速铁路网的重要组成部分，沿线80%区段为黄土覆盖。测试场地选取在郑西高铁K1042+200附近路堤段和K988+848附近高架段。轨道结构均为CRTSⅡ型双块式无砟轨道。轨枕为钢筋桁架连接的双块式轨枕。

测试场区自上而下地层岩性分别为：第四系上更新统自重湿陷性黄土约19 m，上更新统非湿陷性黄土约28 m，中更新统砂层。地层岩性稳定。测试场区地下水为第四系孔隙潜水，埋深约30 m。

测区场地开阔，地势平缓，周围为大片农田，无建筑物，不受其他交通振动的影响，便于布设测点，测试条件较好，便于单独分析列车引起的地面振动效应，如图1所示。

图1 测试场区Fig.1 Test site area

测试仪器采用中地装（重庆）地质仪器有限公司生产的三分量EPS便携式数字地震仪（图2）。

图2 EPS便携式数字地震仪Fig.2 EPS portable digital seismograph

本次测试测点选取在区间直线段，测试区段前后200 m范围内钢轨需无明显波形磨耗，轨道无病害。在垂直线路方向上，每隔15 m布置一个测点，测线总长180 m，仪器编号依次为1～12，布置过程中保证传感器底部与地面紧密接触。测点布置见图3。

图3 测点布置图Fig.3 Layout of the measuring points

郑西高铁运营的动车组为“和谐号”CRH2C型高速动车组。测试列车的特征长度见图4。典型车速下列车几何特征频率见表1。

图4 测试列车的特征长度Fig.4 Characteristic length of the train

表1 典型车速下列车几何特征频率Table 1 Geometrical characteristic frequencies of the train at typical speeds

2 高架段与路堤段振动特性实测对比

现场通过记录列车通过测段的时间计算列车运行速度。试验较完整地采集到150，200，240，250，300 km/h等运行速度下高架段与路堤段不同测点的竖向振动加速度。数据处理前均进行了滤波，仅保留85 Hz以下的振动。本文主要以列车运行速度240 km/h为例进行分析。

2.1 位移时程和衰减特征分析

地面竖向位移时程关系和峰值位移衰减情况见图5和图6。从图5可以看出，越靠近轨道，地面振动越明显，且高架段和路堤段均未出现明显的轮对产生的周期性峰值，可能的原因是黄土的结构性和非均质性，在不同介质传播过程中振动产生了叠加效应。从图6可以看出，随着距离的增加，位移峰值逐渐衰减。

图5 位移时程曲线Fig.5 Displacement-time curves

图6 位移峰值衰减曲线Fig.6 Displacement peak attenuation curves

高架段和路堤段的振动衰减特性明显不同。整体上看，路基段的振动响应大于高架段。从紧临线路的测点1至距线路30 m的测点2，高架段振动位移峰值由 0.26×10−4m 迅速衰减至 0.16×10−4m，衰减率达到38.5%；路堤段振动位移峰值由0.37×10−4m迅速衰减至0.31×10−4m，衰减率达到16.2%，即高架段近场区域衰减作用高于路堤段近场区域。

对于高架段，距线路30 m范围内为振动快速衰减区，当距离大于30 m位移衰减的速度明显降低，但是在45，90 m处出现反弹增大现象；对于路堤段，距线路75 m范围内为振动快速衰减区，并且在60，120 m处出现反弹增大现象。随着距离的增加，两者的位移峰值逐渐趋于一致。由于测线较长，本次测试发现了2 次反弹增大现象。对于反弹增大现象，李小珍等[10]研究认为是由于振动波在基岩与地表土层间多次反射所致，与多种原因有关。关于反弹增大原因尚待进一步研究。

路堤段地面振动反弹增大位置滞后于高架段。高架段在45 m处出现第一次反弹增大，相较于前一测点的增大率（本文定义为一次反弹增大率）为3.15%；在90 m处出现第二次反弹增大，相较于前一测点的增大率（本文定义为二次反弹增大率）为18.70%。路堤段在60 m处出现第一次反弹增大，一次反弹增大率为0.75%；在120 m处出现第二次反弹增大，二次反弹增大率为21.48%。通过分析发现，高架段和路堤段的二次反弹增大率均明显大于一次反弹增大率。

2.2 地面振动频谱分析

通过傅立叶变换得到的地面各测点的频谱如图7所示。从频谱结果可以看出，地面振动波的频率主要分布在60 Hz以下。随着距离的增大，高频迅速衰减。远距离处频谱主要由低频控制，主要分布在10 Hz左右。

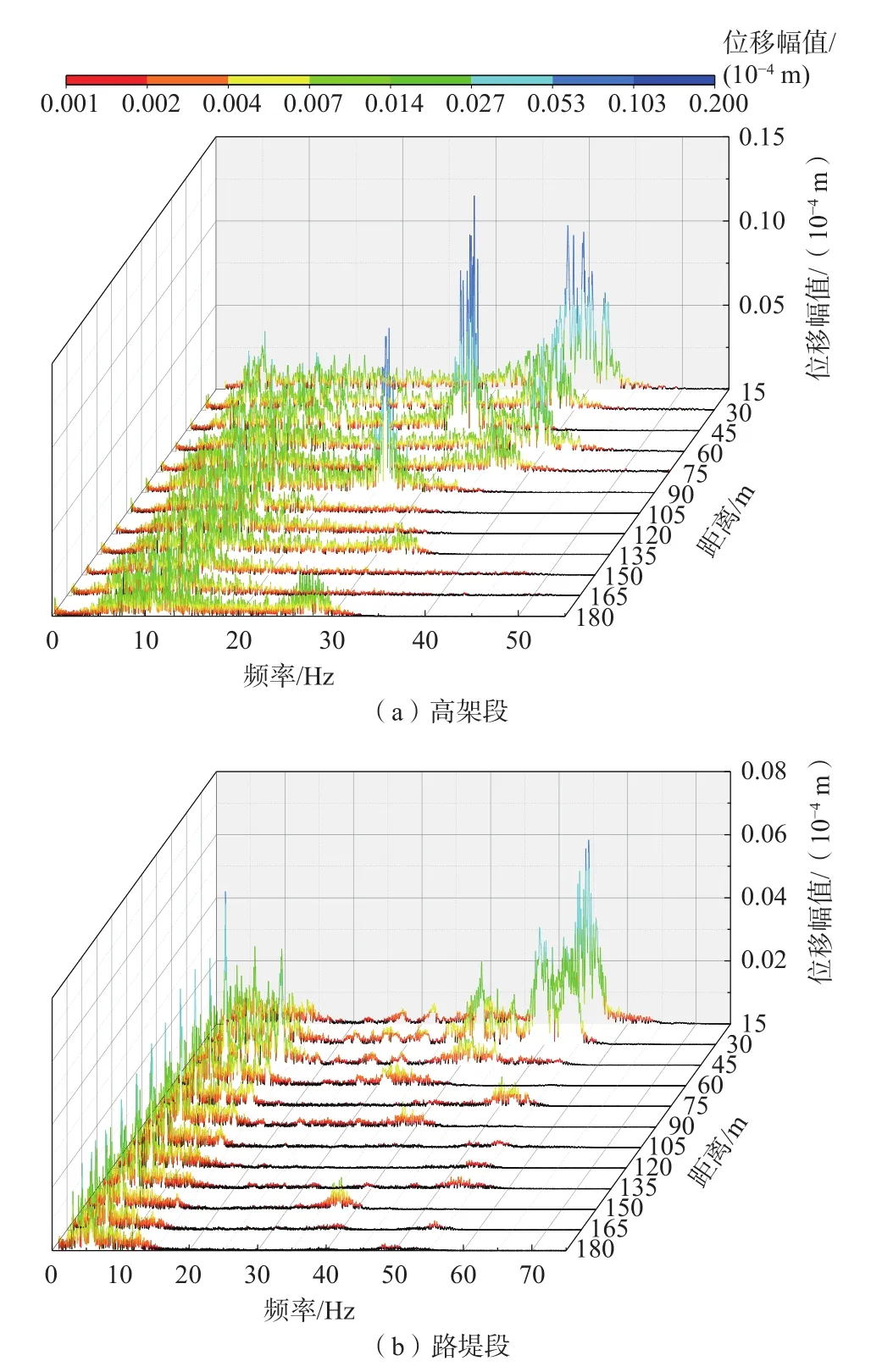
图7 位移频谱曲线Fig.7 Displacement spectrum curves

列车运行时，列车特征频率会对轨道结构产生脉冲激励，使得频谱曲线上在列车特征频率附近出现峰值。当距线路较近时，固定轴距激励频率（f1）、车辆定距激励频率（f2）、前后车相邻转向架中心距激励频率（f3）和车长激励频率（f4）均对地面振动产生重要的影响。随着距离的增加，车辆定距激励频率（f2）和车长激励频率（f4）对频率幅值的影响减弱，这主要受到土体固有频率的截止作用。当距离较远时，固定轴距激励频率（f1）、前后车相邻转向架中心距激励频率（f3）及其倍频对位移幅值起主要控制作用。

高架段和路堤段的频谱曲线呈现较大的差异性。相较于路堤段，高架段的地面振动频率分布范围较宽，频率分布也较连续。高架段的地面振动频率主要分布在5～45 Hz，路堤段的地面振动频率主要分布在0～20 Hz和距离线路较近时的40～60 Hz。高架段的高频部分主要分布在距线路75 m范围内，路堤段的高频部分主要分布在距线路45 m范围内，且高架段的峰值频率低于路堤段。

2.3 环境振动评价

20世纪80年代颁布执行《城市区域环境振动标准》（GB 10070——88）[22]。该标准中环境振动标准值见表2。

表2 城市各类区域Z振级标准值[22]Table 2 Standard values of Z vibration level in various urban areas[22]

为了与标准进行比较，需要将测试数据转化为加速度振级。加速度振级具体计算公式如下：

（1）采用不计权的方式，计算得到各测点的垂向振动加速度级（VAL）：

式中：arms——振动加速度有效值/（m·s−2）；

a0——基准加速度/（m·s−2），取 1×10−6m/s2。

（2）按照 ISO 2631/1——1997 国际标准规定的全身铅垂向振动不同频率计权因子计算得到地面振动Z计权振动加速度级（VLz）：

T——振动测量的平均时间/s；

aw——经过频率记权的加速度/（m·s−2）。

计算结果表明各测点Z振级均小于80 dB（图8），满足规范中对于铁路干线两侧环境振动标准的规定。高架段30 m外满足工业集中区、混合区、商业中心区、居民、文教区的要求，60 m外满足特殊住宅区的要求。路基段60 m外满足工业集中区、混合区、商业中心区、居民、文教区的要求，90 m外满足特殊住宅区的要求。同时可以看出，高架段和桥梁段Z振级与位移峰值随距离衰减的规律基本一致。列车运行引起的Z振级沿测线方向整体呈现衰减趋势。路堤段环境振动高于高架段1～7 dB。

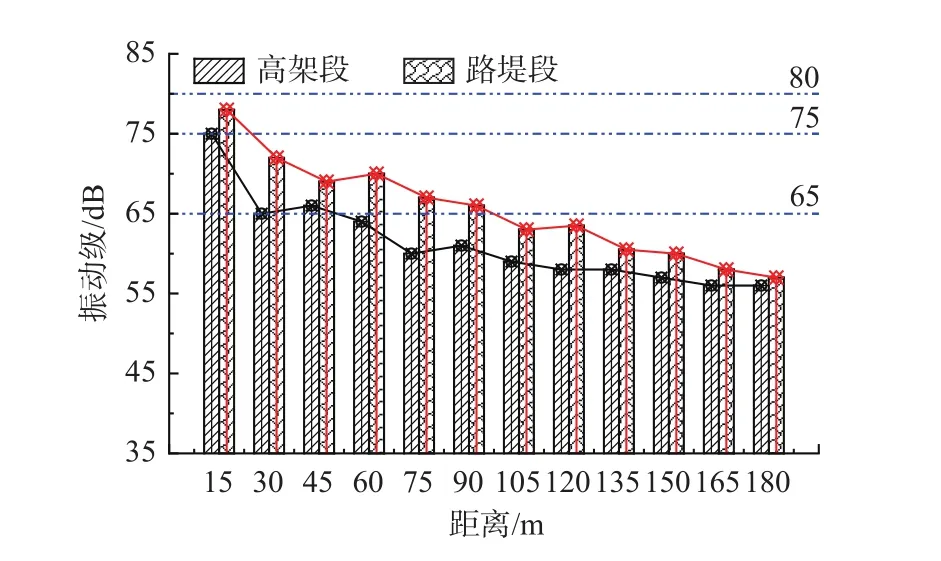
图8 各测点Z计权振级衰减曲线Fig.8 Z-weighted vertical ground vibration levels attenuation curve of each measuring point.

目前我国对铁路环境振动的评价均参考20世纪80年代的标准，该标准基于我国当时的铁路状况制订，未将高速铁路考虑在内。现阶段我国还没有一个针对于高速铁路的环境振动标准。截至2021年底，我国高铁运营里程突破4×104km。同时，人们对环境舒适度要求越来越高。显然，旧规范已不再适用于当前中国高速铁路的发展。因此，提出一个当前条件下高速铁路环境振动标准是十分必要的。

2.4 回归分析

对郑西高铁高架段和路堤段的现场实测值进行统计，采用回归方法拟合出地面振动（VL）的级衰减公式，可以得到高架段和路堤段Z振级随距轨道中心线距离（r）的关系。国内外较多学者对铁路列车引起的环境振动进行了大量的研究，建立了很多地面振动预测模型。

（1）日本川崎公害研究所

（2）日本京都公害研究所

（3）同济大学

可以看出振动级和距离的对数之间基本呈线性关系。

根据现有研究结果，本文建立模型：

利用最小二乘法进行估计，拟合的方程为：

式中：R——相关系数。

将式（8）与式（4）——（6）预测结果进行比较，见图9。Z振级随距离的衰减符合对数衰减规律，除反弹增大区外，拟合效果较好。拟合公式与实测值相比，高架段最大偏差8.15 dB，路基段最大偏差2.42 dB，最大偏差均出现在反弹增大区，可见这种预测方式本身具有的缺陷，即无法表征振动传播过程中的反弹增大行为。式（4）——（6）均是针对高架铁路提出的环境振动公式，相较于日本京都公害研究所提出的式（5），式（4）和式（6）与本文高架段的测试结果较接近。

图9 地面振动预测结果与实测结果的对比Fig.9 Comparison of the ground vibration prediction and measured results

3 无限元-黏弹性耦合边界数值模型

3.1 模型基本设置

为研究空沟及沟内填充材料对减振效果的影响，采用有限元软件ABAQUS进行模拟分析。数值模拟时参考郑西高铁工程的实际情况建模，模型沿轨道方向长度取255 m，与轨道中心线垂直的水平方向长度取250 m，土体厚度取50 m。空沟位置距路堤坡脚20 m，沿线路方向长度为20 m，宽度为1 m，深度为6 m。

无砟轨道结构形式复杂（图10），考虑到本文研究重点是土体振动传播问题，在建模时进行了一定程度的简化处理。钢轨横截面按照截面惯性矩等效的原则简化为矩形横截面（0.1 m×0.2 m），轨距取1.435 m。不考虑轨道板间纵向连接，对其在纵向上进行整体建模，简化为矩形横截面（2.4 m×0.2 m）。砂浆填充层的宽度设置与轨道板等宽，厚度取0.05 m。混凝土支撑层横截面尺寸为3.0 m×0.3 m。不对扣件进行实体建模，用弹簧模拟钢轨和轨道板之间的相互作用，扣件纵向间距取0.65 m。

图10 无砟轨道结构示意图Fig.10 Schematic diagram of the ballastless track structure

路堤断面尺寸参考《高速铁路设计规范》（TB 10621——2014）[23]中无砟轨道单线路堤的标准横断面尺寸（图11）。基床表层厚0.4 m，基床底层厚2.3 m，基床表层顶部宽度8.6 m，基床以下路堤厚3.6 m，路堤边坡取 1∶1.5。

图11 无砟轨道单线路堤标准横断面图（单位：m）Fig.11 Schematic diagram of the standard cross-section of single-line embankment for ballastless track (unit: m)

边界条件为土层底部固定约束，四面侧边界均为接地阻尼弹簧（黏弹性边界），地表面为自由面。为提高计算效率，轨道附近网格划分的较细，逐渐向外过度到较粗的网格。最终建立的轨道-土体数值模型见图12。

图12 轨道-土体数值模型图Fig.12 Diagram showing the track structure-soil numerical model

3.2 材料参数及本构模型

钢轨、轨道板、支撑层均采用线弹性本构模型。路堤及周围土体采用Mohr-Coulomb理想弹塑性本构模型。模型基本材料参数见表3。

表3 基本材料参数Table 3 Basic material parameters

黄土的剪切模量取38.76 MPa，等效波速取250 m/s。考虑到振动波在土体中传播时会不断发生衰减，本文采用瑞利阻尼定义土体阻尼，阻尼系数α取0.616，β取0.000 312[24]。沟内填充材料选用常见工程材料，分别取混凝土、橡胶、石膏、泡沫塑料等材料。填充材料参数见表4。

表4 填充材料参数Table 4 Filling material parameters

3.3 相互作用设置

钢轨与轨道板的接触力学行为，法向为允许分离、不可穿透的硬接触形式。二者之间的扣件采用3个方向的Axial连接器模拟，见图13。纵向方向上每组扣件的纵向阻力取30 kN/组，临界位移为2 mm。垂直方向上扣件刚度取50 kN/mm，阻尼系数取60 （kN·s）/m，扣件垂向力取35 kN，力学行为上为只能受拉不能受压的非线性行为。

图13 扣件预紧力Fig.13 Application of fastener preload

考虑到组成轨道结构的各层间以及轨道结构和地基土之间的滑动相对很小，所以各部分之间采用绑定连接。

3.4 无限元-黏弹性边界条件

在涉及到无穷大介质的动力分析中，若简单地采用人工截断边界，则会导致应力波在边界界面上发生反射，使得本该传向无穷远的能量反射回分析区域，直接影响到分析结果的准确性。ABAQUS无限元理论是通过在边界上引入阻尼力吸收能量。通过手动编辑inp文件修改关键字将模型底部的C3D8R单元改为CIN3D8单元，即外层单元变换成无限元。

黏弹性边界由弹簧和阻尼器组成[25]。

切向边界：

法向边界：

式中：kt——弹簧法向刚度/（Pa·m−1）；

kn——弹簧切向刚度/（Pa·m−1）；

R——波源至人工边界点的距离/m；

G——剪切模量/Pa；

αt——切向黏弹性人工边界参数；

αn——法向黏弹性人工边界参数；

ρ——介质质量密度/ （kg·m−3）；

cs——横波波速/ （m·s−1）；

cp——纵波波速/ （m·s−1）。

刘晶波等[26]建议对于三维问题，αt的取值范围为[0.5, 1.0]，推荐取值为 0.667；αn的取值范围为 [1.0, 2.0]，推荐取值为1.333。本文按推荐的值进行取值计算，模型中的边界设置见图14。

图14 黏弹性和无限元边界Fig.14 Viscoelasticity and infinite element boundaries

3.5 激振力施加

竖向轮轨力主要是由各种不平顺等原因造成的，其主要出现在低频（0.5～10.0 Hz）、中频（30.0～60.0 Hz）和高频（100.0～400.0 Hz）3个范围内。研究表明，竖向轮轨力可以用能够反映其周期特点的激振力表达，文献[27]和[28]均取得了较好的模拟效果。其表达式为：

式中：P0——车轮静载/kN；

P1、P2、P3——对应于表5中Ⅰ、Ⅱ、Ⅲ控制条件下的某一典型振动荷载/kN；

表5 轨道几何不平顺管理值[29]Table 5 Management values under railway geometricregular condition[29]

M0——簧下质量/kg；

ai——对应于表5中Ⅰ、Ⅱ、Ⅲ控制条件下的某一典型矢高/mm；

Li——对应于表5中Ⅰ、Ⅱ、Ⅲ控制条件下的某一典型波长/m；

v——列车运行速度/ （m·s−1）。

英国轨道几何不平顺管理值见表5。

对于高速铁路，本文参数取值分别为：P0=80 kN，M0=750 kg，L1=10 m，a1=3.5 mm，L2=2 m，a2=0.4 mm，L3=0.5 m，a3=0.06 mm。列车时速为240 km时竖向轮轨激振力时程曲线见图15。采用VDLOAD子程序将该激振力以指定的移动速度施加于钢轨上。

图15 时速240 km时竖向轮轨激振力时程曲线Fig.15 Time-history curve of wheel-rail excitation force when v = 240 km/h

4 填充沟隔振效果分析

隔振沟前后#1和#2测点处不同填充材料下的频谱分布见图16。隔振沟可有效的阻隔土体中振动波传播，减弱土体的振动。隔振沟对中高频（30～80 Hz）振动波的隔振效果较低频（1～20 Hz）振动波明显，可见其低通滤波作用。其原因在于低频波长和隔振沟尺寸处于同量级，当低频振动波到达隔振沟时，不发生反射而只进行散射和衍射，使得低频波绕过隔振沟，起不到隔振效果。中高频波到达隔振沟时，会遵循波的反射原理，使其改变传播方向，起到了隔振的效果。不设隔振沟时，地面振动的中高频部分本身也会随着距离增大向线路两侧迅速衰减。因此实际工程中隔振沟不可设置在距线路较远的位置，否则起不到隔振的效果。建议在满足规范要求的条件下，尽可能的靠近线路，且最远不超过30 m。

图16 #1和 #2测点处不同填充材料下的频谱曲线Fig.16 Spectrum curves under different filling materials at measuring points #1 and #2

不同填充材料下Z振级衰减状况见图17。线路设有隔振沟时，隔振沟后土体振动都呈现一定程度的衰减。无填充物的空隔振沟隔振效果最好，但是空沟受到长期列车振动影响后极易发生局部失稳而塌陷。因此在空隔振沟施工过程中要重点对沟壁进行处理。对于填充沟，数值模拟计算结果显示，各隔振材料的隔振效果由优至劣分别为：泡沫塑料>石膏>橡胶>混凝土。因此对于实际工程，可以考虑在空沟中填入泡沫塑料等材料，在保证隔振效果的同时又可以增强沟壁的稳定性。

图17 不同填充材料下Z振级衰减曲线Fig.17 Attenuation of Z vibration level with distance under different filling materials.

5 结论

本文对郑西线高架段和路堤段展开现场测试，对比分析了高架段和路堤段地面振动特征及其衰减规律。建立了路堤段三维轨道-土体-隔振沟数值模型，分析了隔振沟的减隔振作用。主要得出以下结论：

（1）路基段的振动响应大于高架段，高架段近场区衰减作用高于路堤段近场区域。发现振动传播过程中存在2次反弹增大现象，路堤段地面振动反弹增大位置滞后于高架段。高架段和路堤段的二次反弹增大率均明显大于一次反弹增大率。

（2）Z振级随距离的衰减符合对数衰减规律。拟合得到黄土地区高架段和路堤段的Z振级衰减公式，高架段最大偏差8.15 dB，路基段最大偏差2.42 dB，最大偏差均出现在反弹增大区。

（3）使用无限元-黏弹性耦合边界可以得到较好的模拟结果。隔振沟对中高频（30～80 Hz）振动波的隔振效果较低频（1～20 Hz）振动波明显，其具有低通滤波作用。隔振沟不可设置在距线路较远的位置，建议尽可能的靠近线路，且最远不超过30 m。

（4）空沟比填充沟隔振效果好。考虑到沟壁的稳定性，可在空沟中填入软质材料以增强沟壁的稳定性，同时起到隔振效果。

同时，目前我国对高速铁路环境振动的评价均参考20世纪80年代的标准，该标准基于我国当时的铁路状况制订，没有预先考虑高速铁路的情况。因此，亟待提出一个适用于当前条件的高速铁路环境振动标准。