程序设计竞赛中线段树的四类典型应用场景*
符智基,赵义霞,刘 利
(惠州学院计算机科学与工程学院,广东 惠州 516007)
0 引言
高校对学生算法的理解和设计能力的培养越来越重视。许多程序设计类竞赛中也很重视学生的代码把控能力和团队配合能力[1-4],这类竞赛能够检测学生算法水平以及学校算法教学成果。“线段树”作为经典的数据结构,是程序设计竞赛的高频考点。
在程序设计竞赛中,线段树应用场景复杂,灵活多变,不单独作为模板考察。现有教材[1-7]阐述了线段树的基本理论和模板实现,未对其在竞赛中的应用场景进行归类总结。学生尽管学习了线段树的基本用法,但在面对竞赛题目时仍束手无策。
本文针对以上问题,根据现有资料进行深入研究,结合参加ACM 竞赛的经验,归纳出了关于线段树在程序设计竞赛中的四类典型应用场景。以此帮助学习者建立线段树在程序设计竞赛中的应用体系,降低学习难度,提升学习效率。
1 线段树的简介
线段树是一种用于存放与处理给定区间信息的数据结构,形如一棵二叉树,每个节点代表一段连续的区间。可以在单次O(log N)时间复杂度下实现单点修改、单点查询、区间修改、区间查询。
对于表示区间[L,R]的节点,其左儿子代表的区间为[L,M],右儿子代表的区间为[M+1,R],其中M=。每个节点往下延申都二分其区间长度,因此,存储区间大小为N的线段树的深度为,这是线段树一系列操作时间复杂度为O(log N)的重要前提。存放区间信息[1,N]的线段树全部节点个数不超过,编程时,使用大小为4×N的数组存储,空间复杂度为O(N)。
2 四类典型应用场景
在程序设计竞赛中,线段树能与字符串、图论、计算几何、动态规划等算法混合使用,起到降低原算法时间复杂度的作用。例如:维护动态字符串的哈希值、优化扫描线算法、优化建图等等。其用法各式各样,灵活多变。下面通过例题分析的形式,对四类典型应用场景进行描述,每类场景均附相同类型的题目推荐。例题的参考代码可从作者博客(https://blog.csdn.net/m0_68776464?type=blog)获得。题目的来源网站有POJ(http://poj.org/),HDU(http://acm.hdu.edu.cn/),CF(https://codeforces.com/),洛谷(https://www.luogu.com.cn/)。
2.1 扫描线算法的优化
扫描线算法多用于求解二维平面上多个矩形的面积覆盖和周长问题,维护矩形重叠区域的信息。矩形个数为N时,朴素的扫描线算法的时间复杂度为O(N2),使用线段树可以将其时间复杂度优化至O(N log N)。
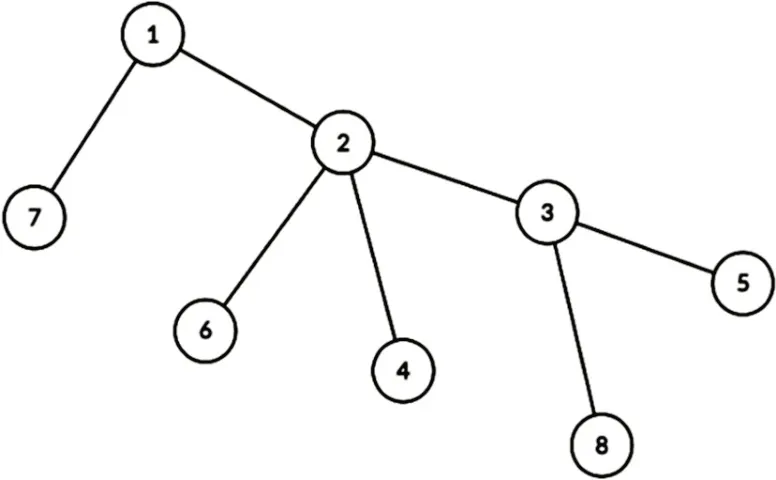
例题(POJ1151):二维平面上N个矩形,每个矩形给出左下角坐标(lx,ly)和右上角坐标(rx,ry),计算被矩形覆盖的区域面积,被多个矩形覆盖的区域只计算一次。其中1 ≤N≤105,1 ≤lx 使用一条平行于X轴的扫描线,从下往上扫描。定义一个整型数组cn t,cn t[i]表示扫描线[i-1,i]处被几个矩形覆盖。扫描线遇到矩形平行于X轴的边时停下计算贡献,再更新cn t数组。扫描线两次停止位置之间的区域,被矩形覆盖的面积为“扫描线移动的距离”与“cn t数组中大于0 的元素个数”的乘积。图1所示例子具体过程如下。 图1 poj1151举例图 ⑴扫描线在y1 开始,cn t数组元素全置0。cn t数组中[x1+1,x3]的值全部要+1。 ⑵扫描线在y2 停下。cn t数组有x3-x1 个大于0 的元素,扫描线移动距离为y2-y1,扫描区域矩形覆盖的面积为(x3-x1)×(y2-y1)。cn t数组中[x2+1,x4]的值全部要+1。 ⑶扫描线在y3 停下。cn t数组有x4-x1 个大于0的元素,扫描线移动距离为y3-y2,扫描区域矩形覆盖的面积为(x4-x1)×(y3-y2)。cn t数组中[x1+1,x3]的值全部要-1。 ⑷扫描线在y4 结束。cn t数组有(x4-x2)个大于0的元素,扫描线移动距离为y4-y3,扫描区域矩形覆盖的面积为(x4-x2)×(y4-y3)。cn t数组中[x2+1,x4]的值全部要-1。 被矩形覆盖的区域总面积等于过程①~④所求面积的总和。将每个矩形区域(lx,ly,rx,ry)拆分成两个事件:(ly,lx,rx,1)和(ry,lx,rx,-1)。将全部事件按照y值排序,每个事件对cn t数组的更新区域为[lx+1,rx],是一段连续的区间,均为区间加减。因此可以使用线段树优化,维护cn t数组中大于0 的元素的个数,时间复杂度为O(N log N)。需要注意的是,该题矩形坐标范围较大,需要将坐标值离散化处理。 同场景题目——洛谷P1502、POJ1177、POJ2482、HDU1255、HDU3255、HDU3265。 许多关于树形结构的题型,涉及子树或树上路径信息的修改与查询。类似于这种树上问题,如果每次操作都逐点遍历,单次操作的时间复杂度为O(N)。先利用dfs 序、树链剖分等方法将树结构区间化,再用线段树维护,可将单次操作时间复杂度降低至O(log N)。 例题:一棵具有N个节点的有根树。Q次操作,操作有两种:①修改树上某个节点的权值;②查询树上某棵子树全部节点的权值和。 如图2 所示,一棵以节点1 为根的树。对该树dfs遍历,得到一种可能的入栈顺序为[1,7,2,6,4,3,8,5]。可以发现,以任意节点为根的子树,子树内全部节点都在dfs序列的其中一段连续区间(该子树根节点入栈和出栈的时间区间)。利用这个性质操作:①转换为线段树在dfs 序列的单点修改,②转换为线段树在dfs 序列的区间查询。 图2 树形结构举例图 同场景题目——洛谷P3384、POJ2763、POJ3237、HDU3966、CF343D、CF877E。 线段树常用于维护带修改的结合律信息,最经典的有加减法、乘法、动态字符串的哈希值等等。这类信息在修改了某个下标的元素后,包含该下标的全部子区间都会受到影响。每次询问区间最优解的时间复杂度为O(N)。可以利用“线段树节点中,包含某个下标的区间节点个数最多为个”这一性质,自下往上利用线段树合并更新,快速算出全局最优解,单次询问时间复杂度降低为O(log N)。 例题(CF1609E):一个长度为N且仅由字符'a','b','c'组成的字符串S。Q次操作,每次操作给出一个整数pos和一个字符ch,表示将字符串中下标(从1 开始)为pos的元素替换为ch。每次操作后,输出至少需要修改几个位置的字符,才使得字符串不包含子序列"abc"。其中1 ≤N,Q≤105,1 ≤pos≤N,ch∈['a','b','c']。 每次修改后遍历字符串判断是否包含子序列"abc",时间复杂度为O(N×Q)。 选取任意满足范围要求的k,得出结果一致,答案为min{Cost[1][N][0][t]},(0 ≤t≤2)。 线段树的节点[L,R]维护一个4×4 的二维数组,表示Cost[L][R][][]。修改下标pos,仅需修改线段树中包含pos的节点,每个节点利用左右儿子合并更新,总时间复杂度为O(43×Q×log N)。同场景题目——HDU4578、HDU3973、HDU3308、CF-gym102798G。 使用线段树对动态规划的转移过程进行优化,在程序设计竞赛中屡见不鲜。荆慧[8]、邹玉金[9]也提出了基于线段树的动态规划优化算法,对“最长上升子序列”、“邮局问题”两类经典动态规划问题进行了优化。除这两类问题外,仍存在许多动态规划问题可以使用线段树进行优化,这些问题都具有一个共同点——“其转移过程中的子问题满足区间连续”。 例题(原创):长度为N的整形数组A(下标从1 开始),递增度为。选择一段任意长度的区间[L,R]反转。例如数组A=[1,2,3,4,5,6],反转区间[2,5],数组变成A=[1,5,4,3,2,6]。一次区间反转后数组的递增度最大为多少?其中1 ≤N,Ai≤105。 一个朴素的做法,枚举全部可能操作的区间,对于每种操作都遍历一遍数组计算递增度,时间复杂度为O(N3)。 优化遍历计算递增度这一过程,定义两个整型数组sum和rev。其中sum[i]表示子数组[1,i]的递增度,rev[i]表示子数组[i,N]反转后的递增度。枚举反转区间[L,R],反转后的数组的递增度可以O(1)计算,时间复杂度为O(N2)。公式如下: 枚举反转区间[L,R]的右端点R,令X=sum[N]-sum[R+1]-rev[R],对于左端点L,令Y=sum[L-1]+rev[L]。有以下几种情况。 ①1≤AL-1 ②1 ≤AL-1 ③AL-1≥AR,1 ≤AL ④AL-1≥AR,AL≥AR+1。答案为X+Y。 X为定值,Y越大越好。每种情况有两种限制,可以视作在二维平面中,给出左下角和右上角坐标的矩形区域内的最大Y值。每次遍历到下标R,用sum[R-1]+rev[R]来更新坐标(AR-1,AR),维护最大值。二维平面上矩形区域的最值查询,单点修改,可以使用线段树套线段树进行求解。空间复杂度为O(N×log2N),时间复杂度为O(4×N×log2N)。 同场景题目——HDU3016、HDU3607、HDU6447、POJ1769、POJ3171、CF833B。 为了降低线段树的学习难度,本文通过例题,分析、总结并阐述了“扫描线算法的优化”、“树形结构信息的维护”、“带修改的结合律信息的维护”和“动态规划算法的优化”四类线段树的典型应用场景。随着信息技术的发展,近年来提出关于线段树在程序设计竞赛中的新用法,如区间最值操作与历史最值问题、李超线段树等。由于篇幅有限,本文未对其进行讨论。这类线段树的新用法难度较高,本文线段树在程序设计竞赛中的典型应用,可以为学习者建立系统性的认识,为更高难度的应用研究奠定基础。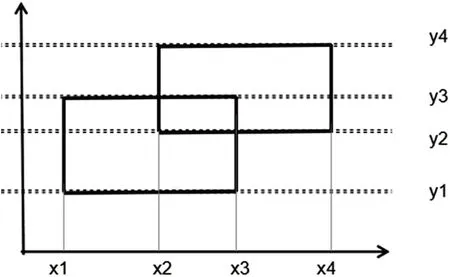
2.2 树形结构信息的维护
2.3 带修改的结合律信息的维护
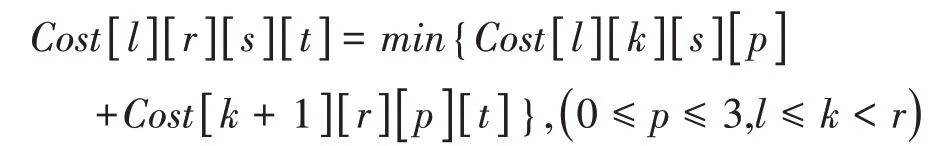
2.4 动态规划算法的优化
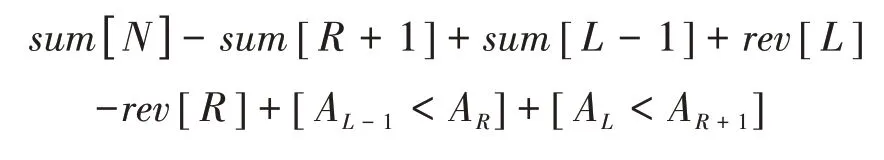
3 结束语

