基于WT-BiLSTM-ARMA模型的PM2.5浓度预测研究＊

程妍菲，张明辉，王宝珠

(河北工业大学电子信息工程学院，天津 300401)

0 引言

近年来，随着工业化进程的不断加快，我国的能源消耗量也在持续增加，导致PM2.5(测量直径为2.5微米或更小的颗粒物)等空气污染物大量聚积[1]。研究表明，长期暴露在含有高浓度污染物的环境中，会给人类的身体健康带来极大危害。不仅如此，空气污染问题也给我国的交通运输、社会经济等带来了重大损失[2]。高效且精准的预报不仅能够为环保部门及时了解未来的空气质量变化趋势提供一定的参考，而且对生态环境的管理和保护有重大意义[3]。

目前已知的预测方法可分为两类：通过机理模型预测和通过统计模型预测。机理模型的本质是根据对大气污染物的产生、转换、扩散的物理化学过程来建模，从而进行后续预测分析[4]。比较典型的有美国的WRF-Chem 模型[5]、CMAQ 模型[6]等，但考虑到预测过程较为复杂、建模难度较大、预测精度不足且难以提升等问题，机理模型并没有得到广泛应用。相较于机理模型，统计模型不用考虑复杂的物理化学过程，建模过程较为简单且预测精度易于优化，因而被广泛使用[7-9]。随着人工智能技术的逐步推广，越来越多的研究人员也致力于将机器学习与该领域相结合的研究，采用基于统计模型的机器学习模型进行空气质量的预测[10-12]。例如，白鹤鸣等人在北京市空气质量数据的基础上建立了BP神经网络模型，得到了较好的预测效果[13]。L 等人将HW(霍尔特-温特斯)与ANN 进行结合应用于里约热内卢的空气质量预测，得到了足够准确的预测结果[14]。Wang 等人采用了Convnet 和基于Densebase 的双向选通循环单元，结合了Convnet、Dense 和Bi-GRU，也获得了较好的预测效果[15]。

随着机器学习研究的不断深入，人工神经网络也在不断丰富和发展[16]。1997 年，Honchreater 和Schmidhuber 两人共同提出长短期记忆神经网络(Long Short Term Memory，LSTM)并于2001年提出了进一步的改进[17]。由于LSTM 神经网络自带循环记忆单元，所以在具有前后依赖关系的时间序列的处理问题上具有自身独特的优势并且能够处理具有较长时滞的序列，广泛应用于各个领域的预测问题上[18,19]。

本文在LSTM 神经网络的基础上，建立了基于双向长短期记忆神经网络(Bi-directional Long Short Term Memory,BiLSTM)的预测模型，相较于传统的LSTM模型，BiLSTM模型的预测效果更为准确。

1 理论支持

1.1 小波分解

小波变换最早由Mallat 提出，Mallat 在Burt 和Adelson的塔形图像分解和重构算法的启发下，提出了小波变换的Mallat 快速算法[20,21]。本文采用小波分解技术对原始的PM2.5 时间序列数据进行处理，将具有高频细节特征的高频信号分离出来，从而获得了更多的数据特征[22]。分解过程表达如下：

其中，H代表低通滤波器，G代表高通滤波器，Aj代表由低通滤波器得到的低频分量，Dj代表由高通滤波器得到的高频分量。而小波变换过程中的分解信号的每一层都是预分解信号的一半，因此我们需要进行两次插值重建来恢复信号长度，重建公式表示如下：

其中，H2和H相对应，G2和G相对应。

本文采用小波分解算法进行四层分解和重构，以获得D1，D2，D3，D4四个高频细节分量和A一个低频近似分量[23]。

1.2 CEEMDAN

自适应噪声完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN) 在经验模式分解(Empirical Mode Decomposition,EMD)的基础上，叠加了集成经验模式分解(Ensemble Empirical Mode Decomposition,EEMD)中的加入高斯噪声和通过多次叠加并平均来抵消噪声的思想。信号分解能力更强，更有利于特征的提取[24]。

1.3 BiLSTM

本文在LSTM 的基础上对高频分量进行预测[25]。LSTM 是长短期神经网络，与RNN 模型的功能相类似，用于表示时间序列数据的动态时间行为。不同的是，LSTM 中的隐藏层被一个长短期记忆单元所取代。因此，相较于传统的RNN 模型，LSTM 模型可以解决长期依赖性和消失梯度的问题。然而，LSTM 的隐藏层只能获取过去的特征。因此本文采用BiLSTM 模型，从而可以更好地理解过去和未来两个方向的时间序列数据，进行更加准确的预测。BiLSTM 层结构如图1所示。

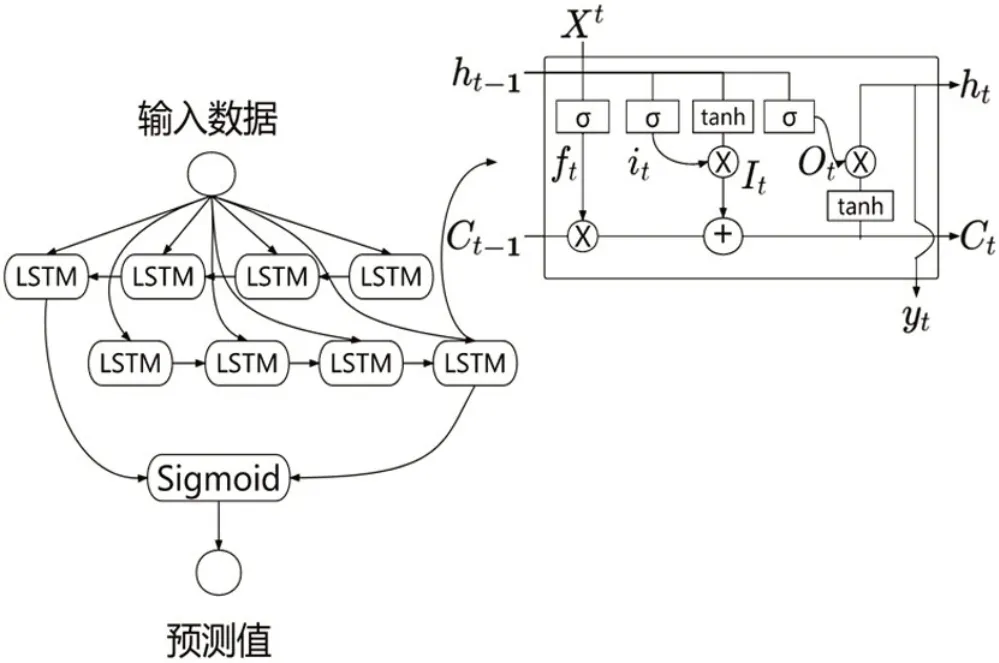
图1 BiLSTM结构

图1 中，一个LSTM 单元由一个输入门、一个输出门和一个忘记门组成，且LSTM 有两个重要属性，一个是随着时间而变化的隐藏层ht,另一个是维持长期记忆的细胞Ct。Ct由此时的输入门it、遗忘门ft和前一时刻的隐藏层ht-1和记忆细胞Ct-1决定，而隐藏层ht则由记忆细胞Ct和此时的输入数据确定，表示为：

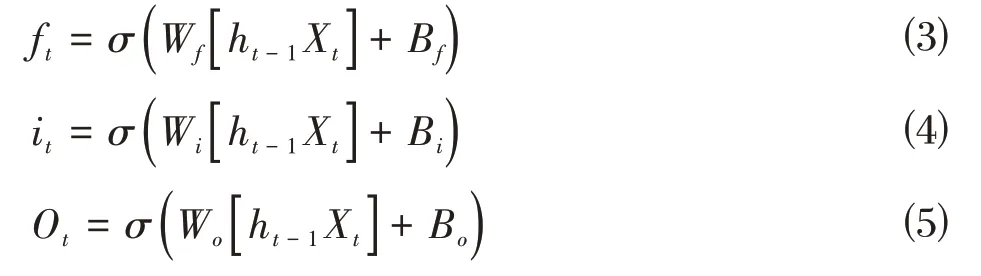
其中，W和B分别表示通过模型训练获得的权重矩阵和偏差向量。σ表示sigmoid 激活函数，“·”表示元素对元素的乘积。

1.4 ARMA

自回归滑动平均模型(Autoregressive Moving Average Model,ARMA)由自回归模型(Autoregressive Model,AR)与移动平均模型(Moving Average Model,MA)混合得到。它通过对扰动项进行模型分析来将过去值、当前值和误差结合起来，是研究平稳时间序列的一种重要方法[26]。本文采用ARMA 模型对小波分解所得的低频近似分量进行预测。数学模型如下：

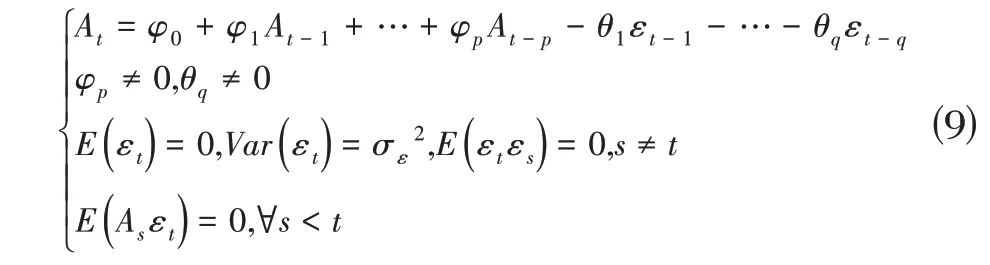
其中，A表示输入数据，φ表示自回归模型系数，φ0是一个定值，θ表示滑动平均模型系数，εt表示白噪声过程。p和q表示ARMA 模型的两个系数，其中pp 表示延迟算子，q表示滑动平均窗口的大小。

2 模型建立

2.1 数据来源

本文研究数据来源于北京市生态环境监测中心，包括2017 年1 月-2020 年1 月北京市6 个国控站点测得的PM2.5浓度数据，如表1所示。

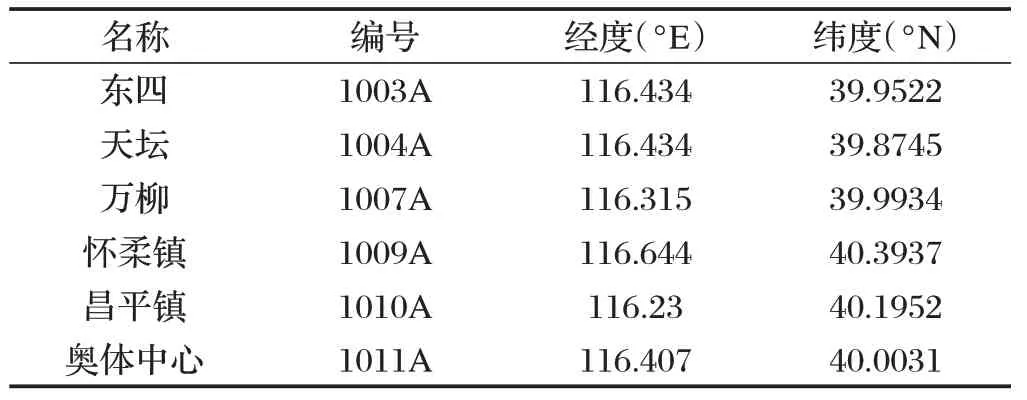
表1 北京市六个大气污染国控站点坐标

2.2 WT-BiLSTM-ARMA模型

WT-BiLSTM-ARMA 模型预测流程如图4 所示。以下具体描述建模步骤，其中步骤四和步骤五为模型创新点。

图4 预测流程

步骤一对原始数据进行归一化处理：

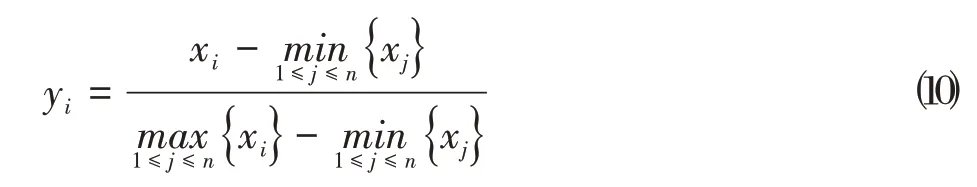
其中，xi表示原始序列，n表示序列长度，yi表示归一化结果。

步骤二对数据进行四阶小波分解，得到四个高频信号D1，D2，D3，D4和一个低频信号A。将分解结果按3:1 的比例分为训练集和测试集。此处以天坛监测站的PM2.5 数据集为例，得到结果如图2 和图3 所示。其中图2为分解得到的低频序列，可以看出低频序列A具有明显的趋势性和一定的周期性。而图3中的高频序列D1-D4则明显反映了原始时间序列趋势的随机波动变化。

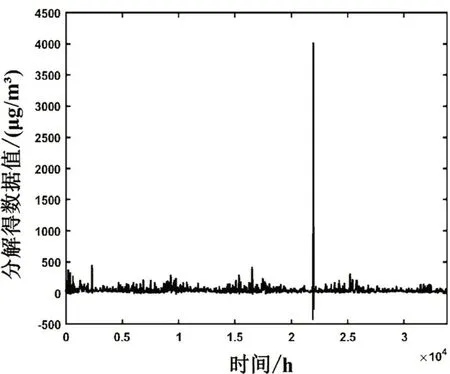
图2 小波分解得低频序列

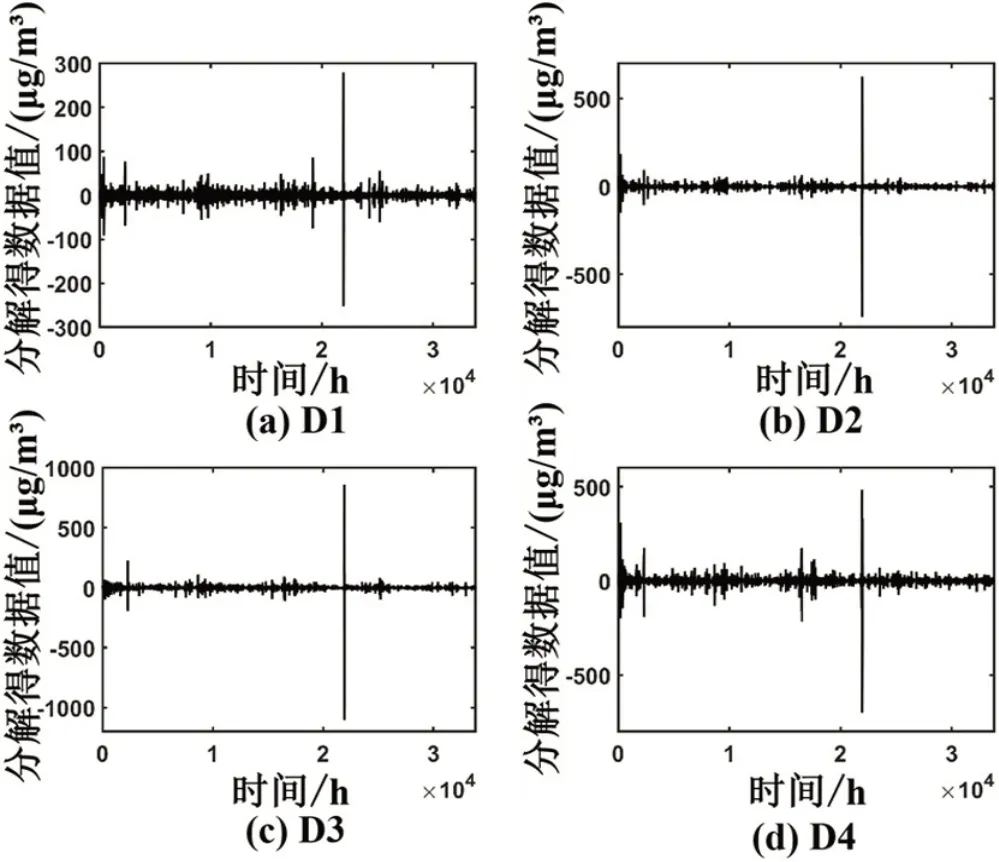
图3 小波分解得高频序列

步骤三将小波分解得到的四个高频信号进行数据处理，从而获得BiLSTM 模型和ARMA 模型对应的输入特征。

步骤四将步骤三的结果输入BiLSTM 模型进行训练并将小波分解得到的低频信号A 输入ARMA 模型进行训练。

步骤五将测试集数据输入训练后的BiLSTM 和ARMA 模型，获得各自的预测结果，并通过对各个预测结果进行小波重构得到最终预测值。

2.3 预测效果评价指标

本文采用平均绝对误差MAE、均方根误差RMSE和方差R2作为指标来对预测结果进行评价。

MAE 表示所有单个预测值与算术平均值的偏差的绝对值的平均，反映了预测值误差的真实情况，模型越完美，该值越小。

RMSE 又称标准误差，是预测值与真实值偏差的平方值与观测次数n比值的平方。模型的精度越高，该值越小。

R2为拟合优度的统计度量，其值越接近1，表示模型拟合越好。

三项指标表示如下：

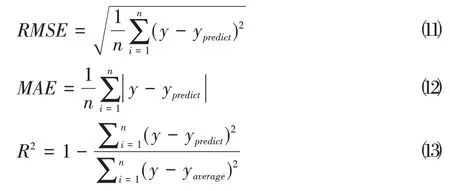
其中，y为数据实际值，ypredict为模型得到的预测值，n表示数据集的长度。

2.4 预测结果

预测结果如表2和图5～图10所示。

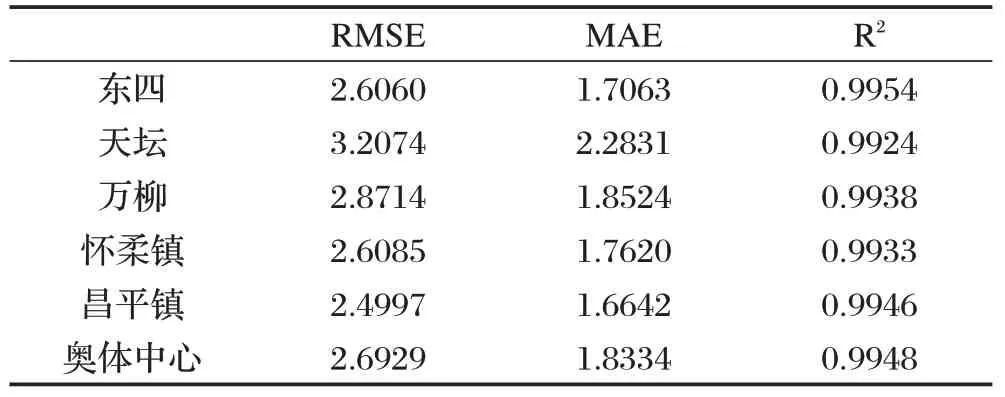
表2 各监测点预测结果

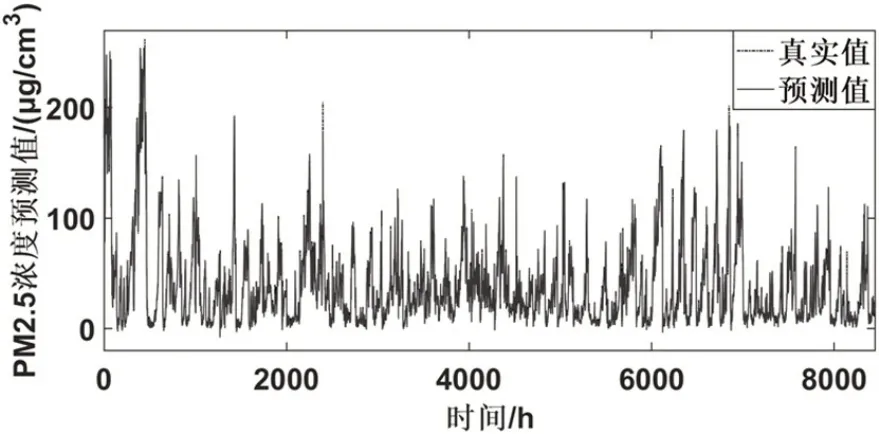
图5 东四监测站预测结果

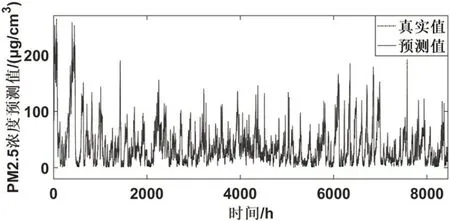
图6 天坛监测站预测结果

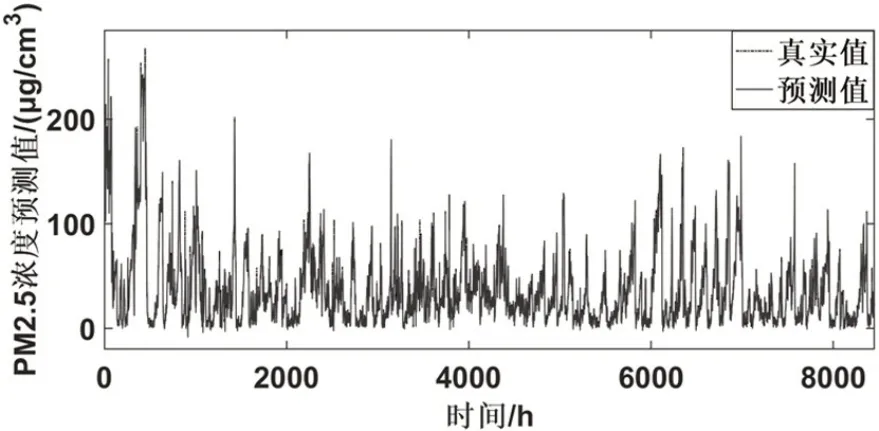
图7 万柳监测站预测结果

图8 怀柔监测站预测结果

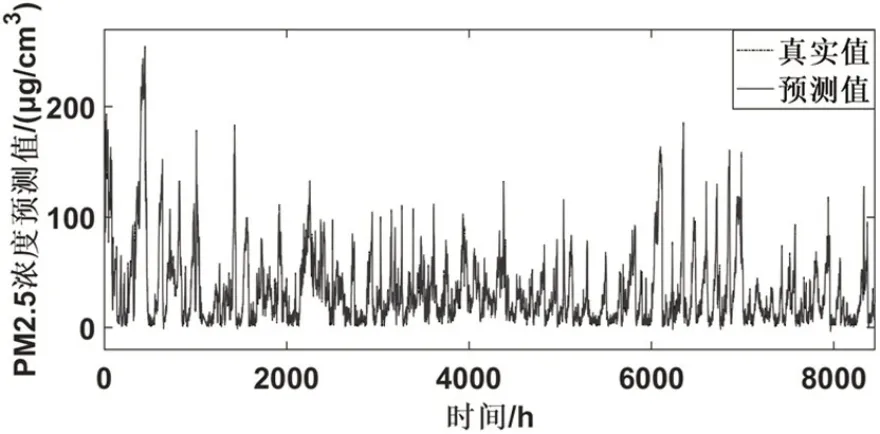
图9 昌平监测站预测结果

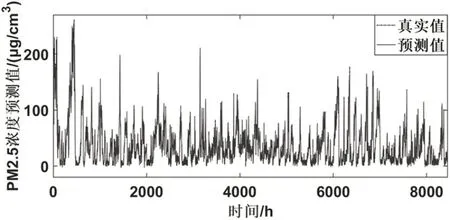
图10 奥体中心监测站预测结果

表2 记录了WT-BiLSTM-ARMA 模型在六个监测点的PM2.5 浓度数据的基础上得到的预测结果。图5-图10 为WT-BiLSTM-ARMA 模型在六个监测点的数据的测试集的基础上得到的预测值与真实值的对比结果。

3 对比分析

3.1 模型对比

为了验证本文提出的预测模型的精确度和有效性，本文将所提出模型与其余几种预测模型进行了对比分析，包括单一模型LSTM、BiLSTM、ARMA 以及混合模型WT-BiLSTM 模型和CEEMDAN-BiLSTM模型[27]。如图11 所示，WT-BiLSTM 模型将小波分解得到的所有序列送入BiLSTM 模型进行预测，而CEEMDAN-BiLSTM 模型是采用CEEMDAN 分解方法对原始数据进行分解。

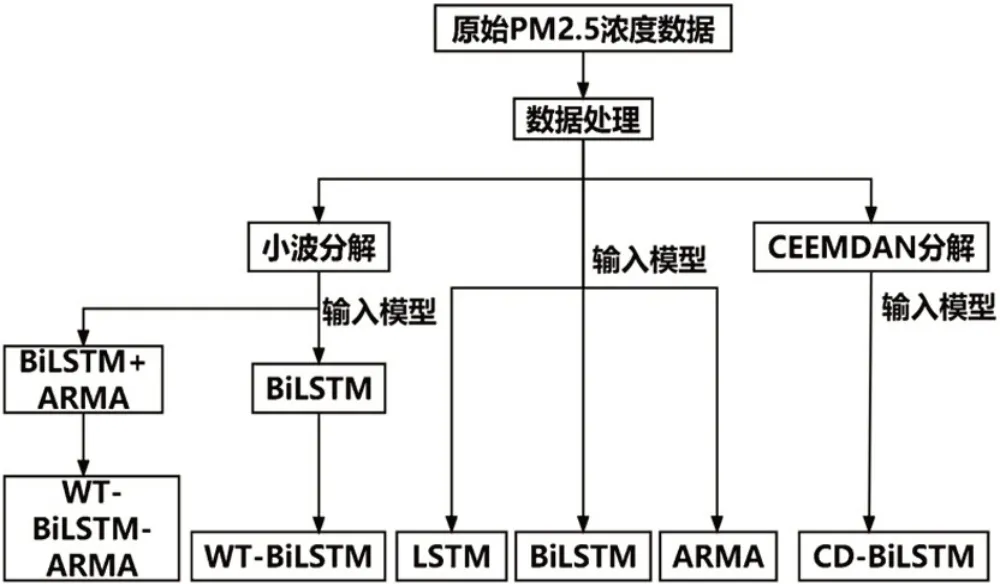
图11 模型对比

3.2 结果对比

本文将六个监测点的数据输入各个模型并求得结果的平均值，比对结果如表3所示。

由表3 可得，单一预测模型ARMA、LSTM 和BiLSTM 均取得了较好的预测效果，但多次试验所得数据证明BiLSTM 的预测效果要好于LSTM 和ARMA。但由于PM2.5 数据本身存在自相关性，所以单一模型的预测结果存在一定的滞后问题。

与单一模型相比，CEEMDAN-BiLSTM 模型的预测精度有所提高，但是存在总体预测值小于实际值的问题，且模型运行时间过长。因此，WT-BiLSTM 模型和WT-BiLSTM-ARMA 模型的预测结果更为精确且实用性更强。由于ARMA 更适用于低频数据的预测，所以我们将低频分量A输入ARMA 模型时所得到的结果更为精确。

通过对预测结果评价指标的全面分析，本文提出的WT-BiLSTM-ARMA 模型与单一模型BiLSTM 相比，RMSE 降低了66.8%，MAE 降低了64%，R2提高了5.03%；与混合模型WT-BiLSTM 相比，RMSE 降低了40.5%，MAE 降低了50.2%，R2提高了1.15%，具有更高的预测精度。

4 结束语

随着全球范围内空气质量的不断恶化，精准的空气质量预测对生态治理和环境保护工作都具有重大意义。本文提出的WT-BiLSTM-ARMA 模型可以通过小波分解算法在大量原始数据中提取出周期特征和随机特征，得到了较高的预测精度，具有良好的推广性。本文将所述模型与单一模型LSTM、BiLSTM、ARMA 以及混合模型CEEMDAN-BiLSTM 和WTBiLSTM 进行了对比。实验结果表明，该模型更适合于PM2.5的预测。

本文的研究不足之处在于仅以时间的维度作为自变量进行分析，忽略了空间维度的影响。未来可以结合其他时间序列分析模型、空间分析模型以及数据分解方法进行改进，以获得更好的预测结果。本模型也可按需应用于燃气负荷，短期网络流量以及短期人流量等预测问题。