基于率相关土水特征曲线的边坡稳定性分析

于建涛

（中铁第五勘察设计院集团有限公司，北京 102600）

降雨入渗诱发的边坡失稳现象是一个典型的非饱和土问题。国内外学者对边坡稳定问题进行了非常深入的研究，提出了很多边坡稳定性安全系数的计算方法，其中最常用的方法有极限平衡法和强度折减法。采用这些方法去分析非饱和土边坡稳定时，含水量对土体力学行为的影响研究是其中的一个关键问题。降雨入渗使得边坡非饱和土体的基质吸力降低，进而导致非饱和土的强度降低，降低了边坡稳定性，诱发滑坡。常规的土坡稳定性分析方法主要是基于饱和土理论和稳定渗流情况，难以反映降雨作用和水位骤降对边坡稳定的影响，而相当一部分坡体失稳是由于非饱和非稳定渗流引起的[1]。因此有必要采用瞬态或者非稳定渗流模型，对边坡稳定进行分析预测[2-3]。

在各种边坡稳定分析方法中，土水特征曲线（Soil-Water Characteristic Curves，简 称SWCC）是必不可少的，它描述了土含水量与基质吸力之间的关系，有助于分析土体的力学行为。目前SWCC模型发展较为完善，从早期的经验模型，到可以反映滞后行为的各种理论模型，以及可以考虑土体变形、温度等复杂因素影响的模型。但是这些模型大部分是在平衡条件下得到的，现有的研究已经证实，瞬态条件下测得的SWCC与静态或平衡态测得的SWCC并不重合，SWCC存在明显的动态效应[4]。Hassanizadeh等[5]的试验结果显示，干燥过程中，动态吸力比静态结果高，而湿化过程中，动态吸力比静态结果低。

尽管非饱和土瞬态渗流模型也可以反映非饱和土中液体流动和含水量随时间的变化，但其中所采用SWCC仍是在平衡条件下得到的。Diamantopoulos等[6]发现基于平衡态SWCC的Richard方程无法准确预测分步排水实验中的水头变化。此外，这种率效应对水力参数也会产生影响[7]，采用平衡条件下得到的水力参数预测瞬态渗流问题也会使预测结果出现误差。因此有必要考虑SWCC的率效应对于边坡稳定的影响，建立基于率相关SWCC的边坡稳定分析模型。

1 率相关SWCC

1.1 率相关SWCC的理论基础

刘艳等[8]从热力学基本平衡方程出发，考虑土体内部的交界面影响，给出了非饱和土流体的熵增不等式

式（1）中第一项是孔隙流体的压力差，第二项代表宏观毛细力。Hassanizadeh等[9]指出毛细力本质上是气液交界面上的一种作用力，并不等同于界面两侧流体的压力差，并可将宏观毛细力表示为

在线性假设条件下，根据熵不等式（1）可以得到液相广义力与广义流之间本构关系如下

1.2 非饱和土渗流的基本方程

非饱和土的渗流一般可以采用Richards方程来进行描述，即

式中：h为总水头，C（h）为比水容量，kx、ky、kz为各方向的渗透系数，通常可以表示为含水量或吸力的函数，可按式（5）计算

式中：ks为饱和渗透系数。

显然求解式（4）需借助于SWCC，这里选用VanGenuchen模型，其一般形式可以表示为

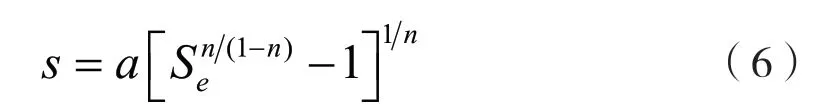
式中：n、a为经验参数；Se为有效饱和度。

在瞬态入渗的过程中，SWCC具有率效应。将式（6）代入式（3）中可得到率相关的SWCC方程，

利用式（7），可以计算出考虑率效应后的比水容量C（h）。同时将式（7）代入式（5）中，得到考虑率效应后的渗透系数计算式，即

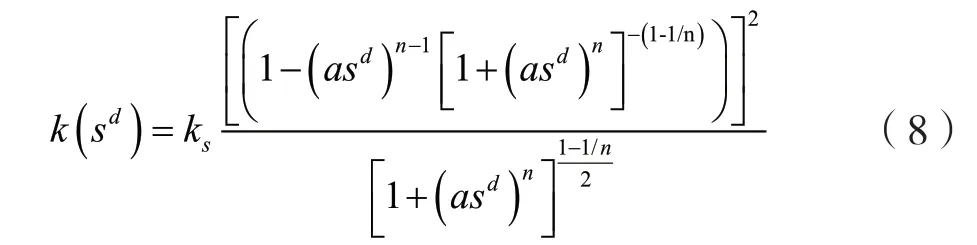
可以看出，率效应不仅影响SWCC，也将改变水力参数，在分析土坡稳定时，有必要考虑这种影响。

2 瞬态入渗边坡安全系数

2.1 抗剪强度准则

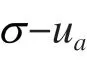
如果考虑SWCC的率效应对安全系数的影响，需将式（7）代入式（9）中，可以得到即得到考虑率效应的土体强度准则，以下基于该强度准则，计算边坡的安全系数。

2.2 安全系数计算模型

目前已有很多计算边坡安全系数的方法，比 如 瑞 典 法、Bishop法、Janbu法、Spencer法、Morgenstern-Price法、Sarma法等。本研究采用基于率相关的SWCC来计算安全系数，并与现有方法计算结果进行比较，这里选用Bishop条分法。非饱和土边坡受力分析见图1。

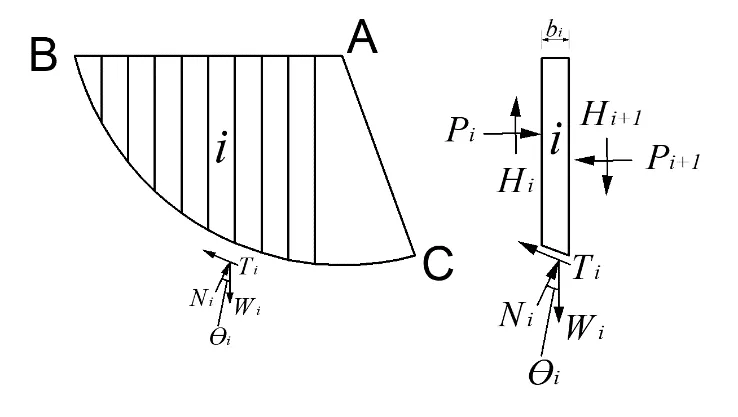
图1 简化Bishop法计算受力图

安全系数等于滑动面上的抗滑力除以下滑力，假设气压保持为大气不变，利用式（10）可以得到下滑力为

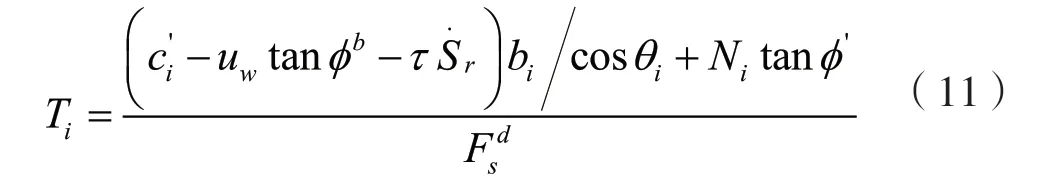
由静力平衡条件∑Fy=0，ΔH=Hi+1-Hi得

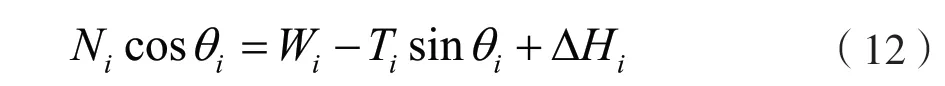
利用式（11）和式（12），消去Ni可得式中

再由静力平衡条件∑Fy=0，ΔPi=Pi+1-Pi得

对于整个滑动体来说ΔPi=0，且将式（12）带入式（15）可以得到

将式（16）带入式（13）可以得到率效应影响的非饱和土边坡的安全系数为

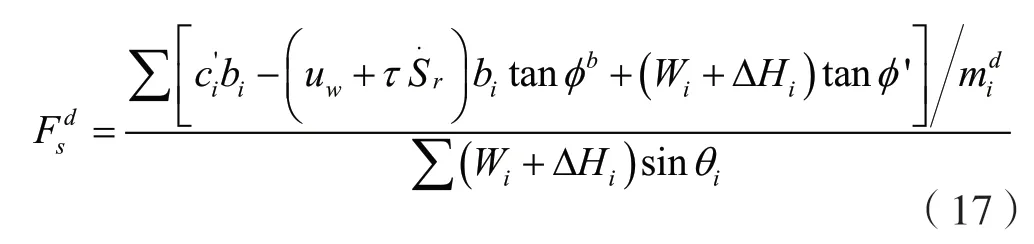
3 计算案例

3.1 计算模型及参数

为分析率相关SWCC对计算边坡稳定性安全系数的影响，选取典型的边坡进行计算，边坡模型如图2所示。坡高为10 m，坡度为37°。边坡左侧水位高为14 m，右侧水位高3 m，左右两侧水位以上为零流量边界。

图2 计算模型

Kitamura等[11]为了探讨非饱和土边坡在降雨外力作用下的边坡机制，用Shirasu土（日本一种典型土）作为试料，进行了大量的不同类型边坡模型试验研究。本研究选取Shirasu土进行边坡数值分析。土体材料参数见表1。

表1 Shirasu土的材料参数

3.2 边界条件及SWCC

降雨边界见图2，选取3组降雨强度（44 mm/d、110 mm/d和220 mm/d）分别计算降雨持续100 h的边坡稳定性。根据Milatz等[12]，将3种降雨强度转换为饱和度变化率（单位均为s-1）数值分别为7.29×10-5、1.82×10-4和3.65×10-4。式（7）中值范围为30～50 000 kPa·s[6]，由于缺少试验数据，假设一个中间值10 000 kPa·s来计算率相关SWCC。

利用式（6）和式（7）可对实验数据[11]进行拟合，所得的SWCC如图3所示，计算得到的是渗透系数与吸力关系见图4。可以看出，如果不考虑SWCC率效应，其SWCC和渗透系数曲线都与降雨强度无关，即图中的率无关曲线。但实际上率效应的存在会明显改变土体的水力参数，不同降雨强度时，SWCC及渗透系数都发生了变化，这种变化必将影响土体力学特性。

图3 Shirasu土的SWCC

图4 Shirasu土渗透系数与吸力的关系

3.3 计算步骤

利用Geo-studio软件进行降雨入渗条件下的边坡安全分析需要用到SEEP/W和SLOPE/W两个模块。

（1）首先利用SEEP/W进行稳态渗流计算，采用图3和图4所示的四种土体SWCC曲线和渗透系数曲线。初始边界为左右两侧的水位和水位上部的不透水边界。对边坡左侧、右侧分别施加14 m、3 m的水头，并在水位上部施加不透水边界，进行稳态渗流计算。

（2）确定计算工况。根据是否考虑率相关及降雨强度，共得到6种工况。

表2 工况表

（3）利用SLOPE/W中的极限平衡法进行边坡稳定性分析，计算各工况边坡安全系数。

3.4 计算结果

3.4.1 孔隙水压力结果

提取不同深度的节点数据进行绘图分析，节点位置见图2，从坡面往下为A～N。图5给出了三种降雨强度下，不同深度的孔隙水压力变化情况，可知，降雨持续时间越长，土体内的孔隙水压力变化越大；44 mm/d降雨强度下，8 h和24 h时率相关和率无关孔隙水压力无明显差别，但随着降雨持续时间的增加，48 h时，率相关和率无关孔隙水压力有了较小差别，100 h时，率相关的孔隙水压力变化明显大于率无关的孔隙水压力变化；而在110 mm/d降雨强度下，降雨持续时间为24 h时率相关和率无关孔隙水压力即有了较小差别，48 h时有明显差别；220 mm/d降雨强度下，降雨持续时间为8 h时率相关和率无关孔隙水压力即有较小差别，24 h时就有明显差别。说明率相关条件下计算所得孔隙水压力变化比率无关条件下计算孔隙水压力变化快，而降雨强度越大，其变化越快，且其差别也越明显。

图5 不同降雨强度下孔隙水压力随深度的变化

3.4.2 安全系数对比

图6给出了不同降雨持续时间下安全系数变化。初始时刻，各工况的安全系数相同。三种降雨强度下，率相关和率无关条件下安全系数均随降雨持续时间的增加降低，当降雨持续一定时间后，边坡安全系数将趋于稳定，降雨强度越大，稳定需要的时间越短。三种降雨强度下，率相关条件下计算的安全系数小于率无关条件下计算的安全系数，降雨前期差别较小，随着降雨持续时间的增加，安全系数差别越来越大。因此，当计算非饱和土边坡安全系数时，应考虑率效应带来的影响。

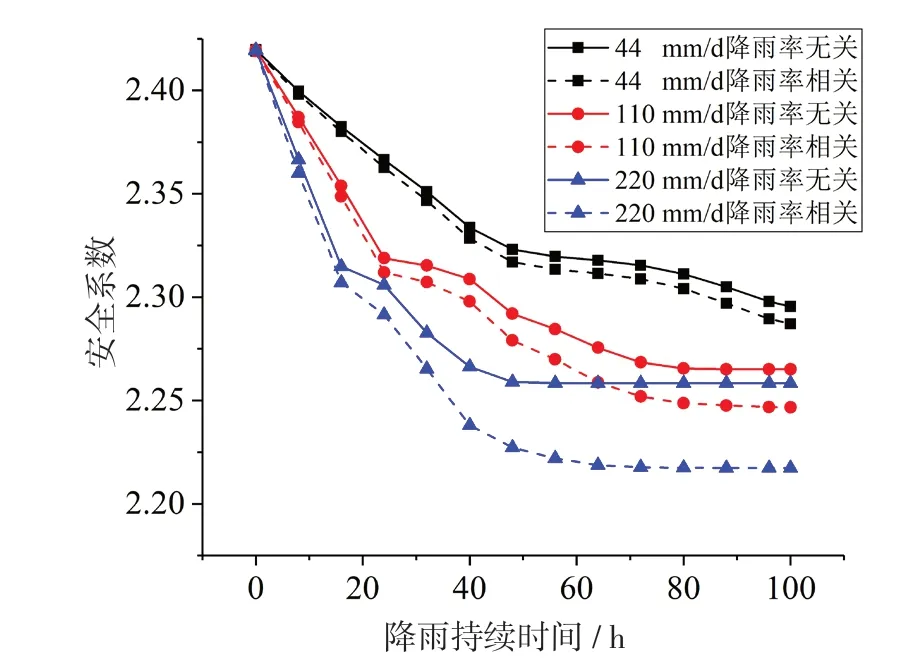
图6 不同降雨强度下安全系数变化图

4 结论

首先介绍了率相关SWCC模型，给出了率效应影响的非饱和土渗流模型并将其引入抗剪强度准则，推导得到了基于率相关SWCC的边坡安全系数公式。采用Geo-Studio软件计算了不同工况下的边坡安全系数。主要结论如下：

（1）在各种工况下计算得到的安全系数，均随着降雨强度的增大而降低。当降雨持续一定时间后，边坡安全系数将趋于稳定。三种降雨强度下，率相关条件下计算的安全系数均小于率无关条件下的安全系数，随着降雨持续时间的增加，其安全系数差别越来越大。说明利用率相关SWCC计算的安全系数和利用率无关计算的安全系数有很大差异，实际应用中需根据降雨强度和降雨持续时间进行具体计算分析。

（2）虽然两种情况下计算所得的安全系数都是随着降雨强度的增大而降低，但是利用率相关SWCC计算的结果变化幅度更大。利用率相关SWCC计算的安全系数更易受到降雨强度的影响。