机载光电随动伺服系统稳速性能与动态特性优化

任元斌,王惠林,杜言鲁,巩全成,王新伟,刘 栋,闫 明

(西安应用光学研究所,陕西 西安 710065)

1 引 言

机载光电平台是集可见光电视、红外热像仪、激光测距机等传感器于一体的航空成像设备。它通常安装在载机下方,在载机飞行过程中,执行瞄准、搜索、监视等任务,为用户提供昼夜高分辨力图像。

从产品功能的角度描述,传统机载光电平台以凝视观瞄为主。近年来,随着航空平台、电子信息、光学设计等技术的发展,用户对机载光电平台逐渐提出了一些新的功能需求,其中包括广域监视。单一视场的小范围成像不足以实现广域监视,扫描成像可对目标区域进行较大范围的视觉态势感知,因此它是实现广域监视的一种较好的途径。

机载光电平台要实现整机扫描成像,需使用万向架往复稳速摆扫,同时使用反射镜[1]反扫来补偿摆扫像移。以往对机载光电平台领域的研究,主要集中在其稳定性能、扰动抑制[2-3]、以及目标快速跟踪[4]上,对于整机扫描成像型随动伺服系统的稳速性能的研究不多。两轴三框架、四框架这类扫描成像型随动伺服系统是通过其内、外万向架[5]随动的方式来实现万向架扫描的,其扫描稳速性能直接决定成像的像质,故对其扫描稳速性能的研究很有意义。

以某型两轴三框架机载光电平台为研究对象,该平台在横滚方向整机扫描成像,其内、外横滚万向架采取内外随动的方式。通过对该系统的扫描原理分析和仿真模型搭建,来定位稳速性能关键影响因素,提升其稳速性能,是一种低成本高效率的分析办法[6-7]。

本文主旨不在于给出一定外部扰动因素,求得系统的稳定精度,而在于通过仿真研究随动伺服系统的稳速机理,寻找和归纳出系统扫描时内部的稳速性能关键影响因素,给出稳速性能的提升方案并进行验证,故未考虑随动伺服系统外部的扰动因素。

2 机载光电随动伺服系统建模

2.1 随动伺服系统的组成

机载光电平台随动伺服系统的组成如图1所示。

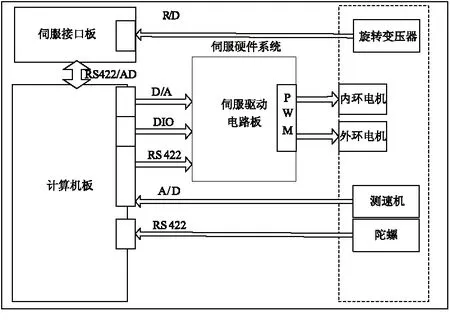
图1 随动伺服系统组成及关系图Fig.1 Composition of gimbal servo system

图1中旋转变压器为内外万向架提供角度解算信号,伺服接口板解算万向架的角度信息。陀螺和测速机为万向架的速度反馈元件。伺服驱动电路板是内外电机的驱动器。随动伺服系统的内外万向架通过AD 、DA、串口等硬件接口,在同一个计算机板内实现伺服速度闭环。

2.2 内万向架速度回路模型

内万向架速度回路采用永磁同步电机直接驱动负载做旋转运动,该子系统可简化看做双惯量模型[8],其一端为电机惯量,另一端为负载惯量。

图2中,Te为内万向架电机所产生的电磁转矩;Jm为电机转子的转动惯量;Jl为内万向架负载的转动惯量。两惯量相连接部分所等效弹簧的扭转刚度和阻尼系数分别为Ks和Bs,电机端角位置和负载端角位置分别为θm和θl。据机械结构工程师对光电平台的实测和估算,内万向架控制对象的各项参数如表1所示。

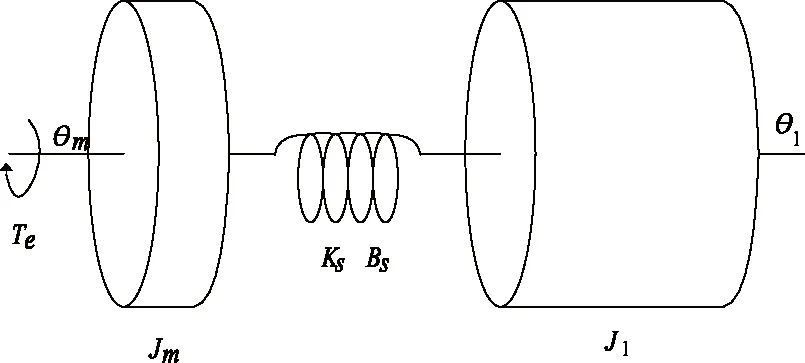
图2 内万向架双惯量模型Fig.2 Inner-gimbal two-inertia system

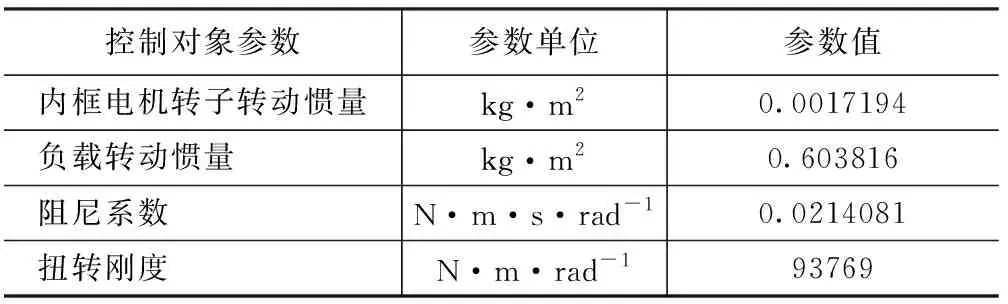
表1 内万向架控制对象参数表Tab.1 Parameters of inner plant

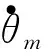
(1)

其中Jp=JmJl/(Jm+Jl)。

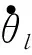
(2)

由于内万向架在外万向架的框架内搭载,启动和换向会出现内外万向架速度不一致的情况,内外万向架之间就有非线性摩擦作用,需对摩擦环节进行模型描述。Stribeck模型能较高精度近似拟合真实的摩擦力,但在其描述中静摩擦力矩是瞬间上升到最大值,与实际不符,此处对它稍作修改,使静摩擦力矩随速度按一定函数关系上升到最大。该摩擦模型表达式如下[9]:

(3)

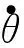
根据实际机电参数建立内万向架速度回路模型,并加入非线性摩擦模块fric如图3所示。图3中inner_cmd为内万向架速度回路的输入命令,controller为内万向架速度回路控制器,由超前和低通等校正网络组成。Motor1为内万向架电机的传递函数表达式;two-masssystem为双惯量模型;Gyro为陀螺的传递函数表达式;outer_vel为外万向架速度回路的输出角速度。

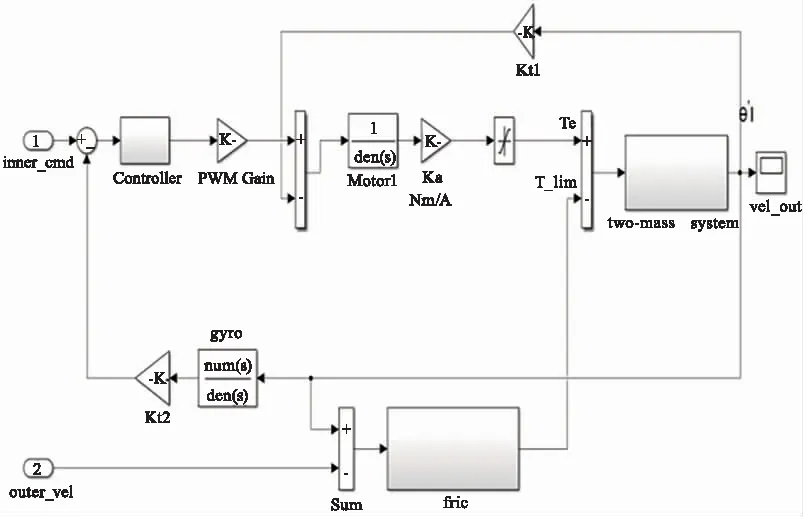
图3 有摩擦环节的内万向架速度回路模型Fig.3 Inner-gimmbal velocity loop with friction model

2.3 外万向架速度回路模型

外万向架伺服子系统的双惯量模型主要包含直流电机,减速齿轮,外万向架。具有减速机构的双惯量系统转矩方程描述如下式:

Te-Tg=Tm

(4)

Te为外万向架电机所产生的电磁转矩;Tm为作用在电机转子上的扭转转矩;Tg为电机作用在减速齿轮前端的转矩。

记外万向架电机端角位置和负载端角位置分别为Pm和Pl;电机端和负载端的阻尼系数分别为Bm和Bl;Ks为扭转刚度;N为所有齿轮传动的总减速比;Tl为作用在负载上的传递转矩;Tf为负载转矩;Jm为电机转子的转动惯量;Jl为外万向架负载的转动惯量。为简化处理,忽略中间传动部分的阻尼作用,有以下关系式:

(5)

Tg=Ks(Pm-NPl)

(6)

Tl=NTg

(7)

(8)

据机械结构工程师给出的平台外万向架控制对象参数表如表2所示。

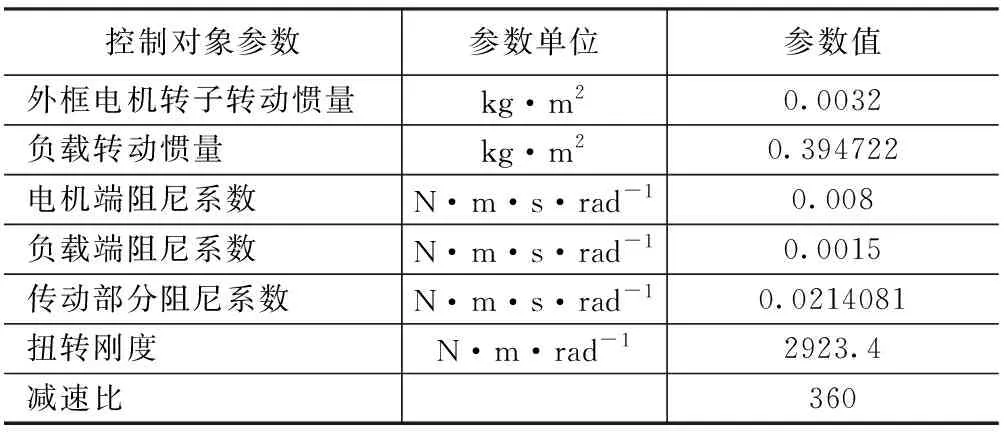
表2 外万向架控制对象参数表Tab.2 Parameters of outer plant

根据关系式(4)～(8)化简出外万向架双惯量子系统的控制框图如图4所示。

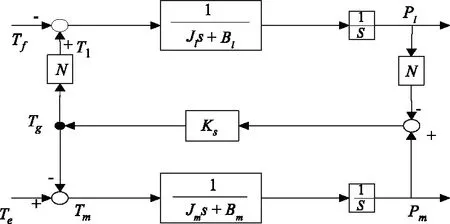
图4 外万向架双惯量模型Fig.4 Outer-gimbal Two-inertia system

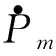
(9)

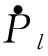
(10)

根据上述传递函数可得到外万向架双惯量系统的谐振频率fr为:

(11)

外万向架和基座之间也有非线性摩擦作用,同样采用改型stribeck摩擦模型对其建模。与内万向架不同的是,外万向架有齿轮传动部分,需要考虑电机和负载之间的传动齿隙特性,用死区环节描述该特性,表达式如下[10]:

(12)

上式中Dout为死区环节的角度输出;θ1和θ2分别为电机端和负载端的角度输出;Δ为死区宽度,k为线性部分的斜率。

采用比例超前低通等线性控制器GC(s)作为外万向架反馈补偿器,并加入齿隙环节,参考图4可将外万向架速度回路化简为如图5所示齿隙三明治系统。

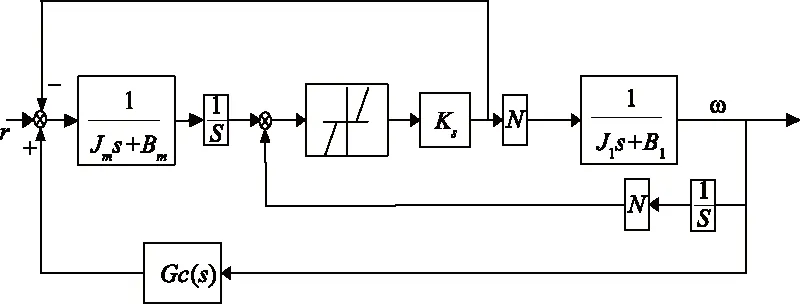
图5 齿隙三明治系统图Fig.5 System with sandwiched backlash

图5中r为速度回路参考输入,ω为输出速度。Ks为扭转刚度,它的前一级为齿隙环节,N为传递齿轮的总减速比。

2.4 内外万向架随动模型及其扫描速度曲线

2.4.1 内外万向架随动模型

内外万向架随动模型是由内万向架,外万向架的速度回路和位置回路共同组合而成。内外速度回路是内外万向架随动模型的重要组成部分,各速度回路的速度输出量值经过积分环节得到各万向架的位置变化量,并和其初始位置相加,得到内外万向架各自的最终角度位置,进而计算出系统瞄准线的角度值。根据内外万向架的交互关系以及机电相关参数搭建模型如图6所示。

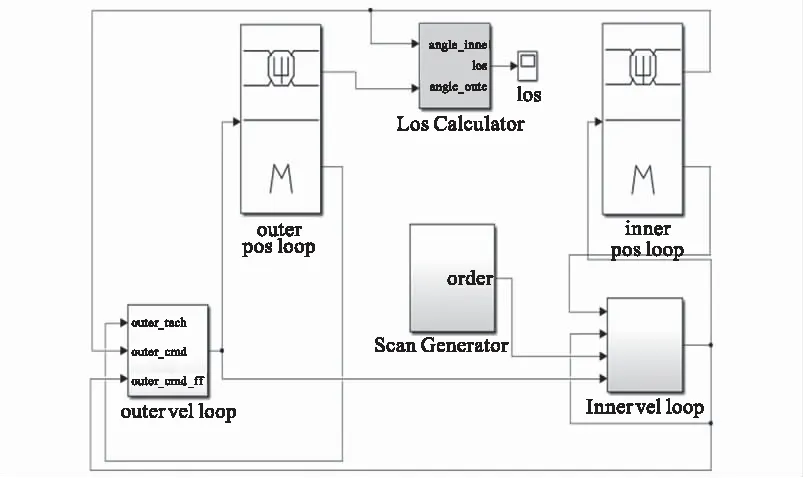
图6 内外万向架随动模型示意图Fig.6 Slave servo system of inner and outer gimbal

图6模型中inner velloop和outer velloop分别为内外万向架的速度回路,inner posloop和outer posloop分别为内外万向架的位置环,Los Calculater为瞄准线角度计算模块,ScanGenerator为扫描指令生成模块。

2.4.2 内外万向架随动模型扫描曲线

光电平台处于扫描成像模式时,其内外万向架需工作在稳速状态下。由Scan Generator模块产生的速度阶跃指令及内外万向架的速度响应曲线如图7所示。

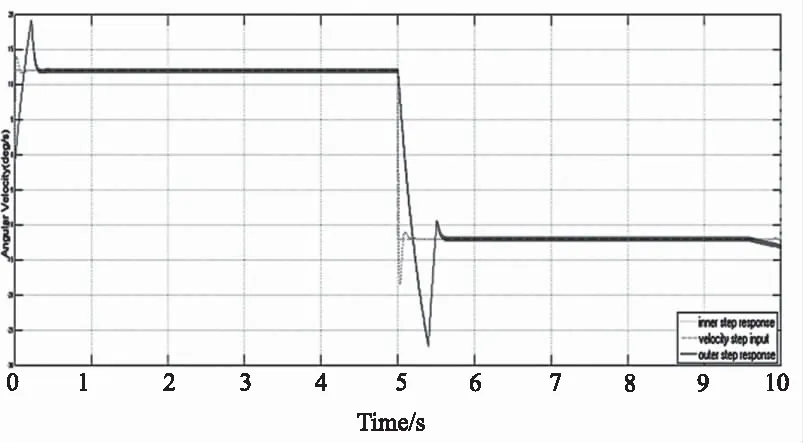
图7 阶跃指令及内外环响应示意图Fig.7Schematic diagram ofvelocity step and response

图7中速度阶跃指令的设置值为12 °/s,一个扫描周期为10 s,每经过半个扫描周期进行速度换向。内万向架通过速度闭环实现对速度阶跃指令的跟踪,其响应幅度和周期与扫描指令一致。内万向架有运动速度后,随动伺服系统生成给外万向架的随动和前馈指令,外万向架根据该指令随动于内万向架,其响应滞后于内万向架。

2.4.3 扫描稳速曲线特性小结

将内外万向架的响应曲线局部细节放大,如图8所示。

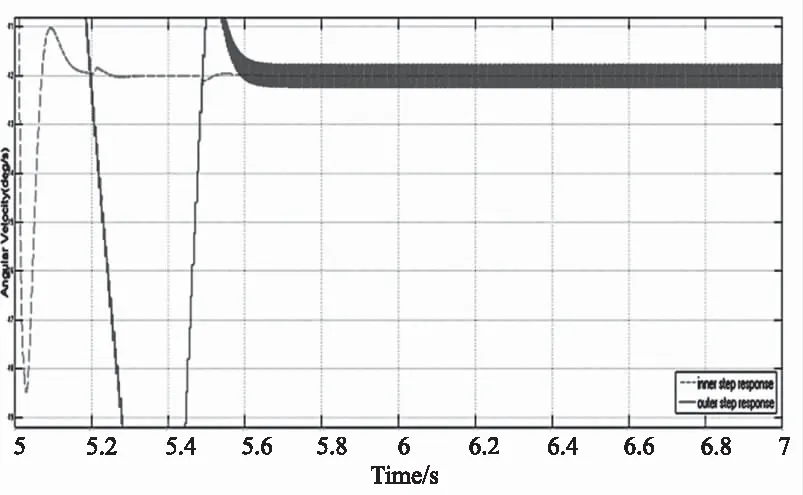
图8 内外万向架速度响应局部放大示意图Fig.8 Part response of inner gimbal and outer gimbal

图8横坐标为时间5～7 s,纵坐标范围为-19.2～-10.8 °/s,由图8可看出内外万向架在换向时超调都比较大。内万向架进入稳速区间后在5.2、5.5 s时刻附近仍有速度波动,外万向架稳速段速度波动较大,有自激振荡现象,这将对电机和平台产生不利的影响。

3 外万向架模型自振分析和动态特性优化

外万向架在随动扫描时,产生了峰峰值为0.5 °/s的速度往复速度振荡,鉴于模型外万向架速度回路的线性部分经校正后闭环极点均位于左半平面,且在模型中去掉非线性环节后振动消失,故外万向架速度振动是由非线性环节引起。

外万向架模型的非线性因素主要有摩擦和死区两种,分别去掉摩擦和齿隙两种非线性模块后,得到外万向架扫描曲线如图9所示。

图9 外万向架部分速度曲线示意图Fig.9 Partvelocity response of outer gimbal

由图9(a)和(b)部分对比可看出,去掉摩擦环节保留齿隙环节,外万向架的扫描速度振荡现象没有改变。而去掉齿隙环节保留摩擦环节,稳速段的自激振荡也跟着消失。故外万向架速度振动是齿隙环节引起。

采用描述函数方法对外万向架速度回路进行自振分析,写出代表死区特性的描述函数如下式[10]:

N(A)=

ifA≥Δ

(13)

式中,A表示输入正弦信号的振幅;Δ为死区宽度;k为线性部分的斜率。

由图5所示,围绕齿隙环节有三个并联回路,根据控制框图化简方法将其等效化简为线性和非线性两部分,化简后等效控制框图如图10所示:

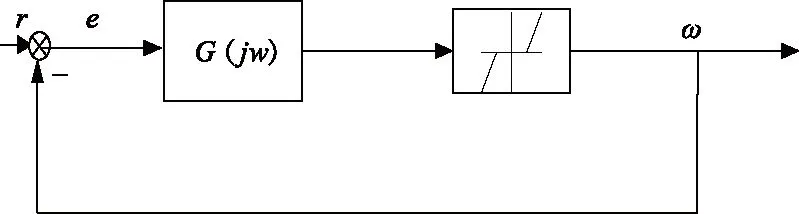
图10 含有齿隙环节的简化速度回路框图Fig.10 Simplified velocity-loop diagram with backlash

图10中非线性部分仅有死区环节。使用自控原理中的控制框图化简法,得到其线性部分G(s)的传递函数如下式:

(14)

其中GC(s)为线性控制器的频域传递函数。

在同一复平面上绘制死区环节的描述函数负倒数曲线-1/N(A)与线性部分的Nyquist曲线,局部图形如图11所示。

由图11可见,G(jw)曲线与实轴有两个交点,根据描述函数稳定性分析理论,左边的交点为其稳定的自振点,其自振动的频率为14.2 Hz。图12是仿真模型中外万向架速度曲线的局部细节图。

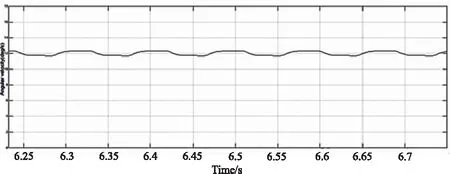
图12 外万向架速度回路阶跃速度响应Fig.12 Step response of outer velocity loop

图12中仿真响应曲线的振动周期约为0.07 s,振动频率为14.2 Hz,与描述函数法的稳定性分析化简得出的自振频率一致,表明速度仿真曲线的速度振荡是来源于齿隙环节。

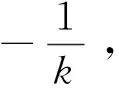
因此,要改善具有齿隙的万向架的稳速性能,可通过减小齿隙和调节负载端阻尼这两种直接的方法。当然也可使用补偿齿隙的控制方法,如逆模型、反步控制[11]和双电机消隙[12]等方法。

光电平台外万向架的直流电机加减速箱组合安装在平台基座的安装支架上,通过机械减速齿轮作用到负载上。直流电机减速箱自身的齿隙一般比机械传动齿隙要小很多,这里使用双电机消隙主要是针对机械传动齿轮进行消隙,双电机消隙的结构示意图如图13所示。

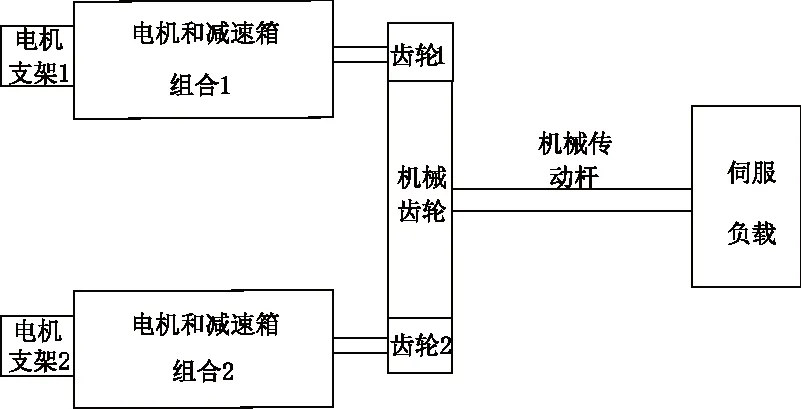
图13 双电机控制结构简图Fig.13 Structure diagram of dual motor control

根据光电平台本身的特征,采取力矩均衡式的双电机控制来抑制齿隙的非线性影响,其控制原理如图14所示。双电机力矩均衡控制,在动态时两个电机加以同样的速度指令驱动负载,驱动能力强于单电机,可解决负载较大时单电机驱动能力不足的问题。当两个电机的力矩给定值小于偏置力矩,系统处于稳态,该状态可抑制齿隙的非线性作用,加强系统的稳态性能。动态时使用两个电机的力矩差做反馈,可最终使两个电机的输出力矩趋于一致,避免两个电机相互挤压,故其动态性能也得以保证。

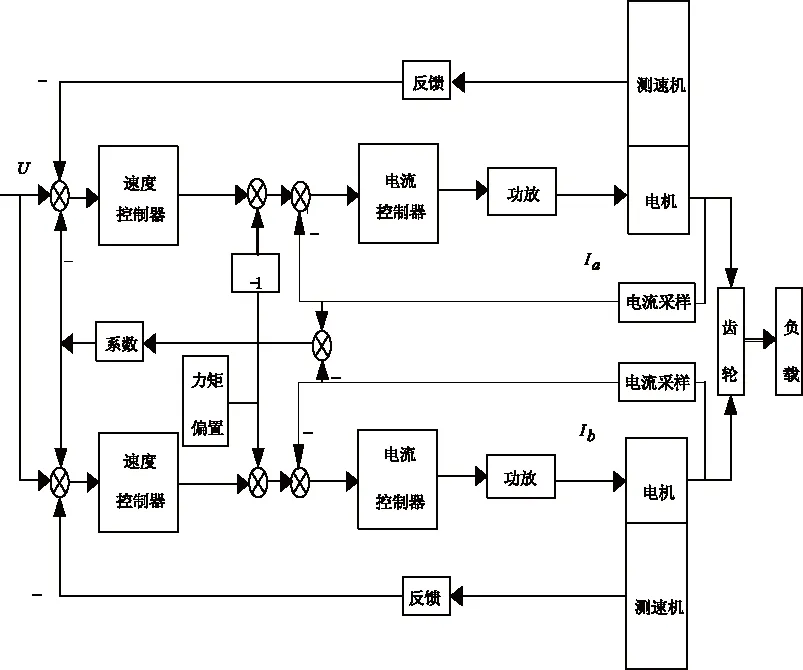
图14 力矩均衡式双电机控制原理图Fig.14 Schematic diagram of torque-balanced dual motor control

4 内万向架稳速性能和动态特性优化

4.1 内万向架扫描稳速特性的影响因素分析

光电产品的成像传感器通常安装在内万向架中,内万向架的稳速性能[13]将直接影响传感器成像的像质,故需对内万向架的扫描稳速性能进行分析和优化。

由图7可看出内万向架在换向时超调较大,且进入稳速段后,仍有速度波动,对系统的扫描稳速性能影响较大。内万向架为电机直驱系统,故不需考虑其齿隙作用,仅考虑摩擦因素。去掉模型中的非线性摩擦环节前后的对比曲线如图15所示。

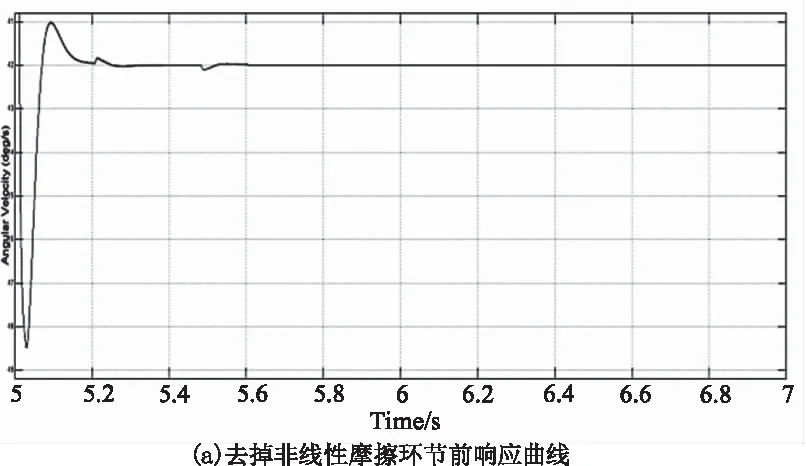
图15 内万向架局部速度响应示意图Fig.15 Part response curve of inner gimbal

由图15的(a)和(b)部分对比可以看出,去掉摩擦环节后,5.2 s和5.5 s时刻的速度波动消失。因此内外万向架之间的非线性摩擦会导致换向后仍有速度波动。

4.2 内万向架扫描稳速性能的优化

要消除摩擦作用进而提高稳速性能是不现实的,需从提高内万向架抵抗外部扰动能力的角度考虑。有许多非线性控制器可以改善摩擦带来的非线性问题,其中给速度回路加入内回路是一种简单可靠且易于实现的方法。

课题所依托的某型光电平台的内万向架驱动器无电流反馈回路,无法加入扰动观测器,故使用加速度反馈[14]的方法。采用对内万向架中的陀螺角速度信号进行微分,可从软件层面完成对加速度信息的提取,无须增加硬件成本。加入加速度反馈回路,虽不能提高速度回路的带宽,但可为速度回路提供线性度更好的控制对象,同时也可提升其抗扰能力来抑制外部的非线性摩擦作用。

根据文献资料[15-18],使用如下形式的跟踪微分器(tracking differentiator,TD):

(15)

式中,x1,x2为系统的状态变量;h为控制系统的采样周期;r0为最速综合函数控制参量,它决定系统跟踪的快慢;h0决定噪声滤波效应,它的取值一般取采样周期h的若干整数倍;v为输入信号,是需要被跟踪的角速度信号;状态变量x1可快速无超调跟踪输入的角速度信号v;而x2作为v的近似微分,代表跟踪过程的微分信号。

式(15)中,fhan(x1,x2,r0,h0)函数的表达式如下:

(16)

将角速度的跟踪微分信号作为加速度信号,在速度回路内部形成加速度回路,该回路的采样率和动态响应性能都高于速度回路,故微分器的滤波动态不会影响速度回路的稳定性。

5 平台实验验证与结果分析

5.1 内万向架加入加速度反馈后稳速曲线测试

随动伺服系统的计算机板采用PowerPC P2020芯片作为其核心处理器,在平台稳速扫描时,将角速度测量值转化为电压量并通过DA转换器输出,使用示波器测量其电压输出值。图16是使用示波器测量的系统稳速曲线。

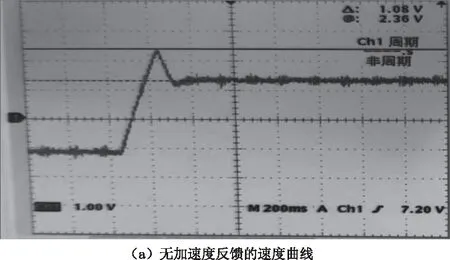
图16 测试加入加速度反馈前后的速度曲线Fig.16 Velocity curve before and after adding acceleration feedback

图16的横坐标表示时间,纵坐标表示电压值,加入加速度反馈后,扫描换向时的调节时间基本没有改变,而速度曲线的最大偏差量从1.08 V减小至1.00 V。

5.2 内万向架加入加速度反馈后隔离性能测试

加入加速度反馈能提升内万向架对非线性摩擦的隔离能力[19]。采用安捷伦HP35670A型动态信号分析仪测试其扰动隔离能力,将一定的正弦激励外万向架电流命令处,以模拟外万向架对内万向架一定量值的力矩扰动,内万向架处于速度闭环状态。以扰动信号为输入,内万向架速度信号为反馈信号,使用分析仪进行隔离数据测试,将加入加速度反馈前后一些典型频点的速度响应幅值列成表格如表3所示。

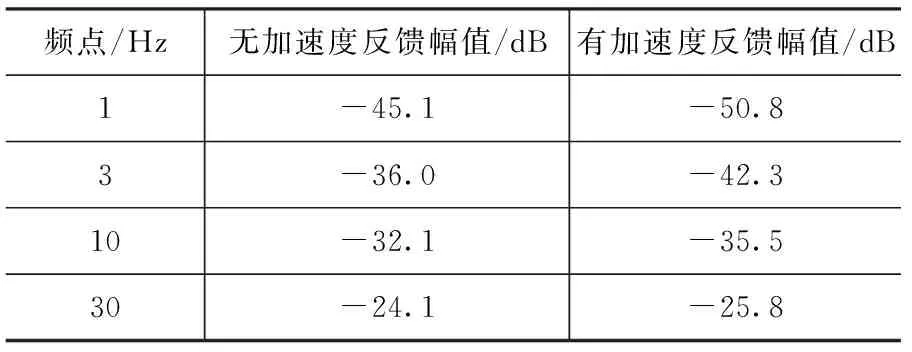
表3 扰动隔离参数表Tab.3 Parameters of disturbance isolation

由表3可以看出,加入加速度反馈后,各个频点的速度响应幅值都有所下降,即对同样的外界扰动,加入加速度反馈后内万向架的速度响应程度更低,隔离能力更强,尤其在低频较为明显。

5.3 外万向架采用力矩均衡式的双电机控制前后的稳速曲线

根据第3节的分析,非线性齿隙环节造成外万向架稳速扫描过程中的速度振荡,虽然从图8的仿真图上看,该速度振荡并未对内万向架的稳速性造成影响,但这和仿真模型中摩擦参数的设置有关,也和振荡的幅度和频率有关,要得到和实际完全一致的仿真模型很困难。在实际产品调试中,速度振荡都是系统希望避免的,抑制外万向架的速度振荡对电机或者光电产品都是有益无害的。为验证力矩均衡式的双电机控制对速度振荡的抑制效果,使用该措施前后分别采集内万向架的角速度数据,曲线对比图如图17所示。

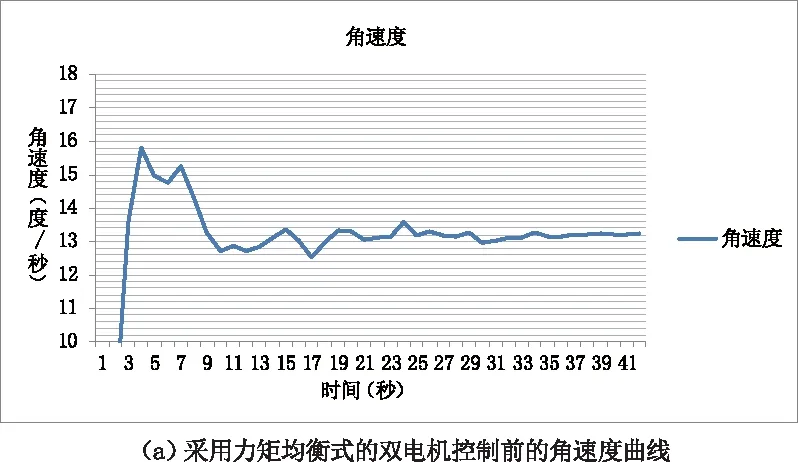
图17 采用力矩均衡式的双电机控制前后的速度曲线Fig.17 Velocity curve before and after torque-balanced dual motor control

图17中横向次网格的间隔为0.2 °/s,以给定速度13.2 °/s为中心,图(a)13秒后的稳速部分峰峰值不超过四个间隔条纹,图(b)13 s后的稳速部分峰峰值不超过两个间隔条纹。由此可知使用力矩均衡式的双电机控制后,稳速曲线更为平滑。以13.2 °/s的速度进行稳速扫描时,稳速段的速度误差的峰峰值由0.4 °/s降低为0.2 °/s。

6 结 论

以某型两轴三框架机载光电产品为依托,针对其稳速性能问题进行研究。介绍了随动伺服系统的工作原理,根据其原理建立仿真模型,并使用模型探寻其稳速性能的关键影响因素。在定位是齿隙因素造成的外万向架速度振荡后,使用描述函数法计算得到齿隙造成的自激振荡频率,并给出了减小齿隙因素影响的途径。明确了摩擦环节对内万向架的稳速性能的影响,通过实验验证,在内万向架速度回路中加入加速度回路。减小了内万向架扫描换向时的超调量,提高了内万向架稳速扫描时的抗扰动的能力,在外万向架采用力矩均衡式的双电机控制,减小了平台稳速扫描的速度误差,提升了平台的稳速性能。