基于图像的输电线路下垂检测
傅川岳, 高德民, 黄楷敏, 徐刚
(深圳供电局有限公司, 广东, 深圳 518001)
0 引言
在输电线路中,导线悬挂在2个连续的杆塔上,其重量导致导线下垂。输电线路的下垂剖面取决于导线单位长度的重量、电缆中的水平张力和安装点的高度。覆冰、风流、温升、电流等环境条件使导线发生拉伸,导致电缆下垂加剧。夏季高负荷输电线路的垂度比冬季高出许多,下垂会将导体降低到离地不安全的高度。因此,了解导线的下垂特性对导线的设计和使用寿命具有重要意义。通过精确测量导线的下垂度,可以相应地测量导线的温度[1-2],一旦获得下垂度和温度,就可以计算线路的载流量[3-5]。利用图像处理、激光技术、GPS、倾斜传感器等协调方法,可以直接测量下垂电缆的轮廓。也可以通过使用传感器[6-8]测量导线的张力、温度和周围磁场,并将测量参数与电缆下垂相关联来计算。然而现有的这些方法存在花费大、测量复杂等问题[9],因此本文提出图像处理方法,直接提取下垂轮廓。该方法通过无人机获取电线图片,然后利用公式进行相应的推算,实现对电缆下垂弧长的估算。
1 无人机图片获取
首先通过无人机对输电线路进行图片获取,需要利用无人机对输电线路进行拍摄,在获取图片后,对图片进行预处理,以满足后续分析的需要[8-9]。
第一步是对图片进行去噪处理,只保留有用部分。然后对图像进行颜色空间转换[10],由彩色图片转换为黑白图片,如图1所示,方便后续分析需要。

(a) 无人机拍摄的原画面
2 铰接缆索的静力分析
在下垂问题中,一个具有预定质量和长度的均匀柔性弦悬挂在两端。图2为下垂剖面,其中绳索的端点由A和B表示。弦可以是链、弦、绳或传输线中的导体。本文讨论了在高压电力线路中传输电能的电缆,将其视为电缆。电缆端部的固定点可以彼此处于不同的垂直水平和水平距离。可以将下垂电缆的形状被认为是悬链线。本文所考虑的拉索垂度计算方法是根据上述几何参数和张力参数,求出拉索垂度曲线的数学表达式。
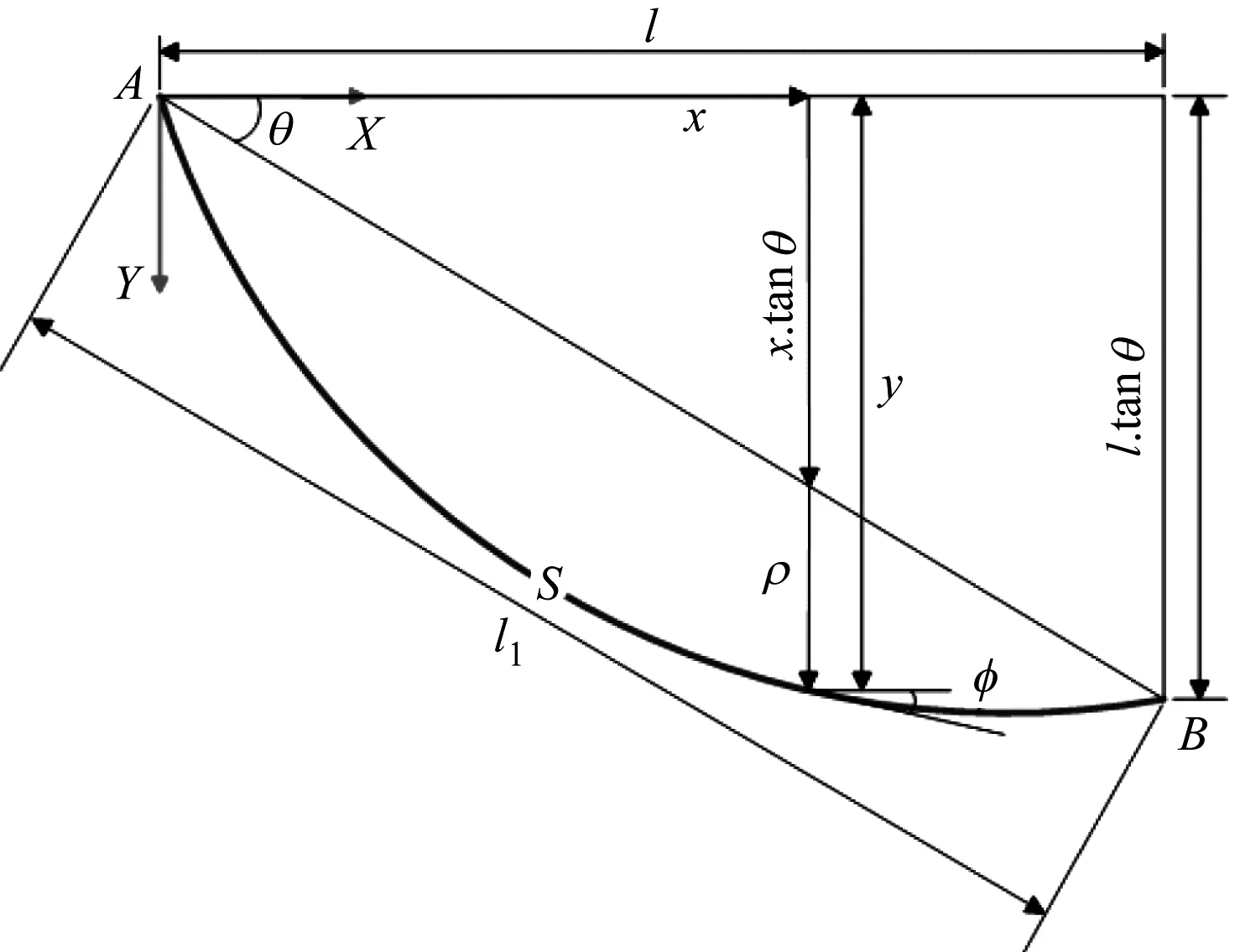
图2 悬索
为了推导长度为S的均匀电缆的下垂剖面,将A点看作坐标系的原点。坐标系Y轴的正方向沿重力方向,电缆长度沿X轴增加。跳线跨度定义为连接电缆两端支承端的线电缆,用z表示,跨线相对于水平轴的角度测量为θ。属于绳索的任何点的位置可以用上述的笛卡尔坐标表示。表示电缆剖面的另一种方法是使用体坐标。其中,第一个分量s表示电缆长度,从电缆的起点A点开始,到电缆上的指定点结束;另一个分量是指定点处电缆剖面相对于水平线的角度。
如图3所示,通过考虑缆索的无穷小单元来提取缆索的控制方程。通过忽略作用在节段截面积上的剪力和力矩,唯一的力是缆索的重力和内张力。
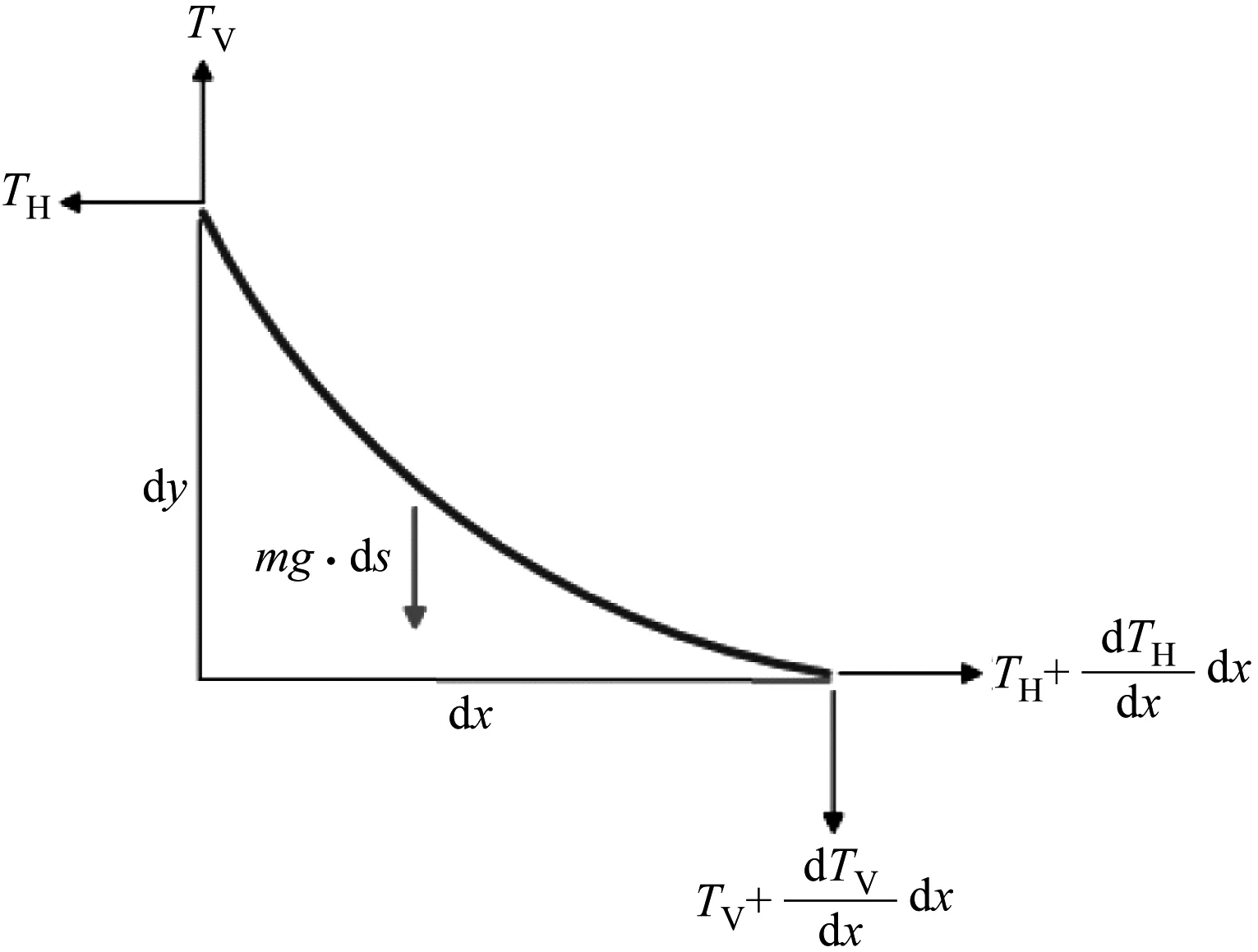
图3 无限小电缆段
沿坐标轴从力平衡方程得出式(1)、式(2):
(1)
(2)
其中,式(1)表明水平索张力在索剖面上是恒定的。由于张力单独作用于电缆剖面,水平和垂直分量之间的关系如式(3):
(3)
电缆的无限小长度可通过式(4)获得:
(4)
将式(3)和式(4)代入式(2),得到电缆剖面的微分方程如式(5):
(5)
利用式(5)相应的边界条件,得出电缆剖面的数学模型如下:
(6)
式中,a和β是参数,定义如下面的式(7)、式(8):
(7)
(8)
结合上述方程并沿电缆长度积分,得出电缆长度为x的函数,如式(9):
(9)
利用该方程,索力TH的水平分量为式(10):
(10)
该方程有3个解,第一个解为零,另外两个解的大小相同,符号相反。由于索的张力不是零,也不能是负的,所以正解被认为是正确的答案。
3 实验装置
实验装置由一个固定的1 m×1 m正方形框架组成,框架的两个垂直侧面安装有线性导轨。两端栏杆上固定一根长度为1.28 m的均匀电缆。缆绳的两端通过旋转接头连接在两根栏杆上,缆绳在两端可以自由旋转。线性导轨提供了将电缆端部设置在不同高度和跨度的能力。两个圆盘连接在电缆的两端,中心在两端(图4)。由于实验的背景色为白色,因此选择磁盘和电缆本身的颜色时,应确保与背景形成适当的对比。为了获得电缆剖面的图片,摄像机被固定并相对于框架进行校准。该相机的图像分辨率为640×480,在帧中心使用一个预定义的矩形形状,得到缩放因子。已知电缆点的像素坐标,计算电缆点的长度坐标。实验参数见表1。

表1 实验参数

图4 实验装置
获取电缆上点的坐标的第一步是提取电缆剖面。对于电缆的特定配置,从图5拍摄的图像中提取电缆的轮廓。参考图5可以清楚地看到,图像处理过程没有完全提取电缆的形状,该方法的可靠性取决于周围环境的亮度以及电缆本身与背景的对比度。

图5 提取的电缆剖面的二值图像
4 结果讨论
为了获得电缆轮廓的坐标,使用提取轮廓的二值图像。如图5所示,由于电缆的厚度,对于沿电缆的特定长度,可将几个点视为电缆坐标的代表。因此,沿厚度方向的中点被视为电缆剖面的坐标。由于图5的轮廓没有均匀的厚度,因此计算出的轮廓不是平滑曲线。为了将图像处理程序的结果与该分析方法进行比较,所获得的任一方法的轮廓如图6所示。在电缆底部点两侧提取的剖面之间存在一些偏差。

图6 实验结果与解析解的比较
为了澄清所获得的结果,分析剖面和实验剖面之间的误差曲线如图7所示。根据图7,最大误差约为电缆长度的0.045,最小误差在电缆剖面的最低水平附近,并沿电缆两侧的长度增加,直至到达电缆锚定点附近。通过在底部点两侧沿电缆长度移动,电缆剖面的倾斜度增加,从而导致电缆的截面积沿垂直方向增加。因此,代表电缆剖面点的数量增加,在这些区域中会有更多的偏差。

图7 误差曲线
由于通过图像处理提取的电缆截面轮廓不是一条光滑的曲线,其结果不适用于直接测量电缆的长度。因此,为了计算电缆长度,需要对数据拟合平滑曲线。为了使曲线与电缆剖面的实验数据相吻合,检验了解析无量纲式(3)。将图像处理方法提取的电缆截面轮廓的400个点归纳到式(6)中,得到电缆截面轮廓的实验解析解。实验分析剖面的参数如表2所示。

表2 无量纲参数
为了比较不同解决方案的结果,图8提供了3种方法获得的下垂曲线。如图8所示,实验解析解大致位于另2个解的区域内。利用实验解析解的尺寸参数,可以用式(9)计算下垂电缆的弧长。

图8 解析、实验和实验解析解
5 总结
本文研究了一种基于图像处理的下垂轮廓提取方法的实现。通过将实验结果与悬链线形状分析方法的结果进行比较,证实了图像处理方法是一种很有前途的获得下垂导线轮廓和最低水平的方法。由于该方法直接提取电缆点的坐标,因此比基于磁场法或力觉法等易产生高压的显式弧垂测量方法更易于处理。使用该方法,可以提取整个电缆剖面的坐标并相应地测量电缆长度,而不是像激光技术、倾斜传感器和GPS这样的点对点协调方法,在这种方法中,为了计算下垂剖面的形状,需要分析感测数据的集合。

