城市边缘区域多轨道站点接驳公交线网优化设计

袁 蕊,马新露

（重庆交通大学 交通运输学院,重庆 400074）

0 引言

城市边缘区处于城乡交汇地带，其用地属性方面与城市中心区有较大差别，城市边缘区域轨道线网往往比较单一、客流量相对较少，边缘区内居民出行“最后一公里”问题突出。因此，对城市边缘区内多轨道站点的接驳公交网络设计具有较大现实意义。

轨道接驳公交网络优化研究是近些年来的热点研究之一，从公交接驳轨道站点数量来说，大致可分为单轨道站点接驳公交及多轨道站点接驳公交两类。赵腾菲等[1]以公交运营收入最大化为目标，构建了接驳单轨道站点的循环社区公交网络优化模型。熊杰[2]等以路径需求潜力最大化为目标，对社区公交接驳单轨道站点路径进行优化设计。马壮[3]、张钰雪[4]以乘客需求最大化及行程时间最小化为目标构建接驳单轨道社区公交模型，上述学者皆采取启发式算法求解模型。Cao[5]、Deng[6]、王志美[7]等均以乘客成本与公交运营成本之和最低为目标，构建线形多轨道站点接驳公交模型并皆采用遗传算法求解模型。车辆路径优化问题（vehicle routing problem，VRP）求解一直是重难点问题，该研究构建了考虑轨道站点与接驳公交线路“多对多”模式的循环接驳公交网络模型，并设计遗传算法求解模型。

1 接驳公交线网优化模型

1.1 问题及假设

该文将城市边缘区域内各换乘需求点作为备选公交站点，并依据公交站点数量、线路长度、多对多等约束，设计接驳公交网络，并做出以下假设，同时为构建接驳公交网络模型，对模型参数与变量标定如表1所示。

表1 模型参数表

（1）接驳公交均采用同一车型，且在行驶过程中公交行驶速度相同。

（2）每个公交站点仅能服务一条公交线路。

（3）公交开行时，乘客均已到达各公交站点候车。

（4）每条接驳公交线路至少接驳一个轨道站点。

1.2 模型构建

1.2.1 目标函数

该研究以接驳公交网络广义总成本最低为目标函数建模，网络总成本由乘客出行时间成本以及公交运营成本两部分构成，则两类成本具体构成如下。

（1）乘客出行时间成本。乘客出行时间主要由乘客候车时间及乘客乘车时间构成，则乘客出行时间成本如式（1）所示：

式中，T、B、K分别表示轨道站点、公交站点及接驳公交数量的集合。

（2）公交运营成本。公交运营成本主要由公交运行里程数、公交单位里程运营费用及公交发车频率三者之积构成，其成本构成如式（2）所示：

式中，R表示轨道站点与公交站点集合。

（3）接驳公交网络总成本。接驳公交网络总成本目标函数由乘客出行时间成本及公交运营成本之和构成，其成本如式（3）所示：

1.2.2 约束条件

约束条件1：线连通性约束。

该约束要求每条公交线路至少应包含一个公交站点、一个轨道站点；每条公交线网的起终点均为轨道站点；每条公交线路可连接多个轨道站点，即轨道站点与公交线路“多对多”模式。

约束条件2：公交线路发车满载率约束。

该约束要求公交载客量不得超过公交容量，其满载率需在满载率上下限区间范围内，约束如式（7）所示：

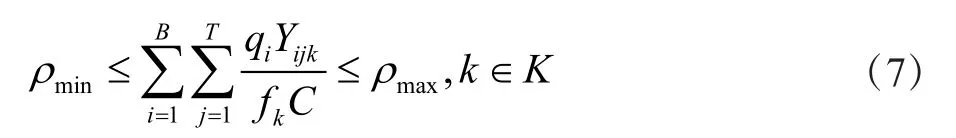
约束条件3：公交线路长度约束。

该约束要求公交线路长度范围需在接驳公交设计长度范围内，约束如式（8）所示：

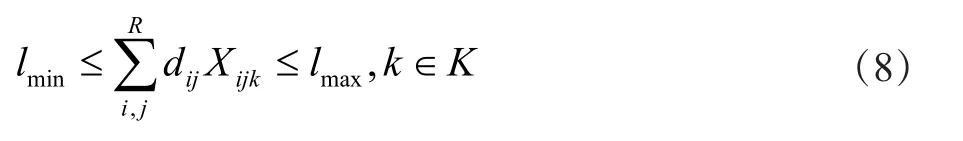
约束条件4：公交发车频率约束。

该约束要求接驳公交发车频率应符合接驳公交发车实际情况，约束如式（9）所示：

约束条件5：运能匹配约束。

该约束要求接驳公交应该满足乘客换乘需求，单位时间公交发车频率需满足单位时间内乘客的换乘需求，约束如式（10）所示：

约束条件6：公交站点需求约束。

该约束要求公交线网中，每个公交站点的乘客出行需求仅能分配至一条公交线路，且要求所有公交站点的乘客出行需求被分配至各条线路，约束如式（11）～（12）所示：

约束条件7：公交站点数量约束。

若接驳公交线路的车站数量太多，则会增加绕行距离和旅行时间，若太少则会影响客运量，约束如式（13）所示：

约束条件8：决策变量约束。

接驳公交路径优化网络模型中的0-1决策变量如式（14）所示：

2 实例分析

2.1 案例概况

大学城区域现有公交线路多，致使区域内线路复杂、线路冗余，同时片区既有公交站点中仍有部分站未与轨道站点接驳，导致部分站点乘客换乘轨道的需求无法满足。该案例以现有公交站点为备选公交站点，包含轨道站点共计17个站点，对轨道站点编号1-2，公交站点编号3-17。

于大学城区域内实地调研各换乘公交站点的高峰时段内乘客出行需求数据并通过高德地图获取站点间距数据。

2.2 模型求解

设计遗传算法求解接驳公交网络优化模型，设置并输入相关参数以便求解模型，其中算法相关参数有：种群大小pop=20，迭代次数Maxit=500，代沟GAPP=0.9，交叉概率Pc=0.9，变异概率Pm=0.05。使用MATLAB R2016b软件求解。

接驳公交网络模型参数标定结果为：lmin=2 km、lmax=8 km、fmin=4 min、fmax=20 min、λ=10 元 /人 * 小时、C=40 人 / 辆、Vbus=15 km/h、ρ=40%、ρ=100%、Nmax=16、Cm=25元/km。

设计遗传算法求解模型，求解结果展示分别如表2、图1所示，对优化前后效果对比如表3所示。

表2 遗传算法求解结果

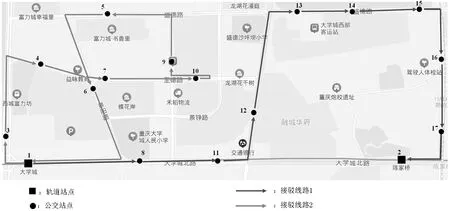
图1 大学城片区接驳公交线路优化设计

表3 优化前后大学城片区公交对比

由表3可知，优化后的接驳公交网络可完全覆盖片区内需求点，且接驳线路相较于规划前更为科学、合理。

3 结论

该文结合现有轨道接驳公交网络优化研究，考虑多轨道站点的接驳公交网络设计，构建多对多模式下的环形接驳公交网络优化模型并设计启发式算法求解，可得以下结论：

（1）既有研究中关于多轨道站点的循环接驳公交网络优化研究较少，该文多对多约束下，以公交线路结构、发车频率以及公交接驳公交数量为变量，构建多轨道站点循环接驳公交网络，并通过算法求解验证其可行性。

（2）考虑乘客出行成本及公交运营成本之和的广义出行总成本目标函数，乘客出行成本占比更大，算法迭代求解则侧重乘客出行成本优化。因此，基于公平原则下的乘客出行成本和公交运营成本的协同优化需进一步研究。