尺寸效应对混凝土试块抗压强度的影响
周齐洪 张泽宇 唐 莉 杨 畅 彭 昊
(1.四川农业大学建筑与城乡规划学院,四川 都江堰 611830;2.重庆市建设工程质量检验测试中心有限公司,重庆 400016)
关键字:混凝土;尺寸效应;试块抗压强度;强度转换;高强材料
0 引言
混凝土试块截面尺寸的增加造成混凝土试件抗压强度的降低,是混凝土尺寸效应的普通表现。既有研究发现,随着材料强度的提升,混凝土立方体试块抗压强度的尺寸效应越明显[1-3]。尤其是C60以上的高强混凝土,尺寸效应造成的立方体抗压强度折减比例会显著提升[4]。苏捷[5]试验研究发现,随着截面宽度的增加,棱柱体的轴心抗压强度逐渐变小,且提升材料强度会加速试块抗压强度的衰减。日本学者[6-7]在混凝土圆柱体试块抗压强度的试验研究中也获得类似的结论。
既有研究还发现,混凝土试件的长宽比同样会引起尺寸效应[8]。Mansur等人[9]发现,随着材料强度的增加,同截面尺寸的混凝土圆柱体与立方体抗压强度比也随之增加。过镇海[10]通过对已有122组数据统计分析,发现混凝土的轴心抗压强度随立方体抗压强度单调增长,且两者比值的变化范围为0.70~0.92。然而,宋中南[11]认为,长宽比对试块强度的影响主要表现在80MPa以下的试块强度范围;当材料强度在100~120MPa范围,100mm的立方体抗压强度fcu,100与圆柱体强度fcy,100差异不再明显。
因此,试块尺寸和强度等级均是尺寸效应对混凝土抗压强度影响的重要因素。但不同学者在主控因素对混凝土试块,尤其是高强(高性能)混凝土,抗压强度的具体影响趋势及量化建议上仍存在一定差异。
本文收集1107组既有混凝土试块试验数据,通过数理统计回归分析方法,系统地研究了现行相关规程与学者既有成果在混凝土试块抗压强度计算与转化方法上的精度与可靠性,并重点分析了高强度混凝土的试块抗压强度计算方法。
1 试验数据及特征分析
基于国内外既有文献资料[2],[9],[12-36],本文将整理的1107组混凝土试块试验数据整理成样本库,其中包括了四种试块类型(边长为100mm与150mm的立方体,150mm×150mm×300mm的 棱 柱 体 及Φ150mm×300mm圆柱体)及对应的抗压强度。样本库的抗压强度范围约在18.2~128MPa。
图1以标准立方体试块为中介,对4种试块类型进行分类统计,获得了标准立方体试块与其他3种试块类型的3项配对数组。以fcu,150≥60MPa的样本标定为高强混凝土,则各类规格的高强试块均约占各自占比的50%或以上。
2 不同混凝土试块抗压强度的转化方法
2.1 混凝土试块抗压强度的转化方法
本文共采取了7种相关规范及学者提出的针对各类试块的强度转化方法及其适用范围,包括规程《高强混凝土结构技术规程》(CECS 104:99)[37]和《混凝土结构设计规范》(GB 50010-2002)[38]中的换算公式与高志扬[2]、Peterson[39]和马欣伯[40]各自所使用过的换算方法。
高志扬:

Peterson:

马欣伯:
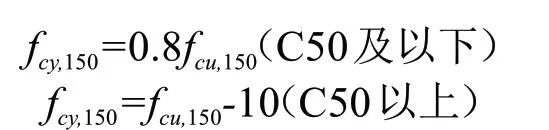
其中马欣伯的建议方法是综合了欧洲规范与美国规范的优化方法。除了国内规范出于实用性考虑分段系数法外,上述所采取的试块抗压强度转换方法基本满足了函数的连续性。对于样本数据中部分超出推荐方法的适用范围的高强试块,转换方法参考C80转换系数值。
2.2 立方体试块之间抗压强度的转换方法
基于样本库a组中100mm与150mm立方体的377组实测数据,依据CECS 104:99规程与高志扬建议的立方体试块间抗压强度转换方法,分别讨论两种转换方法下的立方体试块强度转化精度。
由图2不难看出,针对fcu,150向fcu,100的转化,当偏差在±15%之内时,CECS 104:99规程和高志扬方法的数值占比相当,两种方法的计算值与试验值总体上偏差均不大,均值与方差整体水平基本一致。
进一步通过对高强试块间的强度转化精度进行对比分析可以看出,CECS 104:99规程与高志扬方法在±15%内偏差分布特征类似,但高志扬方法的精度更高。
2.3 棱柱体与标准立方体抗压强度的转化方法
依据CECS 104:99规程与GB 50010规程的转换方法,针对b组中120组实测数据,以标准立方体抗压强度实测值fcu,150-exp计算出相应的150mm×300mm棱柱体试块强度fc,150-cal,将其与对应的实测值fc,150-exp进行对比。
由图3可以看出,CECS 104:99规程基本满足fc,150-cal/fc,150-exp在±15%之内,而GB 50010规程的计算值评估整体偏保守。研究高强范围内尺寸效应对混凝土试块抗压强度影响,基于CECS 104:99规程的高强样本数据随fc,150-cal/fc,150-exp比值呈正态分布,偏差±15%以内的数据占比97.3%。GB 50010规程除了计算值保守外,仅有75.7%的数据偏差在±15%以内。
综上所述,CECS 104:99规程的推荐方法更适合用于标准立方体与棱柱体之间的转化。
2.4 圆柱体与标准立方体抗压强度的转化方法
依据CECS 104:99规程、马欣伯及Peterson推荐的转换方法,针对c组中57组实测数据,以标准立方体实测值fcu,150-exp计算出相应的圆柱体抗压强度计算值fcy,150-cal。
以±5%偏差率为梯度,图4统计了各偏差率内的数据分布特征。不难发现,Peterson方法的整体均值、方差、偏差±15%内数组占比均为最优,其次为马欣伯推荐方法,CECS 104:99规程整体表现相对最差。针对高强试块,虽然3种推荐方法的转化精度均有所提升,但Peterson方法仍具有最优均值和最佳稳定性。
基于上述分析结论,选取15%以内保证率最高的换算方法,可确定:立方体试块间抗压强度转换方法、棱柱体与标准立方体抗压强度转化方法均采用CECS 104:99规程,标准圆柱体与标准立方体抗压强度转化方法采用Peterson推荐方法。
3 尺寸效应对混凝土抗压强度的影响
图5中的离散点展示了a、b、c三类试块分组的实测比值与试块强度之间的关系。
由图5可以看出,随试块尺寸或体量的增大,各比值呈逐渐减小的趋势,同时,随着材料强度的提升,圆柱体和棱柱体的强度衰减程度更明显。Peterson方法和CECS 104:99规程分别在立方体与圆柱体之间、立方体试块间的抗压强度转化基本满足该规律。而CECS 104:99在进行标准立方体与棱柱体抗压强度转化计算结果方面,保证的是最小包络线,即fcu,150对fc,150的转化结果偏保守;尤其是C50以上的强度转化规律呈现随材料强度的提升转化系数逐渐增加趋势,这与工程实际情况存在差异,有必要进行修正。针对C50以上的立方体和圆柱体实测数据进行数据回归分析,如图5中虚线所示,依据转化系数随材料强度的变化趋势,本文建议fcu,150与fcy,150的转化方法采用下式计算:

4 结束语
基于4种不同类型的混凝土试块实测数据,本文分别对比分析了现行规范及学者提出的试块强度转化方法的精度和适用性,并提出了C50以上标准高强立方体试块与对应棱柱体试块的抗压强度转化公式。
同时,分析了试块尺寸、形状等因素对强度指标的尺寸效应影响规律,具体如下:
(1)材料强度的提升及混凝土试块体量的增加,均将引起试块抗压强度的衰减,其中试块高宽比的增加造成抗压强度衰减更明显。
(2)《高强混凝土结构技术规程》(CECS 104:99)规程和Peterson推荐方法分别在立方体试块间抗压强度转换精度、标准立方体和棱柱体抗压强度转化精度上表现最佳。
(3)相比《混凝土结构设计规范》(GB 50010-2002)和《高强混凝土结构技术规程》(CECS 104:99)在标准立方体与棱柱体抗压强度转化精度和稳定性上更佳,但两者在高强材料的转化精度上均有缺陷。

