基于格的口令认证密钥交换协议综述

郭渊博，尹安琪

（信息工程大学密码工程学院，河南 郑州 450001）

0 引言

近年来，随着5G、云计算、大数据、人工智能等高新技术的飞速发展，人类的生产、生活也随之走向深度的信息化、网络化、数字化。以“互联网+”为代表的新型发展生态已经成为中国社会发展的国家战略。由于网络的开放性与匿名性，互联网在快速发展的同时衍生出一系列安全问题，网络空间俨然成为国家安全的“第五疆域”[1]。身份认证系统是保护网络资产过程中的重要关卡[2]，一旦其被攻破，信息和网络系统内所有的安全措施就形同虚设。

基于口令的身份认证技术不存在高熵密钥的管理问题（相比基于智能卡、U 盾等信任物体的身份认证技术），也不存在用户不可撤销的隐私泄露问题（相比基于指纹、虹膜等生物特征的身份认证技术），大大降低了认证成本并提高了安全系统的便利性、可部署性。然而，与已经得到深入、广泛研究的高熵密钥认证方式相比，口令认证的研究成果相对不足。口令认证作为一种低熵认证方式，虽然曾一度因各种安全问题被认为必将消亡，但迄今为止，口令认证仍是各类信息和安全系统中应用最广泛的认证方式之一[3]。由于口令认证是唯一不需要进行硬件部署的认证方式，在绝大多数网站中，基于口令的单因子认证方式无可替代[1]。口令在工业界的作用也从未淡化，其不仅在传统的电子政务、商务、医疗等领域继续发挥优势，还向交通、税务、广电、能源、水利、教育等多领域不断扩展[4]。虽然在2022 年MIT Technology Review“十大突破性技术”[5]掀起了“终结口令”的第二次浪潮，但汪定等[3]指出，无口令身份认证方案目前存在兼容性差、可扩展性低、成本高和存在隐私泄露等风险，并特别指出无口令身份认证方案降低了用户对身份的控制权，因而有52%的被调研者并不接受此类认证方式。因此，学术界与工业界逐渐达成共识，在可预见的未来，口令认证仍将是用户最主要的认证方式之一[1,3,5]。

现阶段，口令认证的相关研究聚焦于设计适用于不同应用场景的安全高效的口令认证密钥交换（PAKE,password-authenticated key exchange）协议。PAKE 协议使只拥有低熵口令的协议参与方可以通过非安全信道协商用于安全通信的高熵密钥[6]。研究者先后提出了一系列PAKE协议[7-13]，如著名的SPR[7]、PAK[8]、PPK[9]、KOY/GL[10-11]和JG/GK[12-13]协议。上述协议都是基于传统困难问题的，但早在1994年Shor[14]就证明，存在量子算法可以解密所有基于大整数分解和离散对数等传统困难问题的密码体制，且量子计算机已经诞生[15]，其量产化和实用化只是时间问题。因此，基于传统困难问题的PAKE 协议在即将到来的量子时代不再安全。

为应对量子攻击，密码学者已经开始研究各种抗量子的密码体制。除了以AES、DES 为代表的对称密码体制外，现有公认的抗量子密码体制主要分为以下5 类[16-17]：基于哈希的密码体制[18]、基于编码的密码体制[19]、基于多变量的密码体制[20]、基于格的密码体制[21]和基于同源的密码体制。其中，基于格的密码体制有以下优势：1) 密码学者已经完成了格上部分困难问题从平均情况下困难性到最坏情况下困难性的归约证明[22]，因此基于格的密码体制不仅具有更强的安全性，在应用时还支持困难实例的随机选取[22]，这也是此类密码体制独有的优势；2) 格上的运算一般具有线性渐近复杂度，如小整数的矩阵、向量的模乘/加，而基于大整数分解和离散对数等传统困难问题的密码体制需要采用大整数模/幂运算，相比之下基于格的密码体制具有高效性[23]；3) 格上有多个困难问题被证明是困难的，如最短向量问题、最近向量问题、带差错学习问题，这为基于格的密码体制提供了丰富的密码学原语选择空间[16]；4) 鉴于格的简单代数和几何结构，基于格的密码体制易于通过软件和硬件实现[17]；5) 密码服务功能较强，在全同态加密[24]、多线性映射[17]等领域具有广泛的应用前景。因此，基于格的密码体制被美国国家标准与技术研究院（NIST）认为是后量子时代最具潜力的密码体制[25]。

然而与已经得到深入研究和广泛应用的传统密码体制相比，关于基于格的密码体制的研究相对不足。当前，相关研究主要集中在加密算法和哈希函数2 个领域，关于格上PAKE 协议的研究成果还比较有限。随着网络和信息技术的快速发展，各方对大规模通信系统中的身份认证方案需求日盛；但格上相关方案的执行效率较低，且个别方案仅实现了密钥传输。另一方面，目前格上PAKE 协议的研究多关注如何提高单服务器PAKE 协议的执行效率，此类协议固有的缺陷是无法抵抗服务器泄露攻击；个别可抵抗此类攻击的相关方案未实现唯口令设置和密钥交换，且执行效率低下。

早期协议的研究基于启发式安全性分析，这使协议研究一度陷入了“提出→攻击→改进→攻击→改进”的循环[1]。因此，可证明安全逐渐成为必要的设计目标。PAKE 协议的研究也由此衍生出以下2 条技术路线：在随机预言机模型（ROM,random oracle model）/理想加密模型下最优化PAKE 协议的性能[9,26-28]；在标准模型下，构造可证明安全的高效PAKE 协议[13,29-33]。相比之下，在标准模型下构造可证明安全的PAKE 协议更加困难。然而，在格PAKE 方案中使用随机预言机比在一般方案中更具安全威胁，主要原因如下：随机预言机的安全性本身存疑，因为在实际应用时随机预言机需要被具体的哈希函数替代[34]；对于PAKE 协议而言，使用随机预言机还可能导致协议遭受离线口令猜测攻击；格密码方案的主要应用场景为后量子时代，量子敌手可以在量子态下访问随机预言机[35-36]，这进一步加剧了使用随机预言机对格PAKE 方案的安全威胁。因此，在格PAKE 方案中应尽量避免使用随机预言机，这使基于格假设构造PAKE 方案更加困难。

PAKE 协议还面临离线口令猜测攻击、在线口令猜测攻击和各种新型口令猜测攻击的威胁[1]。抵抗离线口令猜测一直是PAKE 协议设计的重点与难点[13,37]。当前，口令泄露问题日益突出，2021 年，仅RockYou2021 数据集就泄露了84 亿条口令记录。知名网站（Yahoo、163 等）、社交媒体（Facebook、Instagram 等）、营销服务提供商（大众、奥迪等）也都发生过口令泄露问题，且口令泄露在短期内往往难以被发现，这进一步加剧了口令泄露的危害。相比之下，在进行在线口令猜测时，攻击者无法获得用户口令文件且可执行的猜测次数受限，因此无论是在学术界还是在工业界，在线口令猜测一直被认为是易于防范的[11,36]。但事实是用户与服务器商正遭受日趋严重的在线口令猜测攻击，如Github 和iCloud 等知名网站都遭受过此类攻击。Wang 等[38]指出当前的研究大大低估了真实攻击者在线口令猜测的成功率。此外，随着网络化、信息化、数字化的深入发展，还涌现出一系列新型口令猜测攻击，如基于深度学习的[39]和基于云计算增强的[40]口令猜测攻击等，这导致PAKE 协议面临更加严重甚至未知的安全威胁。另一方面，《“十四五”规划和2035 年远景目标纲要》明确指出要“加强重要领域数据资源、重要网络和信息系统安全保障”；并且，在2019 年10 月26 日、2021 年6 月10 日和2021 年8 月20 日，《中华人民共和国密码法》《中华人民共和国数据安全法》和《中华人民共和国个人信息保护法》相继问世，这对口令认证技术提出了更高的要求。

面对即将产业化的量子计算机、不断更新的口令攻击手段，以及国家对网络和信息系统的高安全需求，本文对目前格上PAKE 协议的研究现状进行分析与总结，以期为相关领域研究人员提供更清晰的现状梳理和为未来研究方向提供借鉴。

1 预备知识

本节主要介绍后续综述所需的基本概念、格上困难问题、公钥加密体制、平滑投影哈希函数（SPHF,smooth projective hash function）和PAKE协议的安全性分析模型等。首先给出必要的符号说明，其中，矩阵和向量分别用加粗的大写和小写字母表示，如矩阵A和向量a；其他参数含义如表1 所示。

表1 参数含义

1.1 基本概念

定义1格[41]。设矩阵A ∈Rm×n，且A的列向量线性无关。格Λ可定义为

其中，A为格Λ的基矩阵，m为格Λ的维数，n为格Λ的秩。

定义2理想格[42]。设k为正整数，n=2k，多项式f(x)=x n+1 ∈Z[x]，另设多项式环为R=Z[x] ＜f(x)＞，环R中的元素为＜g(x)＞=，且g(x)的系数是 Zn中的元素。令I是环R的理想，则I中所有元素的系数构成 Zn的一个子格，称对应于理想I(I⊆R=Z[x] ＜f(x)＞) 的一个子格（关于Zn的子格）为f-理想格。

定义3离散高斯分布[43]。设高斯函数的中心为c，平滑参数为β（β∈ (0,1)）。另设随机向量x和高斯权重函数的表达式为

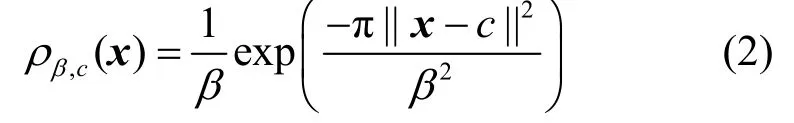
对于格Λ∈Zm，令

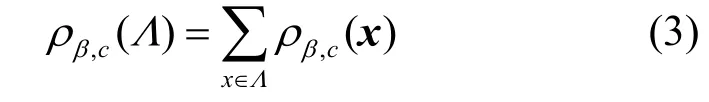
进一步，定义格Λ上的离散高斯分布为

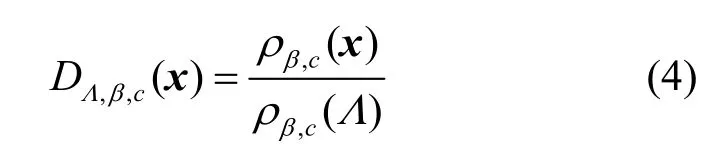
特别地，若c=0，可将DΛ,β,c简记为DΛ,β。

下文中的错误概率分布采用截断离散高斯分布[37]，即DΛ,β的定义域为||x||＜βn。根据Katz 等[37]研究，在统计上，截断高斯分布与非截断高斯分布相近，因此下文直接称截断高斯分布为高斯分布。本文用表示Zq上的某分布，取样方法为y←DΛ,β，输出「qy」(modq)[37]。

1.2 公钥加密体制

公钥加密是指由对应的唯一一对密钥（包括公钥和私钥）组成的加密算法。根据安全性的不同，公钥加密方案可分为选择明文攻击下不可区分性（IND-CPA,indistinguishability under chosen-plaintext attack）安全和选择密文攻击下不可区分性（IND-CCA,indistinguishability under chosen-ciphertext attack）安全2 种；进一步，根据攻击者或敌手能力的不同，IND-CCA 安全又可以分为IND-CCA1 安全（在现有文献中，有时直接称IND-CCA1 安全为IND-CCA 安全）和适应性选择密文攻击下不可区分（IND-CCA2,indistinguishability under adaptive chosen-ciphertext attack）安全。下面，正式给出3 种安全性的定义。

定义7IND-CPA 安全。设κ为安全参数，对于给定的公钥加密方案PKE=(KeyGen,Enc,Dec)，令任意概率多项式时间（PPT,probabilistic polynomial time）敌手A执行以下游戏（也称为实验）。

1) 系统建立：模拟器运行密钥生成算法生成公私钥对(pk,sk) ←KeyGen(1κ)，并向PPT 敌手A公开公钥pk。

2) 询问阶段：A向模拟器（也可以是挑战预言机）进行多项式有界次的加密询问。

3) 挑战阶段：A选择2 个等长的不同明文m1,m2，并向模拟器发送 (m1,m2)；模拟器选择随机比特b←r{0,1}，计算挑战密文c*←Enc(m*,pk)，并向A发送c*。

4) 猜测阶段：A收到挑战密文c*后，输出关于b的猜测比特b'。

若b'=b，则称敌手成功，并定义此时的敌手优势为

若对于任意PPT 敌手A，存在可忽略函数negl(κ)，使此时的敌手优势满足(κ) ≤negl(κ)，则称公钥加密 方 案PKE=(KeyGen,Enc,Dec)是IND-CPA 安全的。

定义8IND-CCA2 安全。设κ为安全参数，对于给定的公钥加密方案PKE=(KeyGen,Enc,Dec)，令任意PPT 敌手A执行以下游戏。

1) 系统建立：模拟器运行密钥生成算法生成公私钥对(pk,sk) ←KeyGen(1κ)，并向PPT 敌手A公开公钥pk。

2) 询问阶段1：A向模拟器进行多项式有界次的加/解密询问。

3) 挑战阶段：A选择2 个等长的不同明文m1,m2，并向模拟器发送 (m1,m2)；模拟器选择随机比特，计算挑战密文c*←Enc(m*,pk)，并向A发送c*。

4) 询问阶段2：A收到挑战密文c*后，向模拟器进行多项式有界次的加/解密询问。

5) 猜测阶段：A输出b的猜测比特b' 。

若b'=b，则称敌手成功，并定义此时的敌手优势为

该游戏与定义8 中游戏的不同之处在于，其不能执行“询问阶段2”，即敌手A收到模拟器发送的挑战密文c*后，不能再向模拟器进行加/解密询问。

1.3 平滑投影哈希函数

平滑投影哈希函数是一种隐式证明方法，其概念最初由Cramer 等[47]提出，Katz 等[33]根据格上的应用需求对此概念进行修改，本文采用Katz 等[33]的相关定义。平滑投影哈希函数是构造唯口令PAKE 协议的有效数学工具，除此之外，还可应用于零知识证明、不经意传输和证据加密等领域。

设口令为pw，pw 的集合为D，并设公钥加密方案的公钥为pk；令Cpk表示与pk 对应的 (label,C)对的集合，其中，label 表示有效标签，C表示与pk相对应的密文。对于给定的pk，定义集合X和{Lpw}pw∈D如下[32]：1)X:={(label,C,pw) | (label,C)∈Cpk&&pw∈D}；2)Lpw:={(label,Enc(pk,pw ||label),pw∈D)}。

X表示三元组 (label,C,pw) 的集合，本文称三元组 (label,C,pw) 为一个单词，用W表示。单词 (label,C,pw) 的第一个元素为有效标签label，第三个元素为口令pw∈D，第二个元素为与pw 相对应的合法密文。令L={Lpw| pw∈D}，易知L⊂X。

下面，正式给出SPHF 的定义。

定义10 平滑投影哈希函数[37]。首先给出近似SPHF 的概念。设汉明距离函数为Ham，错误比例参数为ε；哈希密钥为kh，哈希密钥的长度为l，kh的集合为KH；投影密钥为kp,kp 的集合为KP；Hash 表示哈希函数，其定义域为X、值域为Zq；由Hash 构成的哈希函数簇用ℋ 表示；ProjKG 表示定义域为KH、值域为KP 的投影函数。近似SPHF可由取样算法定义，输入公钥pk 和集合L、X，输出 (K,G,ℋ={Hash(W,kh):X→ {0,1}n},S,ProjKG(kh): KH → KP)，且满足以下条件。

2) 近似正确性：对于 ∀W=（label,C,pw）∈L，哈希值有2 种计算方式，其一为通过哈希密钥计算h=Hash（W,kh）；其二为由投影密钥kp 计算，即存在投影哈希函数ProjHash，满足以投影密钥kp、单词W和W∈L的证据r为输入，以投影哈希值ph为输出，且哈希值h与投影哈希值ph 近似相等，即式(7)成立。

特别地，若错误比例参数ε=0，则上述近似平滑投影哈希函数为平滑投影哈希函数。此外，上述投影密钥的计算不依赖密文，所以上述SPHF 是非适应性SPHF[48]。

近似SPHF 只能实现近似正确性，Benhamouda等[48]给出了通过纠错码算法实现正确性放大从而得到SPHF 的通用技术，现介绍该技术。

令{HashKG',ProjKG',Hash',ProjHash'}为近似SPHF，值域为{0,1}v；令ECC 为纠错码算法，可以纠正ε比例的错误，那么下述{HashKG,ProjKG,Hash,ProjHash}是SPHF。

kh ←HashKG(params)：输入 kh1←hashKG'(params)，在ECC 的定义域中随机选择kh2，输出哈希密钥 kh :=(kh1,kh2)。

鉴于存在标准技术能够将近似平滑投影哈希函数转换为平滑投影哈希函数，为方便描述，下文中直接省略“近似”二字。

1.4 PAKE 协议安全性分析模型

早期协议，也包括PAKE 协议的安全性分析是启发式的，这使协议的研究陷入了“设计→攻击→改进→攻击→改进”的循环，因此可证明安全逐渐成为安全协议设计的必要目标。协议的安全性分析模型一般定义了协议的通信环境（包括敌手模型）和安全性等，是研究可证明安全方案的重要基础，下面介绍PAKE 协议的安全性分析模型。

Bellare 等[49]提出的安全性分析模型一般称为BR 模型，是第一个针对实例认证和密钥交换的标准安全性分析模型，该模型面向的是对称两方协议。Bellare 等[50]基于BR 模型提出了一种针对三方协议的安全性分析模型。Blake-Wilson 等[51]进一步提出了一种针对非对称协议的安全性分析模型。Mackenzie[52]和Bellare 等[26]提出了面向口令认证的安全性分析模型，其中Bellare 等[26]提出的安全性分析模型是目前应用最广泛的PAKE 协议安全性分析模型之一，一般称为BPR 模型，下面介绍该模型。

假设PAKE 协议在公开网络上展开，参与方包括合法用户u∈ User、合法服务器s∈Sever 和非法敌手 A ∈ Adervasry={A,ℬ,ℳ,…}。假设敌手可以执行仿冒、篡改、重放、窃听、中间人等攻击[53]。另设口令空间为D，其大小为||D||。

在BPR 模型中，敌手与合法参与方（包括用户和服务器）之间通过以下预言机进行交互，实际上是敌手与各实例的交互。

下面，给出BPR 模型中伙伴关系、正确性、新鲜性、敌手优势和安全的PAKE 协议等定义。

定义13 新鲜性[26]。设用户u与服务器s是伙伴关系，如果敌手未访问过Reveal(u,i)预言机，且未访问过Reveal(s,j) 预言机，则称实例是新鲜的实例。

设用户u与服务器s是伙伴关系，并设PPT 敌手执行Test(u,i) 预言机询问后给出了猜测比特b'。若敌手未访问过Reveal(u,i) 和Reveal(s,j) 预言机，且b'=b，称敌手攻击成功。

定义14 敌手优势[26]。设A表示攻击协议Π的PPT 敌手，且A可对一个实例执行多项式次Execute、Send、Reveal 预言机询问，但能且只能对新鲜的实例执行一次Test 预言机询问。用Success表示“敌手攻击成功”事件，定义A攻击协议Π的优势AdvA,Π为

设κ是安全参数，negl(κ)是关于κ的可忽略函数。理想情况下，鉴于b的随机性，敌手攻击成功的概率为根据式(9)，此时敌手优势为AdvA,Π=negl(κ)，那么敌手A在统计上不能区分真实的会话密钥和与之等长的随机字符串。因此，会话密钥是安全的，这表示PAKE协议具备语义安全性。

人脑的记忆能力有限，用户倾向于选择短的、低熵的口令，且用户经常在多个网站使用相同或相近的口令，因而用户实际使用的口令空间较小。鉴于此，敌手总可以通过穷尽口令空间的方式来执行在线仿冒攻击，这导致PAKE 协议无法避免在线口令猜测攻击[54]。一般情况下，若此类攻击是敌手的最佳攻击方式，则称PAKE 协议是安全的。

定义15 安全的PAKE 协议。设κ是安全参数，A是攻击协议Π的PPT 敌手，且A执行在线口令猜测攻击的次数上限为Q(κ)。假设口令服从均匀分布，并用D表示口令空间，||D|| 表示口令空间的大小，则称协议Π是安全的口令认证密钥交换协议，如果对于所有的PPT 敌手A，存在可忽略函数negl(κ)满足

2 基于格的两方PAKE 协议

现阶段，在基于格的PAKE 协议领域中，有关两方PAKE 协议的成果最为丰富。两方PAKE 协议的典型应用场景如图1 所示，参与方包括一个用户和一个认证服务器，其中用户持有口令pw，认证服务器通常存储口令或口令的哈希值、与口令相关的令牌等。根据认证服务器是否直接存储口令，格上的两方PAKE 协议大致可以分为对称和非对称两类。

2.1 对称两方PAKE 协议

对称PAKE 协议在服务器端直接存储了用户口令，用于对用户进行认证。在格上实现对称PAKE协议的技术路线一般为基于格上的公钥加密算法，通过设计基于格的SPHF 实现格上的两方PAKE 协议。该技术路线的技术难点在于构建基于格的SPHF，这是因为LWE 问题只具备不完全加法同态性，直接基于格上困难问题设计的SPHF 难以满足正确性要求。为此，Katz 等[37]提出了近似SPHF 的概念，并首次给出了在格上实现PAKE 协议的可行方法，该方法也成为构造格上PAKE 协议的典型方法，即利用基于格的近似SPHF 和纠错码技术来实现（精确）SPHF 的功能，进而实现基于格的PAKE协议。Katz 等[37]由此提出了第一个基于格的SPHF和PAKE 协议。该协议属于KOY/GL 架构[10-11]，因而是基于标准安全模型的，且该协议需要3 轮通信，在用户和服务器端都需要基于IND-CCA2安全的公钥加密算法。

JG/GK 架构[12-13]是另一种基于标准安全模型的典型PAKE 架构，Ding 等[55]基于此架构提出了一种基于格的高效PAKE 协议。与Katz 等[37]的方案相比，该协议虽然也需要3 轮通信，但实现了互认证，且该协议在用户端只需要使用IND-CPA 安全的公钥加密算法，因而提高了用户端的性能。Ding 等[55]曾断言，除非基于格的精确SPHF 更加高效，否则没有必要设计格上的精确SPHF。但在2013 年，Blazy等[56]提出了一种基于LWE问题的精确SPHF，并指出精确SPHF 至少可以使PAKE 协议的构造不局限于BPR 安全模型。

借鉴基于传统困难问题的PAKE 协议的研究路线，减少通信轮（次）和弱化协议所基于的安全性假设依然是格上PAKE 协议的重要优化方向。Zhang等[57]首先提出了一种基于格的可拆分公钥加密算法，并基于此提出了一种基于格的非适应性SPHF，这2 种构造除用于实现PAKE 协议外，还具有相对独立的研究价值；然后，基于Abdalla 等[58]的通用两轮PAKE 协议架构，Zhang 等[57]提出了一种格上的两轮两方PAKE 协议。

Zhang 等[57]提出的两轮PAKE 架构需要使用模拟健全的非交互式零知识（SS-NIZK,simulation sound non-interactive zero-knowledge）证明，因此执行效率较低，且目前格上还不存在标准模型下的SS-NIZK 证明，所以Zhang 等[57]的方案需要使用随机预言机。为此，同样基于Abdalla 等[58]提出的通用两轮PAKE 协议架构，Benhamouda 等[48]提出了格上第一个不需要使用SS-NIZK 证明的两轮PAKE 协议。在此基础上，Li 等[44]利用MP 公钥加密方案[59]，也提出了一种格上不需要SS-NIZK 证明的两轮PAKE 协议。该协议通过弱化协议所基于的安全性假设（在服务器端只需要基于IND-CPA 的安全模型）降低了协议各方面的开销。尹安琪等[60]通过安全性证明指出，Li 等[44]将两轮PAKE 协议中服务器端的安全性假设降低到IND-CPA 不能保证协议的安全性；进一步，尹安琪等[60]提出了一种格上可证明安全的两轮PAKE 协议，该协议将用户端的安全性假设降低到IND-CPA，因而降低了用户端的计算、通信和存储等开销。2018 年，基于Katz 等[33]提出的通用一轮PAKE 架构，Benhamouda 等[48]利用其所提出的格上非适应性SPHF 和SS-NIZK 证明，给出了一种格上一轮PAKE 协议的实现方法，但没有给出具体的协议构造和安全性证明。Li 等[61]基于Benhamouda 等[48]的研究，利用MP 公钥加密方案[59]，提出了一种高效的基于格的SPHF，并基于此实现了一种格上的一轮PAKE 协议。

为进一步提高格上PAKE 协议的执行效率和降低协议各方面的开销，格上PAKE 协议的另一个研究方向是基于理想格上困难问题（如RLWE 困难问题）来构造协议。2010 年，Lyubashevsky 等[62]提出了LWE 问题在环上的变体——RLWE 问题，并将RLWE 问题的困难性规约到理想格上困难问题中最难实例的求解。基于RLWE 问题的加密体制很好地克服了基于欧氏格的密码体制（如LWE 问题）中密钥过长的缺陷，并且可以通过快速傅里叶变换算法提高加/解密运算速度。2013 年，叶茂等[63]提出了一种基于理想格的SPHF，该SPHF 可用于构造基于理想格的PAKE 协议，从而提高协议性能。2019 年，利用Lyubashevsky 等[62]基于RLWE 问题的公钥加密方案，Karbasi 等[64]提出了一种基于理想格的SPHF，并基于此在KOY/GL 架构[10,65]下构造了一种基于理想格的PAKE 协议。

表2 对比了不同对称PAKE 协议的性能对比。通信轮（次）特指服务器与用户之间的通信轮（次），其中，通信轮数是指通信双方之间双向通信的数量，次数是指通信双方之间单向通信的数量；如果是异步通信，通信轮数等于通信次数，如果是同步通信，通信次数是通信轮数的2 倍。

根据表2，格上PAKE 协议的通信轮次由Katz等[37]、Ding 等[55]方案的3 轮架构，逐渐发展到Zhang等[57]的两轮架构和Benhamouda 等[48]和Li 等[61]的一轮架构，从而得到了具有最优通信轮次的PAKE协议。更少的通信轮（次）通常代表更低的通信开销和更低的通信风险，一直是格上PAKE 协议的重要优化方向。但低轮（次）的PAKE 协议一般无法实现显式认证，只能实现隐式认证。

表2 不同对称PAKE 协议的性能对比

目前，格上的部分低轮（次）PAKE 协议（包括Zhang 等[57]的两轮方案和Benhamouda 等[48]、Li等[61]一轮PAKE 方案等）需要使用SS-NIZK 证明来保证安全性，这种昂贵的密码学原语会影响协议性能的提升，且在格上还不存在基于标准模型的SS-NIZK 证明，因此上述方案都需要使用随机预言机。随机预言机不仅在实际应用时需要被具体的哈希函数替代，还可能导致PAKE 遭受离线口令猜测攻击。此外，量子敌手可以在量子态下访问随机预言机，这进一步增大了在格密码方案中使用随机预言机的危害。因此，应该在格PAKE 方案中尽量避免随机预言机的使用。Li 等[44]和尹安琪等[60]提出的格上两轮PAKE方案同时避免了SS-NIZK证明和随机预言机的使用，相比之下安全性更高。

Katz 等[37]的3 轮PAKE 方案、Zhang 等[57]的两轮PAKE 方案，以及Benhamouda 等[48]和Li 等[61]的一轮PAKE 方案在用户端和服务器端都需要基于IND-CCA2 的安全模型。而Ding 等[55]的3 轮PAKE协议、尹安琪等[60]的两轮PAKE 协议将格上PAKE协议在用户端所基于的安全模型降低到IND-CPA安全，Li 等[44]的两轮PAKE 方案将服务器端所基于的安全模型降低到IND-CPA 安全。一般而言，基于更强安全模型的密码方案具有更大的计算和存储等开销，因此，与一轮PAKE协议相比，两轮PAKE协议虽然在通信轮（次）上存在劣势，但在用户端或服务器端可能具有更高的执行效率。

此外，与基于传统困难问题的PAKE 方案（如Katz 等[33]的方案）相比，基于格的PAKE 方案不仅可以抵抗量子攻击，且格上的基本运算是小整数的模乘/加等具有线性渐近复杂度的运算，比传统PAKE 方案的大整数模幂运算更加高效。

2.2 非对称两方PAKE 协议

对称PAKE 方案在服务器端存储了用户的口令，因此存储的或真实的口令一旦泄露，攻击者就可以轻易仿冒合法用户，即此类方案无法抵抗服务器泄露攻击。非对称PAKE 协议是解决该问题的一种有效方法，因为此类协议只需要在服务器端存储与口令相关的哈希值或验证器或者令牌，用户不需要向服务器端发送真实的口令。

目前，在格上实现非对称PAKE 方案的常用方法是基于格上困难问题实例化传统的基于传统困难问题（一般是数论困难问题）的非对称PAKE 协议。基于传统困难问题的典型非对称PAKE 方案包括SPR[7]、PAK[8]、PPK[9]方案。2017 年，Ding 等[66]利用RLWE 困难问题，分别在格上实例化了PAK和PPK 协议[8-9]，从而得到了抗量子的非对称两轮和3 轮PAKE 协议，这2 个协议在服务器端存储了口令的哈希值，Ding 等[66]还在ROM 下严格证明了这2 个协议的安全性。同年，Gao 等[67]利用RLWE困难问题在格上实例化了SPR 方案[7]，从而得到了一种抗量子的SPR 协议，并在通用可组合（UC,universally composable）模型下证明了方案的安全性；该协议只需要在服务器端存储一个与口令相关的验证器，并且该验证器不会泄露口令的任何信息。因为不需要存储口令或者口令的哈希值，该方案的安全性得到了进一步的提高。2021 年，舒琴等[68]利用Peikert 式误差调和机制，在UC 模型下提出了一种更加高效的可证明安全的非对称PAKE 协议。

Li 等[54]在2020 年指出现有的非对称PAKE 方案，更确切地说是方案中使用的口令哈希方案（PHS,password hashing scheme），要么基于ROM（使用随机预言机的局限性见本文的引言部分），要么基于传统困难问题（此类方案无法抵抗量子攻击）。为此，利用基于格的SPHF，Li 等[54]提出了第一个基于格的PHS，并在此基础上提出了一种标准模型下可证明安全的格上非对称PAKE 协议，该协议在服务器端存储了口令的哈希值，可以有效抵抗服务器泄露攻击和量子攻击。

现阶段，随着人们对个人隐私关注度的提高，很多用户期望在认证过程中隐藏个人身份信息，匿名认证方案可以有效解决该问题。2018 年，Feng等[69]基于RLWE 问题的困难性，首次提出了一种基于理想格的匿名PAKE 方案，使用户可以在不泄露身份信息的前提下，通过公开信道实现身份认证和密钥交换。Dabra 等[70]在2021 年指出Feng等[69]的方案简单、高效，但不能抵抗信号泄露攻击、电子欺骗攻击、操纵攻击和用户匿名违规攻击。基于Ding 等[71]零知识认证协议中直接公钥验证的思想，Dabra 等[70]提出了一种新的基于理想格的匿名PAKE 方案，并在ROR（real-or-random）模型下证明了方案的安全性。该方案可以抵抗信号泄露等攻击，包括注册、登录、认证和口令更新等功能。进一步，Ding 等[72]在2022 年指出，若主密钥重用，Dabra 等[70]的方案仍不能抵抗信号泄露攻击；为此，他们利用Ding 等[73]随机密钥交换方案中的思想，对Dabra 等[70]的方案进行改进，从而提出了一种改进的理想格上的匿名PAKE方案，并对方案进行了严格的安全性证明，该协议保证了方案在主密钥重用的情况下也能抵抗信号泄露攻击。

上述方案虽然可以解决服务器端的口令泄露问题，但无法解决用户端的口令泄露问题。多因子认证方式是解决该问题的有效方法，若将口令身份认证看作网络和信息系统的第一道防线，那么为解决该问题可以引入第二道防线——智能卡。2021年，基于RLWE 问题的困难性，Wang 等[74]利用Alkim 等[75]提出的格上密钥交换方案首次提出了抗量子的双因子PAKE 方案，该方案在随机预言机模型下是可证明安全的，且可以抵抗密钥重用攻击、信号泄露攻击和密钥不匹配攻击。

表3 对比了非对称PAKE 协议的性能。为对用户进行认证，Ding 等[66]、Gao 等[67]和Li 等[54]的方案在服务器端存储了口令的哈希值，而舒琴等[68]、Feng等[69]、Dabra 等[70]和Ding 等[71]的方案在服务器端存储了与口令相关的验证器。相比之下，存储口令的验证器要比存储与口令直接相关的哈希值更加安全。Li等[54]虽然也在服务器端存储了口令的哈希值，但他们提出了一种抗量子的口令哈希方案，因而提高了相应PAKE 方案的安全性。Ding 等[66]、Gao 等[67]、Feng等[69]方案的安全性是基于随机预言机的，本文在引言部分总结了使用随机预言机的潜在安全威胁。Dabra等[70]、Ding 等[71]方案的安全性是基于ROR 模型[76]的，Li等[54]的非对称PAKE方案是基于标准模型的，这两类方案都避免了随机预言机的使用，因而具有更高的实际安全性。舒琴等[68]的方案在UC 模型下仍然是可证明安全的，在表3 所有的协议中具有更强的实际安全性。

表3 非对称PAKE 协议的性能对比

Feng 等[69]、Dabra 等[70]和Ding 等[72]的匿名非对称PAKE 方案使用户可以在不公开个人身份信息的前提下进行身份认证和密钥交换，因而保护了用户的个人隐私。Feng 等[69]的方案不能抵抗信号泄露攻击，Dabra 等[70]的方案在主密钥重用的情况下也不能抵抗此类攻击，而Ding 等[72]的方案在主密钥重用的情况下依然可以抵抗此类攻击。

3 基于格的三方PAKE 协议

现有格上PAKE 协议的研究多针对两方应用场景，即多为两方PAKE 协议，此类方案要求每2 个用户之间都共享一个口令或口令的哈希值等，因而此类方案在应用于大规模通信系统时会产生繁重的口令管理问题。另一方面，由于人脑的记忆能力有限，用户可记忆口令的数目和长度有限，一般只能记忆5～7 个短的、低熵的口令[77]；若用户重复使用口令，将带来严重的安全问题。三方PAKE 协议可以有效解决该问题，其典型应用场景如图2 所示。协议参与方包括多个用户和一个认证服务器，每个用户只需要与可信服务器共享一个口令，就可以实现与任意其他用户（同样与可信服务器共享口令的用户）进行身份认证与密钥交换。

图2 三方PAKE 协议的典型应用场景

虽然存在通用的技术可以基于两方PAKE 协议实现三方PAKE 协议[76]，但会增加协议的通信轮（次），并且无法实现显式认证。因此，2013 年，叶茂等[78]在JG/GK[12-13]架构的基础上，首次提出了基于格的三方PAKE 协议，并在标准模型下证明了协议的安全性。在该协议中，每个用户与认证服务器都可以在3 轮通信内实现显式的互认证。2017 年，Xu 等[79]基于RLWE 问题，在随机预言机模型下提出了一种格上的三方PAKE 协议，并严格证明了协议的安全性；与叶茂等[78]的方案相比，该方案的通信轮（次）更多，但由于环上的运算可以通过快速傅里叶变换加速，因此该协议具有较小的计算开销。2018 年，于金霞等[80]利用Zhang 等[57]提出的两方PAKE 协议，提出了一种基于格的两轮三方PAKE 协议，但未克服Zhang 等[57]的方案仅能实现密钥传输的问题，因而用户所得到的会话密钥仅由服务器端确定。2020 年，Yin 等[81]提出了一种新的可证明安全的格上两轮三方PAKE协议，与于金霞等[80]的方案相比，该方案中的会话密钥由认证双方同时确定，提高了密钥协商的公平性。

表4 对比了不同三方PAKE 协议的性能。与Abdalla 等[76]的传统三方PAKE 协议相比，叶茂等[78]、于金霞等[80]、Xu 等[79]、Yin 等[81]的三方PAKE 协议基于格上困难问题，因而可以抵抗量子攻击。此外，Abdalla 等[74]的方案使用了大整数模/幂运算，与格上的小整数向量/矩阵运算相比，开销较大。Xu 等[79]的三方PAKE 协议不仅需要用户与可信服务器进行通信，还需要用户之间进行通信。相比之下，叶茂等[78]、于金霞等[80]和Yin 等[81]的三方PAKE 协议只需要用户与服务器进行通信就能实现身份认证与密钥交换。Xu 等[79]方案的优势是基于RLWE 困难问题，因而计算开销较小。

表4 不同三方PAKE 协议的性能对比

叶茂等[78]的格上三方PAKE 协议需要3 轮通信，而于金霞等[80]和Yin等[81]的方案需要两轮通信，减小了协议的通信轮（次）。叶茂等[78]的三方PAKE协议的通信数据类型包括密文、投影密钥和消息认证码，该方案的密文复杂度、投影密钥大于尹安琪等[80]的三方3PAKE 协议。Yin 等[81]、于金霞等[80]的三方PAKE 协议采用了可拆分公钥加密体制，只需要验证密文有效性就可以实现IND-CCA2 安全，避免了消息认证码的传输。Xu 等[79]、于金霞等[80]、Yin 等[81]的格上三方PAKE 协议需要使用随机预言机，但叶茂等[78]的方案是基于标准模型的，因而安全性更高。

4 基于格的分布式PAKE 协议

第2 节和第3 节中的PAKE 协议都属于集中式认证方案，用户认证信息（口令、口令的哈希值或与口令相关的令牌）都存储在单个服务器上。若服务器端直接存储了口令，则PAKE 协议将面临服务器泄露攻击的威胁；若在服务器端简单存储了口令的哈希值，则协议仍面临离线字典攻击的威胁。虽然在服务器端存储口令相关的验证器可以有效抵抗上述攻击，但相关研究成果较少。而敌手执行此类攻击的收益率很大，因为只需入侵存在安全漏洞的单个服务器，就有可能获取数以千万计的口令数据。例如在2021 年，仅RockYou2021 数据集就泄露了约84 亿条口令记录。分布式认证为解决服务器端的口令泄露问题提供了另一种解决方案。

图3 给出了分布式PAKE 协议的典型应用场景。在一次协议执行中，参与方包括一个用户和多个认证服务器，其中用户持有口令，多个认证服务器分布式地存储口令份额，对用户的认证由多个认证服务器协同完成。敌手入侵部分服务器（一般是小于相应阈值数目的服务器）不会泄露口令的任何信息。目前，格上的相关研究成果较少。2021 年，Roy 等[82]通过基于格的秘密共享算法提出了格上首个分布式PAKE 协议，该协议可以抵抗量子攻击和服务器攻击，但需要基于PKI 模型，因而用户在进行认证时除了需要记忆口令外，还需要存储和管理系统公钥。Roy 等[82]的方案是一种阈值方案，不适用于服务器数目小于阈值的应用场景，如两服务器场景。2022 年，尹安琪等[83]通过设计基于格的两方SPHF，提出了格上第一个两服务器PAKE 协议，并在标准模型下证明了该协议的安全性。该协议实现了唯口令设置，因而可部署性更强。目前，格上分布式PAKE 协议的相关研究成果较少，对比之下，基于传统困难问题的分布式PAKE 方案的研究成果相对丰富，大致可分为以下3 类：基于PKI 模型的方案[84-85]、基于身份的方案[86-87]和唯口令的方案[88]。在这3 类方案中，除用户口令外，前两类分别需要用户管理系统公钥和服务器身份等信息。

图3 分布式PAKE 协议的典型应用场景

表5 给出了不同分布式PAKE 协议的性能对比。Katz 等[89]、Yi 等[86]、Yi 等[87]和Raimondo 等[88]的协议基于DDH 困难问题，无法抵抗量子攻击；Roy等[82]和尹安琪等[83]的分布式PAKE 协议基于格上的困难问题，可以抵抗量子攻击。

Roy 等[82]的方案基于PKI 模型，用户在进行身份认证时除了需要记忆口令外，还需要存储服务器公钥；Yi 等[86]、Yi 等[87]的方案是基于身份的，用户需要额外管理服务器身份信息；Katz 等[89]、Raimondo 等[88]和尹安琪等[83]的方案实现了唯口令设置，因而其所对应的安全系统具有更强的可部署性。Katz 等[89]、Yi 等[86]、Yi 等[87]和尹安琪等[83]的分布式PAKE 方案是两服务器认证方案，适合两服务器应用场景；Roy 等[82]、Raimondo 等[88]的分布式PAKE 协议是阈值方案，适合服务器数目大于相应阈值的应用场景。

在用户和服务器之间，Katz 等[89]、Yi 等[87]、Roy等[82]和Raimondo 等[88]的方案需要3 轮通信，Yi 等[86]的方案需要两轮通信，尹安琪等[83]的协议则需要一轮通信，通信轮（次）不断得到优化。多服务器PAKE方案[82,88]与两服务器PAKE 方案[83,86-87,89]相比一般需要更多的通信次数。在表5 的协议中，除尹安琪等[83]的协议外，其他协议[82,86-89]都需要使用签名/验签算法。Raimondo 等[88]、Katz 等[89]和尹安琪等[83]（被动敌手攻击下的协议）避免了零知识证明的使用，有助于协议性能的提升；此外，Roy 等[82]的方案在每次协议执行时都需要多次使用秘密共享算法，这会进一步增加协议各方案的开销。

在Roy 等[82]的协议中，会话密钥由一方确定，相比之下，表5 中其他方案[83,86-88]的会话密钥由认证双方同时确定，这使密钥协商更加公平。Yi 等[86]、Yi 等[87]的协议是否需要使用随机预言机取决于其所基于的密码学原语，而Katz 等[89]、Raimondo 等[88]、Roy 等[82]和尹安琪等[83]的协议基于标准模型，所以直接避免了随机预言机的使用。

表5 不同分布式PAKE 协议的性能对比

5 未来研究方向

根据以上分析可知，现阶段格上PAKE 协议的研究已经取得了一定的成果。但由于起步较晚且投入相对不足，现有格上PAKE 协议的相关技术还存在诸多局限性，也面临许多挑战，在未来的研究工作中，可以更多地关注以下几个方面。

1) 量子随机预言机模型（QROM,quantum random oracle model）中可证明安全的PAKE 方案。基于ROM 的方案与基于标准模型的方案相比，一般在执行效率上具有显著优势。目前，基于ROM的格PAKE 方案在证明安全性时一般只考虑具有经典访问权限的敌手，但相关方案被实例化后，随机预言机也被具体的哈希函数替代，此时量子敌手可以对随机预言机进行量子访问——QROM。因此，在经典ROM 下，可证明安全的方案可能无法抵抗量子敌手的攻击。而在QROM 下证明方案的安全性比在经典模型下更加困难：一是量子敌手可以在输入的指数叠加上查询随机预言机，因而在QROM下高效地模拟随机预言机是困难的；二是经典的ROM 证明技术对QROM 来说并不适用。因此，为保证格PAKE 方案的高效性和安全性，需要研究在QROM 中可证明安全的相关方案。

2) 基于格的分布式口令更新方案。在基于口令的相关方案中，口令更新是一个基本的且重要的问题。但据本文所知，目前还不存在基于格的分布式口令更新方案。Raimondo 等[88]提出了基于传统困难问题的门限口令更新方案，但无法抵抗量子攻击。虽然存在基于格的成熟技术可以解决单服务器设置下的口令更新问题[69]，但利用此类方案无法直接构造分布式口令更新方案：一是在两服务器或多服务器设置下，存在2 个或多个服务器身份（在单服务器设置下，只有一个服务器身份）；二是此时服务器并不存储用户口令的哈希值。因此，设计实现基于格的分布式口令更新方案，从而使基于口令的分布式身份认证系统的功能更加完善，是一个有挑战且有重要现实意义的研究方向。

3) 基于格的口令哈希方案。口令哈希方案是构造非对称PAKE 方案的重要数学组件。口令哈希方案可以对口令进行哈希处理，并将其与用户名等其他重要信息一起存储在服务器上，以便在用户端登录时服务器可以验证用户端注册的口令[54]。当前的口令哈希函数要么基于经典ROM，因而不具备QROM 下的可证明安全性；要么基于传统困难问题，无法抵抗量子攻击。据本文所知，目前格上只存在一种标准模型下的口令哈希方案[54]，该方案在计算效率上还存在优化空间。若要使格上PAKE 方案更加安全实用，一是可以在QROM 下构造高效的（或在标准模型下构造更加有效的）格上口令哈希方案，二是要使方案能够满足口令隐藏性、保熵性、预哈希保熵性，且能抵抗原像攻击、二次原像攻击等。鉴于工业领域中非对称PAKE 协议应用的广泛性，基于格的口令哈希方案是一个具有重要现实意义的研究方向。

6 结束语

基于格的PAKE 协议可以抵抗量子攻击，不存在高熵密钥的管理问题，也不涉及用户不可撤销的隐私泄露问题，因而所对应的安全系统具有较强的可部署性。口令认证是应用最广泛的身份认证技术之一，而基于格的PAKE 协议在后量子时代也将具有重要的意义。本文对现有的基于格的PAKE 协议进行了研究综述，主要介绍了基于格的两方PAKE协议（包括对称和非对称PAKE 协议）、三方PAKE协议和分布式PAKE 协议，并分别对比了不同类型PAKE 方案的安全性、通信轮（次）、认证方式等，最后展望了基于格的PAKE 协议的未来研究方向。