基于Udwadia−Kalaba 理论的自行车机器人平衡控制方法

张佳乐，赵睿英✉，冯艳丽，杨皓，武琳琳

1) 长安大学工程机械学院公路养护装备国家工程研究中心，西安 710064 2) 西北工业大学航天学院，西安 710068

自行车是一种使用历史悠久的代步交通工具，具有结构简单、环保、经济、用途广泛等优点，其历史可大约追溯到第二次工业革命时期[1].进入21 世纪，随着计算和传感技术的飞速发展，使得自动驾驶成为一个热门而重要的研究课题.自行车的广阔市场为无人驾驶自行车创造了巨大的机会[2].无人驾驶自行车机器人具有运动灵活、车身狭小等特点，从而能够广泛应用到灾区救援、娱乐表演、物流运输等场景中[3]，因此得到了众多学者对该类型自行车的研究与关注.

近年来，围绕着自行车机器人的稳定平衡控制策略问题，国内外的学者开展了深入的研究.其中，Tanaka 和Murakami[4]通过控制转向角或利用离心力来控制平衡.然而，该方法无法实现自行车静止状态的平衡控制.Lee 和Ham[5]则是通过改变质心的位置来控制机器人的平衡，但该方法增加了自行车的重量，导致系统的响应时间较慢.Schwab 和Meijaard[6]，以及Vu 和Nguyen[7]则指出通过转向车把来平衡低速（静止）状态的自行车困难较大，在这种情况下，可采用角动量轮进行侧向平衡控制，相比之下，该方法可以实现在静止状态下的车体平衡控制.目前，已有一些使用角动量轮进行机器人自平衡的线性控制方法被提出.其中，Lam[8]和Lee等[9]对自行车的横滚角度进行实时测量，采用PD 控制算法与PID 控制算法，实现了两自由度自行车机器人的平衡控制.Chen等[10]将自行车动态模型进行线性化和离散化，设计了模型预测控制器来实现自行车的平衡控制，使用了两个旋转方向相反的飞轮来抵消自行车偏航动力学中的反作用力矩，对于每个飞轮，需要两个执行器来调节围绕两个正交轴的角速度，但会使平衡设备的复杂性增加.Sprya 和Girard[11]对动力学模型进行了线性化处理，并采用极点置零法设计了平衡控制器.上述方法大多需要对模型进行线性化处理，但自行车机器人是一个复杂的非线性系统，模型简化会降低控制系统精度.针对这些问题，Cui等[12]提出了一种基于互联和阻尼分配的无源控制方法（IDA-PBC）的非线性控制器，为简化辅助平衡设备仅使用一个飞轮，将与飞轮旋转方向相反的扭矩用于自行车的平衡控制.Zhang等[13]设计了一种非线性控制器，通过控制陀螺仪进行自行车的平衡控制.此外，也有许多其他两轮自行车的非线性平衡控制方法被提出，Beznos等[14]的非线性控制以及Chen 和Dao[15]的模糊控制方法等，这些控制方法考虑了自行车机器人系统的非线性因素，利用反馈信息设计机器人平衡控制器，有效解决了模型简化所产生的控制系统精度受限的问题，成为了自行车机器人控制领域的研究热点.

与上述传统的非线性控制方法不同，张新荣等[16]，Udwadia 和Kalaba[17]以及Chen[18]基于Udwadia−Kalaba（U−K）理论从一个新的角度出发，将控制目标视为受控对象的伺服约束条件，并通过产生主动伺服约束力使受控系统实现控制目标，即利用主动控制的思想来解决机械系统的控制问题.该方法是专门针对机械系统的一种新非线性控制方法，并被应用至不同领域中，其中：赵韩等[19]在机械臂位置控制方面应用了该方法，能够较好地解决伺服约束控制方面问题.Zhao等[20]考虑了系统的关节摩擦以及不确定性的影响，将该方法应用到非线性Delta 并联机器人的鲁棒控制中，并验证了系统稳定性与有效性.Chen等[21]针对欠驱动移动机器人的平衡控制问题，提出了一种基于U−K 理论的自适应律的控制方法，该自适应律可根据系统存在的不确定性不断进行跟踪误差的调整.韩江等[22]将一种基于U−K 理论的轨迹跟踪控制方法应用到六轴协作机器人上，使系统具有较好的稳定性.Yin等[23]在解决车辆横向和偏航运动控制问题中使用了该方法，通过数值仿真结果验证了该方法的有效性.此外，董方方和赵晓敏[24]将该方法应用到柔性机器人控制中，通过理论分析与仿真结果，验证了该控制方法可以完成系统的轨迹跟踪控制任务.然而该方法在自行车机器人领域的应用尚未涉及，论文利用该方法对自行车机器人侧向平衡控制进行研究，具有一定的理论意义和应用价值.

综上所述，本文基于U-K 理论，针对自行车机器人侧向自平衡问题，提出了一种满足系统平衡要求的主动控制方法.相比于传统的反馈控制方法，该方法从一个新的角度来解决自行车机器人的平衡控制问题，克服了初始偏差的干扰，实现了不同初始横滚角速度下自行车机器人的侧向平衡约束跟随控制，并借助MATLAB 软件对该控制方法进行了数值仿真，验证了该系统的稳定性和有效性，可实现自行车机器人系统的侧向自平衡控制.

1 Udwadia−Kalaba 方程

Udwadia−Kalaba 方程是一类用于描述受约束系统动力学问题的方程.考虑一个机械系统包含n个质点，整个系统在任意时刻t的位形可由广义坐标向量q∈Rn表示，系统的广义速度向量为∈Rn，广义加速度向量为∈Rn.无约束条件下，机械系统的运动方程可以表述为：

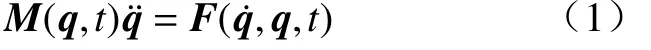
其中：t为时间；M(q,t)=MT(q,t)∈Rn×n为质量矩阵（或惯性矩阵）；F(,q,t)∈Rn包括重力、外力和离心力/科式力[25].

如果该机械系统受到一组约束（完整约束或非完整约束），约束方程为：

则，

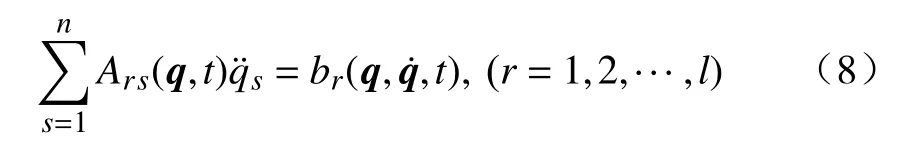
将上式用矩阵形式表示为：

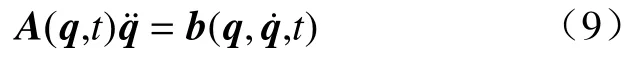
其中，b(·)=[b1b2···bl]T.假定机械系统处于理想情况下，则做出以下假设：

假设1：对于任意(q,t)∈Rn×R，系统惯性矩阵M−1(q,t)>0.

假设2：对于所有q,t)∈Rn×R，rank[A(q,t)]≥1.

假设3：约束方程是相容的，对于任意A(q,t)和b(,q,t)，至少存在一个满足约束方程.

定理1：满足假设1 至假设3，受约束的机械系统运动方程，即Udwadia−Kalaba 方程[17]：

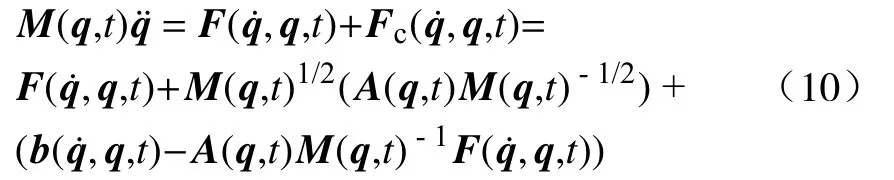
其中，Fc(,q,t)为约束力，(A(q,t)M(q,t)−1/2)+为A(q,t)M(q,t)−1/2的逆矩阵[26].

当系统受到一个伺服约束，且不存在初始偏差和不确定性时，控制器可以基于模型设计为τ=Fc(,q,t)，可使系统满足约束方程（9），实现控制要求.对于欠驱动系统，其独立的控制输入变量个数少于系统的自由度个数，因此，常用于全驱动机器人的控制方法通常难以直接应用到自行车机器人控制系统中，则控制器可以基于模型架构成B(q,t)τ形式，来实现系统的控制要求.其中B(q,t)∈Rn×u为系统的输入矩阵，τ ∈Ru×1为系统的控制扭矩，且n>u[24].

2 自行车机器人动力学建模和控制

2.1 机器人动力学模型

自行车机器人结构简图如图1 所示.O−XYZ代表全局惯性参考坐标系，其中O为后轮与地面接触点，OX是机器人行走方向，OZ是垂直地面向上的方向，θ为横滚角（机器人相对于垂直面的倾斜角度），θ1为角动量轮旋转角度，整个机器人的质心用点P表示，m1和m2分别表示机器人（包括前后轮）和角动量轮的质量，L1和L2分别表示从地面到机器人质心和角动量轮质心的距离，除角动量轮外的机器人绕X轴的转动惯量为I1，角动量轮的转动惯量为I2，g表示重力加速度.

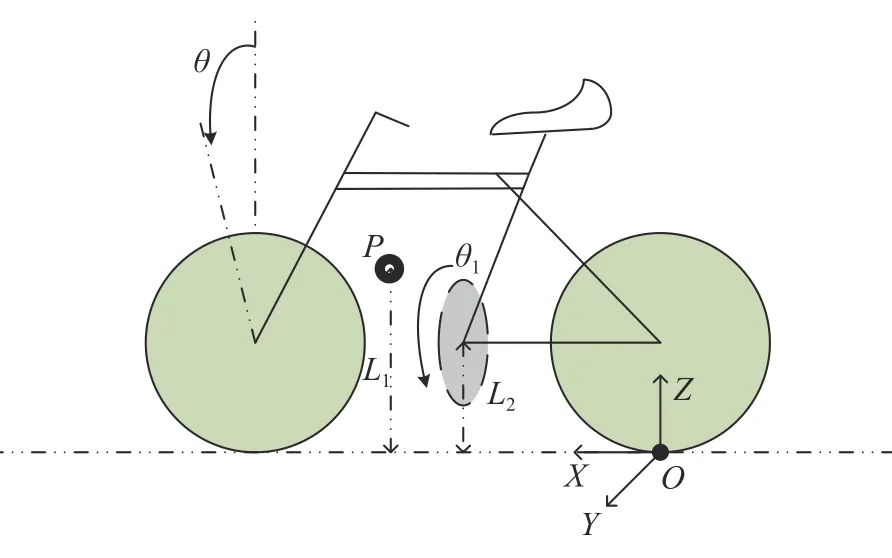
图1 自行车机器人结构简图Fig.1 Simplified structure diagram of bicycle robot

利用欧拉-拉格朗日方程建立机器人的无约束动力学模型[27]：

其中：W为拉格朗日量；T为系统动能；U为系统势能；Qi为系统所受外力;q=[θ,θ1]T.系统的运动可分为两部分：平动和转动.对于平动运动，自行车机器人质心和角动量轮质心的速度分别为:

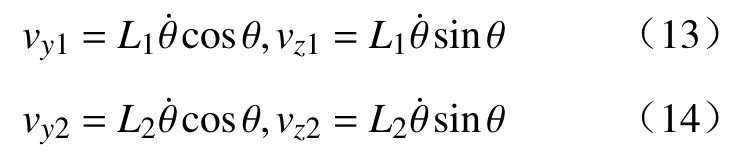
其中：vy1为自行车机器人Y方向的线速度；vz1为自行车机器人Z方向的线速度；vy2为角动量轮Y方向的线速度；vz2为角动量轮Z方向的线速度.

机器人和角动量轮的转动速度（ω1和ω2）为：

因此结合式（13）～（15），系统的动能可表示为：

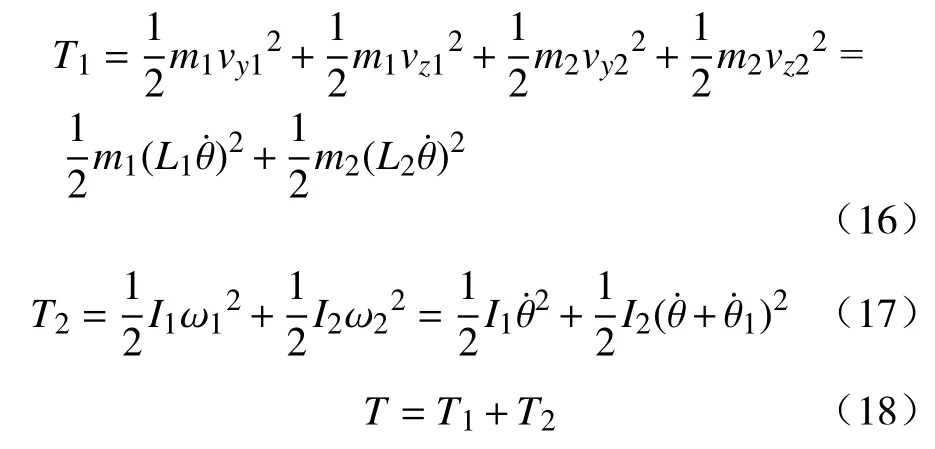
其中：T1为系统平动动能；T2为系统转动动能.

系统的势能表示为：

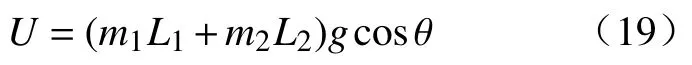
结合式（12），自行车机器人系统静止时刻的动力学方程可表示为：

其中，B=[0;1]为系统的输入矩阵；τ ∈R1×1为角动量轮提供的控制扭矩.

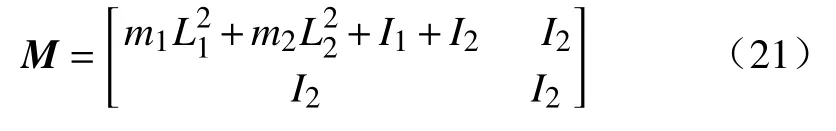
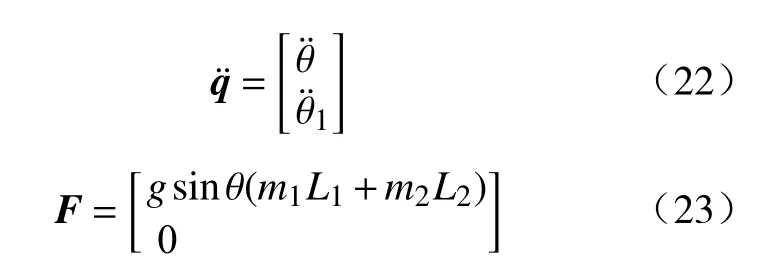
2.2 控制器设计

当自行车机器人存在一定的初始横滚角速度[t,∞)→Rn，且qt连续，则机器人系统的期望速度，期望加速度.而后将系统的位置误差为零看作系统的一个完整约束，即q−qt=0.定义系统位置误差：

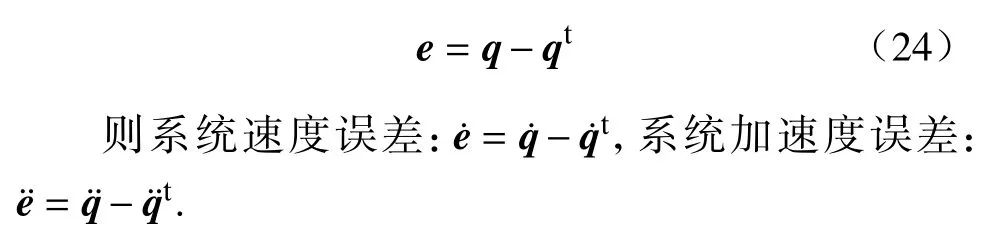
为使系统位置能够完全到达期望位置，需要满足以下约束：

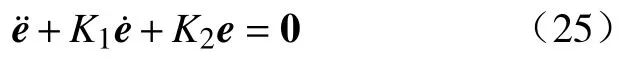
其中，K1与K2为常数，且K1，K2均大于0.

将式（25）重新表达为矩阵形式：

其中：A1=[1 0]；b1=−K2θ；qt(θ=0).

根据定理1 可以得出维持机器人侧向平衡的约束力模型，且该模型是实现平衡约束所需扭矩的最小值[28]，根据约束力的解析模型，设计系统的控制扭矩 τ[29]为：

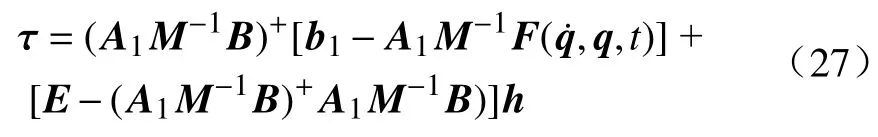
其中：h∈Rn为任意向量；E为单位矩阵.

该控制器设计可以消除初始位置误差的影响，令自行车机器人横滚角 θ快速收敛到平衡位置，使系统达到稳定状态.其控制器设计步骤总结为：首先根据侧向平衡条件，构造出自行车机器人平衡控制的运动学约束；然后将该约束重新表达为二阶矩阵形式；最后根据定理1，设计出满足式(26)平衡约束条件的控制扭矩 τ.其流程如图2所示.

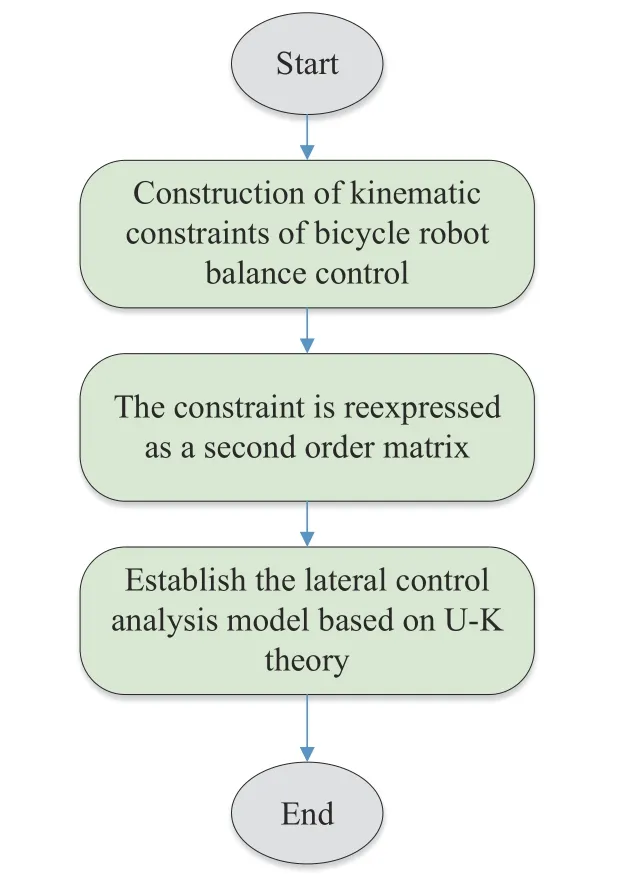
图2 自平衡控制器设计流程图Fig.2 Flow chart of controller design

3 仿真及结果分析

假设自行车机器人仿真参数如表1 所示[30]，利用MATLAB ODE45 对自行车机器人进行数值仿真.初始值设定如下：q=[10 0]，=[1 0]，仿真结果如图3～图5 所示.

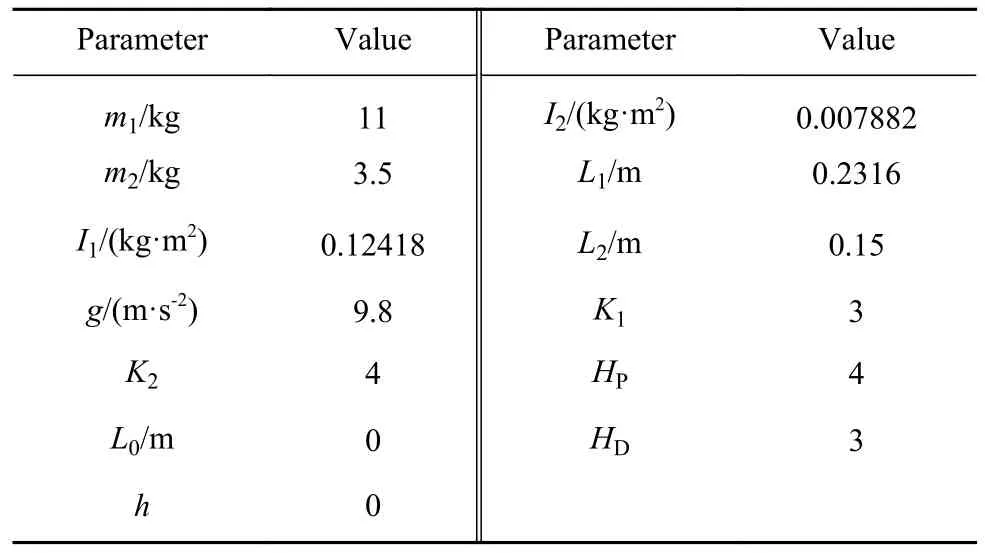
表1 自行车机器人参数表Table 1 Bicycle robot parameters

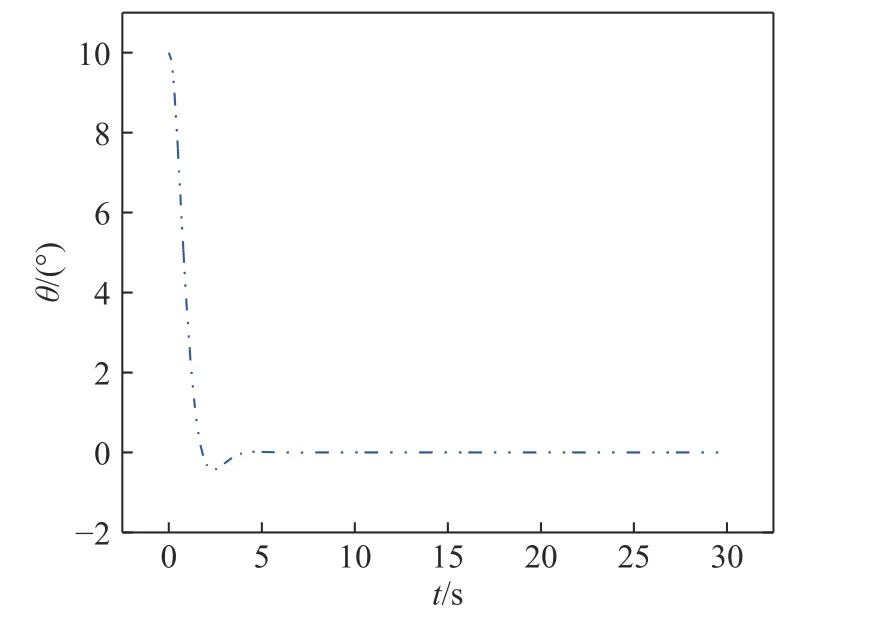
图3 横滚角曲线图Fig.3 Angle graph

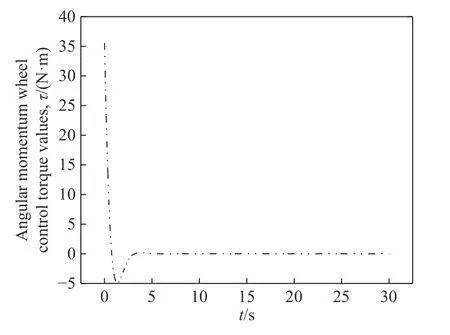
图4 扭矩曲线图Fig.4 Torque graph

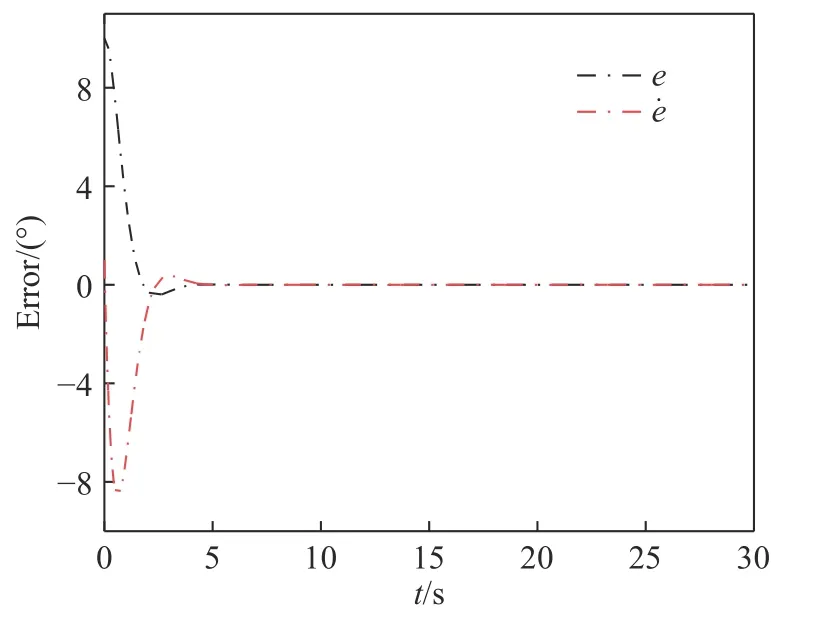
图5 误差曲线图Fig.5 Error graph

图3 与图4 分别表示自行车机器人横滚角 θ与角动量轮提供的控制扭矩值 τ随时间t变化的曲线图.当初始横滚角 θ为10°时，在角动量轮所提供控制扭矩的作用下，系统的横滚角 θ约5 s 后收敛于平衡位置.

图5 所示为系统的位置误差值e与速度误差值随时间t变化的曲线图.图6 呈现了角动量轮提供的控制扭矩值τ、时间t与位置误差值e的关系图，随着时间t的增大或位置误差值e的减小，控制扭矩值 τ逐渐减小.

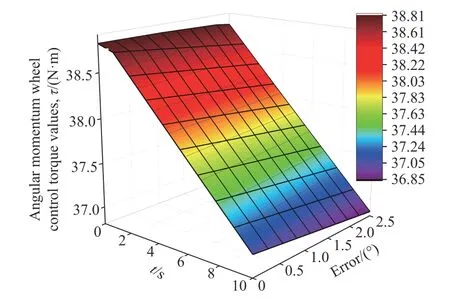
图6 扭矩角度误差曲线图Fig.6 Torque and angle error graph

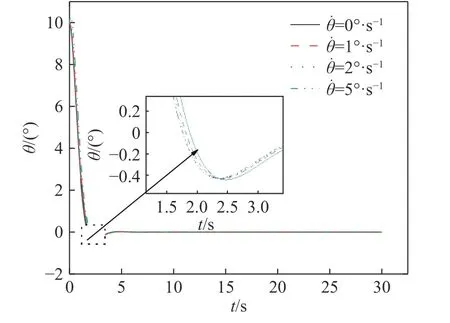
图7 横滚角度曲线图Fig.7 Angle curves

图7 所示为自行车机器人横滚角 θ在不同的初始横滚角速度 θ˙的情况下随时间t变化的曲线图，可知横滚角 θ由初始给定的10°开始衰减，在2.4 s左右减至−0.4°，约5 s 后稳定收敛于期望值0°.图8所示为自行车机器人横滚角速度在不同的初始横滚角速度的情况下随时间t变化的曲线图，可知横滚角速度随着初始偏差干扰的增大，其超调量的绝对值逐渐增大.图9 所示为角动量轮的旋转角速度在不同的初始横滚角速度的情况下随时间t变化的曲线图.图10 所示为角动量轮提供的控制扭矩值 τ在不同的初始横滚角速度的情况下随时间t变化的曲线图，从局部放大图可知，仿真伊始随着初始横滚角速度 θ˙的增大，所需控制扭矩值 τ随之增大.

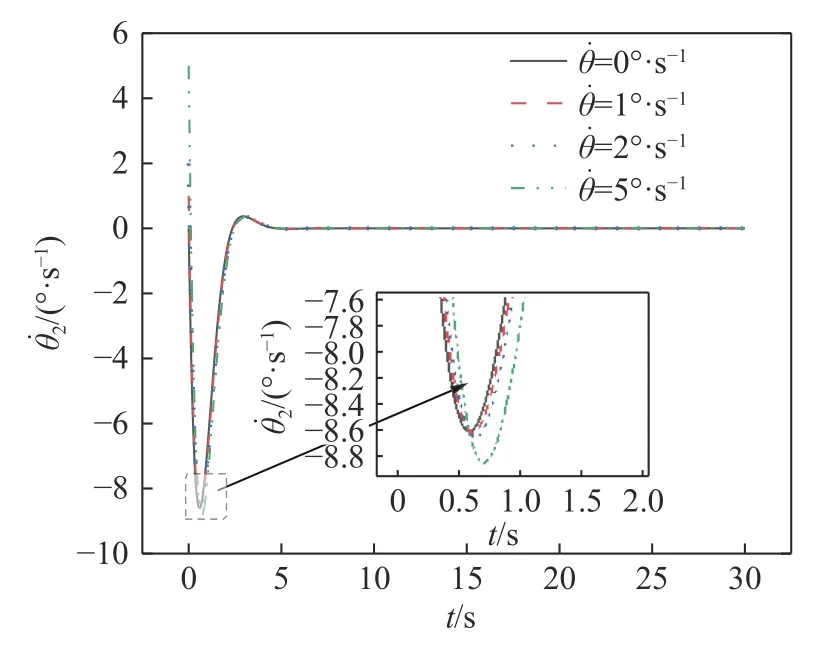
图8 横滚角速度曲线图Fig.8 Angular velocity curves

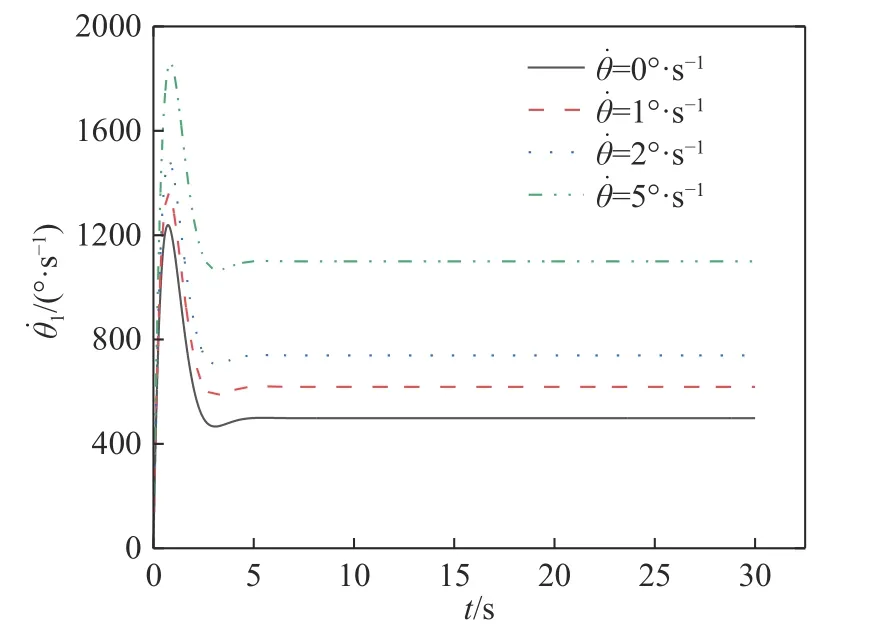
图9 角动量轮角速度曲线图Fig.9 Angular momentum wheel angular velocity curves

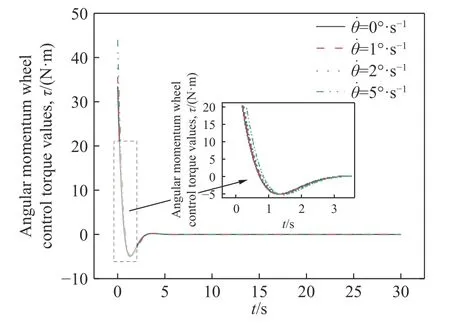
图10 扭矩曲线图Fig.10 Torque graph

为了与本文提出的约束跟随控制器进行控比较，我们提出了以下针对自行车机器人自平衡系统的传统PD 控制器[31]：

其中：τ′为PD 控制器产生的控制扭矩；HD为微分系数；HP为比例系数.

图11 为PD 控制器simulink 环境下的系统框架图，图12 为传统PD 控制器与本文约束跟随控制器仿真对比曲线图，从仿真结果可知本文采用的控制方法较于传统的PD 控制方法，具有系统响应速度快、超调量小以及系统震荡次数显著减少等特点.

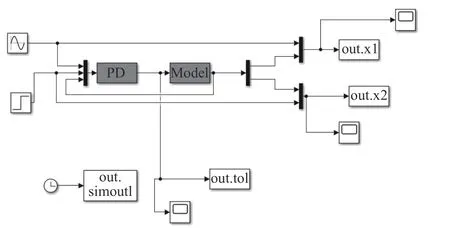
图11 PD 控制器simulink 框架图Fig.11 Simiulink frame diagram of PD controller

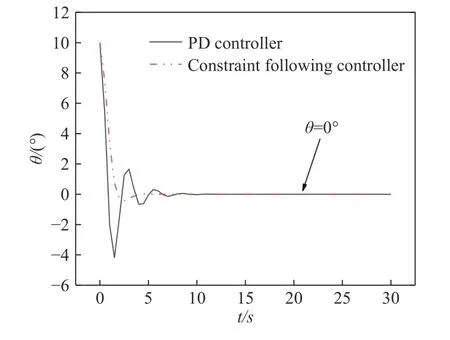
图12 PD 控制器和约束跟随控制器对比曲线图Fig.12 Comparison of PD controller and constraint following controller

4 结论

(1) 本文将Udwadia−Kalaba 理论应用至装有角动量轮的自行车机器人静止状态平衡控制中，阐述了该方法的原理与应用条件，并依据侧向平衡条件，构造出机器人平衡控制的运动学约束，建立了满足运动约束的扭矩解析模型，该解析模型可以实现所需平衡控制的最小扭矩.

(2) 通过仿真分析的方式，说明了所设计的约束跟随控制器可在不同初始横滚角速度下，实现自行车机器人系统的自平衡控制，保证了该控制系统的稳定性和有效性.相比于传统的PD 反馈控制方法，该方法具有系统响应时间快、超调量小等优点.因此，该方法可为无人驾驶自行车机器人的侧向平衡问题提供一种新的控制方法.