低温条件下边坡岩石动态力学特性实验研究

高峰，杨根，熊信，周科平，李聪，李杰林

1) 中南大学资源与安全工程学院，长沙 410083 2) 中南大学高海拔寒区采矿工程技术研究中心，长沙 410083

我国多年冻结区和季节性冻结区面积广泛，在这些地区进行工程建设和矿产资源开采必须考虑特殊的地质和气候条件.以西藏昌都江达县玉龙铜矿为例，矿区海拔4569～5118 m，最冷月日平均最低气温约−20 ℃，冻结期长达7 个多月，边坡稳定性受冻融作用显著，冻结岩层给爆破开挖带来诸多困难，制约了矿山生产效率.国内外针对寒区岩石、岩体的冻融问题进行了大量研究，并取得了一定成果[1−9]，其研究内容以冻融过程中岩石内部的细观结构变化、冻融前后岩石常温动静态力学性质差异、寒区边坡失稳为主，对低温条件下的岩石力学性质研究较少，而研究冻结岩石的动态力学性质对高寒地区开挖爆破工程和边坡稳定性分析更具实际意义.

针对冻结条件下的岩石力学性质，Yamabe 和Neaupane[10]进行了砂岩在不同温度下的单轴、三轴实验，得到拉压强度、弹性模量随温度的变化规律.Park等[11]对−160～ 40 ℃温度范围内岩石的热膨胀系数、变形规律进行了室内实验，为评价低温条件下地下设施的稳定性提供了一定依据.赵涛等[12]研究了低温下岩石拉压强度随温度的变化规律，认为不同冻结温度下孔隙冰和未冻水的含量不同,导致不同温度下岩石抗压强度和抗拉强度差异巨大.刘波等[13]研究了不同初始含水率冻结砂岩的强度特性，提出了不考虑冻胀损伤的强度强化机制和考虑冻胀损伤的强度强化机制.同时，不同学者根据力学实验结果，得出了冻结条件下岩石的三轴蠕变模型[14−15]或强度预测模型[16]，为寒区岩体稳定性提出一定思考.

而在针对冻结岩石的动态力学研究中，单仁亮等[17]针对西北地区采用冻结钻爆法进行掘进时井壁的安全性问题，按照相似比理论展开模型试验研究，研究了钻爆法的安全性.杨阳等[18]研究了低温冻结红砂岩的温度效应和应变率效应，发现低温水冰相变对冻结砂岩的劣化作用，并研究了低温下的冲击分形特征及破坏模式.王建国等[19]研究了饱水冻结花岗岩的应变率效应和能耗特征.总结冻结岩石的动态力学研究成果发现，缺乏冻结岩样动力学性质与常温岩样的比较，对造成冻岩动态力学特异性原因分析较少.因此，为了研究不同应变率下不同状态岩样动态压缩力学性质，对寒区边坡大理岩在干燥、饱水和冻结条件下进行了一系列动态压缩试验，并分析了冻岩动态力学特异性原因，研究结论对寒区工程建设和矿山采掘有一定的参考意义.

1 试验设备和流程

1.1 试验装置

实验中采用的SHPB 试验系统的入射杆、透射杆及异形冲头材料相同，均为40Cr 合金钢，合金钢纵波波速为5400 m∙s−1，弹性模量240 GPa，密度为7810 kg∙m−3.对于低温冻结冲击实验，考虑到室温对实验的影响，对SHPB 实验装置加以改造，以控制冲击实验的环境温度，减弱室温改变对岩石动力学特性的影响.图1 是所设计低温环境箱、SHPB 压杆系统和相关设备的示意图.低温环境箱建在SHPB 平台上，环境箱主体结构为有机玻璃，粘结后气密性良好，玻璃内外壁紧贴绝热材料.箱侧底部、上端有连接进装置内部的不锈钢导管，导管设置开关阀以控制低温氮气进出.箱的两个侧面开有直径稍大于50 mm 的圆孔，以方便入射杆、透射杆在同一方向上来回移动，圆孔周围附有气密材料，以确保环境箱内外隔绝.环境箱正面设有活页门，以方便放入、取出试样.箱内部设有热电偶以监测实验过程中的温度变化，温度精度为0.1 ℃.

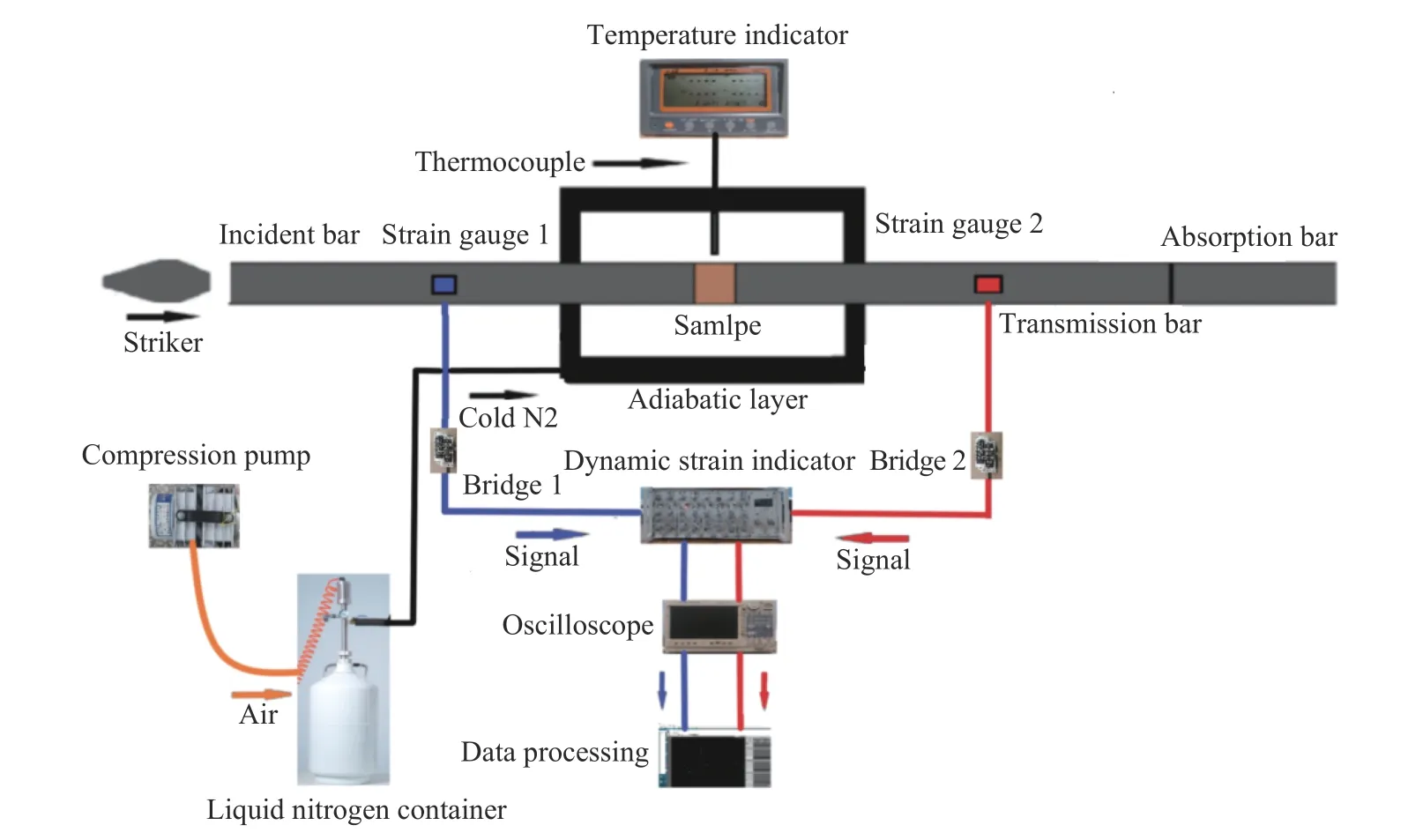
图1 含低温控制系统的SHPB 实验系统图Fig.1 Diagram of the SHPB experimental system with a cryogenic control system

进行低温冻结力学试验时，先打开低温氮气阀，环境箱内温度迅速下降，通过氮气阀控制进气速率，待箱内温度稳定在−20 ℃后，将冻结岩石从岩石冻结箱内取出，用绝热手套夹持在箱内入射杆、透射杆之间，立刻进行试验.

1.2 试样制备

岩石试样由西藏玉龙铜矿露天边坡钻孔岩芯制备而来，试件的动态力学实验在直径50 mm 霍普金森压杆（SHPB）试验装置上完成，根据SHPB实验对试件尺寸要求，将岩芯切割、打磨、抛光制成ϕ50 mm×50 mm 和ϕ50 mm×25 mm 的标准试样，分别用于冲击和劈裂实验.剔除表面、端面不合格岩样.严格控制直径差异，同组样品直径偏差在0.01 mm 以内.

将岩样置于干燥箱内干燥48 h后，测量岩样在干燥状态下的纵波波速和干密度，随后对岩样进行真空饱水，达到完全饱和后测得岩样的饱和密度.随后利用核磁共振系统得到岩样的核磁共振（NMR）孔隙度.得到的岩样基本物理学参数如表1 所示.

表1 岩样基本物理学参数Table 1 Basic physical parameters of rock samples

1.3 试验方案

为分析温度和含水量对岩样动态力学性质的影响，将试样分为干燥、饱水和冻结三种状态.以干燥状态作为基准，探究水软化和低温冻结时水冰相变对岩样动态力学性质的影响.干燥试样是将岩样在干燥箱内烘干至恒重，后在常温下进行实验.饱水试样是将岩样真空饱水48 h，后在常温下进行实验.冻结试样是先对岩样进行真空饱水处理，用保鲜膜包裹后放入岩石冻结箱，在−20 ℃条件下冻结48 h 后进行力学实验.由五年内江达地区的地表气温统计结果知，冻结期内，平均日最低气温为−19.8 ℃，故实验中冻结温度选择相近的−20 ℃.为确保岩样完全冻结，冻结时间设为48 h.为研究应变率大小的影响，对同状态岩石分别加0.4、0.5、0.6 和0.7 MPa 的冲击气压，且每组为3 个试件.整个实验过程如图2 所示.

2 实验原理及结果分析

2.1 应力平衡确认

实验中采用的异形冲头能产生半正弦波，由此可保证恒应变率加载.通过超动态应变仪和入射杆、透射杆上的应变片实时采集信号，达到应力平衡状态时，可计算出岩石试样的压缩峰值应力σdc、拉伸峰值应力 σdt.

图3(a)为超动态应变记录仪采集到的冲击气压为0.4 MPa 的干燥压缩试样A11 的入射波、反射波及透射波原始电信号，通过信号转换处理，可以得到A11 压缩试样两端应力随时间变化情况如图3(b)所示.由图3(b)可知，经过几次反射后透射波和入射波与反射波的叠加波基本重合，表明试样在加载过程中达到应力平衡条件.

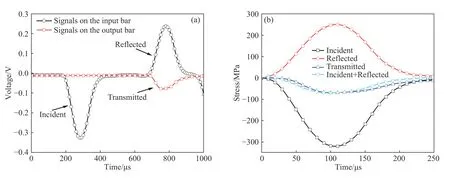
图3 应力平衡图.(a)原始信号图;(b)应力平衡图Fig.3 Stress balance diagram: (a) original signal diagram;(b) stress balance diagram

2.2 应变率、破坏时间计算

岩石的动态强度在相似的应变率下才有可比性，根据ISRM 提出的岩石材料动态抗压度确定方法，可以从应变率的时间演化来确定试样的应变率.图4 是预实验中某压缩试样应变率随时间的变化情况，由图4 可以看出，应变率的时程演化曲线存在一个近似平台区域，说明岩石在这段时间内以相对恒定速率发生变形，表明试样达到应力平衡，将这个平台内的应变率均值定义为试样的应变率[20]，应变率突增点对应的时间为试样破坏所需时间，下文中为T[21].

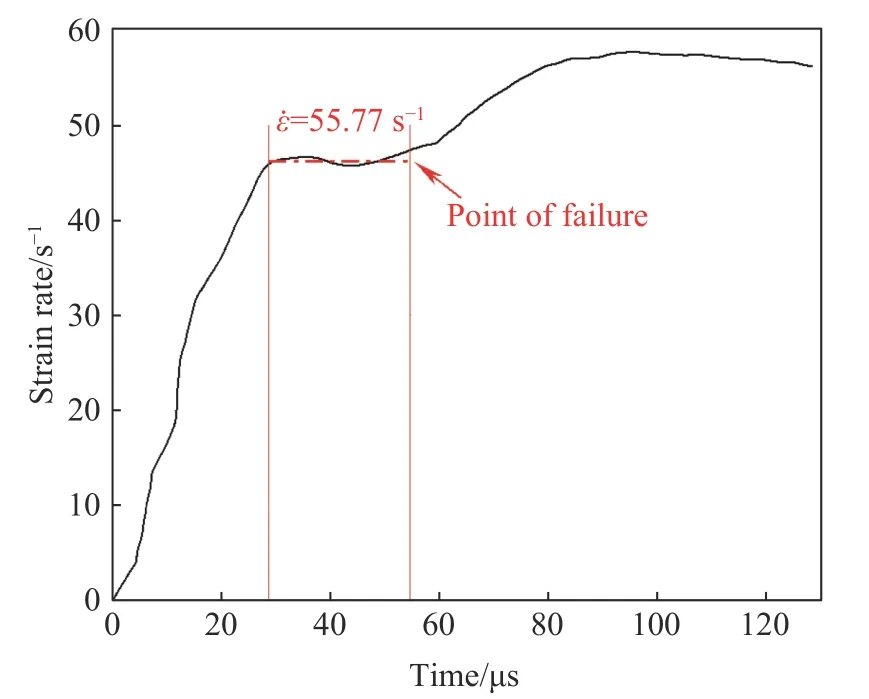
图4 试样应变率时程曲线Fig.4 Time–history curve of the strain rate of a sample

2.3 动态强度参数的应变率效应

2.3.1 应力应变曲线特征分析

图5、6、7 为不同实验条件下岩样的应力应变曲线，σ为轴向应力，ε为轴向应变.由图可以看出，受温度、含水量和岩样均质性的影响，试样的应力应变曲线形态各异，但曲线变化特征仍有一定规律：随着增大，以图5(a)为例，四条曲线应变软化阶段起始点对应横坐标分别为7.85 ×10−3,1.003×10−4,1.304×10−4和1.633×10−4，应变软化阶段起始点应变呈增大趋势，这表明岩样破坏过程中有更多裂纹参与，极限承载时的变形增大；随着增大，三种状态岩样的压缩峰值应力 σdc、拉伸峰值应力 σdt均呈增大趋势，说明常温下的应变率强化规律同样适用于低温.

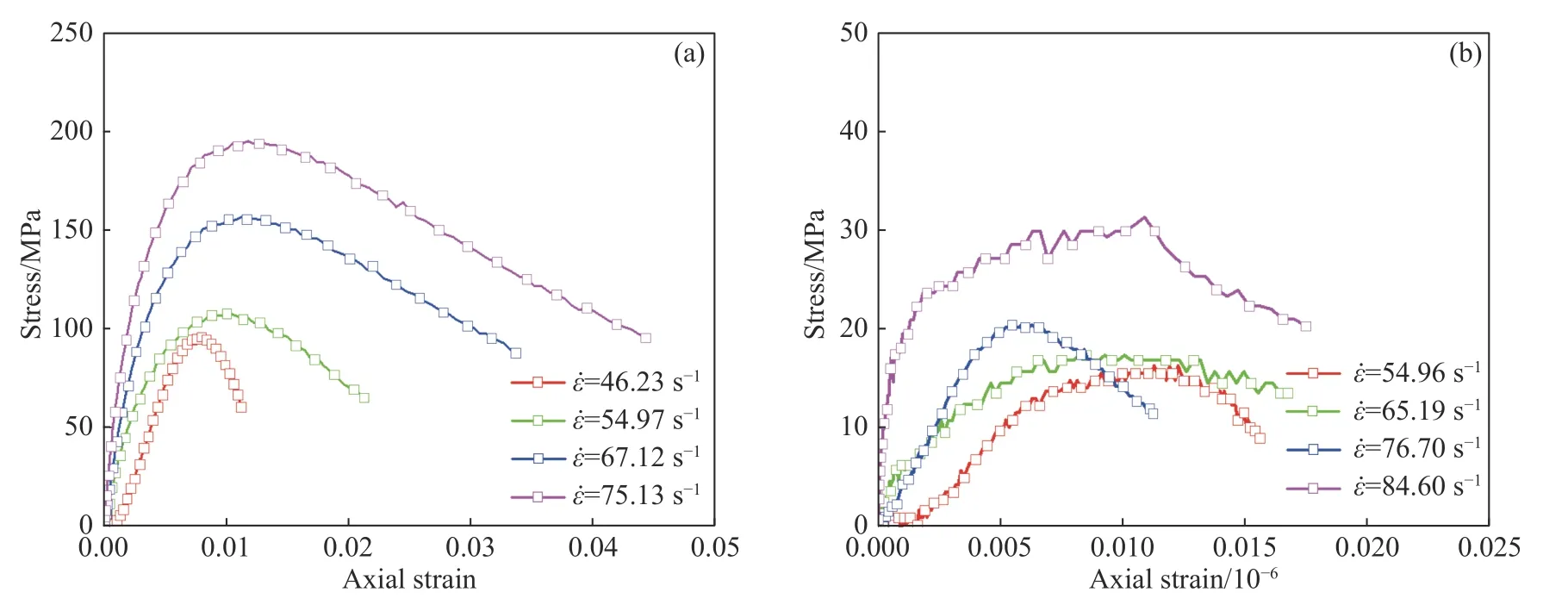
图5 不同应变率下干燥大理岩的压缩、拉伸的σ−ε曲线.(a)压缩应力应变曲线;(b)拉伸应力应变曲线Fig.5 σ−ε curves of the compression and tension of dry marble at different strain rates: (a) compressive stress–strain curves;(b) tensile stress–strain curves

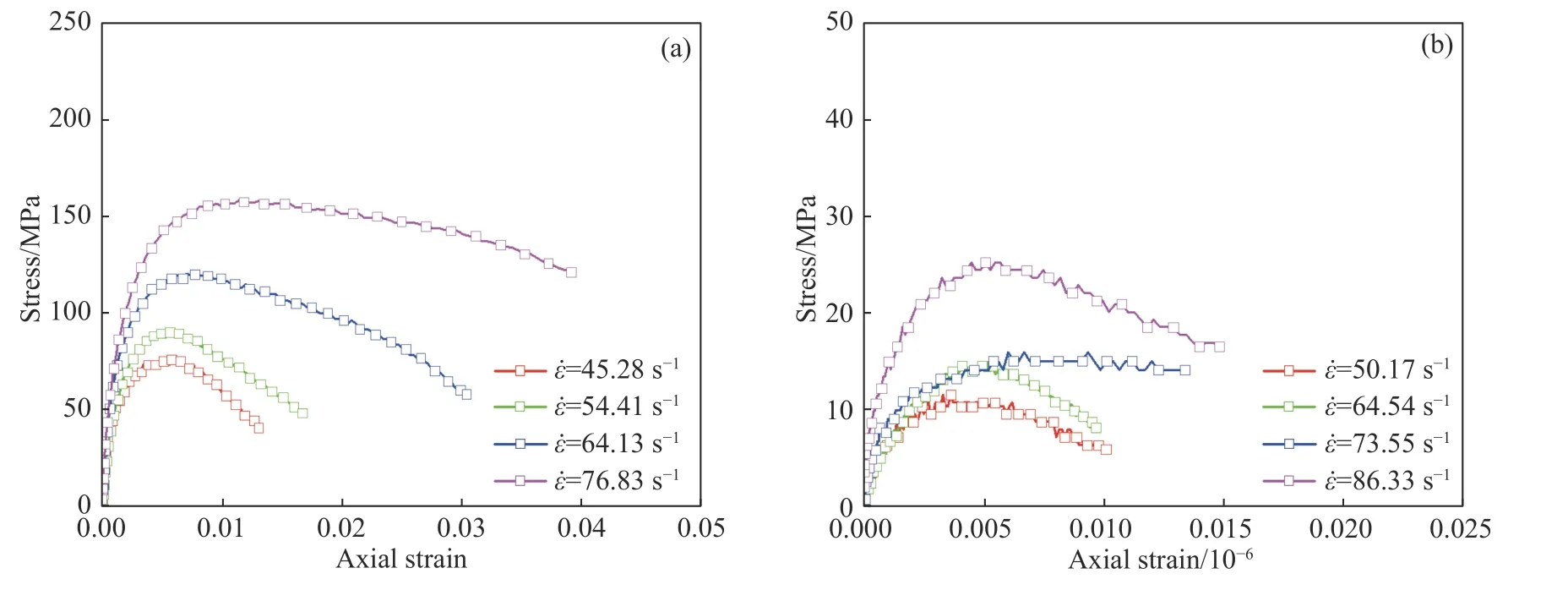
图6 不同应变率下饱水大理岩的压缩、拉伸的σ−ε曲线.(a)压缩应力应变曲线;(b)拉伸应力应变曲线Fig.6 σ−εcurves of the compression and tension of saturated marble at different strain rates: (a) compressive stress–strain curves;(b) tensile stress–strain curves

实验过程中，冻结岩样的应力应变曲线出现一定的波动现象（图7）.低温条件下空气中的水分在岩石表面发生液化现象，后因低温而冻结，同时岩样表面涂抹的耦合剂因环境温度和热交换而冻结，以上现象将导致岩样表面与入射杆、透射杆表面接触稍有不均，导致波形信号出现一定波动.在同一冲击气压下，冻结岩样的平均应变率与常温下相差很小，因此波形信号的波动对实验结果的影响在可控范围内.冻结岩样的应力应变曲线的线弹性阶段的斜率较大，初始弹性模量较大，抗变形能力强；而在塑性变形阶段，应力应变曲线出现应力平台，后经过一段应变软化过程后下降.

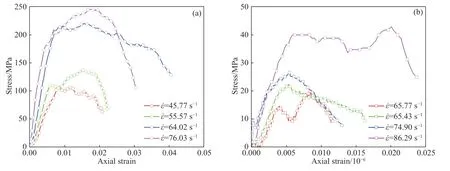
图7 不同应变率下冻结大理岩的压缩、拉伸的σ−ε曲线.(a)压缩应力应变曲线;(b)拉伸应力应变曲线Fig.7 σ−εcurves of the compression and tension of frozen marble at different strain rates: (a) compressive stress–strain curves;(b) tensile stress–strain curves

2.3.2 峰值应力随应变率变化规律

以下列函数为基础对不同状态下的峰值应力σdc、σdt进行拟合，得到各状态下大理岩峰值应力随应变率变化规律如图8、9 所示.其中，参数b反应峰值应力大小随应变率变化快慢，参数a反应峰值应力大小.

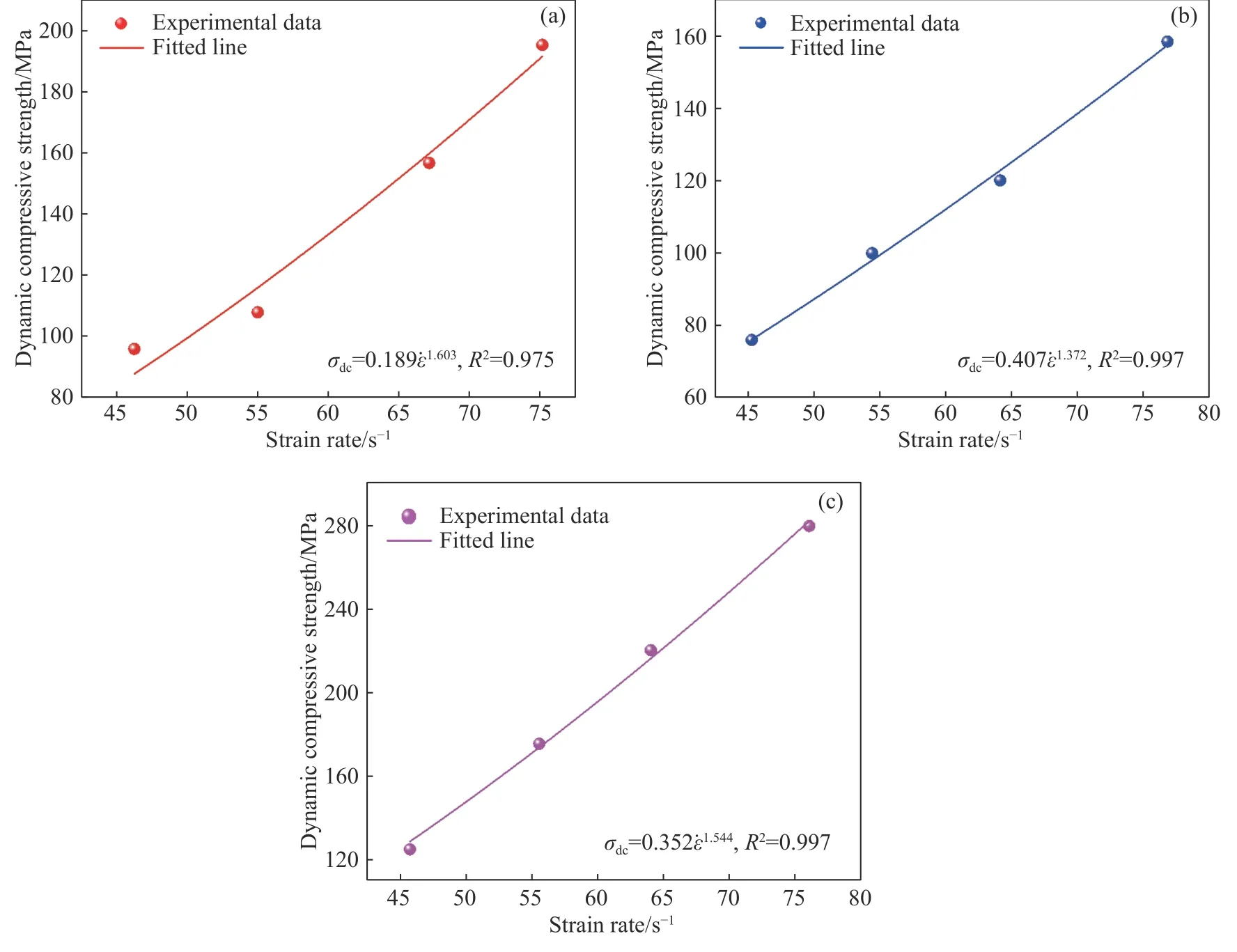
图8 不同状态岩样压缩峰值应力的应变率效应.(a)干燥;(b)饱水；(c)冻结Fig.8 Strain rate effect of the peak compressive stress of rock samples under different states: (a) drying;(b) saturated;(c) frozen

冻结条件下，岩样 σdc随应变率增加大幅增加，且大于常温时增幅，而 σdt增长幅度较常温下小.冻结条件下 σdt增幅数值大于 σdc增幅，这表明冻结岩石在应变率逐渐升高，外界扰动逐渐增强时，抗压缩能力增长缓慢，抗拉伸能力强化明显.

2.4 不同状态大理石动态性质差异

为分析比较含水量和温度对岩样动态力学特性的影响，将饱水、冻结岩石的动态强度与干燥状态作对比，定义水软化因子F1、冰强化因子F2，二者计算方式如下：

式中，σS为饱水强度，σD为干燥强度，σF为冻结强度.整理岩样峰值应力结果得到图10.根据图10，在相似应变率(相同冲击气压)下有规律 σF>σD>σS.

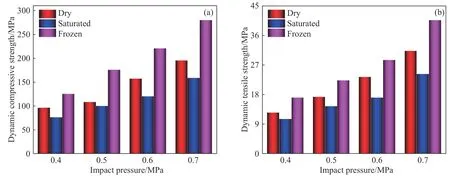
图10 不同状态岩样动态峰值应力差异.(a)压缩强度;(b)拉伸强度Fig.10 Dynamic peak stress differences of rock samples in different states: (a) compressive strength;(b) tensile strength

2.5 动力学性质差异分析

四种应变率条件下，压缩应力的水软化因子F1分别为0.79、0.93、0.76、0.81，拉伸应力的水软化因子F2分别为0.84、0.83、0.73、0.77，可知岩样中的孔隙水起到一定软化作用，且水软化作用强弱与应变率大小无明显相关性.饱水过程中，水分与岩石成分中的亲水矿物发生一系列物理化学反应，岩石内部矿物颗粒间的胶结物质遇水后受到削弱，形成水岩复合材料，宏观表现为强度降低.

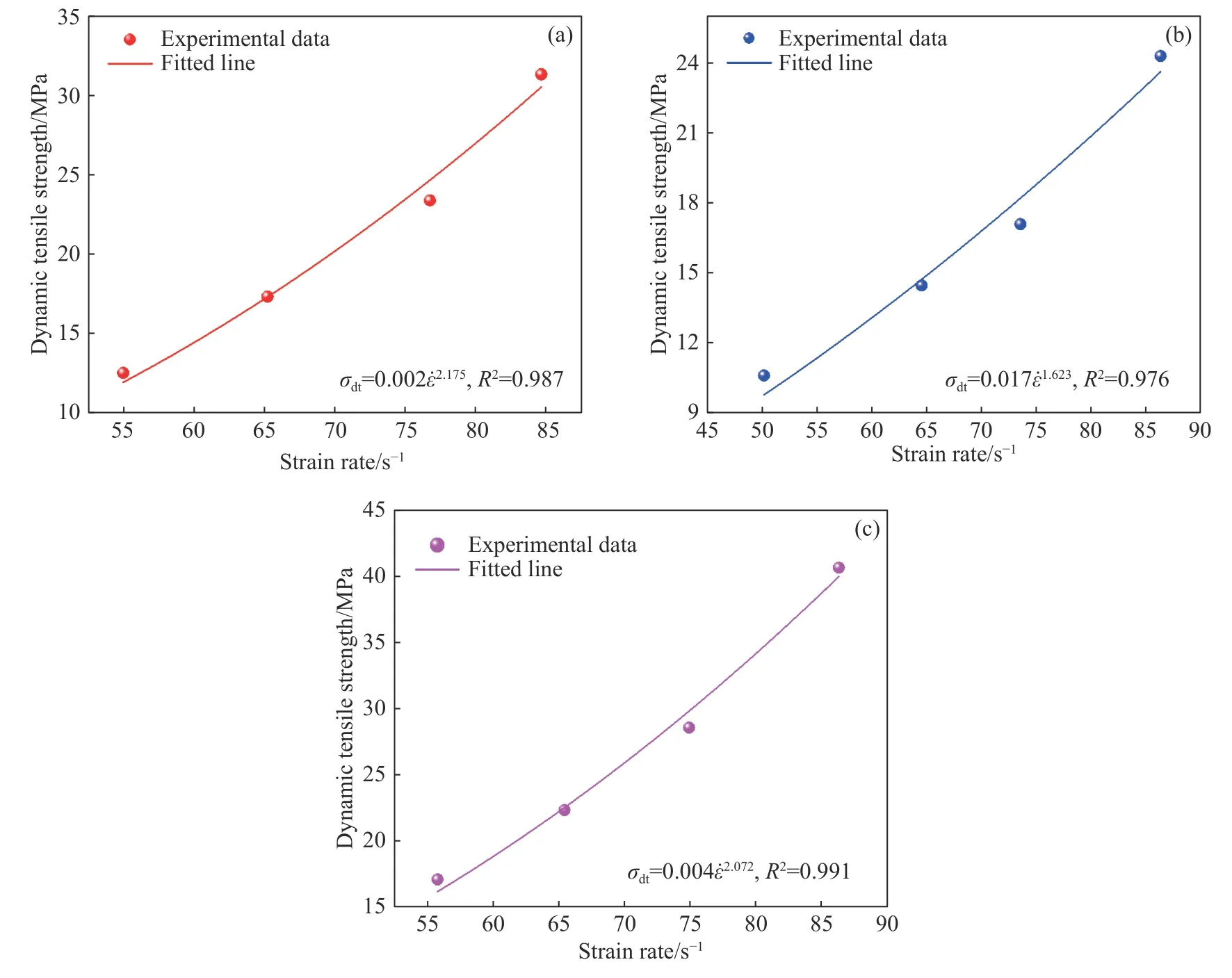
图9 不同状态岩样拉伸峰值应力的应变率效应.(a)干燥;(b)饱水;(c)冻结Fig.9 Strain rate effect of the peak tensile stress of rock samples in different states: (a) drying;(b) saturated;(c) frozen

在应变率较低的静态力学实验中，负温岩石强度的单轴、三轴强度大于常温岩石.负温条件下岩石的动态力学性能由于应变率的显著差异不同于静态.在静态或准静态实验中，岩石受压时会出现显著压密段，即冰岩间的裂隙有明显闭合过程，而动态力学实验中外力作用迅速，内部裂隙闭合和新裂隙产生几乎同时发生，因此低温动态力学性质与静态有显著差异.四种应变率下，压缩应力的冰强化因子F2分别为1.30、1.62、1.41、1.43，拉伸应力的冰强化因子F2分别为1.36、1.28、1.22、1.29，即应变率相同时，饱水岩石在冻结状态下的动态强度大于常温饱水强度[19]，这种现象有两个原因.

(1)如图11，当温度从常温降到−4 ℃附近时，水冰相变会使岩石内部产生微裂隙，内部原生裂隙也会有一定程度发展，岩石因此发生一定程度劣化，岩石孔隙内部大部分被冰所占据.随着温度继续降低至−20 ℃，岩石内部孔隙冰含量增加，随后水分迁移速率逐渐减小，导致内部孔隙冰含量趋于稳定.温度降低过程中，岩石矿物和冰由于热胀冷缩同时收缩，岩石基质收缩速度V1大于冰的收缩速度V2，内部孔隙中基质和冰之间间距缩小，岩石内部密实程度增加，动态强度增大.

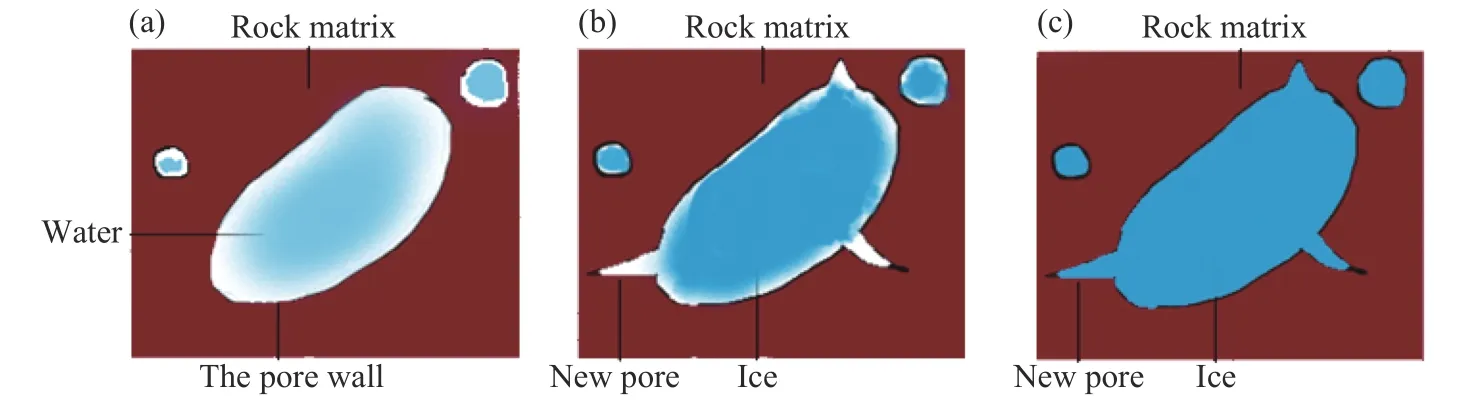
图11 岩样内部结构随温度变化示意图.(a)常温;(b)−4 ℃;(c)−20 ℃Fig.11 Variation in the internal structure of a rock sample with temperature: (a) room temperature;(b)−4 ℃;(c)−20 ℃

(2)岩石基质本身在低温冻结过程中的力学性能、抗形变能力增强，饱水冻结岩石整体强度因此增大.

实验中用于冻结试验的大理岩孔隙度0.32%，由于保鲜膜封闭作用，可忽略冻结过程中与外界的水交换，由此冻结前岩石内部含水量较低，冻结过程中产生的新孔隙、裂隙有限，由于冻胀力带来的劣化作用有限，冻结前后岩石整体性较强.推测在冻结过程中，岩石基质对温度变化较敏感，对岩石动态的力学性质改变起主要作用.

3 能耗特征

目前，针对冻结岩石的动态能耗特征的研究内容集中在入射能WI、吸收能WS、能量利用率ω等与应变率的定性结论和定量规律，岩石的动态破裂过程不仅与外载荷的强度有关，还与载荷作用时间密切相关，对冻结岩石的动态破碎时间、破碎能耗关系与应变率间的理论关系鲜有报道.根据一维应力波理论，由入、反射信号可得到入射波能量WI、反射波能量WR和透射波能量WT[22−26]：

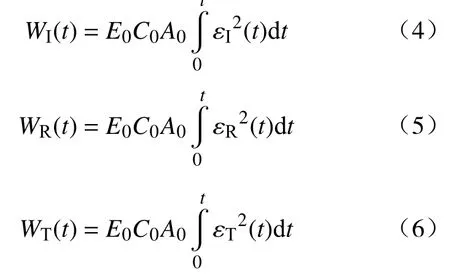
根据能量守恒定律，得到岩石试件吸收能WS：

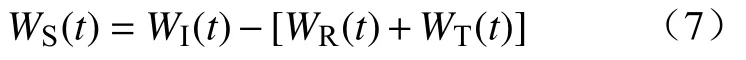
式中：E0为杆件的弹性模量;C0为杆件的纵波波速；A0为杆件的横截面积，εI、εR和εT分别为入射、反射与透射应变，t为从实验开始到计算能量时实验持续进行的时长.岩石试件吸收能WS主要包括岩石破碎耗能W、弹射动能WK和其他形式耗散能WO.W为岩石中原有裂纹扩展、产生新断面表面、岩石碎块产生新裂纹能耗，弹射动能WK为破碎试样飞出携带动能，其他耗能WO包括热能、声能和辐射能等.根据前人的实验结果，W占吸收能WS的95%左右，二者呈线性关系；弹射动能WK、其他耗能WO占比小，不易计算，因此用0.95倍WS近似替代W.

本文借用邓勇等[27]提出的岩石动态破裂所需能量的理论模型，分析比较三种状态应力岩石破裂所需时间T、破碎耗能W与应变率相关量的关系，为描述冻岩的动态破坏过程提供思考.根据该理论模型，岩石破裂所需时间T、岩石破碎耗能W由下式计算：

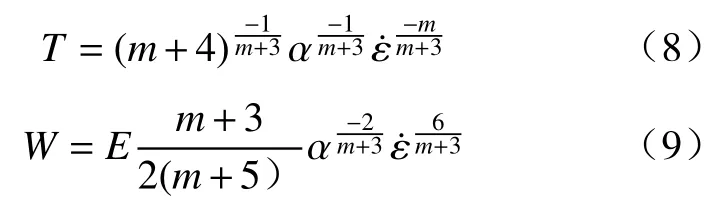
式中：E为岩石试样未损伤时的固有弹性模量，m为表征破裂活化的材料特性的常数，α为由m决定的常数，m取值由岩石破碎效果而定.由式(8)、(9)可以看出，破裂所需时间T、岩石破碎耗能W与应变率呈幂函数关系，且T与ε˙的负幂函数为线性关系、W与的正幂函数线性相关.根据动态力学实验结果得出表2，综合考虑不同情况下的T、W取参数m=4，得出常温和冻结条件下T、W与相关量的拟合关系如图12、13 所示.实验中，当且仅当m=4 时实验数据与理论模型相符合，

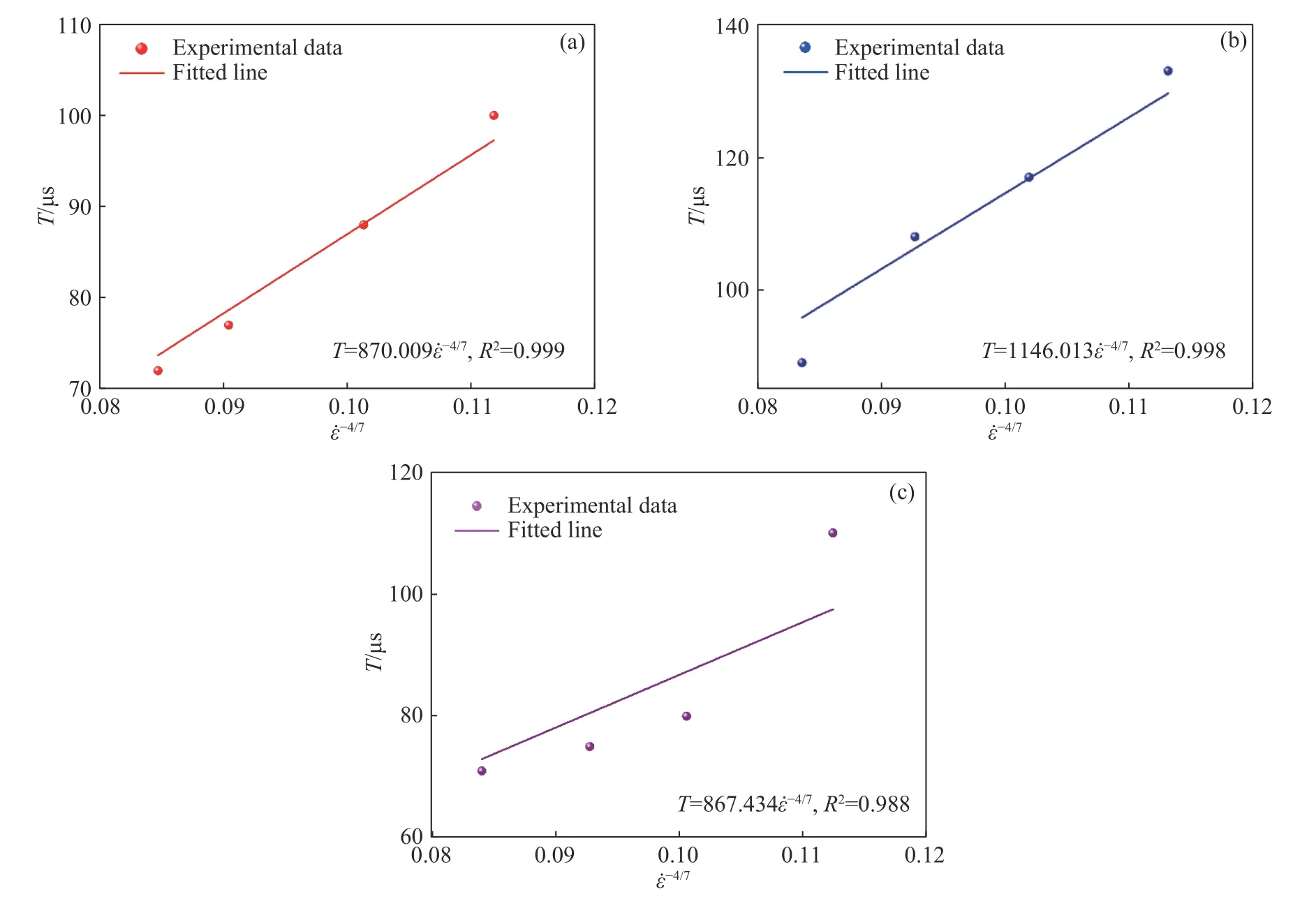
图12 不同状态岩样破碎时间与−4/7的关系.(a)干燥;(b)饱水;(c)冻结Fig.12 Relationship between the crushing time and −4/7 of rock samples in different states: (a) drying;(b) saturated;(c) frozen

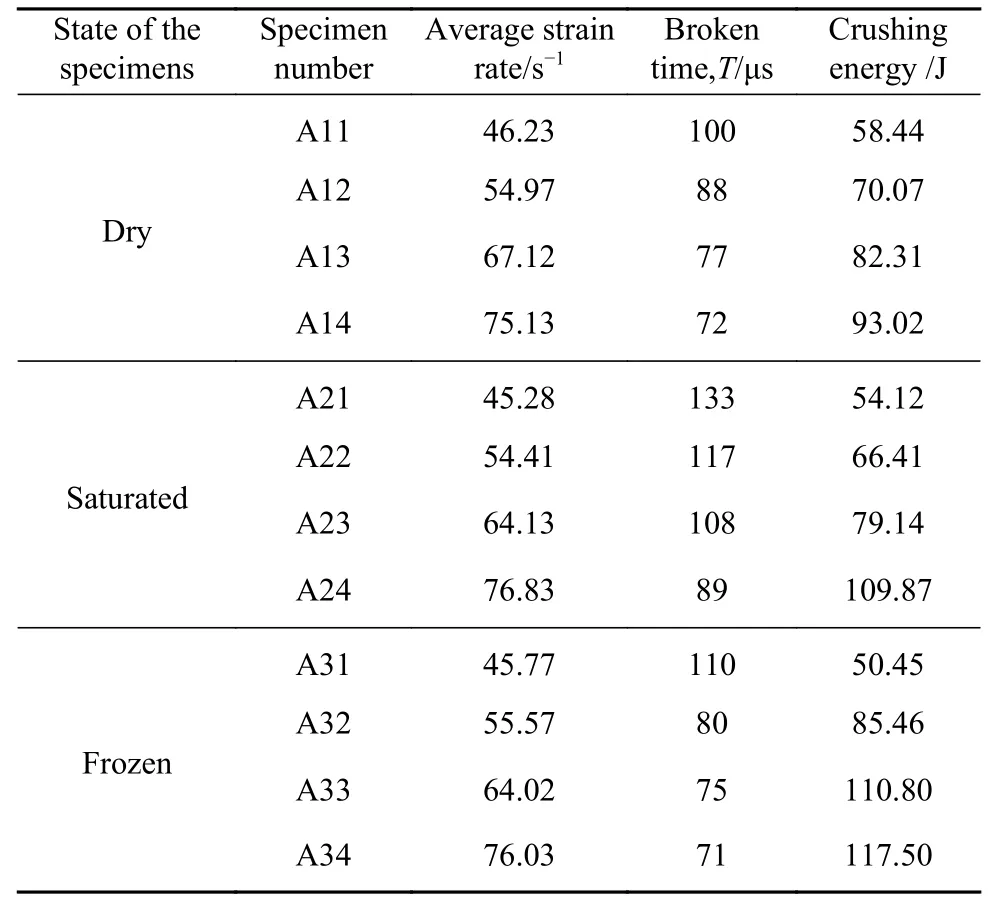
表2 岩石压缩破碎能耗计算结果Table 2 Calculation results of energy consumption for rock crushing

其中岩样破裂所需时间T由图4 表示的方法获得.

由图12可知，当m=4时不同状态岩样破碎时间T与大致呈线性关系，相同下，岩样在饱水状态下所需破碎时间最长；随升高，饱水岩石的破碎时间下降最快，说明饱水岩石的动态冲击破碎时间对最敏感.由图13可知，不同状态岩样破碎耗能W与大致呈线性关系，相同下，冻结岩样破碎耗能最多；冻结岩样破碎耗能对较敏感，变化幅度较大，而常温岩样破碎耗能相对稳定.

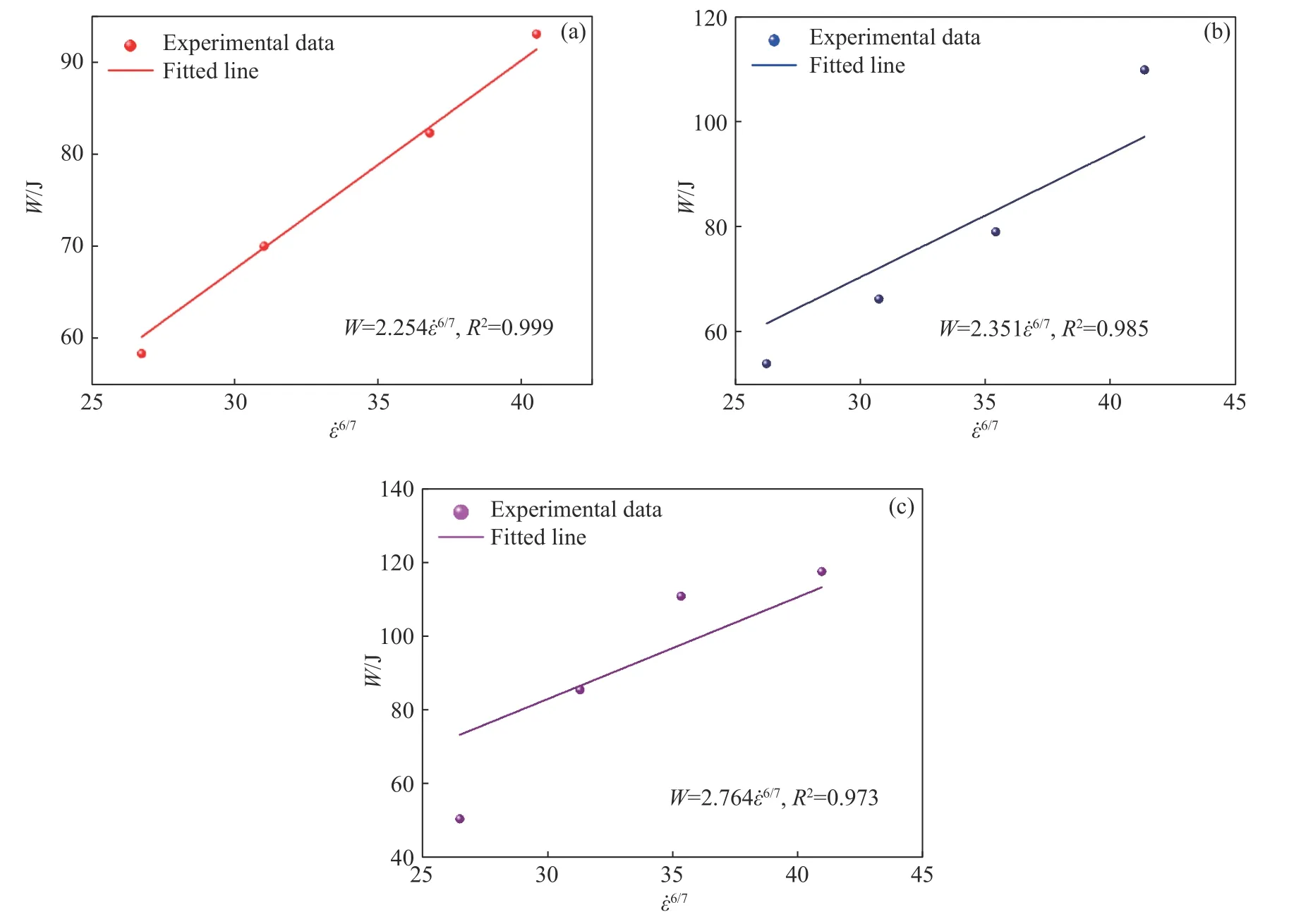
图13 不同状态岩样破碎能量与6/7的关系.(a)干燥;(b)饱水;(c)冻结Fig.13 Relationship between the crushing time and 6/7 of rock samples in different states: (a) drying;(b) saturated;(c) frozen

4 结论

(1) 同一荷载条件下，受低温水冰相变和岩石基质冷缩的共同影响（岩石基质冷缩为主要因素），−20 ℃冻结岩样的平均单轴动态压缩、拉伸强度为常温下有所增大.受孔隙水软化影响，饱水岩样动态强度小于干燥岩样，同一应变率下的实验数据大致满足 σF>σD>σS.

(2) 不同工况下的 σ-ε曲线随应变率增大的变化情况大致相同，即常温下的应力应变曲线随应变率增大的变化规律同样适用于低温.冻结大理石的初始抗变形能力强，破碎后的脆性行为较常温下稍稍延后.