基于响应面法的仔猪配奶罐搅拌器数值模拟与优化
吴壮壮,牛智有,刘梅英,刘静,李洪成
华中农业大学工学院/农业农村部智慧养殖技术重点实验室,武汉 430070
哺乳阶段是生猪养殖的关键环节,提高仔猪的成活率是决定生猪养殖产业的经济效益和社会效益的关键指标之一[1]。满足哺乳仔猪的营养摄取,及时对哺乳仔猪进行喂奶或补奶是提高仔猪成活率的重要措施。在仔猪自动喂奶设备中,仔猪配奶罐主要用于承载和制备奶水,搅拌器作为仔猪配奶罐的核心部件,主要用来促进奶水混合和加热,其搅拌性能与奶水品质密切相关。在实际生产中,由于搅拌器型式、搅拌器结构参数等因素的不合理性导致搅拌性能低下的情况时有发生。因此,优化搅拌器参数对提高仔猪配奶罐的搅拌性能尤为重要,对提高仔猪存活率具有重要意义。
传统的搅拌器研究如LDV或PIV测量技术等操作成本高、费时、费力,难以获得搅拌器对流动介质混合的流场信息[2-3]。随着计算机技术的快速发展和计算流体力学理论体系的逐步完善,CFD数值模拟为获取搅拌槽内复杂的流场信息提供了新方法[4-5]。李欣欣等[6]针对单层双桨叶采用CFD数值模拟的方法分析了单因素条件下不同搅拌器参数对混合时间、搅拌功率和单位体积混合能的影响,结果表明单位体积混合能可以作为参数优化指标。张智等[7]基于Fluent对不同搅拌器摆放角度下的流场进行了数值模拟分析,获得了不同摆放角度对搅拌效果的影响规律。王定标等[8]利用CFD技术和PIV测量研究了双层桨在不同位置的流场和浓度分布,得出了桨叶高度和加料位置对搅拌功率基本没有影响,对混合时间有较大影响的结论。贾慧灵等[9]通过对圆盘涡轮式搅拌器不同叶片倾角下的浓度场数值模拟,发现不同叶片倾角对应的最佳安装高度不同,且当安装高度降低时,搅拌釜内的流型由径向流转化为轴向流。Ranade等[10-11]采用了CFD数值模拟方法对传统的四斜叶涡轮和直叶涡轮进行了分析,结果表明该方法可以较好地反映搅拌槽内的湍流流场分布。综上所述,虽然国内外研究人员对搅拌器已有了较深入的研究,但主要集中于流场的分析,而对温度场的研究较少,尤其在综合考虑多个因素及交互作用对流场和温度场影响方面的研究缺失。因此,优化搅拌器参数,提高搅拌器的搅拌性能,建立多指标参数优化数学模型,具有重要的现实意义。
本研究在已有的研究基础上,设计一种双层桨叶仔猪配奶罐,采用CFD数值模拟与响应面分析相结合的研究方法,以双层桨叶搅拌器的转速、层间距、桨叶角度和离底距离为优化参数,以搅拌功率、混合时间和平均温升速率为响应指标,基于四因素三水平正交仿真试验计算结果,构建搅拌器参数与响应值之间的响应面回归模型,分析各设计因素及其交互作用的影响,寻求最优的设计参数组合,旨在为仔猪配奶罐中搅拌器设计提供理论参考。
1 材料与方法
1.1 仔猪配奶罐的工作原理及总体结构
仔猪配奶罐在进行仔猪奶水制备时,需要用搅拌器对奶水进行混合。根据实际需求,设计了一种双层桨叶式仔猪配奶罐,实际容积约为127 L,有效容积100 L,其主要由罐体、外夹套、搅拌装置、加热装置等组成。在搅拌装置中,选用双层桨叶搅拌器,依靠其搅拌作用,加快奶粉的快速溶解和传热。在加热装置中,采用电加热-夹套水浴加热的加热方式对奶水进行温度控制。此外,为了保证奶水的质量安全,仔猪配奶罐整体采用食品级304不锈钢材质。仔猪配奶罐结构示意图和试验台架如图1所示。
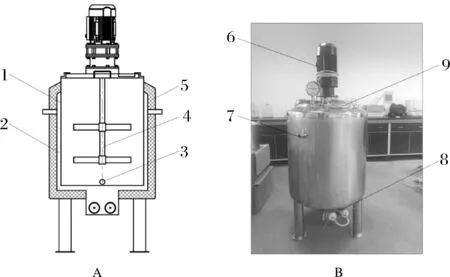
图1 仔猪配奶罐结构示意图(A)和试验台架(B)Fig.1 Structural diagram of piglet milk preparation tank (A) and test bench (B)
1.2 仔猪配奶罐数值模拟
1)物理模型构建。双层桨叶仔猪配奶罐简化模型如图2所示,配奶罐直径为500 mm,高度为600 mm,初选搅拌器直径为350 mm,搅拌器轴径30 mm,桨叶宽度35 mm,桨叶角度为90°,搅拌器离底距离为150 mm,搅拌器层间距为200 mm,转速为60 r/min。

图2 双层桨叶搅拌器简化模型Fig.2 Simplified model of double-layer paddle agitator
2)网格无关性分析。使用Mesh网格划分软件对导入的模型进行网格划分。在网格划分时采用结构化网格与非结构化网格相结合的方式,对形状规则的静止区域采用六面体结构化网格划分,对形状复杂的桨叶区采用空间适应能力较强的非结构化四面体网格,并对桨叶及桨叶区流体进行局部加密。为了更好地反映流场状态以及提高数值模拟结果精度,进行网格无关性分析。对配奶罐内5个不同速度监测点进行速度分析,网格数量从5万增加到36万,分别进行CFD数值模拟,根据分析结果选择28万作为数值模拟的网格数量。
3)边界条件设置。采用多重坐标系法(multiple reference frame, MFR)解决配奶罐内运动区域和静止区域的交互问题,将计算域划分为包含桨叶运动的桨叶区和除了桨叶区以外的静止区,2个区域通过Interface面进行数据交换。配奶罐的内壁面、下表面设定为无滑移壁面,上表面设定为对称边界。设定计算域的流体介质为奶水,奶水密度为1 062 kg/m³,黏度为8 MPa·s,比热容为3.5 kJ/(kg·℃),导热系数为0.45 W/(m∙K)。
1.3 模拟方法与模型验证
1)模拟方法。通过设置不同参数模拟不同的环境进行流场和温度场的数值分析。流场模拟采取稳态计算方法,采用标准k-ε双方程湍流模型,以SIM‑PLE算法作为压力速度耦合方式,收敛精度设定为10-4。待稳态流场收敛后,在配奶罐内的某一点加入示踪剂进行混合时间的模拟,将此稳态流场作为初始条件进行示踪剂浓度场的瞬态模拟,开启组分传输模型,仅激活组分传输项,打开示踪剂方程,关闭其他方程,设置残差收敛标准为10-7。温度场模拟采用瞬态计算方法,为了简化计算,将配奶罐内壁面和下表面设定为恒温热源360 K(86.85 ℃),桨叶区和静止区初始温度设定为300 K(26.85 ℃),能量方程残差设置为10-8,仿真时间300 s,示踪剂加料点及监测点和温度监测点如图3所示。

图3 示踪剂加料点及浓度监测点(A)、温度监测点(B)Fig.3 Tracer feeding point and concentration monitoring point(A),temperature monitoring points(B)
2)仿真模型验证。参考文献[12]验证方法,将功率准数模拟值与功率准数理论值进行比较。功率准数模拟值、搅拌功率P、功率准数理论值及雷诺数(Re)可由公式(1)~(7)计算得到[13-14],力矩可由数值模拟得到,在进行理论值计算时,双层桨叶搅拌器的功率准数可以近似看作为单层桨的功率准数乘以搅拌桨的层数[15]。经计算分析得知,功率准数理论值普遍比模拟值大,两者相差较小,但整体变化趋势相同,这是因为CFD数值模拟是基于流体各向同性的特性计算得到的,而实际中流体特性是各向异性的,因此,可以使用此模型进行数值模拟分析。
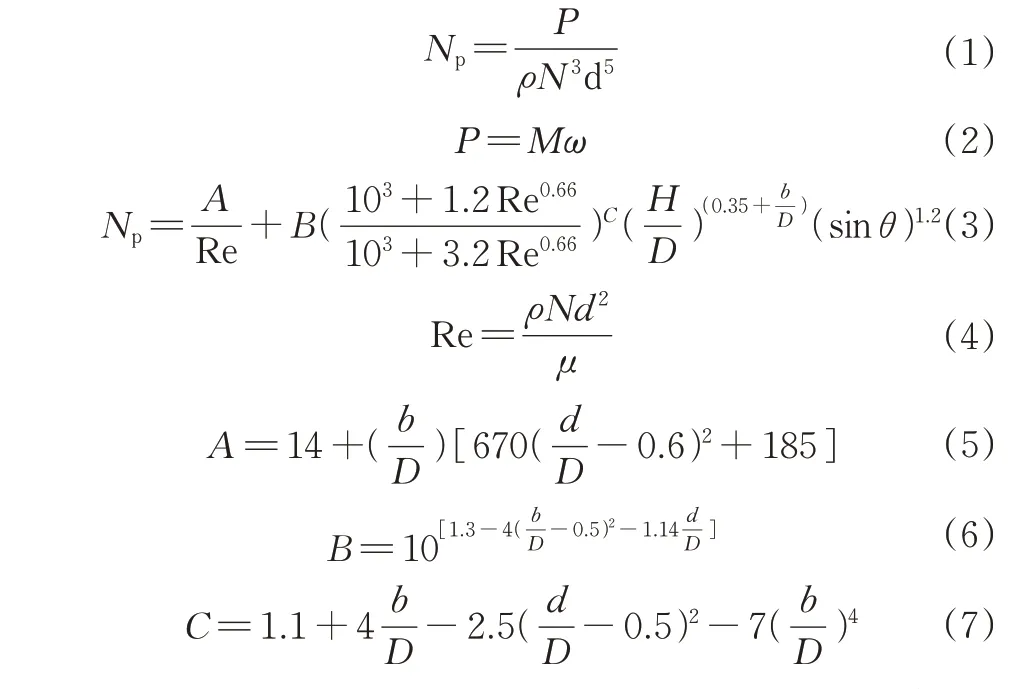
式(1)~(7)中:ω为角速度,rad/s;N为搅拌转速,r/s;ρ为搅拌介质密度,kg/m³;b为桨叶宽度,mm;d为搅拌器直径,mm;θ为桨叶角度,(°);H为液面高度,mm;D为罐体内径,mm;μ为搅拌介质黏度,Pa∙s。
1.4 搅拌评价指标
搅拌评价指标主要包括搅拌功率、混合时间、平均温升速率。理想状态下搅拌功率正好为搅拌作业功率,在搅拌系统中应合理控制搅拌功率,避免过大或过小。混合时间是指从搅拌开始到罐内液体理化特性参数不存在明显差异时的时间,国际上通常用95%的规则确定混合时间,即当一个或多个监测点达到最终稳定浓度的±5%所用的时间为混合时间。平均温升速率是平均温度与加热时间的比值,能够反映出在相同加热时间下不同搅拌器参数对温度的影响程度,平均温升速率越大,加热效率越高。
1.5 响应面法设计
本研究采用BBD法进行响应面试验设计。在响应面分析中采用二阶多项式模型,分别构建设计因素与响应指标之间的函数关系。选用的二阶多项式模型基函数为
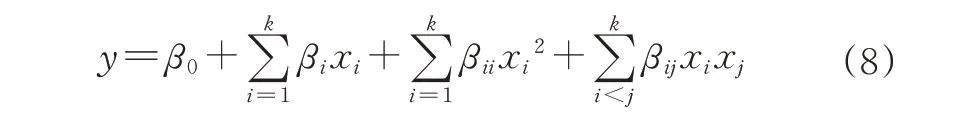
式(8)中,y为响应指标;xi、xj为设计变量;k为设计变量个数;β0为回归方程常数;βi、βii、βij分别为回归方程的线性偏移系数、二阶偏移系数和交互系数。本研究基于双层桨叶仔猪配奶罐,使用Design-Ex‑pert8.0.6软件以搅拌器转速(X1)、层间距(X2)、桨叶角度(X3)和离底距离(X4)为设计优化参数,以搅拌功率(Y1)、混合时间(Y2)和平均温升速率(Y3)为响应指标,设计四因素三水平正交仿真试验,共设计出29组试验。按照试验组的搅拌器参数分别构建不同的仿真模型并展开CFD数值模拟分析。试验因素水平如表1所示。
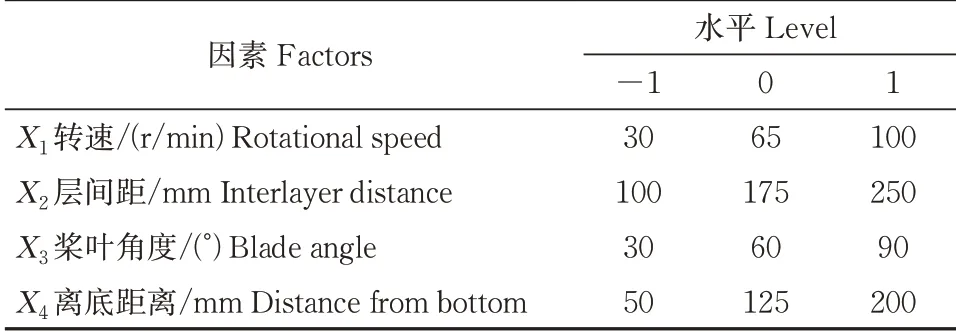
表1 试验因素及水平Table 1 Test factors and levels
2 结果与分析
2.1 仿真模型构建与网格划分
采用Design Modeler构建仿真模型,使用Mesh进行网格划分,仿真模型及网格划分示意图如图4所示。

图4 仿真模型(A)及网格划分(B)Fig.4 Simulation model (A) and meshing (B)
2.2 响应面模型建立与分析
1)响应面模型建立。BBD响应面试验设计方案及数值模拟结果如表2所示,二阶多项式响应面回归模型分别为:
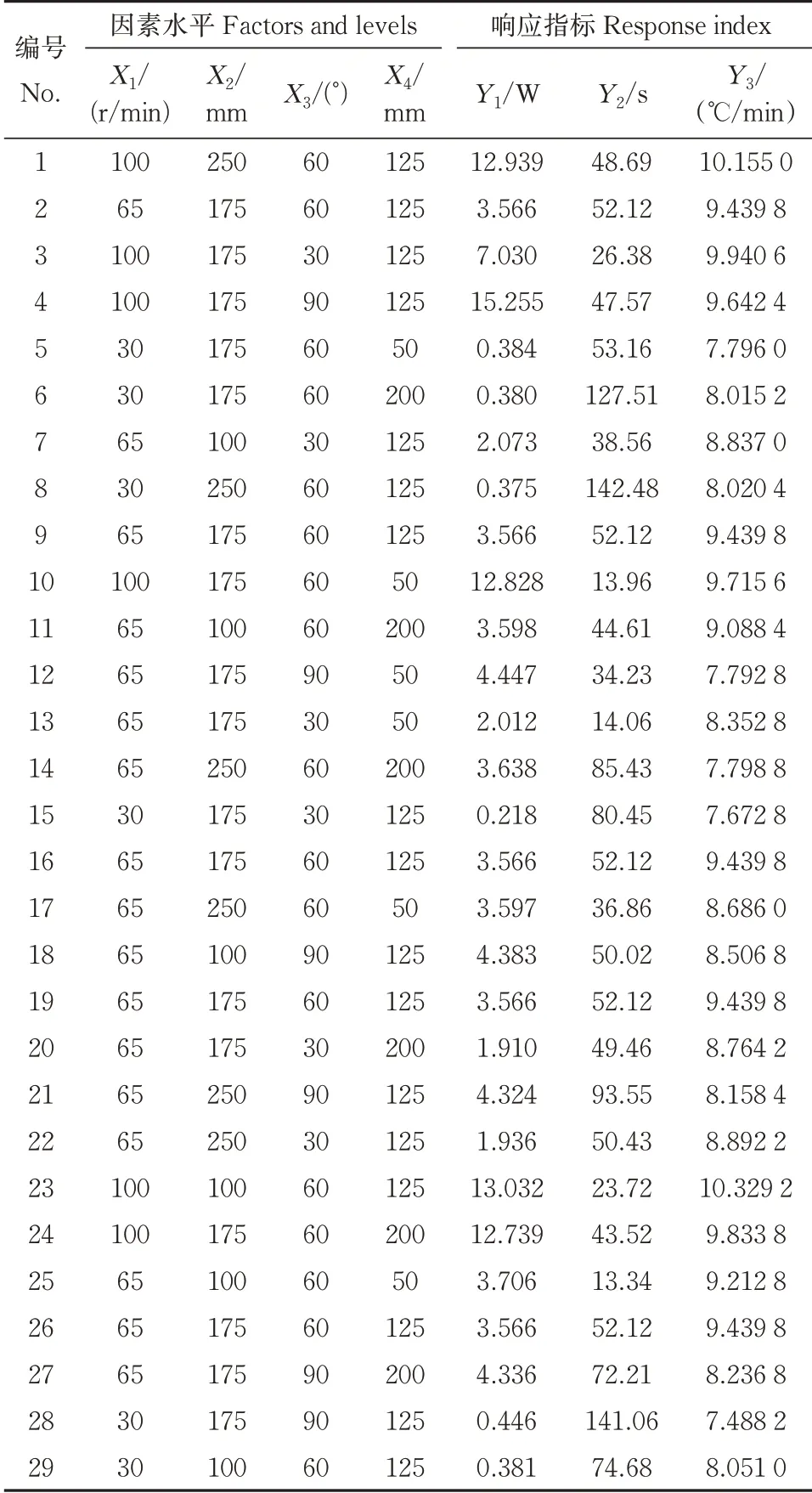
表2 搅拌器参数响应曲面试验设计与结果Table 2 Experimental design and calculation results of agitator parameter response surface
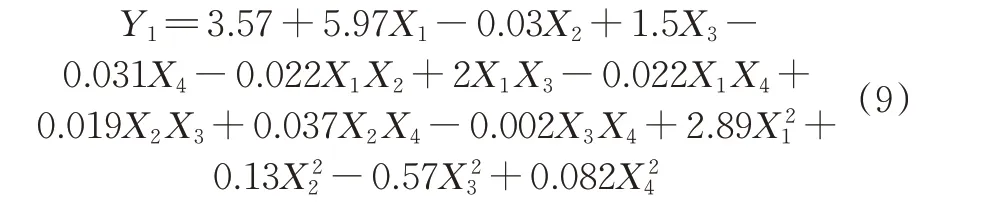
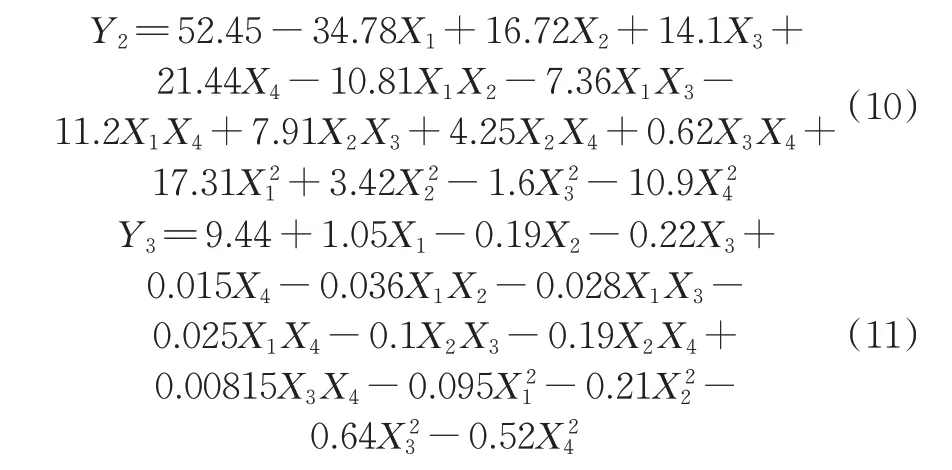
2)响应面模型方差分析。为了检验响应面回归模型拟合的准确性,采用方差分析法对设计因素与响应指标间的响应面模型分别进行显著性分析,以复相关系数R2和校正决定系数R2adj评价响应面回归模型的拟合效果,其值越接近于1,表示拟合效果越好[16]。响应面回归模型误差分析如表3所示,响应面方差分析如表4、表5和表6所示,可以看出,搅拌功率、混合时间和平均温升速率的响应面模型P值均小于0.000 1,表明响应面回归模型极显著,具有统计学意义。搅拌功率、混合时间和平均温升速率响应面模型的复相关系数R2分别为0.991 7、0.988 1、0.947 2,校 正 决 定 系 数R2adj分 别 为0.983 4、0.976 1、0.894 4,表明拟合得到的响应面回归方程拟合程度高,准确性强,预测值与实际值间具有高度相关性,可以用该模型对搅拌器相关指标进行分析及预测。

表3 回归模型误差分析Table 3 Analysis of error in regression model
由表4可知,4个设计因素中X1、X3对搅拌功率Y1响应面模型的影响均为极显著,交互项中X1X3影响极显著,二次项中X12影响极显著,X32影响显著,其余项不显著,设计参数影响大小顺序为X1>X3>X4>X2。由表5可知,在4个设计因素中X1、X2、X3和X4对混合时间Y2响应面模型的影响均为极显著;交互项中X2X3、X1X2和X1X4影响极显著,X1X3影响显著;二次项中X12、X42影响极显著,其余项不显著,设计因素影响大小顺序为X1>X4>X2>X3。由表6可知,4个设计因素中X1、X2和X3对平均温升速率Y3响应面模型影响显著,交互项中均不显著,二次项中X32、X42影响极显著,其余项不显著,设计因素影响大小顺序为X1>X3>X2>X4。
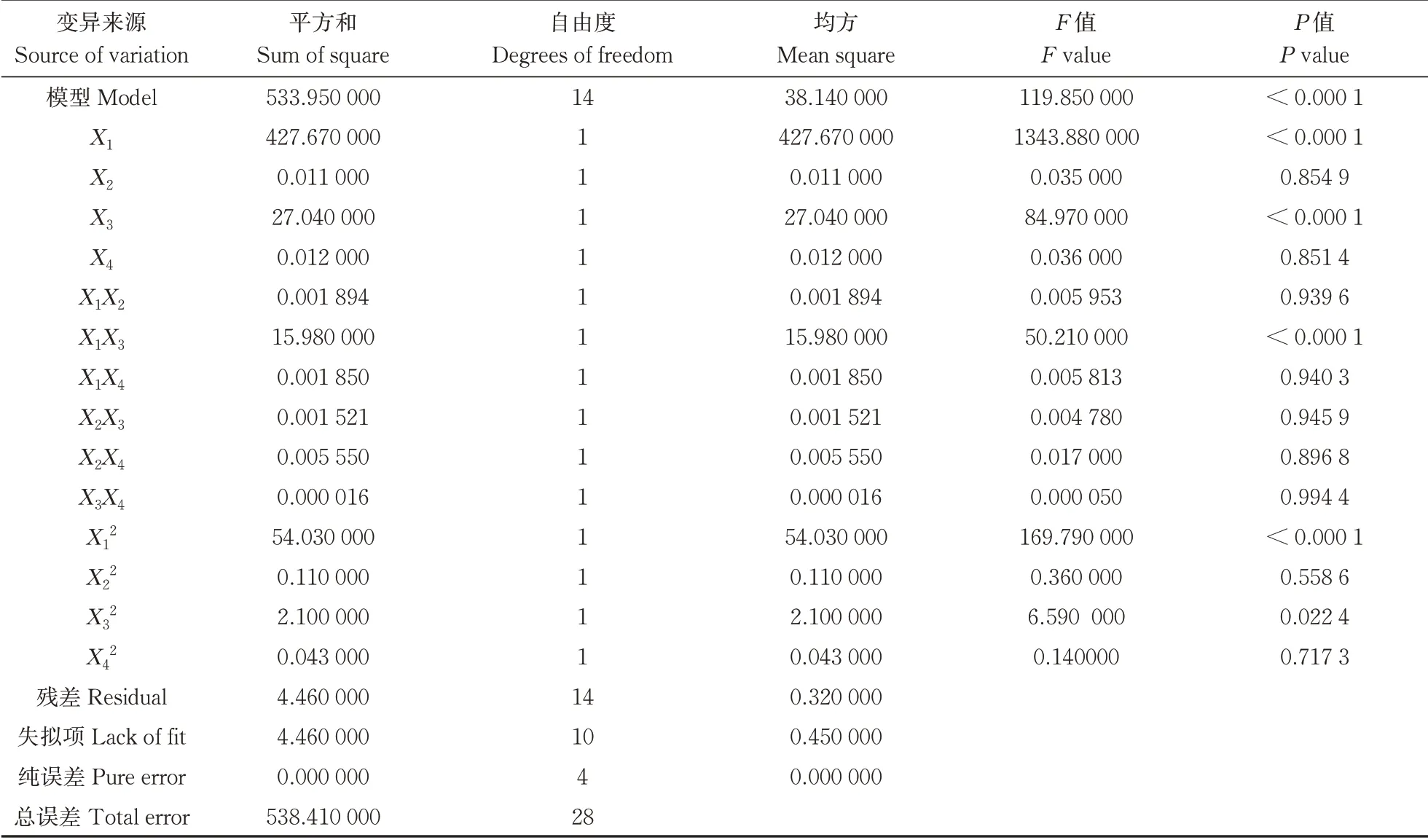
表4 搅拌功率响应曲面二次全模型方差分析Table 4 Quadratic full model variance analysis of mixing power response surface
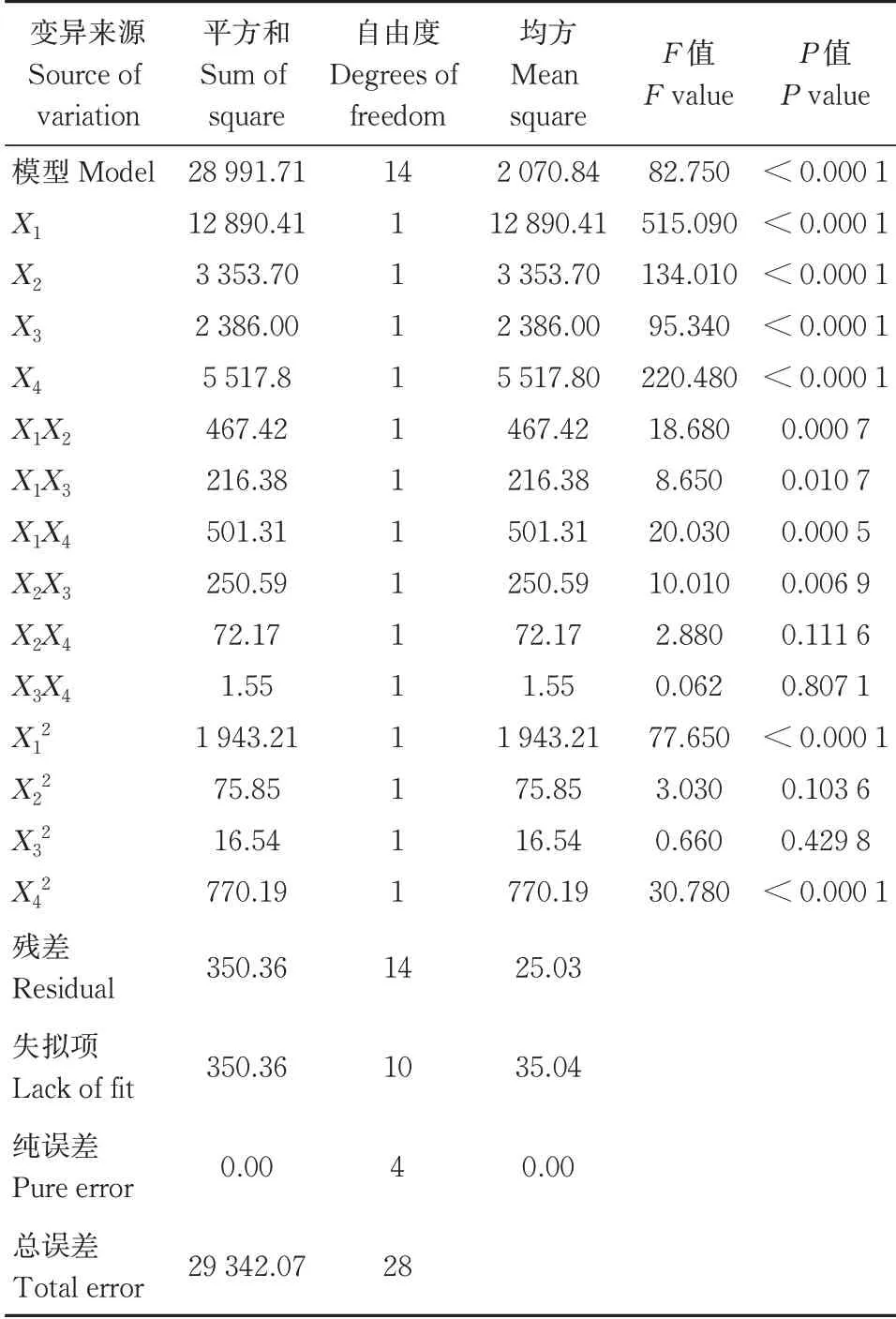
表5 混合时间响应面二次全模型方差分析Table 5 Mixed time response surface quadratic full mod⁃el analysis of variance
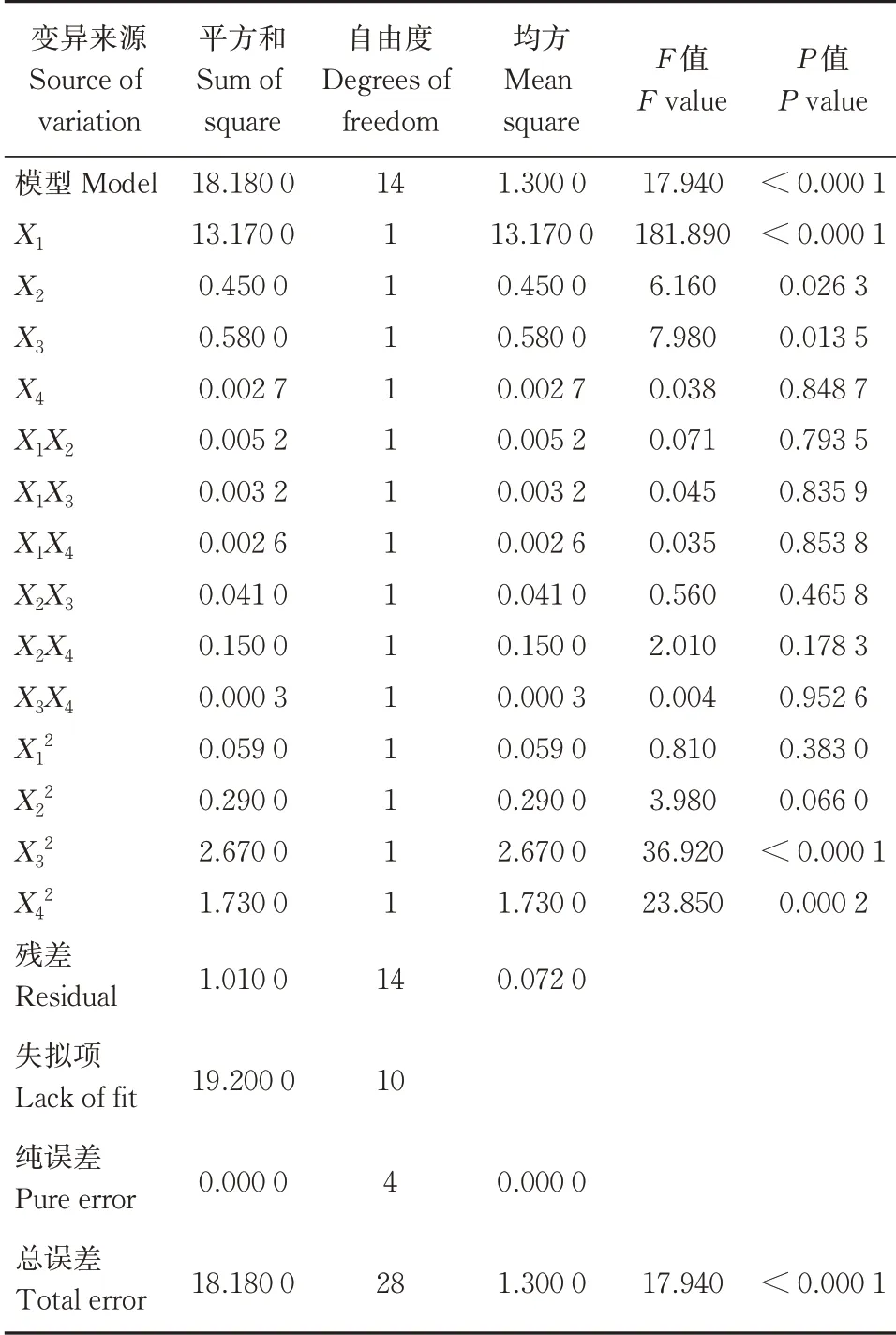
表6 平均温升速率响应面二次全模型方差分析Table 6 Quadratic full model variance analysis of mean temperature rise rate response surface
3)响应面交互作用影响。由响应面模型方差分析可知,搅拌功率响应面模型中X1X3交互作用影响显著,混合时间响应面模型中X2X3、X1X3、X1X4和X1X2交互作用影响显著,平均温升速率响应面模型交互作用影响均不显著,因此在分析因素交互作用影响时着重考虑设计参数显著交互项对搅拌功率和混合时间的影响。X1X3交互作用对搅拌功率的影响如图5所示,由图5可知,搅拌功率的大小主要受桨叶角度和转速的影响,与桨叶层间距和离底距离基本没有影响。在设计因素水平取值范围内搅拌功率随着桨叶角度和转速的增大而增大,转速对搅拌功率的影响最大。原因是随着桨叶角度的增加,搅拌器桨叶与搅拌介质的有效接触面积增加,搅拌介质对搅拌器桨叶的反作用力增大,引起搅拌力矩的增加,因此导致搅拌功率增大。而转速的增加会直接引起转矩的增加,导致搅拌功率增大。

图5 X1X3交互作用对搅拌功率的影响Fig.5 Effect of X1X3 interaction on stirring power
由图6A可知,当层间距一定时,混合时间随桨叶角度的增大而增大,层间距处于较低水平时(L=100 mm),桨叶角度对混合时间的影响相对较小,最优桨叶角度范围为30°~48°。当桨叶角度一定时,混合时间随层间距的增大而增大,桨叶角度为90°时,层间距对混合时间的影响较大,最优的层间距范围为100~175 mm,混合时间在桨叶角度为30°,层间距在100 mm时最小。由图6B可知,当桨叶角度一定时,混合时间随转速的增大而减小,转速处于30~70 r/min时,随着转速的增大,混合时间整体降低最多。转速处于70~100 r/min时,混合时间变化趋势趋于平缓且相对较小,最优的转速范围为70~100 r/min。当转速一定时,混合时间随桨叶角度的减小而减小,混合时间在转速为100 r/min,桨叶角度为30°时达到最小。由图6C可知,当离底距离一定时,混合时间随转速增大而减小。转速为85~100 r/min时,转速的增大对混合时间变化趋势影响较小,且在此转速范围内混合时间随离底距离的增大先增大后减小。由图6D可知,当层间距一定时,混合时间随转速的增大而减小。转速处于30~70 r/min时,随着转速的增大,混合时间整体降低最多。转速处于72~100 r/min时,混合时间变化平稳。当转速一定时,混合时间随层间距的减小而减小,当转速为100 r/min时,层间距的变化对混合时间影响最小,混合时间在转速为100 r/min,层间距为100 mm时达到最小。
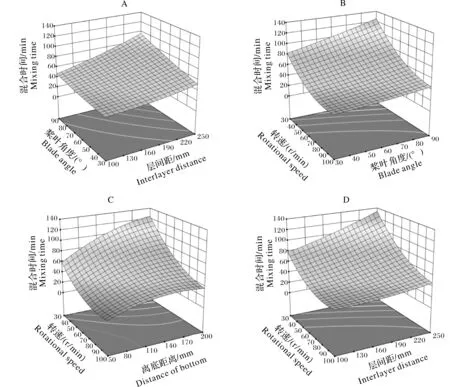
图6 交互作用对混合时间的影响Fig.6 Effect of interaction on mixing time
4)响应面模型验证。为了验证转速、层间距、桨叶角度和离底距离4个设计因素在取值范围内变化时,反映响应指标回归模型预测的准确性,在设计因素取值范围内进行随机取值,开展10组附加试验进行预测模型的精度验证,附加试验组如表7所示。
分别按照表7进行仿真模型的构建,采取与表2响应面试验组相同的操作属性开展数值模拟分析并得到数值模拟值。将表7设计因素的取值分别代入式(9)~(11)计算得到模型预测值,模型预测值与数值模拟值对比分析结果如图7所示。计算得知搅拌功率、混合时间和平均温升速率的模型预测值与数值模拟值的平均相对误差分别为9.13%、8.41%、4.08%,表明所建立的模型可以对搅拌功率、混合时间与平均温升速率进行预测。
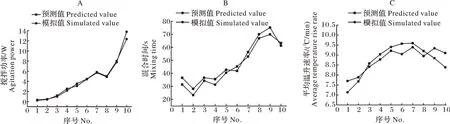
图7 预测值与模拟值对比Fig.7 Comparison between predicted and simulated values
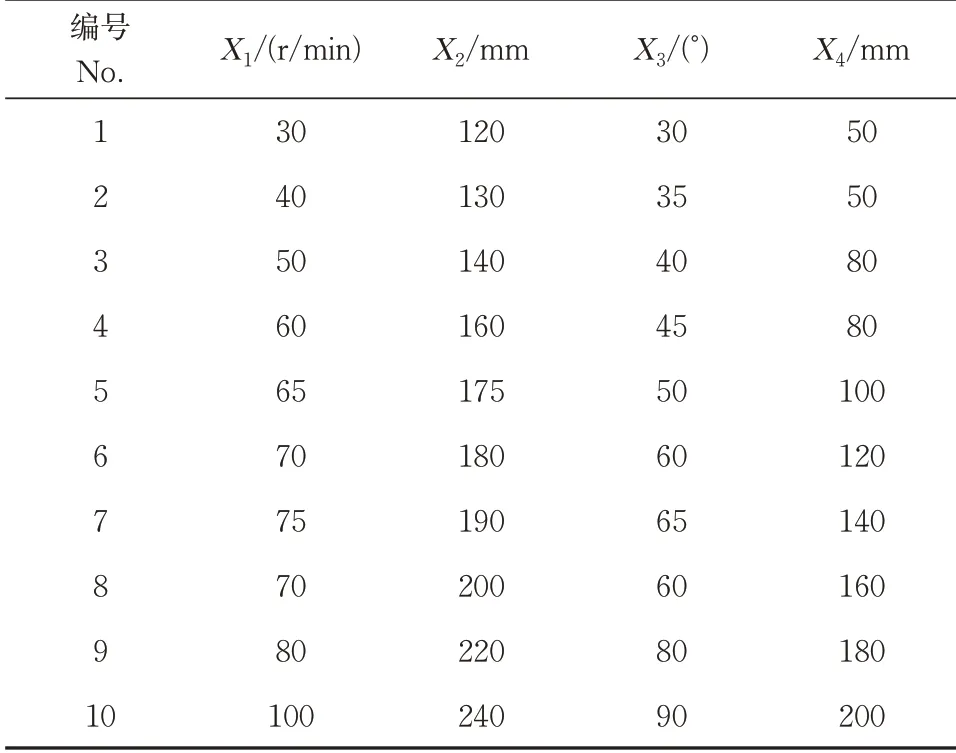
表7 附加试验组Table 7 Additional test groups
2.3 优化结果分析
以搅拌功率最低、混合时间最低和平均温升速率最高为优化目标,运用 Design Expert 软件对建立的响应指标的二次全因素响应面回归模型进行最优参数求解,约束条件为:(1)目标函数:minY1;minY2;maxY3;(2)变量区间:30≤X1≤100,100≤X2≤250,30≤X3≤90,50≤X4≤200。优 化 后 得到的各因素最优参数组合为:搅拌器转速80 r/min,层间距170 mm,桨叶角度30°,离底距离100 mm。根据最优参数结果构建仿真模型,优化前后响应指标对比分析如表8所示,可以看出,与优化前方案相比,搅拌功率减小27.08%,混合时间减小70.15%,平均温升速率提升9.57%。

表8 优化前后响应指标对比Table 8 Comparison of response indexes before and after optimization
为了进一步验证优化方案与初选方案的优劣性,分析优化前后流场湍流动能云图和温度分布云图。由图8A、B可知,优化后的流场湍流强度明显优于优化前,且湍流分布更加均匀,尤其在搅拌器的底部和近轴区湍流动能分布死区明显减小,因此优化后的模型流场分布要优于优化前的模型。由图8C、D可知,优化前的温度分布在罐体上端形成了较大的低温区,高温区主要分布在罐体底部,而优化后的整体温度分布均匀性明显优于优化前,一方面是因为优化后的模型转速的增加引起整个流体区域流速的增加,促进了流体间的热量交换,另一方面是因为优化后的搅拌器模型桨叶形状由平直叶型变为折叶型,平直叶型以径向流和切向流为主,而折叶型是以径向流、切向流和轴向流组合的混合流动,促进了近壁面温度和罐体底部的温度向罐体上端传热,使整体温度分布更加均匀。总体来看,响应面优化后的搅拌器,功率损耗减少,加热效率提高,混合强度增强,温度分布更加均匀,更适用于仔猪配奶罐。
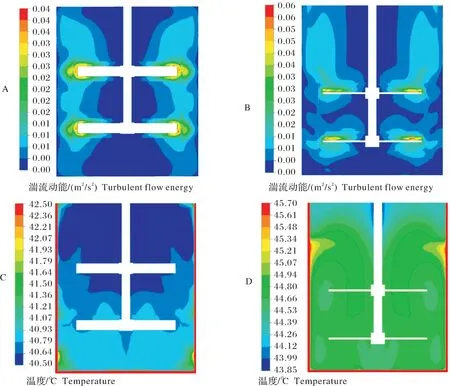
图8 优化前后湍流动能分布云图和温度分布云图对比Fig.8 Comparison of turbulence kinetic energy distribution and temperature distribution before and after optimization
3 讨论
本研究以仔猪喂奶装置中双层桨叶配奶罐为研究对象,以搅拌器桨叶转速、层间距、桨叶角度和离底距离为设计变量,搅拌功率、混合时间和平均温升速率为响应指标,基于CFD数值模拟结果建立了设计变量与响应指标间的二次多项式预测模型,分析了各因素及其交互作用对各响应指标的影响。研究表明,转速和桨叶角度对搅拌功率的影响极显著,转速、层间距、桨叶角度和离底距离对混合时间影响极显著,转速对平均温升速率影响极显著,层间距和桨叶角度对平均温升速率影响显著,其中转速是最大的影响因子。搅拌功率响应面模型中转速与桨叶角度交互作用影响显著,混合时间响应面模型中转速与层间距交互作用、转速与桨叶角度交互作用、转速与离底距离交互作用和层间距与桨叶角度交互作用影响显著,平均温升速率响应面模型交互作用影响均不显著。由响应面回归模型的误差分析及附加试验分析可知,基于二次多项式构建的搅拌功率、混合时间和平均温升速率的预测模型的复相关系数R2分别为0.991 7、0.988 1、0.947 2,校正决定系数R2adj分别为0.983 4、0.976 1、0.894 4,模型预测值与数值模拟值的平均相对误差分别为9.13%、8.41%、4.08%,表明预测模型具有较好的可靠性。基于响应面法优化得到的优化方案与初选方案相比,搅拌功率减小27.08%,混合时间减小70.15%,平均温升速率提升9.57%,湍流动能分布和温度分布相较优化前的模型有明显改善。本研究基于响应面分析和数值模拟所得到的搅拌器参数,相较优化前搅拌性能得到明显提升。但是目前仅对搅拌器进行了仿真优化,尚未进行试验研究,后续研究可以对此方面进行设计补充,综合仿真结果和试验结果进一步优化搅拌器。

