海洋环境下钢筋混凝土柱抗震性能数值模拟
周佳伟, 左晓宝
(南京理工大学 理学院, 江苏 南京 210094)
海洋工程中,钢筋混凝土柱长期处于海洋中,海水中拥有丰富的氯离子和硫酸根离子,硫酸根离子通过混凝土裂缝扩散进入内部与水泥水化物反应生成钙巩石或石膏,导致构件内部裂缝扩大,柱构件力学性能下降;随后,钢筋表面氯离子开始积聚,达到一定的浓度后破坏钢筋表面的氧化膜并开始锈蚀钢筋,导致钢筋面积逐渐减小,造成结构构件承载力降低,延性下降[1]。因此,探究侵蚀环境下混凝土构件的抗震性能退化规律对于分析结构安全性、耐久性是十分必要的。
根据已有的研究氯盐或硫酸盐侵蚀下的钢筋混凝土构件材料力学性能变化的实验成果,总结实验成果并推导出混凝土、钢筋的损伤本构模型,利用Abaqus分析软件,建立模型并模拟研究海洋环境下钢筋混凝土柱的抗震性能。目前,针对氯盐和硫酸盐对钢筋混凝土构件的侵蚀问题,国内外研究者进行了许多试验,根据实验研究成果得到了许多钢筋混凝土材料的损伤模型[2],同时对硫酸盐侵蚀作用下的钢筋混凝土构件的力学性能进行了分析[3]。研究钢筋在氯盐侵蚀作用下的锈蚀过程,结合菲克定律,得到了氯离子随着时间的变化在混凝土构件中的扩散模型,根据扩散模型推导出钢筋锈蚀量及钢筋截面积损失率的计算方程[4]。覃珊珊[5]研究了硫酸盐浓度和温度对硫酸盐侵蚀混凝土的影响规律,建立了硫酸盐侵蚀混凝土力学性能退化模型,确定了硫酸盐侵蚀混凝土材料的耐久性失效指标和失效极限状态方程,为硫酸盐侵蚀混凝土结构的耐久性设计提供了新的方法。姜磊[6]采用理论与试验相结合、宏观试验与微观分析相结合的方法,研究了干湿循环、冻融循环分别对混凝土的损伤劣化机理与性能退化规律的影响,在此基础上建立了混凝土抗压强度衰减模型与单轴受压本构模型,分析得到了损伤层混凝土的力学性能退化规律。吴莎莎[7]针对外部硫酸根离子侵蚀混凝土导致的性能劣化机制进行研究,并对该侵蚀破坏过程进行了数值模拟。Biswas等[8]考虑了钢筋腐蚀是造成混凝土和钢筋材料强度下降的重要因素,提出了一种数值模型,模拟钢筋腐蚀导致混凝土开裂后,混凝土和钢筋材料特性和两者之间粘结关系的变化,在数值分析中获得结构行为,裂纹长度和裂纹模式与实验研究非常吻合。分析结果表明,钢筋锈蚀显著降低了钢筋混凝土桥墩的结构性能。Biondini等[9]通过引入合适的材料降解规律来评估损伤。由于质量扩散的速率通常取决于应力状态,因此通过对质量传递中的随机效应进行适当建模,还考虑了扩散过程与损坏结构机械行为之间的相互作用。为了这个目标,在有限元方法框架内通过改变钢筋混凝土梁单元参数进行时间段内的非线性结构分析,通过一些应用证明了所提出的方法在处理复杂几何和机械边界条件方面的有效性。Muthulingam[10]等提出并验证了一个数值框架,该框架可以有效地量化暴露于氯化物环境的混凝土中沿钢筋周长的非均匀腐蚀渗透深度。此外,该框架考虑了钢筋尺寸和位置对氯化物进入混凝土过程的影响,并评估了与腐蚀渗透深度两种情况相对应的非均匀腐蚀状态:钢筋段腐蚀和沿钢筋不均匀腐蚀周长。计算得到的非均匀腐蚀状态与各种实验室和现场数据比较显示出良好的一致性。
前述研究中主要是针对单一影响因素对钢筋混凝土构件的作用,忽略了各因素间的耦合作用。本文研究了考虑氯盐-硫酸盐共同侵蚀下的混凝土柱抗震性能的变化规律,研究硫酸盐侵蚀对混凝土材料的损伤机理和氯盐侵蚀时钢筋截面面积变化特征,数值求解并推导得到海洋环境下氯离子和硫酸根离子在混凝土中的扩散方程,研究氯离子和硫酸根离子分布与钢筋混凝土材料损伤的关系后,以GB 50010—2010《混凝土结构设计规范》[11]中的混凝土本构为基础,得到了侵蚀作用下混凝土的本构模型及钢筋锈蚀面积方程,最后应用Abaqus有限元软件建立了考虑氯盐-硫酸盐共同侵蚀下的钢筋混凝土单柱模型,对分析结果后处理得到混凝土柱抗弯承载力、延性、滞回耗能能力等随时间变化的规律。
1 材料损伤模型
1.1 混凝土
相比未受到硫酸盐腐蚀的混凝土本构模型,实验研究显示[2]:腐蚀后的混凝土本构曲线中混凝土峰值应力、极限应力与峰值应变、极限应变都出现了下降和增大,如图1所示。本文以GB 50010—2010《混凝土结构设计规范》[11](以下简称《规范》)中提供的混凝土本构模型为基础,同时,引入损伤系数β描述硫酸盐侵蚀过程中混凝土应力-应变曲线特征参数的变化规律[3]。受到硫酸盐侵蚀的混凝土损伤本构模型如下:
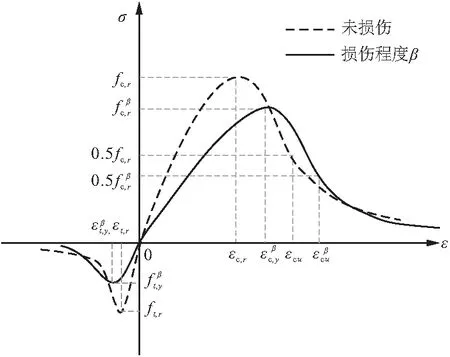
图1 混凝土损伤本构模型
(1)

(2)

(3)

混凝土柱受到硫酸根离子的侵蚀作用时,离子通过空隙和裂缝与混凝土中水泥石的一些成分发生化学反应生成膨胀性产物,从而产生膨胀应力破坏混凝土,因此硫酸根离子浓度与混凝土的损伤系数β关联密切,文献[12]基于混凝土腐蚀试验结果,对试验数据拟合后给出了混凝土损伤系数β与硫酸根离子浓度之间的关系:
(4)
式中:β(ni,t)为第ni层混凝土在t时刻的混凝土损伤系数;t为腐蚀时间;t0为混凝土初始腐蚀时间;tu为混凝土完全失效时的时间;qc为混凝土蚀强率系数,本文按照文献[13]取值,C=C(ni,t)为第ni层混凝土在t时刻的硫酸根离子浓度。
基于Fick定律和质量守恒定律,得到混凝土柱截面硫酸根离子浓度分布方程,方程[14]如下所示:
(5)
式中:kv为硫酸根离子与混凝土内部物质发生化学反应的速率常数,按照文献[15]取值;CCa为混凝土内部的钙离子浓度,按照文献[15]取值;Cs为环境中的硫酸根离子浓度,按照文献[16]取值;Ds为混凝土中硫酸根离子有效扩散系数,采用文献[17]中的公式计算确定。
1.2 钢筋
钢筋混凝土中的钢筋发生锈蚀,锈蚀的原因可以分3种[18]:氧气扩散、碳化和氯离子扩散。氯盐的侵蚀作用,是海洋环境下钢筋锈蚀的主要原因。环境中的氯离子在浓度梯度的作用下,通过混凝土的宏观、微观裂缝到达混凝土和钢筋交界面,累积到一定浓度后导致钢筋锈蚀及钢筋有效面积减少。腐蚀过程钢筋的有效截面面积按照以下公式计算:
Aeffective(t)=A0(t)-Ar(t)
(6)
式中:Aeffective(t)为钢筋混凝土结构腐蚀时间t时刻钢筋的有效截面面积;A0(t)为未受到腐蚀时钢筋截面面积;Ar(t)为腐蚀时间t时的钢筋锈蚀面积。
研究氯盐侵蚀环境下钢筋的锈蚀过程,可以知道钢筋的锈蚀分为两种[19]:均匀锈蚀和点蚀。根据氯盐造成的钢筋锈蚀特征,分别对均匀锈蚀和点蚀面积进行计算,得到在t时刻钢筋腐蚀面积Ar(t)可以按照下式计算:
Ar(t)=Aar(t)+Apr(t)
(7)
式中:Aar(t)为t时刻的均匀锈蚀面积;Apr(t)为t时刻的点蚀面积。
根据图2,可获得钢筋截面的均匀锈蚀面积为:

图2 锈蚀钢筋截面模型
(8)
式中:d0为未锈蚀时的钢筋直径;Δd(t)为钢筋锈蚀前后的直径差值;d(t)在t时刻锈蚀后的钢筋直径,d(t)=d0-Δd。
结合法拉第定律,确定钢筋锈蚀厚度与电流密度及时间之间的关系:
(9)
式中:vs为钢筋锈蚀速率,按文献[20]取值;icor为钢筋的腐蚀电流密度,按照文献[13]取值;tcor为钢筋锈蚀的开始时间:
(10)
式中:X为混凝土保护层厚度;D0为混凝土构件服役时间为t0时,氯离子有效扩散系数;t0为混凝土的初始服役时间,一般取值养护时间;m为常数,一般取0.1;Φ为标准正态分布函数;Ccr为钢筋钝化膜破坏时氯离子的浓度,按照文献[21]取值;Ccl为环境中的氯离子浓度,按照文献[16]取值。
根据图2所示的钢筋各区域的面积,结合相应参数,得到发生坑蚀的钢筋面积计算公式:
(11)
式中:θ1为坑蚀边弧线ADC对应的圆心角;θ2为与弧线ABC相对应:
(12)
式中:hp(t)为钢筋表面发生坑蚀后的的深度;q为用于表征坑蚀和均匀锈蚀的关系,一般取两者腐蚀的深度比值为6[22]。
综上所述,得到在不同腐蚀时间段内混凝土柱内钢筋的有效截面面积公式为:
(13)
2 腐蚀混凝土柱的有限元建模
2.1 基本假定
有限元建模时,作如下基本假定:
(1)在加载和受侵蚀时,柱截面始终符合平截面假定;
(2)各20 mm厚的单层混凝土的损伤系数及本构模型相同;
(3)忽略硫酸盐、氯盐侵蚀产物对离子传输及钢筋 - 混凝土位置的关系的影响;
(4)柱截面各层混凝土的接触面不发生相对位移和变形;
(5)柱截面中混凝土层的损伤系数达到0.98时认为其已经失效。
2.2 柱截面划分
根据柱截面尺寸及混凝土等效腐蚀深度,混凝土柱截面按照不同的损伤参数划分出相应的层数,将混凝土柱构件按照20 mm的间距由外向内进行等距划分,则混凝土柱被划分成15层,对未腐蚀和完全腐蚀的混凝土层进行归并,如图3所示。
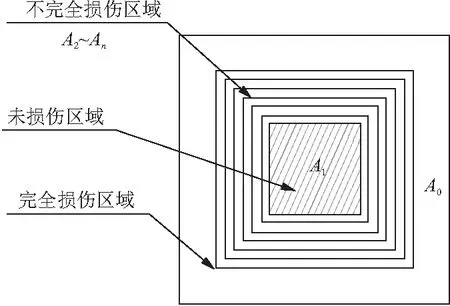
图3 构件截面划分示意
图3中A0代表在服役时间内混凝土损伤系数大于0.98的区域;A1代表未受到腐蚀,损伤参数为0的区域;A2~An为混凝土损伤系数位于区间(0,0.98)的不完全损伤区域,各层的厚度为20 mm。
2.3 Abaqus计算模型建立
2.3.1 混凝土模型
按照20 mm的间距对柱截面进行分层划分,各层混凝土的损伤程度由其所在的柱截面位置由式(5)确定截面各位置的离子浓度分布,由式(4)确定离子浓度和损伤系数的关系,再利用式(1)~(3)确定柱截面上各层混凝土的损伤本构关系。
为了分析硫酸盐侵蚀作用下混凝土柱力学性能的退化规律,在Abaqus软件中建立了腐蚀混凝土本构模型。本文对钢筋混凝土柱构件进行有限元分析时,混凝土的模型采用Abaqus软件中的塑性损伤模型,简称CDP。
2.3.2 钢筋模型
模型中锈蚀后钢筋的力学性能无变化,但是钢筋的有效面积降低。钢筋锈蚀的初始时间按式(10)计算,钢筋截面面积可按式(13)计算。加载过程中钢筋本构模型如图4,5所示。
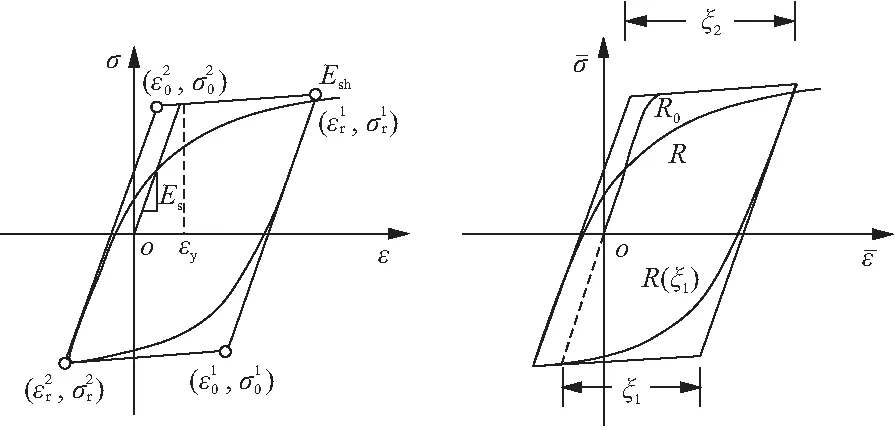
图4 Menegotto-Pinto钢筋本构 图5 曲率参数R图示
Menegotto-Pinto钢筋本构关系如图4所示,上标数字代表荷载循环次数,每一次应变反向,该类参数都要进行更新。Menegotto-Pinto钢筋本构曲线的表达式如下:
(13)
(14)
(15)
(16)
(17)
式中:σ,ε分别为当前的应力、应变;σ0,ε0分别为初始状态应力、应变;σr,εr分别为应变反向点的应力、应变;σ*,ε*为初始刚度Es发展至Esh之间的过渡应力、应变;a1,a2,R0需要根据实验确定,子程序将根据钢筋种类自动赋值。
曲率参数R如图5所示,R反映了Bauschinger效应的程度大小,R0为首次加载时R的初始值;ξ为当前循环半周期的塑性应变,每次应变反向后根据公式(18)更新:
(18)
式中:εm为加载历史的应变极值;εy为钢筋的屈服应变。
综合考虑各钢筋模型的优缺点,本文钢筋采用方自虎教授开发的M-P钢筋模型子程序[23],该本构关系不仅能很好的模拟钢筋混凝土柱的强度和刚度,模拟得到的滞回曲线与反复加载实验结果也显示出良好的一致性。Abaqus中钢筋采用Truss单元并将其通过Embedded Region方式嵌入混凝土柱中。钢筋材料子程序需要输入三个参数:钢筋初始刚度Es、屈服强度fy及硬化刚度与初始刚度的比值Esh/Es,本文Esh/Es取值0.001。
2.3.3 分析流程
利用Abaqus软件中实体单元,建立考虑氯盐、硫酸侵蚀作用的混凝土柱模型,分析过程如图6所示。
3 混凝土柱算例
3.1 模型信息
本算例目的是研究在氯盐和硫酸盐共同侵蚀作用下,混凝土单柱抗震性能的变化特性,将前述中得到的考虑侵蚀作用的混凝土本构模型和钢筋有效截面面积嵌入到Abaqus软件中,通过在柱顶施加轴向力和水平荷载,研究混凝土柱的抗弯能力、滞回曲线随腐蚀时间的变化规律。构件配筋见图7a,荷载模型如图7b所示,氯离子浓度Ccl和硫酸根离子浓度Cs采用实际海洋环境的数值[16],本算例的主要参数如下所示。

图7 混凝土柱模型及荷载图示
(1)构件、混凝土、钢筋、环境及其他参数见表1~5。

表1 构件参数

表2 混凝土参数

表3 钢筋参数

表4 环境参数

表5 其他参数
(2)计算参数:截面上各层混凝土厚度s取20 mm,时间步长Δt取10 d。
(3)加载方式:为了防止出现应力集中,在模型柱顶创建参考点并和柱顶表面耦合;采用位移的方式逐渐加载,每级位移为10 mm,加载模式如图7c。
3.2 数值模拟结果分析
3.2.1 受压承载力

(19)
式中:βi为各层混凝土的损伤系数代表值;S为混凝土柱的全截面面积;Nu0为未腐蚀柱的受压承载力;Nu为服役中混凝土柱的受压承载力;Ap为钢筋在侵蚀过程中损失的截面面积;A0为未腐蚀的钢筋的截面面积。本文将混凝土柱构件有限元模型计算得到的荷载 - 位移曲线上的峰值作为受压承载力。
图8给出了不同服役时间下,受到侵蚀作用的钢筋截面损失率、混凝土截面平均损伤系数及柱受压承载力随时间变化曲线图。由图可知,未受到侵蚀时,柱受压承载力Nu0=13852 kN,在0~10年期间,构件承载力退化较为平缓;服役10~30年期间,构件受压承载力极速下跌;30~50年期间,构件呈现缓慢下降的趋势;服役时间达到50年时,柱截面混凝土平均损伤系数达到69.9%,钢筋有效截面面积下降至39.9%,钢筋混凝土柱受压承载力下降了近65%,如果构件继续服役,安全性可靠性已经很难满足要求。总体看来,随着服役时间的增加,钢筋混凝土柱的受压承载力先期缓慢下降,后期下降速度加快。
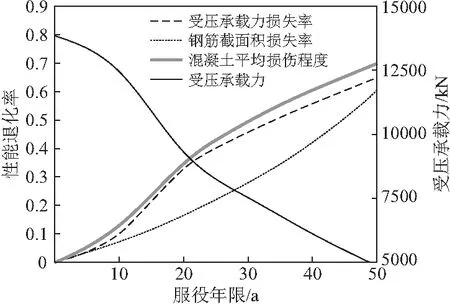
图8 侵蚀环境下柱的受压承载力变化曲线
分析上述现象产生的原因:初始服役阶段,混凝土构件受侵蚀时间较短,构件内硫酸根离子浓度较低,混凝土平均损伤程度上升缓慢。对钢筋截面积损失率而言,曲线斜率也是先平缓后陡然上升,可见钢筋锈蚀率也呈现先慢后快的趋势,初始阶段混凝土单柱受压承载力退化速度慢;随着服役时间的逐渐增长,硫酸根离子浓度在混凝土柱截面由外向内逐层递减,因而外层混凝土损伤系数增长快,而内部混凝土损伤系数增长较缓慢,当外部混凝土损伤系数达到1,即外层混凝土失效后,内部混凝土损伤系数的增长速率对混凝土平均损伤系数发展速率起主要作用,因此混凝土平均损伤系数增加速率呈现由快到慢的变化规律。
混凝土柱构件受压时,由钢筋和混凝土协同承载,根据轴向压力、钢筋端部和混凝土表面应力分布,能够得到钢筋和混凝土受压过程中各自分担的轴向压力,图9描述了N=3000 kN,材料承担轴向荷载比率的变化。从图中看出,随着构件服役时间的增加,混凝土和钢筋承担轴向荷载的比率分别呈现出降低和增加。初始,混凝土和钢筋各承担了93.3% 和 6.7%的轴向力,服役50年后,混凝土承担轴向力比率下降到78%,而钢筋承担轴向力比率上升到22%。产生上述现象的主要原因是随着硫酸根离子浓度的不断增加,混凝土截面外部的损伤系数增加使得混凝土峰值应力逐渐下降,混凝土的刚度减弱,而钢筋的刚度变化不大,因此在横截面上,随着服役时间的推移,混凝土和钢筋的承载率分别呈现下降和上升的规律。
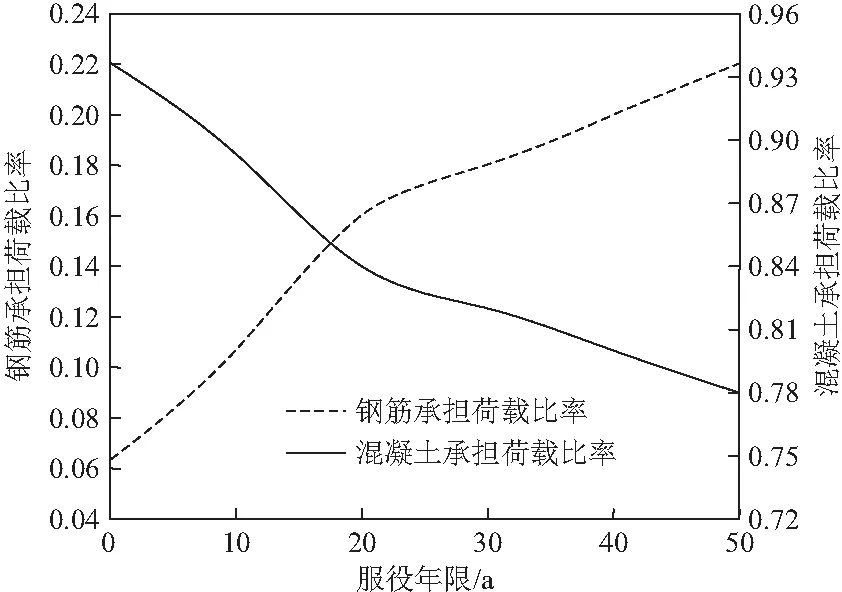
图9 材料承担轴向荷载比率变化曲线
3.2.2 受弯承载力
图10a~10c分别表示轴向力为0,1000,2500 kN时,整个服役周期内的混凝土柱顶水平荷载 - 位移曲线,表6给出了构件不同服役时间不同轴向力作用下水平荷载、柱顶位移以及延性系数。
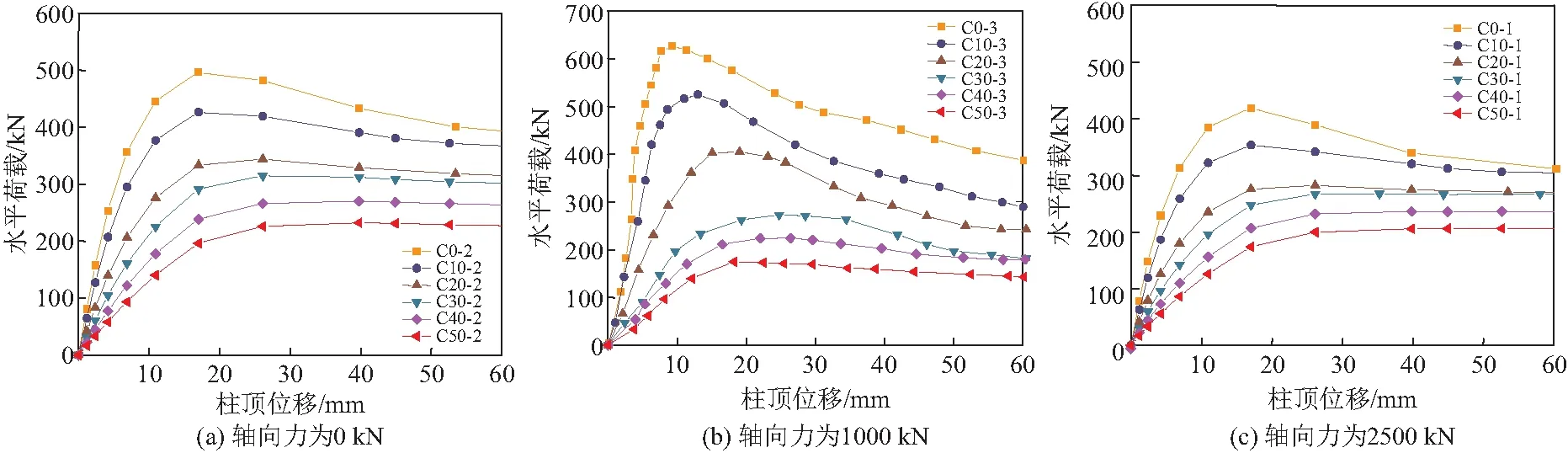
图10 不同轴向力作用下柱顶水平荷载 - 位移曲线
由图10a~10c可知,轴向力相同时,随着混凝土构件服役时间的增加,钢筋截面面积减小和混凝土平均损伤系数的逐渐增大,构件受弯承载力逐渐降低,构件的刚度也随之降低;对比服役时间0,10,20年的曲线可以发现,在服役初期阶段,适当的轴向力使得构件的抗弯承载力增强,在达到极限承载力后,承载力退化速率明显加快。当构件服役超过30年,施加轴向力会使得受弯承载力下降。上述规律产生的原因,构件服役时间增加,混凝土损伤系数增大,即使在恒定轴向荷载作用下,混凝土截面的有效面积减小,混凝土柱的真实轴压比达到一定数值后,单柱的受弯承载力基本不再增强;加载过程中柱顶水平位移后产生的二阶效应,使得构件在柱顶的轴力增大后刚度反而迅速下降。
图11为不同轴向力作用下,构件的延性系数时变曲线。分析表6和图11中各工况下混凝土单柱的位移延性系数可以看出:服役时间相同时,构件延性随着轴向力的增加而降低;当轴向力恒定时,整个服役周期内,构件的延性系数随着服役时间的增加先增后减,主要原因是初始服役时,混凝土承担大部分的轴向力,混凝土损伤系数提高了混凝土的极限压应变,因此混凝土能承受较大变形。随着服役时间继续增长,部分混凝土损伤系数增大至混凝土失效,钢筋承载率增加,损伤混凝土压碎或钢筋加载至极限压应变后,构件破坏失效,变形能力不足,延性急剧下降。
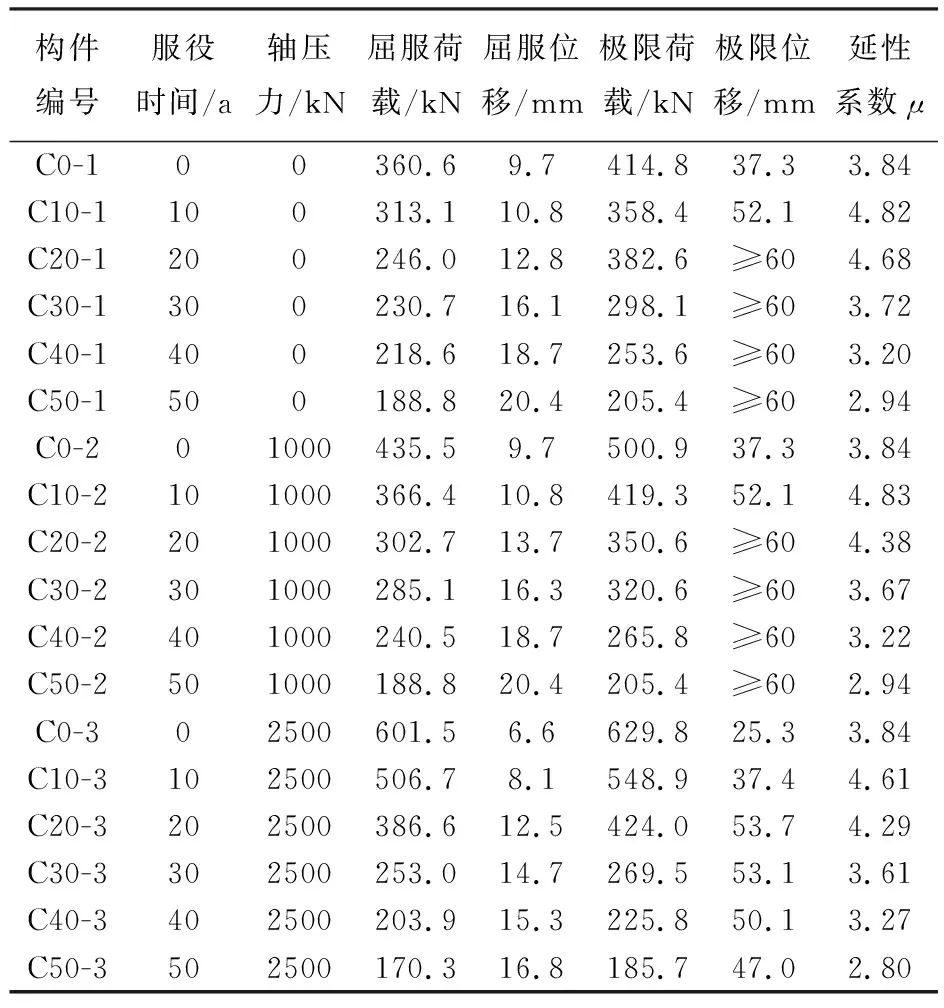
表6 柱顶水平力 - 位移模拟结果

图11 不同轴向力作用下构件延性系数时变曲线
3.2.3 抗震性能
为了研究在地震作用下,受到侵蚀的混凝土柱各项力学性能的变化规律,通过对柱顶施加低周反复荷载,得到了不同腐蚀年限下结构的荷载 - 位移滞回曲线,解析滞回曲线可以得到混凝土单柱的抗侧刚度、变形性能和耗能能力等参数随时间变化的规律。由于计算结果较多,图12给出部分服役时间水平荷载 - 变形曲线。

图12 不同腐蚀年限混凝土柱滞回曲线
由图12可知,初始加载过程中,荷载 - 位移曲线均趋近直线,随着加载位移增大,滞回曲线面积逐渐增大,此过程中的各个滞回曲线倾斜程度增加,出现了不同程度的捏缩现象;随着多次低周反复加载至混凝土峰值应力后,柱构件最大水平位移对应的荷载值逐渐下降。
图12纵向对比,即轴力相同时,可以观察到服役初期,柱的滞回曲线较为饱满,构件延性好,滞回耗能能力强,构件的变形能力强,抗震性能良好,此时滞回曲线倾斜程度小,构件的弹性性能好,刚度大。构件服役后期,结构的整体损伤程度不断增加,滞回环逐渐捏缩,耗能能力降低,抗震性能下降。
图12横向对比,即服役时间相同时,可以发现在服役初始时期,适当的轴向力一定程度增强了柱抵抗水平荷载的能力,对于服役时间较长的构件,混凝土损伤系数不断增大,外层部分混凝土已经失效,柱截面有效面积减小,构件抵御水平荷载的能力将会降低,尤其高轴向力作用下的构件刚度退化速度更快,耗能能力相对于同时间其他构件也降低了许多。随着服役时间增长,这种效应也更加明显,滞回曲线越来越向横轴倾斜和捏缩,表明构件的抗侧刚度逐渐降低,损伤程度进一步增加,抗震性能也急速下降。
4 结 论
本文总结了钢筋混凝土构件在硫酸根离子和氯离子共同侵蚀作用下混凝土和钢筋材料的力学性能变化规律,通过公式推导建立了考虑侵蚀作用的混凝土本构和不同时间段钢筋截面积变化公式,在Abaqus中建立了侵蚀环境下的混凝土单柱模型,计算分析了在不同工况下混凝土柱抗震性能变化规律。对计算结果进一步处理后,得到如下结论:
(1)氯盐 - 硫酸盐腐蚀环境中混凝土柱受压承载力的衰减先快后慢,钢筋承受荷载的比率逐渐上升,而混凝土的承载率逐渐下降。
(2)长期处于侵蚀环境中的混凝土柱构件,其抗弯刚度逐渐下降,腐蚀初始阶段,构件变形能力得到提高,达到一定年限后开始下降;腐蚀初始阶段,柱端施加合适的轴向荷载能够增加柱的受弯承载力,腐蚀年限较长时,柱的抗侧刚度迅速下降,承载力也明显下降。
(3)腐蚀初始阶段,柱构件的滞回曲线宽厚饱满,构件变形能力和延性提高;受侵蚀时间较长时,混凝土柱的滞回曲线变窄并向横轴逐渐倾斜,柱构件的变形能力和耗能能力明显减弱。

