业主与全过程工程咨询方的信息共享博弈
孙钢柱, 昝晓方, 严亚丹
(郑州大学 水利与土木工程学院, 河南 郑州 450001)
在我国建筑业持续健康发展并与国际社会全面接轨的背景下,全过程工程咨询(简称“全咨”)模式应运而生。在全咨模式下,咨询方根据业主委托提供设计、招标、造价、管理咨询等一体化服务,对建设项目全生命周期进行有机整合[1],可打破传统模式下参建单位间及专业间的信息壁垒,有效避免信息不对称现象发生,同时可综合考量项目全生命周期有关成本、进度、风险等有效信息,积极与业主、施工等参建方共享信息,利用共享信息的潜在价值降低项目成本、缩短施工周期、控制施工风险、促进项目效益最大化[2]。然而,全咨方不仅是业主委托的第三方机构,更是以盈利为目的的智力服务型企业,在一手掌握项目全生命周期重要信息,一手拥有各专业技术人才时,其是否能克服因信息不对称及自身优势而产生的机会主义行为,积极与参建方之间共享信息,帮助业主实现项目效益最大化是值得深究的问题。开展全咨模式下业主采取激励措施与咨询方积极共享信息之间的博弈行为研究,分析业主奖惩力度、咨询方共享信息成本与风险等因素对双方策略演化的影响,对于解决全咨项目信息不对称问题,促进全咨项目顺利实施具有重要的推动作用。
国内外已有大量学者采用博弈论研究建设项目主体之间的决策行为演化过程。对于参建方之间利益互动的研究,主要集中在实施绿色改造[3,4],开发绿色建筑[5~8],激发被动式建筑需求[9],规范招投标行为[10],业主与咨询方合作[11],制定合理碳税[12],发展装配式建筑[13]等方面。对于参建方之间信息共享的研究,Wang等[14]借助博弈论分析承包方、设计方和制造商的信息共享策略,并采用系统动力学得出演化规律;Hao等[15]建立建筑供应链博弈模型,发现奖惩力度、信任度与协同度可有效促进信息共享;闫文周等[16]从利益角度构建业主与参建方信息共享博弈模型,得出影响建筑供应链信息共享的关键因素;王莹[17]基于成本 - 收益角度建立开发商、制造商和承包商知识共享的SD-演化博弈模型;王德东等[18]采用博弈论分析业主与承包商共享信息的策略机制,确定了关键因素对双方行为的影响。
由以上分析可知,业内学者对于新兴全咨模式下参建方之间信息共享的研究鲜少。基于此,本文拟提出具有奖惩机制的演化博弈模型,以全咨模式下的业主与咨询方为研究对象,构建双方的激励机制 - 信息共享演化博弈模型,采用MATLAB 2016a对双方的演化博弈路径进行仿真模拟,分析影响业主采取激励措施与咨询方积极共享信息行为的关键因素。对于促进全咨模式下咨询方与业主等参建方之间信息共享,推动全咨模式的持续健康发展具有重要意义。
1 演化博弈模型构建
1.1 基本假设
在全咨模式下,业主扮演奖惩措施实施者和信息共享接收者,咨询方扮演共享信息主导者和奖惩措施接收者,基于业主与咨询方的激励机制 - 信息共享行为分析,影响双方选择积极行为的因素包括业主的激励水平、单方激励收益、激励成本、激励风险、投机收益、咨询方的信息共享水平、单方共享收益、共享成本、共享风险、投机收益等[19]。此外,业主可通过合同制定监管制度,安排工程进展计划,明确经济效益指标,并根据其他参建方反馈评估咨询方在信息共享方面的努力程度与投机行为,从而对其给予相应奖励与惩罚。因此,本文亦将业主的奖励与惩罚力度列为影响因素之一。通过构建全咨模式下双方的激励机制 - 信息共享动态演化博弈模型,分析影响因素对双方选择积极行为的作用效果,首先提出以下假设:
假设1:全咨模式下的激励机制 - 信息共享主体分为业主和咨询方,将业主设为A,咨询方设为B[11]。A作为委托方可选择是否对B进行额外奖励或惩罚,博弈行为策略集为{采取激励措施,未采取激励措施},故设A选择采取激励措施的概率为x(0≤x≤1),选择未采取激励措施的概率为1-x,即可涵盖A的所有行为选择;B作为信息不对称情况下占优势的一方,可选择是否付出额外努力共享信息,博弈行为策略集为{积极共享信息,未积极共享信息},同理,设B选择积极共享信息的概率为y(0≤y≤1),选择未积极共享信息的概率为1-y。
假设2:A未采取激励措施且B未积极共享信息时,A与B均依据合同指标执行常规工作,获得常规收益并承担常规成本,且A,B均未有额外收益与成本。故设A,B常规收益分别为N1,N2,常规成本分别为C1,C2[9]。由于A未采取激励措施,故不存在对B未积极共享信息的惩罚。
假设3:A单方采取激励措施而B未积极共享信息时,A因采取积极策略获得社会认可、市场资源等额外收益,承担人力、物力等成本与不利条件、经济损失等风险,且收益、成本和风险与A激励水平和对应系数有关,故设A激励水平为H1,单方收益系数为μ1,激励成本系数为ω1,激励风险系数为g1,惩罚系数为q,则A单方收益为μ1H1,激励成本为ω1H1,激励风险为g1H1,惩罚收益为qH2[20]。此时,B在A采取激励措施的情况下并未真正付出额外努力积极共享信息,从而获得有利条件、额外经济等投机收益,承担惩罚成本,且投机收益与A激励水平和投机收益系数有关,故设投机收益系数为α2,则B投机收益为α2H1,惩罚成本为qH2。
假设4:B单方积极共享信息而A未采取激励措施时,B因采取积极策略获得良好声誉、市场竞争力等额外收益,承担技术、经济等成本与经济损失等风险,且收益、成本和风险与B信息共享水平和对应系数有关,故设B信息共享水平为H2,单方收益系数为μ2,共享成本系数为ω2,共享风险系数为g2,则B单方收益为μ2H2,共享成本为ω2H2,共享风险为g2H2[15]。此时,A在B积极共享信息的情况下未对B做出的努力进行奖励,从而获得成本节约、项目效益提高等投机收益,且投机收益与B信息共享水平和投机收益系数有关,故设投机收益系数为α1,则A投机收益为α1H2。由于A未采取激励措施,故不存在对B积极共享信息的奖励。
假设5:A采取激励措施且B积极共享信息时,双方合作成本降低,协同努力提高项目的经济和社会效益,共同收益达到1+1>2的效果,从而获得协同收益并承担相应成本[16],且协同收益与A,B单方收益和协同收益系数有关,双方各自收益与分配系数有关。故设协同效益系数为β,A,B协同收益分配系数分别为n1,n2,则A,B协同收益分别为(μ1H1+μ2H2)βn1,(μ1H1+μ2H2)βn2,承担成本分别为ω1H1,ω2H2。由于A,B均采取积极策略,A对B进行奖励,且奖励与B信息共享水平和奖励系数有关,故设奖励系数为p,则A奖励成本为pH2,B奖励收益为pH2。
1.2 模型构建
由前述的基本假设,可得A与B的收益矩阵如表1所示。

表1 A与B的收益矩阵
1.3 复制动态方程及求解
在A与B的博弈过程中,收益较低的一方会通过调整自身策略来提高收益,这种动态调整机制可以采用复制动态方程来体现。
由收益矩阵可知,A采取激励措施的收益为:
U11=y[N1-C1+(μ1H1+μ2H2)βn1-
ω1H1-pH2]+(1-y)(N1-C1+
μ1H1-ω1H1-g1H1+qH2)
(1)
A未采取激励措施的收益为:
U12=y(N1-C1+α1H2)+(1-y)·
(N1-C1)
(2)
A的平均收益为:
(3)
A的复制动态方程为:

{y[(μ1H1+μ2H2)βn1+(g1-μ1)·
H1-(α1+p+q)H2]+(μ1-ω1-g1)H1+qH2}
(4)
同理可得B积极共享信息的收益为:
U21=x[N2-C2+(μ1H1+μ2H2)βn2-
ω2H2+pH2]+(1-x)(N2-C2+
μ2H2-ω2H2-g2H2)
(5)
B未积极共享信息的收益为:
U22=x(N2-C2+α2H1-qH2)+(1-x)·
(N2-C2)
(6)
B的平均收益为:
(7)
B的复制动态方程为:
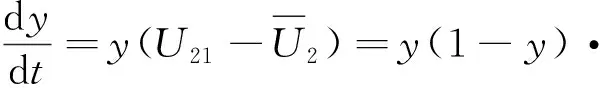
{x[(μ1H1+μ2H2)βn2+(g2-μ2+
p+q)H2-α2H1]+(μ2-ω2-
g2)H2}
(8)
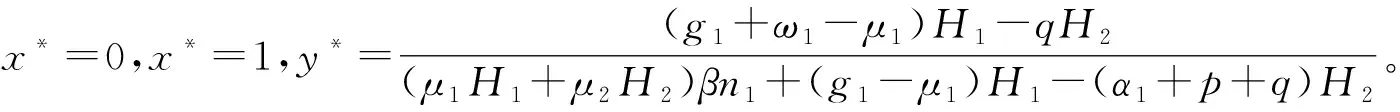
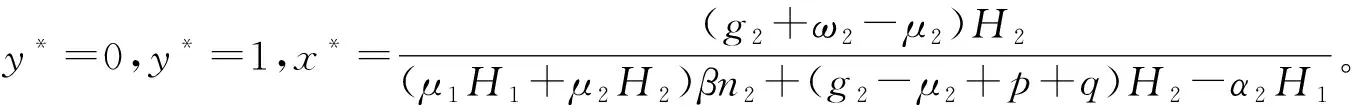
2 演化博弈模型分析
2.1 单方演化稳定策略分析
2.1.1 业主演化稳定策略分析
基于演化博弈稳定性定理,若使x*为演化稳定策略点,需要满足的两个条件为:F(x)=0且F′(x)=(1-2x){y[(μ1H1+μ2H2)βn1+(g1-μ1)H1-(α1+p+q)H2]+(μ1-ω1-g1)H1+qH2}<0。分情况讨论如下:
(1)当y=y*时,F′(x)≡0,故A的策略是稳定不变的。
(2)当y≠y*时,两个均衡点x*=0或x*=1均有可能成为演化稳定策略点:
1)当(g1+ω1-μ1)H1-qH2>(μ1H1+μ2H2)βn1+(g1-μ1)H1-(α1+p+q)H2时,F′(0)<0,F′(1)>0,故x*=0是演化稳定策略点;
2)当(g1+ω1-μ1)H1-qH2<(μ1H1+μ2H2)βn1+(g1-μ1)H1-(α1+p+q)H2时,若y
由以上分析可知,当(g1+ω1-μ1)H1-qH2>(μ1H1+μ2H2)βn1+(g1-μ1)H1-(α1+p+q)H2时,A的演化稳定策略是未采取激励措施;当(g1+ω1-μ1)H1-qH2<(μ1H1+μ2H2)βn1+(g1-μ1)H1-(α1+p+q)H2时,A是否采取激励措施与B积极共享信息的概率有关,若y
2.1.2 咨询方演化稳定策略分析
同理,若使y*为演化稳定策略点,需要满足的两个条件为:G(y)=0且G′(y)=(1-2y){x·[(μ1H1+μ2H2)βn2+(g2-μ2+p+q)H2-α2H1]+(μ2-ω2-g2)H2}<0。分情况讨论如下:
(1)当x=x*时,G′(y)≡0,故B的策略是稳定不变的。
(2)当x≠x*时,两个均衡点y*=0或y*=1均有可能成为演化稳定策略点:
1)当(g2+ω2-μ2)H2>(μ1H1+μ2H2)βn2+(g2-μ2+p+q)H2-α2H1时,G′(0)<0,G′(1)>0,故y*=0是演化稳定策略点;
2)当(g2+ω2-μ2)H2<(μ1H1+μ2H2)βn2+(g2-μ2+p+q)H2-α2H1时,若x
由以上分析可知,当(g2+ω2-μ2)H2>(μ1H1+μ2H2)βn2+(g2-μ2+p+q)H2-α2H1时,B的演化稳定策略是未积极共享信息;当(g2+ω2-μ2)H2<(μ1H1+μ2H2)βn2+(g2-μ2+p+q)H2-α2H1时,B是否积极共享信息与A采取激励措施的概率有关,若x
2.2 双方演化稳定策略分析
联立A,B的复制动态方程,可以得到5个系统局部均衡点:(0,0),(0,1),(1,0),(1,1),(x*,y*)。根据雅可比矩阵的局部稳定性对5个均衡点进行分析,当某一均衡点的雅克比矩阵满足行列式detJ>0且迹trJ<0时,表示该点能够达到局部渐进稳定状态,对应A与B的演化稳定策略(ESS)。
为分析雅可比矩阵行列式与迹的正负,定义如下6个多项式[21]:
①:(μ1H1+μ2H2)βn1-ω1H1-(α1+p)H2;
②:(μ1H1+μ2H2)βn2-α2H1+(p+q-ω2)H2;
③:(μ1-ω1-g1)H1+qH2;
④:(μ2-ω2-g2)H2;
⑤:(μ1H1+μ2H2)βn1+(g1-μ1)H1-(α1+p+q)H2;
⑥:(μ1H1+μ2H2)βn2-α2H1+(g2-μ2+p+q)·H2。
①与②分别表示A与B协同与投机收益之差。由于A,B均采取积极策略时会产生协同效益,从而使得A与B共同收益达到1+1>2的效果,所以可以判定①与②的值均大于0。
③与④分别表示A与B单方与常规收益之差。结合支付矩阵可以看出,尽管A,B单方采取积极策略时会获得额外收益,但还需承担额外成本与风险,当假设中所给系数没有确定时,无法判定③与④值的正负。
⑤=①-③,⑥=②-④,由于本文主要研究全咨模式下业主与咨询方的激励机制 - 信息共享行为,故可以假设当A采取激励措施且B积极共享信息时,A,B的协同收益足够大,使得⑤与⑥的值均大于0。
由于③与④的正负无法判断,需要分以下4种情形对演化路径进行分析:
(1)情形Ⅰ:①,②,③,④,⑤,⑥的值均大于0,即A,B的协同收益与单方收益大于常规收益。博弈出现一个不稳定点、两个鞍点、一个ESS点,双方策略演化结果为{采取激励措施,积极共享信息},演化博弈相位图见图1。

图1 情形Ⅰ演化相位图 图2 情形Ⅱ演化相位图
(2)情形Ⅱ:①,②,③,⑤,⑥的值大于0,④的值小于0,即A协同收益与单方收益大于常规收益,但B单方收益小于常规收益。博弈出现一个不稳定点、两个鞍点、一个ESS点,双方策略演化结果为{采取激励措施,积极共享信息},演化博弈相位图见图2。
(3)情形Ⅲ:①,②,④,⑤,⑥的值大于0,③的值小于0,即B协同收益与单方收益大于常规收益,但A单方收益小于常规收益。博弈出现一个不稳定点、两个鞍点、一个ESS点,双方策略演化结果为{采取激励措施,积极共享信息},演化博弈相位图见图3。
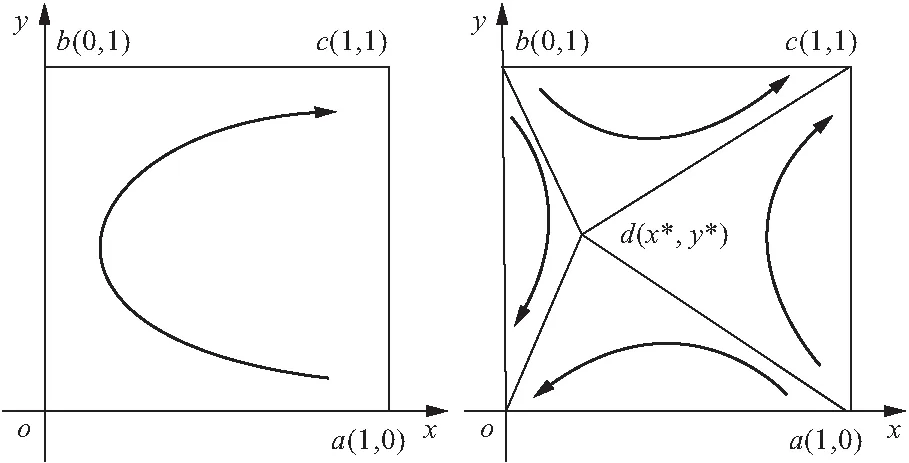
图3 情形Ⅲ演化相位图 图4 情形Ⅳ演化相位图
(4)情形Ⅳ:①,②,⑤,⑥的值大于0,③,④的值小于0,即A,B的单方收益小于常规收益。博弈出现两个不稳定点、一个鞍点、两个ESS点,双方策略演化结果为{采取激励措施,积极共享信息}或{未采取激励措施,未积极共享信息},即A与B要么均采取积极策略,要么均采取消极策略,演化博弈相位图见图4。
如图4所示,点d(x*,y*)为图中关键点,其与点a,b连成的折线为不同演化结果分界线,将图分为oadb与cadb两个区域。当A与B初始状态位于oadb区域时,双方演化结果为{未采取激励措施,未积极共享信息};当A与B初始状态位于cadb区域时,双方演化结果为{采取激励措施,积极共享信息}。不同演化结果与两个区域的面积有关,当oadb区域的面积越大,双方采取积极策略的概率就越小;当cadb区域的面积越大,双方采取积极策略的概率就越大。cadb区域的面积为:
(9)

表2 均衡点的稳定性分析
3 数值模拟与结果分析
针对情形Ⅳ,采用MATLAB 2016a对A和B的演化路径进行仿真模拟,定量分析各个参数对演化结果的影响,进而验证模型有效性。各个参数初始设定值见表3,初始值及变化值满足情形Ⅳ中所给条件。
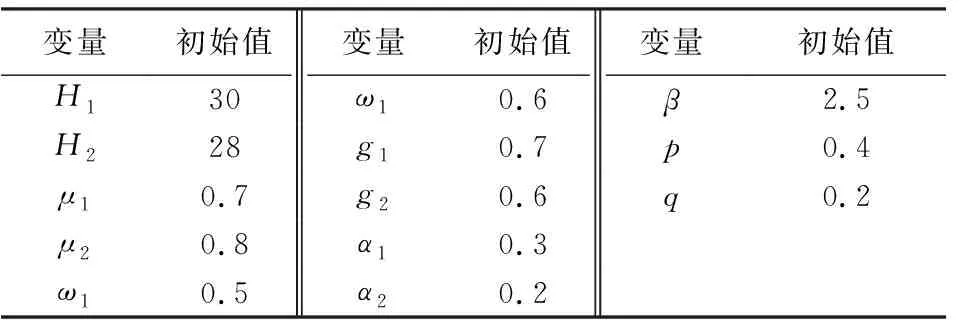
表3 参数初始设定值
(1)初始值状态下双方策略演化仿真分析。图5a为各个参数在初始值状态下,A,B采取积极策略的概率分别从0.1~0.9的演化结果。为更加清晰地反映双方策略的演化路径,图5b反映A,B均采取积极策略的初始概率分别为0.2,0.3,0.6与0.15,0.25,0.55时,双方策略选择随时间的变化情况。
(2)A激励水平调整仿真分析。保持其他参数不变,提高A激励水平得到图6所示演化结果。对比图5可知,当A与B选择积极策略的初始概率比较低时,即使A提高激励水平,但没有得到B正面反馈,使得更多演化过程趋向于(0,0),但当双方选择积极策略的概率比较高时,A提高激励水平加快演化过程向(1,1)的收敛速度。

图5 初始值状态下的仿真结果
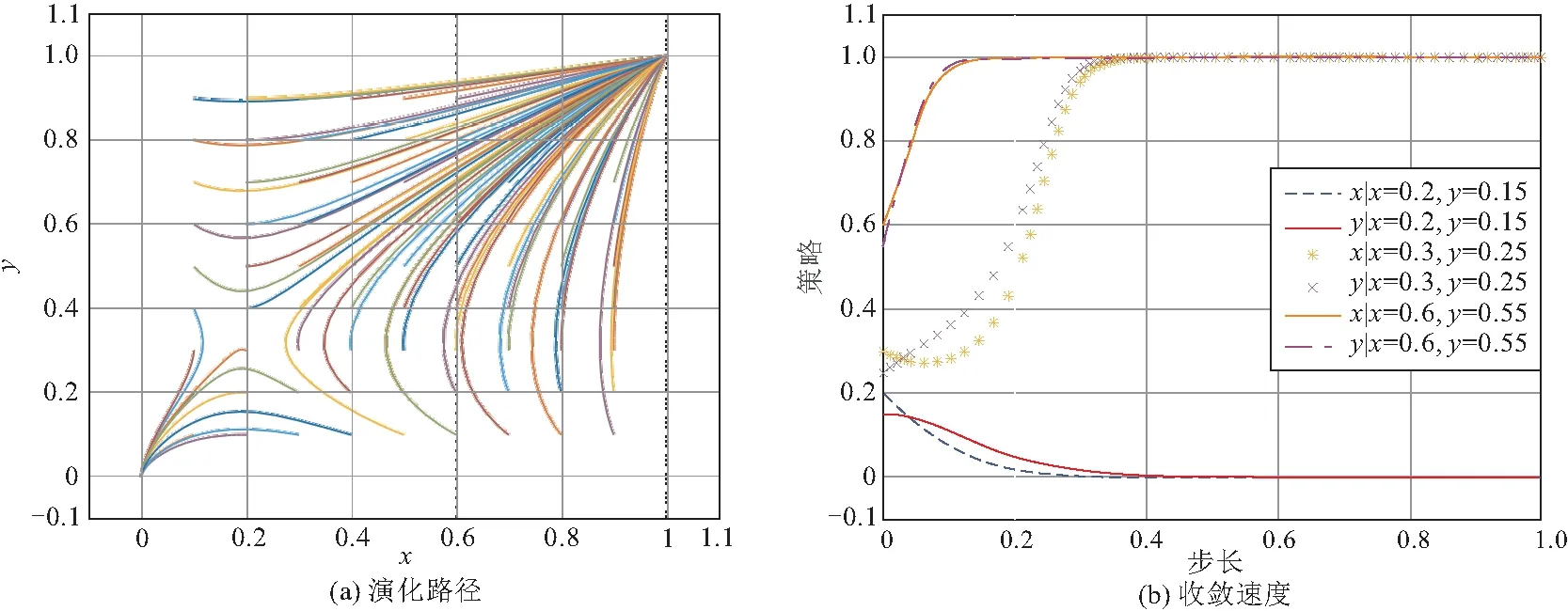
图6 提高A激励水平的仿真结果
由此可得,业主与咨询方选择积极策略的初始概率对双方的演化行为有一定影响,选择积极策略的初始概率越高,业主提高激励水平的效果就越好。业主可以通过给予精神与物质奖励促进咨询方利用自身专业知识积极共享信息,但应综合考虑咨询方共享信息的意愿,适时调整激励策略。当咨询方共享信息的积极性比较高时,业主可加大激励力度,促使经济效益成为咨询方积极共享信息的重要推动力,并形成共享信息的自觉行为,从而发挥激励措施的最佳效果。
(3)B信息共享水平调整仿真分析。保持其他参数不变,提高B信息共享水平得到图7所示演化结果。对比图5可知,B信息共享水平的提高使得趋向于(0,0)的演化过程明显减少,正向作用比较显著,同时在双方选择积极行为的初始概率相同时,减缓演化过程趋向于(0,0)的收敛速度,加快演化过程趋向于(1,1)的收敛速度,且双方选择积极行为的初始概率越高,收敛速度就越快。
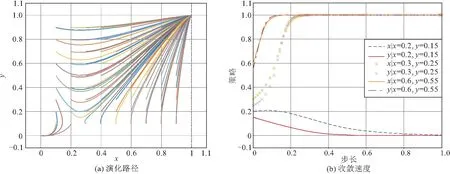
图7 提高B信息共享水平的仿真结果
由此可得,随着咨询方信息共享水平的提高,双方更倾向于选择积极策略。提高咨询方信息共享水平可有力推动双方合作共赢,这与闫文周[16]关于建筑供应链信息共享的研究结果不谋而合,且符合实际情况,在信息化时代,建筑项目信息的潜在价值被充分挖掘利用,信息共享水平将成为提高行业竞争力的重要条件。
(4)A与B单方采取积极策略收益系数、协同收益系数、奖惩系数调整仿真分析。保持其他参数不变,提高A与B单方采取积极策略收益系数得到图8所示演化结果。对比图5可知,提高单方采取积极策略的收益系数对A,B选择积极策略具有非常明显的正向作用,使得绝大多数演化过程都趋向于(1,1),同时加快了演化过程趋向于(1,1)的收敛速度,改变了x=0.2,y=0.15时的演化结果,使结果由趋向于(0,0)改变为趋向于(1,1)。协同收益系数与奖惩系数的提高对A与B采取积极策略都有着正向作用,且影响结果与提高单方采取积极策略的收益系数结果相似,按作用程度由大到小依次为双方单方采取积极策略的收益系数>协同收益系数>奖惩系数。

图8 提高A与B单方面采取积极策略收益系数的仿真结果
由此可得,单方收益是双方选择积极策略的关键因素。单方收益的增加不仅可以提高双方协同工作积极性,更可以在双方初始选择积极策略意愿并不明显的情况下,改善并促进双方达成良好的合作关系,张圣[11]在对业主与全咨方的博弈研究中亦印证了该点。此外双方均采取积极策略时附加的协同收益与业主制定合理的奖惩措施可进一步推进双方信任配合,激发合作积极性。
(5)A与B成本与风险系数调整仿真分析。保持其他参数不变,提高A与B成本系数得到图9所示演化结果。对比图5可知,双方成本系数的提高使趋向于(0,0)的演化过程明显增加,负面影响比较明显,同时在双方选择积极行为初始概率相同的情况下,减缓演化过程趋向于(1,1)的收敛速度,加快演化过程趋向于(0,0)的收敛速度,并且使x=0.3,y=0.25时的演化结果由趋向于(1,1)改变为趋向于(0,0)。风险系数的提高对A与B选择积极行为有着负面影响,且影响程度仅次于成本系数,此处不再过多赘述。

图9 提高A与B成本系数的仿真结果
由此可得,成本与风险系数提高会削弱双方选择积极行为的积极性,王莹[19]在研究业主与其他参建方信息共享行为时同样提到了成本与风险对双方策略的消极影响。无论业主还是咨询方,均希望减少不必要的成本支出和风险发生,以最小的成本与风险获得最大的收益,而这仅靠一方努力是不容易实现的,因而业主应给予咨询方足够的信任,咨询方应以优质的咨询服务回馈业主,从而使双方建立战略合作伙伴关系,以实现成本与风险的降低目标。
(6)A与B投机收益系数调整仿真分析。保持其他参数不变,提高A和B投机收益系数得到图10所示演化结果。对比图5可知,A和B投机收益系数的提高使得趋向于(0,0)的演化过程略微增加,存在微弱的负面影响,同时减缓x=0.3,y=0.25时演化结果趋向于(1,1)的收敛速度。
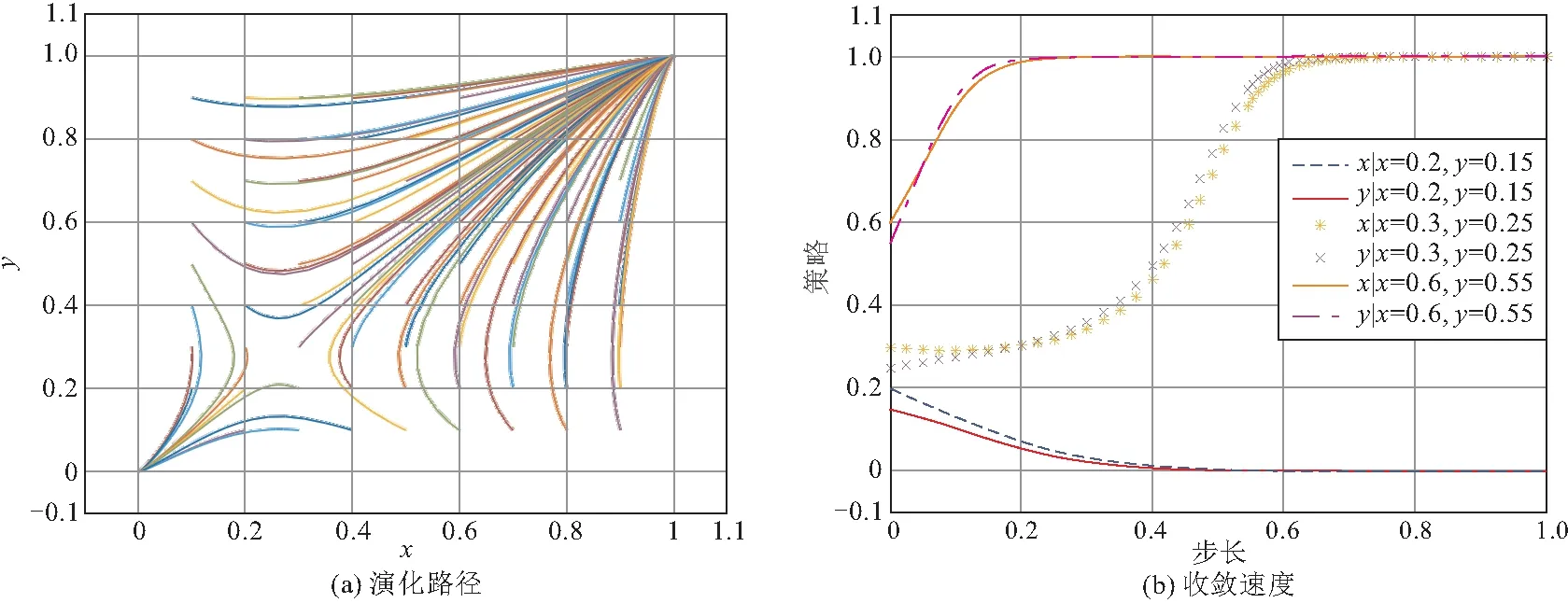
图10 提高A与B投机收益系数的仿真结果
由此可得,投机收益系数提高会对双方采取积极策略的意愿产生不利影响。作为追求利益最大化的团体,业主与咨询方均存在机会主义行为,尤其在全咨项目信息不对称的情况下,双方发生投机行为的倾向更加明显。但这是以牺牲长远发展谋求短暂利益的做法,不仅会破坏双方的信任合作关系,更会对其社会地位和公众形象造成不利影响,因而双方应规范自身行为,用长远目光看待自身发展,避免机会主义出现,以提高项目整体效益与双方共同利益为目标而努力。
4 结 语
通过构建全咨模式下业主与咨询方的激励机制 - 信息共享演化博弈模型,利用MATLAB 2016a对各个参数调整前后的演化路径进行仿真模拟,对比分析了影响业主采取激励措施与咨询方积极共享信息行为的重要因素以及作用程度。为促进全咨模式下咨询方与业主及参建方之间积极共享信息,利用信息创造项目价值,并与业主达成效益共享的友好合作关系,提出以下建议:
(1)咨询方在进行基础信息共享工作以外,应当积极引进信息技术人才,通过定期培训、内部交流等方式改善企业信息管理水平,提高共享信息能力。在工程建设过程中充分利用全过程优势,把握最能体现项目价值的设计阶段,利用BIM等信息技术挖掘信息价值,利用信息流改善物流和资金流,使资源得到合理分配,对项目进行统筹规划,进而帮助业主降低建设成本,缩短项目周期,减少工程变更,同时增强自身市场竞争力,赢得行业认可和长远发展。
(2)业主应根据建设成本减小额度,设置适当奖金激励咨询方充分利用信息价值优化工程建设效益,并设置适当惩罚额度对咨询方利用信息不对称优势谋取自身利益的投机行为进行惩罚。同时,在选择全咨企业时应充分了解其行业作风,慎重考虑激励条件,以免自身利益受到损害,当咨询方共享信息意愿明显时,业主可提出合适的激励条件促进咨询方利用自身专业技术与工程咨询经验提供优质的综合智力服务,加强双方相互信任,促进双方长久合作。
业主与咨询方应坚持资源共享、合作共赢的理念,以提高项目整体效益与双方共同利益为目标,达成激励机制 - 信息共享合作。但由于信息不对称,业主较难对咨询方在信息共享方面的努力程度与投机行为进行监管与评估,故实施奖惩措施时不确定性较大,该问题为今后提供了进一步的研究方向。

