基于动态安全距离的CACC车辆混合交通流模型
林 亨,方华建,吴冬雁
(1.温州大学 建筑工程学院,浙江 温州 325035;2.浙江浙峰工程咨询有限公司,杭州 310021)
21世纪,以车载路网传感器和道路辅助设施对周围交通环境数据实时交互技术为基础的新一代协同自适应巡航控制(Cooperative Adaptive Cruise Control,CACC)车辆成为当前车辆升级的主要趋势[1].相比传统车辆行驶中驾驶员判断延时、驾驶习惯和心理变化等差异,CACC车辆有望从微观车辆层面提升车辆驾驶过程中的稳定性,从而提高道路运输的效率并缓解交通拥堵的压力[2].基于此,开展CACC车辆混合交通流研究和相关参数设计,能推进车辆自动驾驶技术的发展和道路交通问题的改善.
当前,有关交通流理论的研究主要从宏观模型、介观模型和微观模型开展.其中,以元胞自动机模型为代表的微观模型是将道路离散为连续等间距的单元网格,结合一系列的演化规则进行车辆驾驶行为模拟.继经典的NaSch元胞自动机模型[3]再现了交通流中“时走时停波(Start-stop wave)”的特性后,不少学者在此演算规则上不断改进,提出了一系列改进的模型[4-7],极大程度上提升了交通流元胞自动机模型的适用性.其中,Bose等[8]提出自动-手动混合驾驶模型后,邱小平等[9]引入安全距离考虑混合交通流内车辆的安全驾驶行为.Yu等[10]结合数值拟算例分析指出,若CACC车辆考虑多辆前车间距能够改善行驶的稳定性.以上研究基于既定的车间距来处理混合交通流中车辆行驶关系,忽略了车辆行驶过程中的车间距的动态变化.
现有的研究已经表明,车头间距将影响车辆的行驶速度和刹车行为,从而对道路交通情况产生影响.在引入车间距与行车速度方程方面,Yan等[11]分析两车之间的最优速度差和电子节气门角度对车辆驾驶行为稳定性的影响.秦严严等[12-13]构造非线性期望车头间距-速度函数,分析不同比例CACC车辆跟驰模型混合交通流的行为差异,并以交通油耗为指标讨论了巡航控制系统的效果.曲昭伟等[14]改进最优速度(the Optional Velocity,OV)模型的固定安全距离的判据,提出得到更符合实际交通的理论模型.以上研究验证了行驶车辆间的车头间距对车辆驾驶速度变化的敏感性.同时,考虑驾驶员防御性驾驶心理因素,侯培国等[15]提出了急刹减速概率的混合交通流模型,模拟预测了实际交通中的“速度跃迁”的现象.张柠溪等[16]考虑相邻车辆的动态车间距,模拟出了驾驶员“高速跟驰”的车辆行驶习惯.相比而言,由于采用了驾驶辅助系统,CACC车辆可在驾驶环境和驾驶心理上做到更细微的控制,通过分析混合交通流的特性,为城市道路交通CACC车辆驾驶提供应对的策略和措施.
基于Gipps安全距离模型,本文引入动态安全距离来考虑CACC车辆与传统车辆的驾驶习惯和心理差异,提出了一种精细化的CACC车辆混合交通流数值仿真模型.通过将道路细化为一系列小尺寸网格,并结合元胞自动机模型的演化规则,对比车辆的时空演化图、流量-密度图等仿真结果,以分析不同反应时间下的CACC车辆比例和动态安全距离对道路交通流特性的影响.
1 模型建立
1.1 动态安全距离
在经典Gipps模型思想[17]中,安全距离Gapsafe,n是车辆为了避免与前车紧急刹车时发生追尾而必须保持的安全车间距.综合不同车辆属性和驾驶习惯,引入距离因子dn对传统安全距离Gapn的定义进行修正,如图1所示.图1中,ln为第n辆车的车身长度.假定t时刻前车n+1位于xn+1(t)处,速度为vn+1(t),此时后车n位于xn(t)处,其速度为vn(t).车辆n+1突然刹车至xn+1(t+1)停止,车辆n经过反应时间τn后速度变为vn(t+τn),然后再减速至停止xn(t+1)位置.由于存在驾驶习惯和驾驶心理的差异,与前车的间距考虑距离因子dn的影响.假定车辆是匀加减速运动,可得到动态安全距离的表达式为

图1 动态安全距离示意图Fig.1 Schematic diagram of dynamic safe distance

式中:bn为第n辆车的最大减速度.可见,其对应的动态安全距离Gapsafe,n受车辆行驶速度、反应时间和距离因子等变化的影响.
相比而言,CACC车辆能够借助车联网技术捕捉前车的行驶状态,其所对应的动态安全距离小,即时判断的反应时间τn快;而传统驾驶车辆因驾驶经验和心理变化的差异,需要较大的安全距离和判断时间[1].此外,出于行驶安全的需要,驾驶车辆在考虑距离因子的基础上保持与前车的距离满足以下条件

由此,求解一元二次方程可以得到对应车辆的行驶速度vn(t+τn)的表达式为

另一方面,当车辆处在自由流状态时,没有前车的干扰,Gipps模型[17]还对自由加速行驶的车速限定为
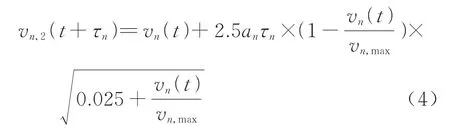
式中:an为车辆n最大加速度:vn,max为车辆最大行驶速 度.在 进 行 分 析 时,Gipps建 议 选 择min(vn,1,vn,2)进行车辆的速度更新.同时,与动态安全距离Gapsafe,n对应的行驶安全车速为vsafe,n.基于此,若设定车道上前,后车速度vn(t+τn)=vn+1(t)的关系,即车辆在反应时间能达到最大的车速为前车的速度,图2给出了不同车辆行驶速度、反应时间和距离因子情况下的动态安全距离Gapsafe,n.其中可以发现,车辆的行驶速度、反应时间、距离因子分别与车辆当前的动态安全距离成正相关.当加速度减小为0 m/s2时,不同车速情况下车辆的动态安全距离将退化为线性关系;而当加速度不为0 m/s2时,相同车速下距离因子越大的车辆所需的动态安全距离就越大,但这种效应随着反应时间的增加而有所降低.

图2 车辆速度、反应时间及距离因子与安全距离的关系Fig.2 Relationship between vehicle velocity,reaction time,distance requirement and safety distance

1.2 车辆驾驶模型
为精细化分析CACC车辆与传统车辆混合交通流的特性,将长度为L的单车道离散为尺寸长度为dL的一系列小元胞,则行驶车辆将占用离散道路多个元胞,如图3所示.同时,考虑该车道采用周期性边界条件,基于小尺寸网格的NaSch模型,分散的车辆在道路上根据以下过程进行演化:

图3 车辆占用离散道路示意图Fig.3 Schematic diagram of discrete lane occupied by vehicles
1)车辆状态分析.第n辆车前方的动态安全距离Gapsafe,n和行驶安全车速vsafe,n进行估算;
2)车辆加速规 则.当Gapn>Gapsafe,n时,则vn(t+1)→min{vn(t)+an,vn,max,vsafe,n(t),Gapn(t)};
3)车辆匀速规则.当Gapn=Gapsafe,n时,则vn(t+1)→min{vn(t),Gapn};
4)车辆减速规则.当Gapn<Gapsafe,n时,则vn(t+1)→max{min{vsafe,n(t),Gapn},0};
5)随机慢化概率.对于驾驶员在行驶过程中存在的驾驶行为的随机性,在演化规则中引入了随机慢化概率Rp,行驶中的车辆按照随机慢化概率进行速度上的慢化:vn(t+1)→max(vn(t+1)-bn,0);
6)车辆位置更新.在速度演化更新规则的基础上,进行车辆位置的更新:xn(t+1)→xn(t)+vn(t+1).
在仿真的模型中,当车辆比例r=1时,表示道路上全部的车辆均为CACC车辆模型;当r=0时,表示道路上全部的车辆为传统车辆驾驶模型;当0<r<1时,表示部分车辆为CACC车辆模型,其他为传统车辆驾驶模型.基于CACC模型和传统车辆模型具有不同的车辆反应时间τn和距离因子dn的前提,通过调整车辆比例r来分析混合交通流的特点.
2 仿真与数值模型
利用1.2节车辆演化规则进行数值仿真,本文设定整个车道的长度L为5 km,取小元胞单元尺寸dL和时间步长dt分别为0.5 m和1 s来细化整个车道.在仿真模型中,所有车辆的长度为7.5 m,每辆车占据15个元胞.考虑CACC车辆和传统驾驶车辆的最大车速vmax均取为135 km/h(对应数值模型中75个元胞单元),常规加速度an和减速度bn分别为3 m/s2(6个元胞单元)和3.5 m/s2(7个元胞单元),车道上车辆的速度就在0与最大速度之间取值,其中传统驾驶车辆的距离因子dn在0~1 m之间随机取值.按照不同车辆比例r,CACC车辆与传统驾驶车辆的初始位置和速度随机分布,则车道的平均流量J、车道的平均速度和车道总体车辆密度ρ为

式中:N是分布在车道上的车辆总数;vn(t)是第n辆车在t时刻的速度;T是所选样本的总时间长度;t0为所选样本开始计数的时间步.同时,前104时间步的数值结果不纳入统计计算以消除暂态影响.
2.1 车道流量和平均速度分析
对于自动驾驶的CACC车辆而言,其搭载的车载设备传感器能有效获取精准度高的前车信息,较大幅度地缩短自身车辆调整的反应时间[1].基于本文所提出的模型,取CACC车辆比例r范围为20%~100%,其中CACC车辆的反应时间τn,cc范围为0.2~1.2 s,传统车辆的反应时间τn,tc为1.5 s,得到不同反应时间车道混合交通流下的车辆密度-流量图和车辆密度-平均速度图,如图4所示.
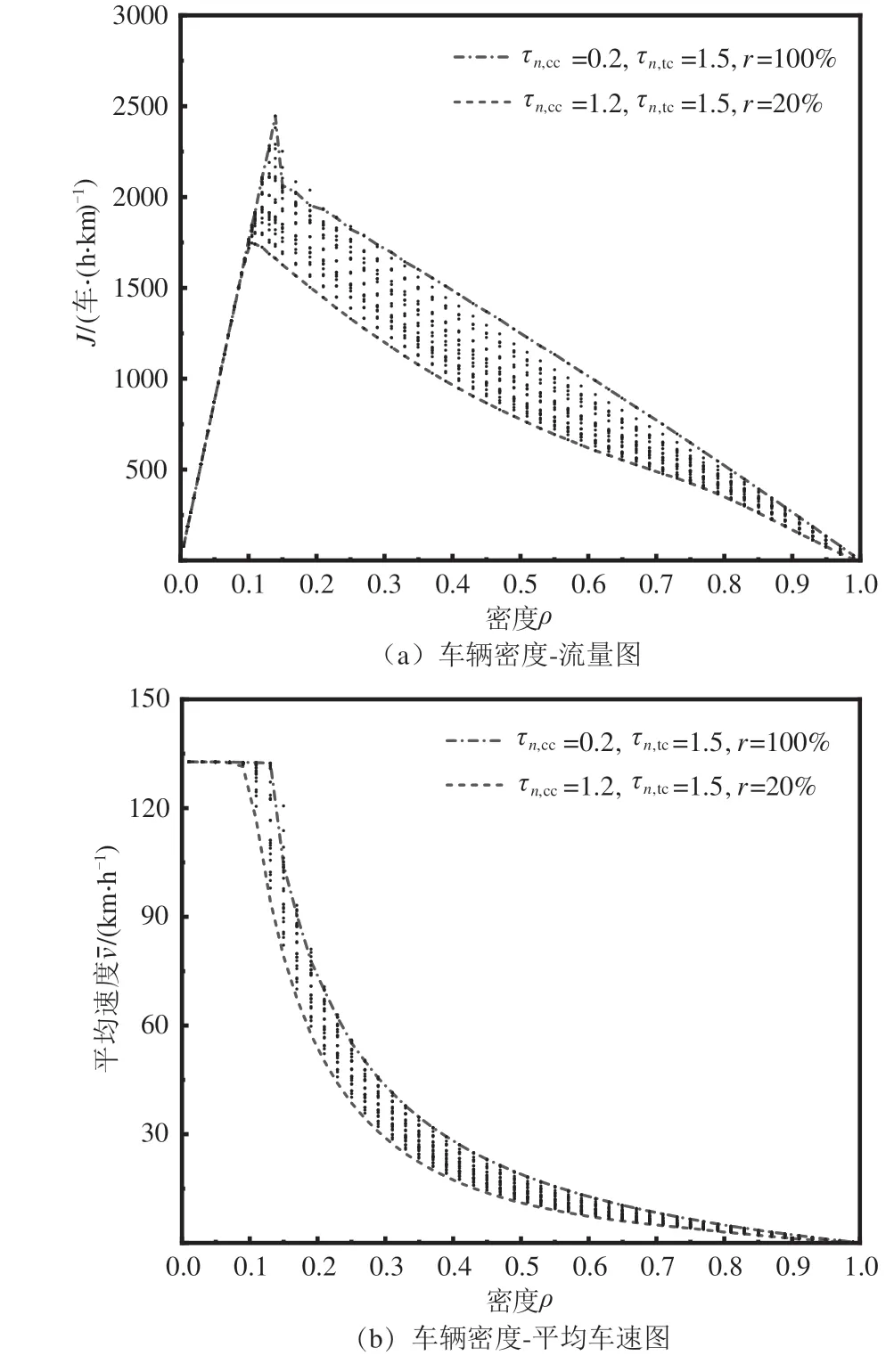
图4 不同反应时间的车道混合交通流基本图Fig.4 Basic diagram of mixed traffic flow on lanes with different reaction time
由图4(a)可知,在低密度的区域,流量与密度的关系近乎以直线相对应,但在中高密度区域,整个流量分布在二维的区域内,此与文献[18]提出的三相交通流理论较为符合.在低密度时,CACC车辆和传统车辆之间相互影响小,车速保持在最大车速的水准,车辆处在自由流的状态中,因此在低密度区,调整CACC车辆的反应时间或者车辆比例,其模拟得到的流量结果基本一致.但在中高密度时,CACC车辆的反应时间和车辆比例对流量产生明显的影响.结合动态安全间距的模型可知,由于CACC车辆比传统车辆所需要的反应时间短,使得车辆在行驶过程中所需要的动态安全间距要小,这确保了车辆能维持较快的行驶速度,从而改善车道的总体流量.相比而言,当车道车辆的反应时间趋于CACC车辆的反应时间时,其自由流过渡到拥挤流的临界密度增大,而当车道上车辆的反应时间增加时,车道流量“尖峰”现象就消失.
通过图4(b)不同反应时间的车辆密度-平均车速关系可以发现,当车道上的车辆处于自由流的情况下,车辆的平均速度基本保持不变,但当车辆密度增加时,车道总体的平均车速是逐渐减小的.对比发现,减小CACC车辆的反应时间或者增加CACC车辆的数量比例,对车道总体的平均速度是有提高的,但提高的幅度受到车辆密度的影响.总体上来说,平均速度大小反映出了车道流量的高低,所谓的车道流量“尖峰”现象的产生与车道总体较大的平均速度维持在较宽的车道密度范围内密切相关.
2.2 车辆运动微观分析
图5给出了车辆密度ρ为0.1、0.3以及CACC车辆反应时间τn,cc为0.2、1.0 s时,车 道 上CACC车 辆与其前车的速度和车间距的时间变化图,其中将精细化网格所对应的车辆速度和车间距统一单位为km/h和m.通过对比发现,安全车间距随着时间和前后车速度的改变而不断动态变化,由于车辆行驶的速度受到前后车的车间距制约,其速度变化要略滞后于其前车的速度变化.
分析图5(a)和图(c)可知,当车辆密度ρ为0.1时,CACC车辆与其前车的速度都处在较高的水平,其速度几乎都在100 km/h之上,这符合车辆密度-流量图中的自由流状态.此时,车辆之间的车间距动态波动幅度不大,车间距处在相对较大的水平,由于受到CACC车辆反应时间τn,cc的 影 响,当 车 辆 反应时间和车辆行驶速度越大时,对安全车间距的要求就越高,因此反应在车间距上的距离就越大.于此同时,对比图5(b)和图(d)的仿真结果发现,当车辆密度ρ增加到0.3时,前后车在车道上的行驶速度均有所下降,此时车道车流已经处于拥挤流的状态.由于受到车辆车速的影响,前后车的车间距因为车流中的阻塞而出现较大幅值的波动,这影响了车道中车辆行驶速度的稳定性.同样受到车辆反应时间的制约,车辆反应时间越慢,其车辆对于安全车间距的要求越高,但是考虑到此时行驶车辆的车速不大,故车间距的总体水平差异并不十分明显.通过对车辆运动的微观分析,基于动态安全距离的车辆模型能够反映出CACC车辆与传统车辆驾驶行为差异产生的影响,揭示了CACC车辆通过缩短车辆驾驶中的时间延迟来改善车道通行流量的内在机制.

图5 CACC车辆与前车速度及安全距离随时间的变化Fig.5 Time variations of velocity and safety distance between CACC vehicle and the preceding vehicle
3 车道拥堵分析
为了对混合交通流的动力学特征有更深入的理解,图6给出了不同车辆比例的车道车辆时空演化图.由图6可知,时空演化图中大多数车辆轨迹总体顺畅,局部存在长短不同波纹的情况,曾被研究者观察命名为“时走时停”波[3].而这种波纹也不同程度上反映出了车辆在道路上行驶的通畅程度.分析混合交通流的时空演化图发现,当r=20%~40%时,传统车辆的驾驶习惯趋同,这使得车辆保持基本上同步,而没有出现明显的阻塞情况;当车辆比例增加至60%时,CACC车辆与传统车辆对前车的反应时间差异使得阻塞波较多次出现在车辆行驶的轨迹中;但当车辆比例上升至80%时,原先打破的同步流再一次恢复,演化轨迹上的阻塞波明显减少.

图6 不同车辆比例下车道车辆的时空演化图Fig.6 Time-space diagram under different vehicle ratios
此外,文献[9]引入拥堵系数CR,通过清点整个车道车速小于10 km/h的车辆数目,计算其所占整个车道数量的占比来定量分析道路的拥堵情况.计算得到不同车辆比例下车道的拥堵比例系数为CRr,20%=7.58%,CRr,40%=6.20%,CRr,60%=4.82%,CRr,80%=2.50%,随着CACC车辆比例的增加,拥堵系数CR逐步减低,这说明CACC车辆通过缩短车辆驾驶的反应时间延迟将对道路交通产生积极的影响.图7进一步给出不同车辆反应时间和CACC车辆比例情况下的拥堵系数示意图.基于数值仿真的模型结果,车辆密度大的拥堵系数要远大于车辆密度小的拥堵系数,车辆密度是决定道路拥堵的绝对因素.在此基础上进行数据分析,无论车道上车辆密度如何变化,在CACC车辆比例低的范围内,拥堵系数CR均处在较高的水平,但随着车辆比例的逐步提升,拥堵系数开始逐步下降,但下降的速率受车辆反应时间大小的影响.在动态安全距离的模型中,车辆跟驰的动态安全间距受到车速和反应时间的双重制衡,因此在低车辆密度和高车辆比情况下的拥堵系数指标出现非均匀性的分布特征.
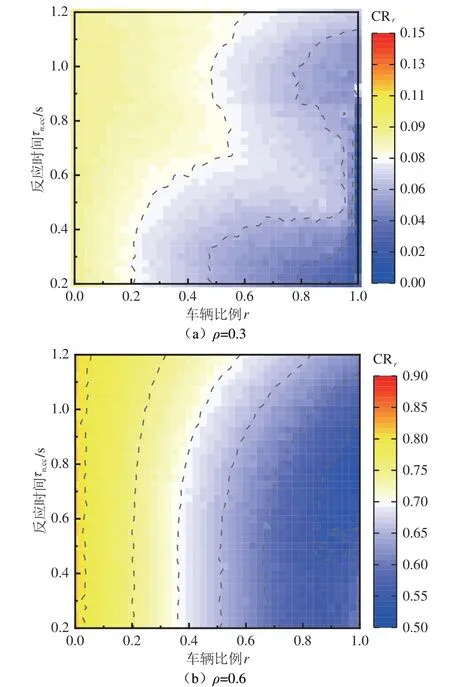
图7 不同车辆反应时间和车辆比例情况下的拥堵系数分布Fig.7 Traffic congestion index distribution under different vehicle ratios and reaction time
4 结论
1)考虑驾驶条件和驾驶心理的差异构建动态安全间距,其随着车辆车速的增加和反应时间的延迟将呈现非线性的改变,并且考虑动态安全距离的车道混合交通流基本图符合三相交通流理论的基本特征.
2)在相同的车辆密度下,提高CACC车辆的比例和减小车辆的反应时间能够提高车道车辆的平均速度和整体的车道流量.基于CACC车辆搭载车载设备获取较精准的前车信息,在车辆驾驶过程中可预判前车的驾驶行为而采取不同的跟驰速度.
3)车道的拥堵系数CR随着CACC车辆比例的上升而减低,其效果随着车辆反应时间的增加而逐步减低,但其影响在车辆拥挤密度大的情况下更为明显.

