降雨型大孔隙斜坡非平衡流与失稳特性试验研究
李尚辉,阙 云,詹小军
(1. 重庆交通大学 土木工程学院,重庆 400074; 2. 福州大学 土木工程学院,福建 福州 350108)
0 引 言
滑坡灾害是自然界最普遍的地质灾害之一,而降雨是引发滑坡灾害的主要原因[1-2]。基于饱和/非饱和渗流理论的研究表明[3-5],降雨导致土体基质吸力降低、土体软化、坡面受冲刷和地下水位发生改变,从而诱发滑坡。但是,土体是一种复杂的多孔介质,其结构与成分丰富多彩,在降雨作用下,不同土质中水分运移机理表现出较强的各异性。
花岗岩残积土孔隙比大,是一种典型的大孔隙材料[6-8],降雨作用下水分优先流经大孔隙域并迅速抵达土体深部,从而产生非平衡流[9-11]。虽然单位土体中大孔隙域占比非常小(0.1%~5.0%),但依然会导致水分及相关溶质在土中产生非平衡流现象[12]。非平衡流条件下土体水分的运移速度远大于达西定律描述下的运动特性,单一的达西定律无法对此准确描述[9]。可见,对含大孔隙斜坡中水分运移机理的研究应结合非饱和非平衡流的理论来实现。
SHAO Wei等[13-14]利用有限元模拟研究了传统非饱和渗流与含大孔隙斜坡的边坡稳定性,分析了非平衡流对快速压力响应和滑坡触发的影响;阙云等[15]建立了非平衡流模型,通过有限元分析,揭示了短时冻区冰雪消融对残积土坡稳定性的影响。虽然截至目前关于非平衡流的研究取得了一些进展,但主要偏向于土壤学科,且比较重视溶质运移等较为单一的渗流形式[16-17],也未充分考虑土水特征曲线的空间变化特征[18-20],而对岩土工程学科中大孔隙斜坡降雨入渗与稳定性试验研究仍显不足。
笔者以福建省某高速公路残积土斜坡为例,建立了缩尺大孔隙斜坡模型,通过室内试验监测30 mm/h和80 mm/h两种降雨强度下土体体积含水率、竖向位移、孔隙水压力、土压力、坡面流速和径流量等指标,分析了降雨作用下大孔隙斜坡非平衡流与失稳特性。研究结果可为含大孔隙公路路基边坡灾害防治提供参考。
1 边坡模型相似比与相似材料
福建省每年3—9月降雨量十分充沛,全省山地丘陵花岗岩残积土厚、孔隙率大,大孔隙比例可达2.40%~48.72%[7],降雨作用下水分运移的非平衡流特性显著。笔者以厦蓉高速公路福建段路堤边坡为模拟试验对象开展研究,为了使试验用土性质与原始边坡土体性质尽可能一致,首先通过相似比关系来确定试验用土的黏聚力c、内摩擦角φ、压缩模量E、渗透系数K等参数,见表1。
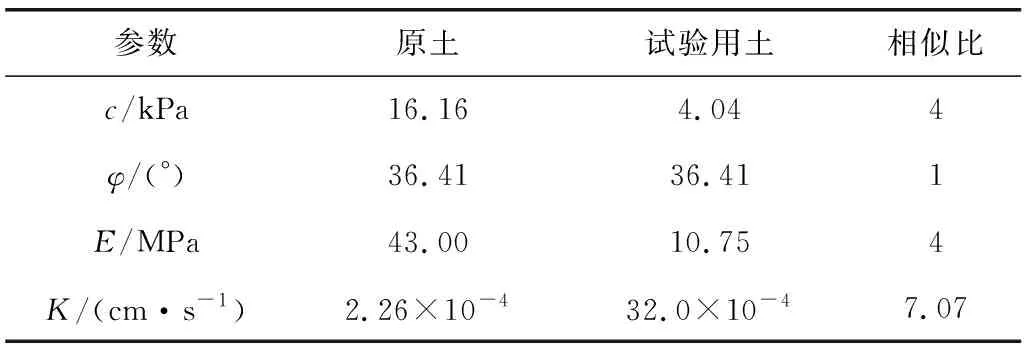
表1 模型材料相似比参数Table 1 Model material similarity ratio parameter
为了配制出符合表1参数的试验用土,在原土中添加重晶石粉、石英砂及水、液态石蜡,通过正交试验确定出模型材料配比:m原土∶m重晶石粉∶m石英砂=20%∶60%∶20%,m水∶m液态石蜡=64%∶36%。
2 试 验
2.1 边坡模型设计
试验边坡模型缩尺比例为1∶50;模型长160 cm,高60 cm;坡顶长50 cm,坡趾长46 cm;分2级放坡,坡比均为1∶1.5。详见图1。

图1 边坡模型几何尺寸(单位:cm)Fig. 1 Geometric dimensions of slope model
2.2 大孔隙布置
首先,在土体内部埋入一根直径为2 cm的不锈钢钢管并封闭管口,边坡填筑完成后向其中灌入粗石英砂;然后,采用螺旋上升方式缓慢拔出钢管,从而形成近似的大孔隙通道。
在边坡模型中共布置了30个大孔隙通道。沿着长边设置10排,沿着短边设置3排;大孔隙均匀分布在坡顶、坡中和坡脚处;所有大孔隙通道上部连通;坡脚处大孔隙通道长度20 cm,其他位置30 cm。详见图2。

图2 大孔隙布置(单位:cm)Fig. 2 Macropore detailed layout
2.3 试验装置
2.3.1 降雨系统
1)供水箱,为降雨过程持续供水。
2)水泵,是降雨的主要动力来源,水泵压力可以根据需要进行调整。
3)降雨装置,包括水管支架及喷头等,降雨高度为6 m,降雨有效面积为12 m2,支架布置与喷头协调。喷水点共计6个,间距为2 m,喷口直径大小可适时调整以模拟各种不同降雨强度。
4)雨量筒,用于监测降雨过程中实时雨强变化情况。
2.3.2 监测装置
1)土体体积含水率θ采用TDR-3型土体水分传感器来监测。
2)坡顶和坡中台阶处竖向位移u采用位移计来监测,其固定如图3。
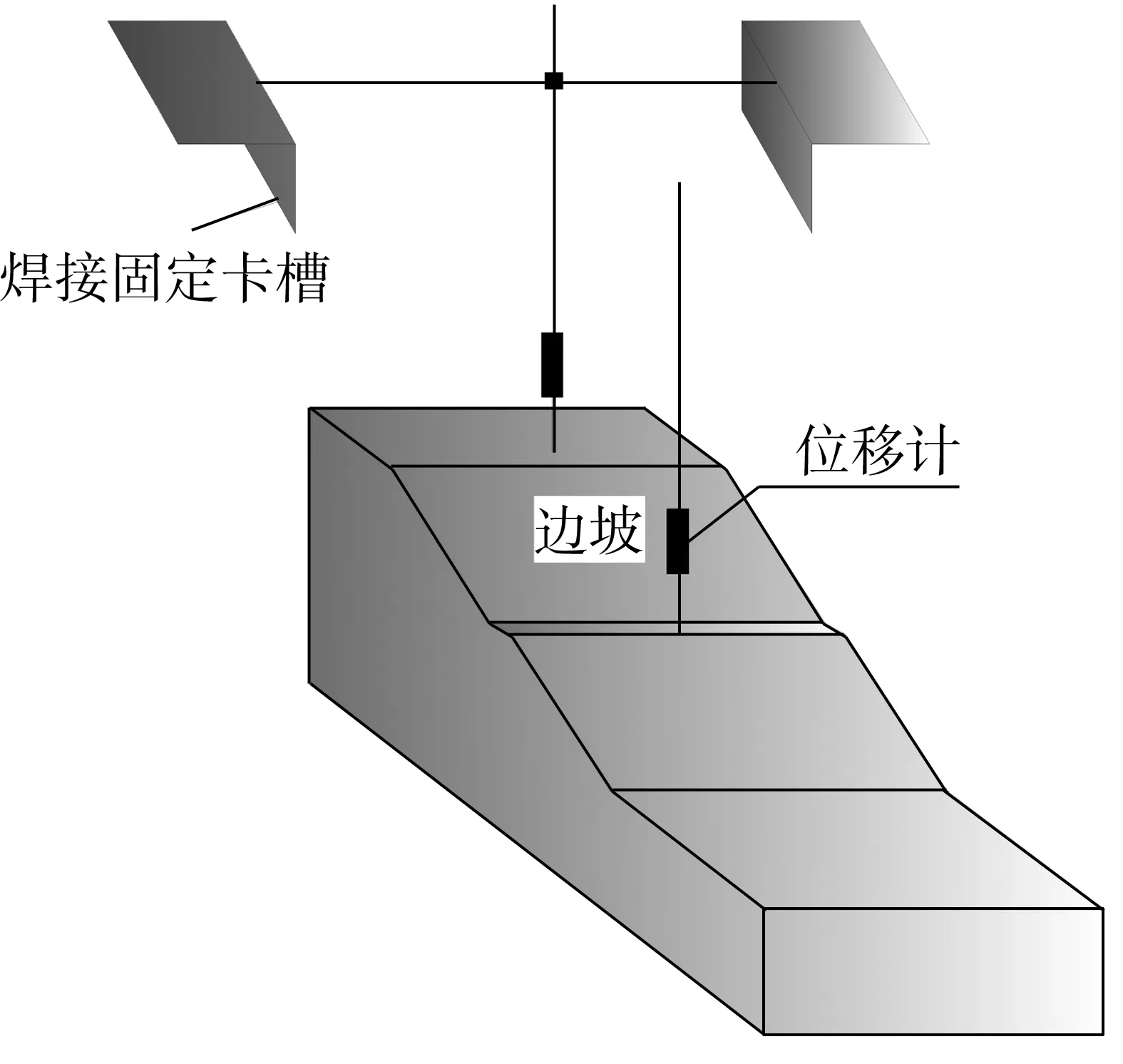
图3 位移计固定示意Fig. 3 Schematic diagram of displacement meter
3)边坡失稳时的位移采用PhotoInfor图像处理软件采集。
4)孔隙水压力p采用CYY2应变式孔压计结合UT7110型数据采集系统来监测。
5)土压力σ采用LCTY-1型土压力盒监测。
6)坡面径流用自行设计的三角玻璃引流槽来收集,坡面径流流速v用染色剂法测定[21]。
2.3.3 监测装置布置
在定制的亚克力有机玻璃模型箱〔图4(a)〕中填筑试验边坡土体,同时将角钢支架焊接在模型箱外围以确保模型箱牢固,为了便于收集坡面径流量,模型箱侧面预留40 cm × 2 cm的方形孔。亚克力模型箱侧面预留10个水分传感器孔洞,由坡脚至坡顶编号1 #~10 #,孔洞水平间距15 cm,竖向距离坡顶分别为8、20、30 cm,2 #、4 #、8 #、9 #孔洞距离坡面8 cm。除了坡顶第1、2排孔洞间距为12 cm之外,其余第2、3排和第3、4排孔洞竖向间距均为10 cm。

图4 监测装置布置(单位:cm)Fig. 4 Monitoring instrument layout
试验开始之前将对应编号的水分传感器通过孔洞插入土体用于监测土体体积含水率θ。
孔隙水压力监测点布置4个,竖直位置分别位于1 #、4 #、7 #、8 #孔洞处;土压力监测点布置2个,竖直位置分别位于2 #、7 #孔洞处,位移监测点布置2个,分别位于坡顶和坡中台阶处。
2.4 试验流程
边坡降雨试验流程为:开始→检查调试降雨系统→配置试验用土→绘制边坡土层填筑线→降雨均匀度测试→边坡填筑与布设TDR、孔压计等仪器→架设相机与水槽→降雨试验开始→试验数据采集→清理试验场地→结束。
3 结果分析
3.1 土体体积含水率θ
图5为降雨强度R=30、80 mm/h时,边坡不同位置监测点土体体积含水率θ随时间t变化曲线。

图5 R=30、80 mm/h,各测点的θ-t曲线Fig. 5 Curves of θ-t at each monitoring point when R=30, 80 mm/h
由图5可见:
1)降雨强度R=30 mm/h时。各监测点θ随t的变化趋势基本一致,即t=0~50 min时,θ保持初始值不变,大约为10%;t> 50 min,θ逐渐增大;t≈250 min时,θ趋于稳定,大约为30%。埋深较浅的1 #、2 #、4 #、8 #、9 #监测点,θ响应时间为50~75 min;埋深较深的3 #、5 #、6 #、7 #、10 #监测点,θ响应时间约为200 min。表明在降雨作用下,离坡面越近,土体体积含水率变化越敏感。各监测点土体体积含水率饱和峰值θpeak=28%~32%。
2)降雨强度R=80 mm/h时。各监测点θ变化趋势与R=30 mm/h时相似,但不同监测点θ响应时间的滞后不同,大部分集中在25~50 min时段,最终,各监测点土体体积含水率饱和峰值θpeak≈ 33%,比R=30 mm/h时大。表明增大降雨强度可使得土体体积含水率响应时间提前,增长速率变快,非平衡流现象更显著。
3.2 孔隙水压力p
图6为降雨强度R=30、80 mm/h时,边坡坡脚、坡中及坡顶处孔隙水压力p随时间t变化曲线。

图6 R=30、80 mm/h的p-t曲线Fig. 6 Curves of p-t when R=30, 80 mm/h
由图6可见:
1)R=30 mm/h时,经过一定时间后,各监测点p由0开始迅速增大,其中1 #、8 #监测点p响应时间最早,大约为40 min,4 #监测点响应时间其次,7 #监测点响应时间最迟,大约为150 min。最终,1 #、4 #监测点p趋于稳定的峰值,而7 #、8 #监测点p达到峰值后逐渐减小,其中8 #监测点在150~250 min阶段p逐渐减小,降雨至250 min后减小到0。分析原因是:降雨时间足够长时,坡面径流导致坡顶形成冲蚀沟,p降低过程说明孔压计处于部分裸露状态;若p减小至0,说明孔压计已经处于完全裸露状态。
2)R=80 mm/h时,各监测点p响应时间相比R=30 mm/h时显著提前,1 #监测点响应时间提前至10 min,7 #提前至40 min左右。说明R越大,响应时间滞后性越小。1 #监测点保持p≈0.5 kPa,直至t=100 min后继续增大,最终ppeak≈1.0 kPa,这是由于坡脚积水导致p出现二次增大。
3)7 #、8 #监测点p开始减小的时间大幅提前。最终,7 # 监测点p在150 min左右维持在1.0 kPa左右,此时8 #监测点p已经减小到0。表明降雨强度越大,坡面越容易产生坡面径流。
3.3 土压力σ
图7是降雨强度R=30、80 mm/h时,2 #、7 #监测点土压力σ随时间t变化曲线。

图7 R=30、80 mm/h的σ-t曲线Fig. 7 Curves of σ-t when R=30, 80 mm/h
由图7可见:
1)R=30 mm/h时,2 #、7 #监测点σ先增加后缓慢减小,当t< 120 min时,两者增长速率相当;当t>120 min时,7 #监测点的σ增长速率显著大于2 #监测点的;当t≈300 min时,2 # 监测点的σ出现突降。分析原因,主要是坡脚处发生局部垮塌破坏导致压力释放。
2)R=80 mm/h时,降雨开始阶段,7 #监测点的σ增长速率显著大于2 #监测点的,两者达到峰值对应的时间分别是160 min和190 min,即7 # 监测点的σ率先达到峰值。分析原因是,坡面出现积水流入大孔隙,且流入7 # 监测点的积水早于2 # 监测点的,流入7 #监测点的水分也更多。与R=30 mm/h时相比,R=80 mm/h时,2 #、7 #监测点的土压力峰值σpeak分别增长了约211%、176%。7 #监测点位于坡顶,由于坡顶径流形成冲蚀沟,σ最终减小至5.3 kPa,降雨后期临近坡脚发生失稳破坏使得2 #监测点σ最终减小至4.8 kPa。
3.4 竖向位移u
图8为降雨强度R=30、80 mm/h时,坡顶和台阶处竖向位移u随时间t变化曲线。

图8 R=30、80 mm/h时,坡顶和台阶处的 u-t曲线Fig. 8 Curves of u-t at the top and step of slope when R=30, 80 mm/h
由图8可见:
1)R=30 mm/h时,坡顶和台阶处u随着t的增大而增大,且坡顶处的增长幅度比台阶处的大。当t≈325 min时,由于出现局部垮塌破坏,坡顶处u骤增,短时间内由76 mm增至90 mm;当t≈375 min时,台阶处u出现相同变化,从45 mm迅速增至66 mm。
2)R=80 mm/h时,同样,坡顶和台阶处u先逐渐增大,随着局部垮塌而突变,最终达到极值;但与R=30 mm/h时相比,u发生突变的时间大大提前。表明:降雨作用下,大孔隙边坡坡顶处的u比台阶处的大,坡顶更容易发生局部垮塌破坏。
3.5 坡面流速v与坡面累计径流量q
图9分别为降雨强度R=30、80 mm/h时,坡面流速v与坡面累计径流量q在降雨历时220 min内的变化曲线。

图9 R=30、80 mm/h,q-t、v-t曲线Fig. 9 Curves of q-t and v-t when R=30, 80 mm/h
由图9可见:
1)当R=30 mm/h时:①坡面径流产生,累计径流量q随时间t的增长逐渐增大,t<120 min时,q较小;当t≥120 min时,q迅速增长;当t≈220 min时,q达到11 000 g。②径流初期,坡面流速v迅速增大,t=18 min后增速放缓,在75 min~120 min阶段,v的变化出现一定的波动,最终稳定在v=0.010 5 m/s左右。
2)当R=80 mm/h时:①t< 75 min,q增长速率较慢;t=75→220 min,q=6 000→50 000 g。②t=0→60 min,坡面流速v=0→0.045 m/s,最终,稳定波动于v=0.039 m/s。
综上,坡面累计径流量q和坡面流速v均随降雨强度R的增大而增大。分析原因是,增大降雨强度使得大孔隙域能够在更短的时间达到饱和状态,水分入渗至大孔隙域的阻力增大,致使坡面累计径流量变大。
3.6 边坡破坏过程
图10为降雨强度R=30、80 mm/h时,PhotoInfor图像处理软件识别的不同降雨时刻土体位移云图。
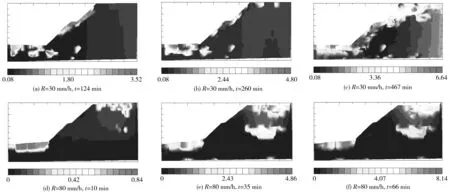
图10 R=30、80 mm/h,不同降雨时刻土体位移云图(单位:cm)Fig. 10 Soil displacement nephogram at different rainfall moments when R=30, 80 mm/h
由图10可见:
1)R=30 mm/h,非平衡流作用下,t=124 min时,台阶处位移达3.52 cm;t=260 min时,整个坡面位移均发生较大变化,位移最大为4.80 cm;t=467 min时,边坡出现大规模破坏,最大位移发生在坡顶处,达到6.64 cm。对试验边坡的观察发现,09:40—17:30持续降雨后,边坡出现大规模破坏。
2)R=80 mm/h,t=10 min时,坡顶表面及其下覆一定深度土层位移均发生变化,最大值为0.84 cm;t=35 min时,位移发生变化的范围增大,最大值达4.86 cm;t=66 min时,坡顶最大位移进一步增加到8.14 cm。对试验边坡的观察发现,10:00—14:45持续降雨后,边坡出现大规模破坏。
综上,与R=30 mm/h相比,R=80 mm/h时竖向位移在短时间内即发生大幅度变化。分析原因是,较大降雨强度下,受大孔隙流冲蚀作用,基质域土体压实度降低。
根据降雨过程中位移变化情况和边坡完整度的观察,将边坡的破坏形式分为初始破坏和最终破坏,初始破坏以出现首块可见滑体或出现首个冲蚀沟为依据,最终破坏以出现大规模滑体为依据,破坏实况如图11。

图11 R=30、80 mm/h,不同降雨时刻边坡破坏形式Fig. 11 The failure form of slope at different rainfall moments when R=30, 80 mm/h
由图11可见:
1)R=30 mm/h时,坡面发生初始破坏的时间为 285 min,此时坡面出现沉降裂缝,随着降雨的进行,雨水不断浸润,坡面由于重力作用产生拉裂缝;在降雨时间达到 470 min时,坡面发生最终破坏,此时坡顶和斜坡界面均产生滑移裂缝,边坡破坏形式为浅层局部滑裂破坏。
2)R=80 mm/h时,坡面发生初始破坏和最终破坏的时间分别为20 min、285 min;发生最终破坏时,坡面未出现裂缝,但由于降雨强度过大和较大的竖向位移,坡面产生冲刷作用,边坡破坏形式为浅层局部冲刷破坏。
综上,R=80 mm/h时,边坡发生初始破坏时间和最终破坏时间较R=30 mm/h时分别提早了265 min和185 min,破坏程度更大,至降雨停止时,坡体近乎冲刷流失。因此,降雨强度越大,边坡破坏速度越快,边坡的破坏形式也发生较大变化。
4 结 语
1)同一降雨强度下,监测点埋深越浅,体积含水率响应时间更早。随着降雨强度增大,不同监测点体积含水率响应时间滞后特性减小,体积含水率增长速率增大,非平衡流现象愈加显著。
2)降雨强度越大,孔隙水压力响应时间越早,坡脚处更容易出现积水,由此导致坡脚处孔隙水压力出现二次增大。此外,增大降雨强度,坡顶处冲蚀沟形成时间提前,坡顶卸压时间相应提前。
3)随着降雨进行,坡脚和坡顶处土压力先增加后缓慢减小,且坡顶处土压力增幅较坡脚大,坡脚土压力达到峰值时间滞后于坡顶。随着降雨强度增大,坡脚和坡顶土压力峰值也越大。
4)降雨初期,坡顶和台阶处竖向位移缓慢增大,当发生局部垮塌时,竖向位移骤增至峰值并保持不变。坡顶处位移增长速率相比台阶更大,局部垮塌点出现时间更早,大孔隙边坡坡顶相比台阶更容易发生破坏。
5)降雨强度越大,坡面累计径流量进入快速增长阶段越早,坡面累计径流量达到的峰值越大;降雨强度越大,坡面流速进入波动界限范围越快,流速峰值也越大。
6)随着降雨强度增大,边坡初始破坏和最终破坏时间提前。不同降雨强度下,大孔隙边坡最终破坏形式不完全相同,降雨强度较小时,以浅层局部滑裂破坏为主;降雨强度较大时,以浅层局部冲刷破坏为主。
7)通过与过去普通边坡大量的研究成果对比,考虑大孔隙情况下,边坡非平衡流特性更加明显,渗流场响应时间更早,响应速度更快。大孔隙在一定程度上会提高边坡垮塌破坏的几率,使得滑坡时间提前。

