Scratch矢量动画基础

任亚飞

为了使用Scratch绘制立体图形，我们需要具备一些向量和三角函数的基础知识，通过让图形移动和缩放我们可以更好地掌握这些知识。

一、点与向量

点：数学概念点是最简单的图形，在Scratch中用平面直角坐标系定位。

向量：具有大小和方向的量就叫向量，用于描述事物去哪里。

表现为箭头，尖端为向量头，另一端为向量尾。在字母上加箭头表示，如V。向量可以执行加减法和乘法运算。

向量加法：向量的加法用平行四边形法则和三角形法则。新向量表示为a和b的起点重合后，以它们为邻边构成的平行四边形的一条对角线或者表示为将a的终点和b的起点重合后，从a的起点指向b的终点的向量。

向量减法：向量a和b的相减，可以看成是a向量加上一个与b大小相等，方向相反的向量。表示为a和b的起点重合后，从b的终点指向a的终点的向量（图1）。

列向量：坐标系中的向量可以用它们的x分量和y分量来表示，这叫列向量表示法。而且向量不需要停留在原点，可以放置在任何地方（图2）。

乘法：标量k和向量之间可以做乘法，结果是另一个与方向相同或相反的｜k｜倍的向量（图3）。

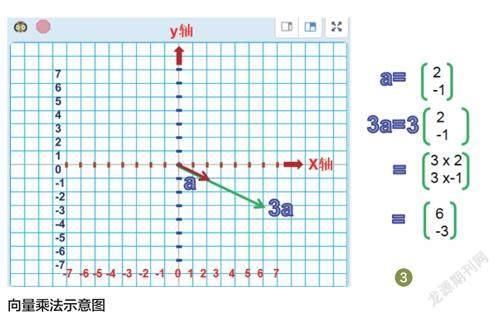
二、线段

直线上两点间的部分就是线段，刚才在Scratch中就是画笔从坐标（0，0）落笔到（5，3）抬笔。

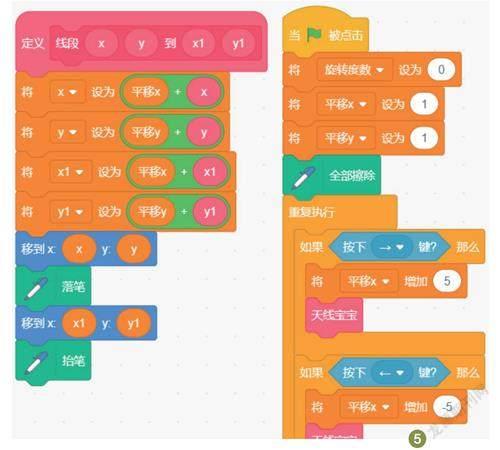
我们用线段画出一个小电视。封装两个自定义函数积木。一个线段函数积木，画出两个坐标值间的线段。通过4个变量来控制坐标，其中x和y变量是起始坐标向量尾，x1和y1是向量头。另一个函数积木是用线段画小电视，具体取值见图4。

三、移动

通过觀察发现，小电视左右移动是平移X轴，y轴无变化。只需要对向量头和尾的X轴的标量加减运算，也就是改变x轴坐标值。上下移动则只改变y轴坐标值。通过新建变量“平移x”和“平移y”与函数积木线段对应的参数运算后就可以实现小电视的上下左右移动（注：我们每改变一次x、y轴的量，函数线段和函数小电视就会重新执行一遍，通过视觉感觉是在移动，其实它是在新的坐标上重画）。本程序用方向键控制小电视移动（图5）。

四、缩放

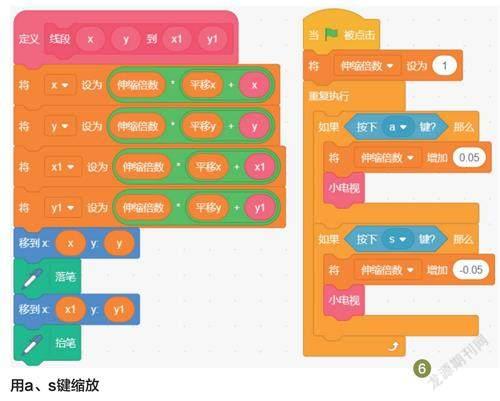
小电视的缩放其实就是在向量尾和向量头的坐标上分别对其放大或者缩小，也就是做乘法。通过新建变量“伸缩倍数”，用a、s键控制此变量增减，其值与线段函数积木参数的4个变量做乘法运算，以实现小电视的缩放功能（图6）。

五、基向量与三角函数实现旋转功能

1.基向量

在平面图形学中，有两个特殊的向量叫作标准基向量（也就是单位向量）。

i长度为1，方向指向X正方向的向量；j长度为1，方向指向y正方向的向量。

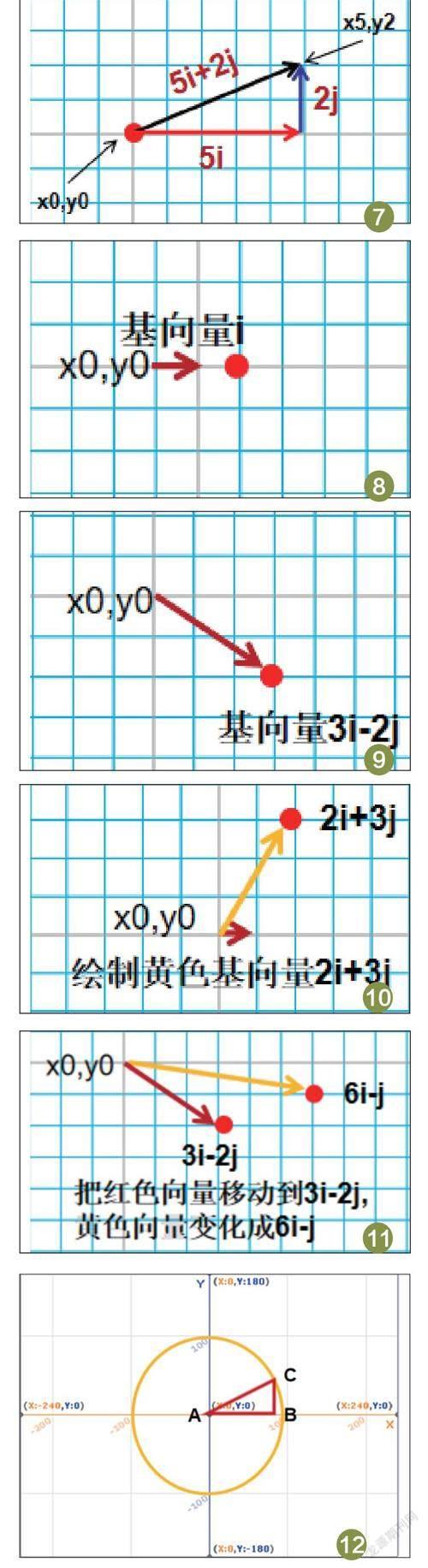
坐标表现如图7：

结论：图形的变化重点就是改变标准基向量（i，j）。

线性变化：通过改变基向量变化向量的操作。变化过程如图8-图11。

基向量i。

从i变化到3i-2j。

绘制黄色箭头向量2i+3j，红色向量回到i。

再把红色向量移动到3i-2j，黄色向量跟着变化到6i-j。

那么6i-j是怎么来的呢？

变化过程：变化的是i向量，j向量没变。

变化后新的基向量3i-2j带入到2i+3j中。

计算过程就是把i替换成3i-2j。得到的式子（2（3i-2j）+3j=6i-j）。

2.三角函数知识

A为圆，AC为半径r=1。点C做垂线相交在角A临边上点B形成了一个RT（直角三角形）。

根据三角函数关系（sinA=BC/AC=Y/1=y）；（cosA=AB/AC=X/1=x）。BC为sinA；AB为cosA。由上得出AB为X轴坐标值，BC为Y轴坐标值（图12）。

3.旋转

让小电视转起来，由“旋转度数”变量来控制，线段的长度在函数积木里面固定了，由于基向量的长度是1，通过三角函数知识算出新的基向量。从i分量开始，分量就是cosθ，y分量就是sinθ，转换后的i就是cosθ+sinθ；j分量就等于-cosθ+sinθ。我们就可以把带入到程序里面去，如图13。