隅撑控制钢梁面外稳定时檩条受力情况分析

孙 超

(中国中轻国际工程有限公司，北京 100026)

0 引言

门刚结构在厂房类建筑中广泛应用，对此类结构的工程认知和计算理论越来越深入，随着GB 51022—2015门式刚架轻型房屋钢结构技术规范[1](以下简称《新门规》)的发布实施，替代了原CECS 102:2002门式刚架轻型房屋钢结构技术规程[2](以下简称《旧门规》)，对一些习惯的计算方法进行了修正和调整，设计思路也随着新规范的提出有了一些新的变化。规范更新以后，隅撑仍然是控制钢梁平面外计算长度的主要措施，但《新门规》提出了新的计算公式来确定隅撑对工字钢梁计算长度的影响，而不再是《旧门规》时代，钢梁平面外计算长度直接取隅撑间距，具体内容详见《新门规》7.1.6条及条文说明，其中相关公式较为复杂，此处不赘述，可直接查阅规范原文。从规范公式可以看出，隅撑对钢梁的支撑作用是依靠檩条来实现的。从各方研究资料看，更多的关注钢梁的稳定分析。但在这个过程中，檩条和隅撑的相互关系，彼此影响如何，相对关注和研究比较少。本文从这个角度进行简单的分析，结合相关内容，抛砖引玉性的提出一些建议以利于指导工程实践。

1 隅撑-檩条体系简化模型

隅撑、檩条以及工字型钢梁通过螺栓或者焊接组成三角区域，当钢梁在荷载作用下，由于初始变形或荷载偏心等因素，受压翼缘出现向平面外弯扭屈曲变形的趋势，此时钢梁翼缘受到隅撑和檩条限制，阻止其发生失稳。隅撑-檩条支撑体系对工字型钢梁的约束简图如图1所示。

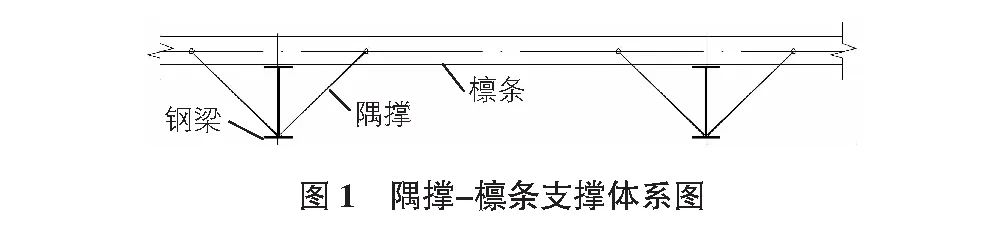
设置隅撑-檩条支撑体系的工字形截面钢梁发生侧向弯扭变形时，相邻钢梁的扭转变形可能同向，也可能反向。同一檩条相连的相邻工字形截面构件不同的失稳变形情况，导致檩条的变形可能为U形，也可能为S形。将工字形截面构件失稳时檩条变形为U形的变形状态称为U型失稳变形，将构件失稳时檩条变形为S形的变形状态称为S型失稳变形[3]。

失稳变形状态如图2所示。

《新门规》7.1.6条中的式7.1.6-4可以看出，隅撑的支撑刚度主要由檩条与隅撑协同工作下的檩条绕强轴的抗弯刚度提供，檩条、隅撑的轴向变形对支撑刚度的影响比较小。隅撑-檩条三角区域，构件线刚度较大，近似假设为刚性平面，在钢梁失稳时，会产生一个绕钢梁面外的扭矩，投影到平面上为弯矩记为M，而此弯矩需要由钢梁两侧连接的檩条中产生力矩来抵抗钢梁扭转。由于蒙皮效应的存在，屋面平面内刚度较大，轴向变形很小，变形而引起檩条轴力不起关键作用。上述抵抗力矩主要为两个垂直于檩条且方向相反的力形成的力偶来提供。为重点分析隅撑带来的檩条受力影响，使计算结果更为直观便于对比，这里先做一定简化，取钢梁两端檩条跨度、荷载相等，故产生的弯矩m1≈m2，m1=m1′=m1″，左右相互抵消，忽略弯矩的影响。从整体到局部分析此区域杆件的受力情况。隅撑-檩条受力简图如图3所示。

第一步：分析隔离体2，竖向力平衡：f1×sina=f2×sina；水平力平衡：f1×cosa+f2×cosa=n1+n2；弯矩平衡M=(n1+n2)×e。隔离体为对称结构，有f1=f2，n1=n2，得出f1×cosa=n1。f1=f2为隅撑轴力，n1=n2为檩条中轴力。

第二步：分析隔离体3，水平力平衡：n1+N1=f1×cosa；由第一步结果f1×cosa=n1，可得出N1=0(这里的N1=0不代表三角区外檩条没有轴力，而是相较于檩条面外抵抗力，三角区外檩条的轴力带来的抵抗力矩相对很小)。由竖向力平衡得F1=f1×sina。

第三步：整体分析隔离体2,3，水平力平衡得N1=N2=0；竖向力平衡的F1=F2；弯矩平衡得：M=F1×2L。

从上述构件内力分析结果看，初步得出结论：1)隅撑-檩 条体系在控制门刚梁平面外稳定时，为平衡扭矩会在檩条中产生垂直中性轴的力，会使檩条产生附加弯矩。2)隅撑-檩条体系在控制门刚梁平面外稳定时，隅撑使檩条内产生的轴力，主要集中在三角区域内部的檩条。

2 隅撑-檩条体系抗失稳中檩条的内力计算及分析

基于上述的内力分析，钢梁面外扭转失稳时，当产生的力方向同竖向荷载方向相同时，会使檩条的内力增加。工程常用的PKPM-STS钢结构工具箱计算檩条时，并未明确考虑此问题带来的影响。以往项目实践中，这个影响基本被忽略。由于设计冗余度的存在，以及其他不易完全计算清楚的有利作用，未见由此导致的安全问题。随着近年来，钢结构厂房设计不断被优化，应力比指标越来越接近上限，留给工程师无形的安全储备越来越有限，对本文所提的对安全不利因素应该更加重视起来。

以常用的檩条跨度、间距、隅撑尺寸为例，说明隅撑轴力对檩条的影响程度。选用常用的钢结构设计软件PKPM-STS工具箱为主要计算软件。以4跨连续檩条为例，分别用静力手册、PKPM-STS工具箱、PKPM-STS钢结构二维设计对比支座及跨中弯矩。计算简图如图4所示。每跨跨度7.0 m，计算以恒载(含自重)为例。活荷载在考虑活荷不利布置和一次性加载情况下，结论与恒载得出的一致。为对比三种算法弯矩计算结果的一致性，PKPM-STS工具箱计算时，连续檩条搭接处的刚度及承载力折减均按1.0输入。

对弯矩结果进行比对：PKPM-STS工具箱法较手册查表法低5%以内。PKPM-STS二维设计法较手册查表法相差±2%以内(见表1)。可见三种方法计算的弯矩结果误差允许。为了考虑隅撑杆件对檩条的影响，便于计算，后面主要采用PKPM-STS二维设计进行各种工况下檩条弯矩的计算。

表1 弯矩结果表

隅撑的轴力计算，依据《新门规》8.4.2条，公式如下：

N=Af/(cosθ)。

其中，A为被支撑翼缘的截面面积，mm2；f为被支撑翼缘钢材的抗压强度设计值，N/mm2;θ为隅撑与檩条轴线的夹角，(°)。

此公式是计算隅撑杆件的承载力，从公式可以看出，此轴力仅与支撑的翼缘面积、隅撑与檩条的夹角及翼缘钢号有关，与被支撑梁高、檩条尺寸、隅撑间距等均没有关联。用此轴力作为檩条的受力是偏于安全的。应注意此轴力为设计值，输入计算模型时应按荷载组合系数折减，可按1.3考虑。隅撑计算，在PKPM-STS工具箱中有对应模块。

隅撑支撑作用在《旧门规》6.3-4条中规定，计算檩条时，不应考虑隅撑作为檩条的支撑点。《新门规》中，未再规定此项要求。实际工程中，往往用STS工具箱的檩条模块设计，模块中也无法考虑此支撑的作用。同时隅撑对檩条的面外荷载是真实存在的，如果只是在原有基础上叠加考虑隅撑外力的作用，将导致檩条设计弯矩明显增加。笔者认为，对同一个原因引起的问题，既要考虑不利影响也要考虑有利因素。考虑隅撑轴力对檩条影响的同时，也应该计入隅撑的支撑作用[4]。

以下面算例为例说明檩条受力影响情况。取4跨等跨连续檩条，跨度7 m，檩条间距1.5 m，设两道拉条，檩条型号均取XZ220×75×20×2.0，双侧隅撑L56×3，支撑钢梁截面H700 mm×250 mm×6 mm×12 mm，隅撑与檩条夹角45°。恒荷载：0.3 kN/m2，活荷载：0.5 kN/m2。暂不考虑风荷载、施工荷载。

根据《新门规》8.4.2公式计算，隅撑轴力f1=f2=10.2 kN，F1=f1×sin45°=7.2 kN；按恒荷载换算标准值，F1k=7.2/1.3=5.5 kN；《新门规》不建议在端榀设置不对称隅撑，故不考虑端支座有隅撑。这里考虑端部第二榀和第三榀钢梁产生扭曲。各种情况简图如图5所示,图5中荷载为恒荷载，活荷简图不赘述。

对应上面各种工况的弯矩图如图6所示。

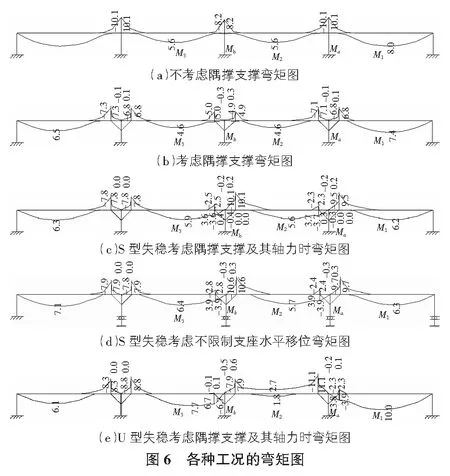
对应上面各种工况的钢结构应力比图如图7所示。

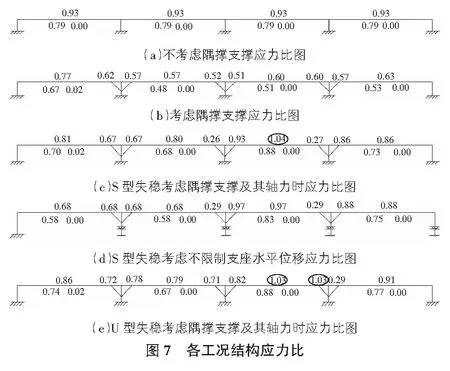
工况为基准工况，分别对比上面各工况结果：

1)对比图7(c)，图7(d)工况，支座的水平变形对檩条应力影响很小。

2)对比图7(a)，图7(b)工况，考虑隅撑支撑作用，檩条弯矩减小较多。

3)对比图7(b)，图7(c)工况，考虑隅撑支撑作用的同时，计入支撑产生的檩条外力，S型失稳状态，Ma,Mb,M2，支座及第二跨跨中增幅较大，其中支座Mb(c)已经大于Mb(a)。

4)对比图7(b)，图7(e)工况，考虑隅撑支撑作用的同时，计入支撑产生的檩条外力，U型失稳状态，Ma,Mb,M1，支座及第二跨跨中增幅较大，其中边跨M1(e)已经超过M1(a)较多。

5)弯矩不同幅度的增加，应力比结果表现不一样，主要是因为应力比以跨中和支座最大弯矩计算。

经过上述结果的对比分析，得出初步结论。由于S型、U型失稳状态是随机发生的，应以最不利结果控制。考虑隅撑支撑作用的同时，计入支撑产生的檩条外力，边跨跨中弯矩及支座弯矩影响较大。隅撑支撑的有利作用已经不足以抵消边跨跨中弯矩的增幅，实际工程中增加了不安全因素。

工程中，屋面连续檩条一般采用PKPM-STS工具箱进行设计。连续檩条支座应力计算考虑了檩条搭接后两个檩条断面叠合，虽然对强度进行了折减，支座处的应力比跨中低得多，但此时并不代表支座是安全的，因为常规设计时，搭接部分多数时候在隅撑与檩条连接点内，紧邻连接点内侧还存在一部分檩条是单檩条断面。而综合上述算例结果，可看出檩条最大弯矩会出现在隅撑与檩条连接点处，用PKPM-STS工具箱计算的檩条支座处的应力与不利点实际应力差距较大，存在安全隐患。另外，依本文1中受力分析可知隅撑与檩条连接点内侧檩条会产生附加轴力。结合上述两个因素，隅撑与檩条连接点处的断面往往会成为控制断面。

3 工程中屋面檩条安全现状分析

经过上述分析，隅撑-檩条支撑体系中，隅撑对檩条既有支撑作用，同时也产生外力，且一般外力的不利因素更加突出。以往实际工程中，很少考虑上述分析，但并未出现明显的安全问题，分析大体原因有如下几点：1)钢梁产生扭曲效应，是随着外荷载逐渐增加而产生的。只有大范围负荷面积内荷载接近极限设计值，上述效应才会凸显。2)相邻钢梁，同时失稳的概率较低，当只有一榀钢梁即将发生失稳时，附加作用的影响明显降低，本文仅列出相邻两榀钢梁同时失稳的数据。3)本文假定的隅撑轴力，是用于设计隅撑的，只与钢梁翼缘有关，不随檩条间距等变化而变化，实际轴力应该比按此方法计算的要小。4)屋面板与檩条整体空间效应的有利作用。5)设计中的冗余度以及结构安全系数等因素。

4 实际工程中应考虑的问题及建议

以往工程虽然考虑不足，由于各种有利因素的叠加，未出现明显问题，但不代表可以继续忽视相关实际影响。现在工程中，业主对用钢量控制越来越紧，往往会引入钢结构公司参与设计，从接触的钢结构公司看，钢结构公司的设计水平参差不齐，对规范的理解并不十分透彻，往往基于以往的工程经验进行设计。钢结构公司为了迎合业主对各项指标取值接近规范底限，使一些隐性的结构安全度不断的被压缩。设计人员如果对不利因素考虑不足，会产生一些意识不到的安全隐患。

针对本文提出的问题，提出以下几点操作建议：

1)对于连续檩条，檩条的搭接长度宜伸过隅撑与檩条交点。此时，此位置檩条截面近乎成倍增加，附加弯矩及附加轴力的作用足够抵消。在钢梁截面较大时，檩条按压弯构件核算，考虑蒙皮效应后，按纯弯计算。2)现在工程中，屋面已很少采用简支檩条，若由于其他原因(比如泄爆等)导致必须使用简支檩条，对于简支檩条，由于不存在搭接段，故需要按本文所述的受力情况进行复核，保证必要的安全度。3)若屋面檩条按PKPM-STS工具箱直接计算，而未单独考虑本文提到的不利影响时，端跨檩条跨中应力比宜小于0.75，中间跨檩条跨中应力比宜小于0.85。4)工程设计中，往往是设隅撑和不设隅撑的檩条取值一样，而基于本文的分析，在相同断面下，设与不设隅撑的檩条安全度明显不一致。故建议每道檩条处均设置隅撑，既能充分利用隅撑来控制钢梁平面外计算长度，同时也能使檩条的可靠度在同一个水平。

5 结语

本文通过对隅撑-檩条支撑体系的简要分析，得出了隅撑对檩条产生的附加外力会产生不利影响的结论。同时，根据计算比对，提出了简单的指导工程设计的建议。由于一些影响因素无法准确量化，分析计算方法相对简单，本文更侧重于提示相关安全问题，抛砖引玉引起各位设计师的重视。针对具体工程，结构设计师应有自己的判断和计算分析，满足檩条设计经济性的同时保证安全性。