白砂岩峰后蠕变力学行为试验研究★

谷亚军，李树清，黄 飞，陈国豪，朱颜平

(湖南科技大学资源环境与安全工程学院，湖南 湘潭 411201)

0 引言

由于工程扰动的影响，巷道围岩中会形成一个破裂区，在原岩应力作用下，破裂岩体会表现出较强的时间效应[1-2]，如破裂岩体的长期流变，这种现象很大程度上会影响巷道围岩控制的效果。因此，进一步研究岩石峰后流变力学特性是工程围岩稳定性控制至关重要的因素。

岩石峰后蠕变试验方面，Peng[3]发现破裂岩样在荷载作用下蠕变失稳时间较短。李晓、Jiang等[4-5]研究发现围压与破裂岩样的长期强度相关，随着围压的增大，峰后蠕变由非稳定型蠕变转化为稳定型蠕变。牛双建等[6]发现随着应力水平的提高，在各级应力水平下的总蠕变量呈指数关系增加。刘传孝等[7]通过拟合峰后单轴短时蠕变曲线，得出了基于Boltzmann函数的拟合曲线，确定了其待定系数且相关性较强。李树清[8]、谭玉林[9]、刘圣等[10]开展了砂质泥岩与红砂岩峰后蠕变关系的试验，发现岩石蠕变速率随应力增大而增大，蠕变失稳时间随应力增大而缩短，围压增量会降低岩石峰后蠕变速率，减缓蠕变过程，延长失稳时间。

上述研究对峰后蠕变力学特性进行了一些探索，但鉴于岩石种类复杂多样，有必要开展更多类型岩石的峰后蠕变试验，进一步确定石峰后蠕变力学特性。本文主要利用白砂岩试样在MTS815岩石力学试验系统上开展了峰后蠕变试验，并通过分析实验结果进而确定岩石峰后蠕变特性[11-15]。

1 试验准备及试验方法

1.1 试件准备

试验样品采自扬子地台区上二叠龙潭组地层，为白砂岩，呈灰白色，无明显裂隙和层理。根据国际岩石力学学会要求，将岩样经过钻取、切割以及打磨等工序加工成标准圆柱形试件，尺寸为φ50 mm×100 mm。为确保加工岩样的均质性，对其进行波速测定筛选出合适的试样。试验前对白砂岩岩样物理参数进行测量，试样具体的物理参数如图1所示。

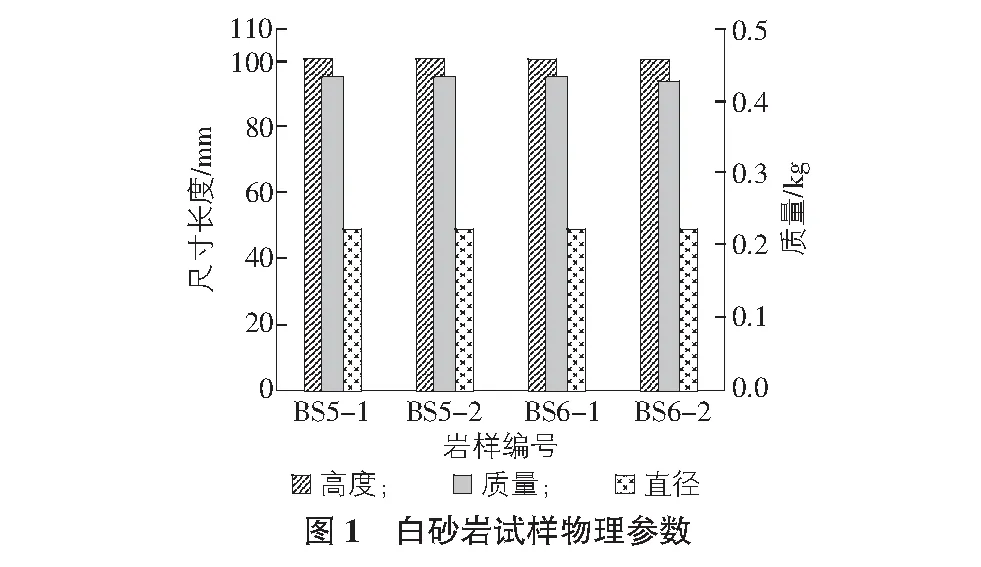
1.2 试验方法

基于MTS815电液伺服岩石试验系统开展白砂岩峰后蠕变测试实验。其中，围压选取10 MPa和15 MPa两个等级，蠕变加载水平设置在岩石峰值强度的30%～60%处，轴向应力差值为2 MPa～4 MPa，待系统加载至预定值后保持12 h，如图2所示的加载路径。根据图2所示，该蠕变实验分为预加载、轴向位移加载、变形稳定及分级蠕变共4个阶段。其中，预加载阶段表示将轴压与围压同时加载到设计数值；轴向位移加载阶段表示保持围压不变，轴向以位移加载模式加载至峰后设计数值；变形稳定阶段表示保持试件轴向位移恒定至轴压与围压基本稳定；分级蠕变阶段表示控制轴压逐级加载至设计数值并稳压保持。

2 试验结果与分析

2.1 峰后蠕变曲线特征

鉴于蠕变阶段时间较长，本次试验主要开展了4组峰后蠕变实验，测试获得了如表1所示的岩石力学参数，并绘制了如图3所示的分级加载峰后蠕变曲线和图4所示的试件峰后各级蠕变特征参数直方图。

表1 白砂岩力学特征参数

由图3可知，4种白砂岩试样峰后的分级加载峰后蠕变曲线由两部分组成：等速蠕变、加速蠕变，曲线均未有明显的衰减蠕变。由表1，图4可知，4种白砂岩试样发生加速蠕变阶段的应力基本为其峰值强度的50.23%～57.39%应力水平处。4种岩样发生蠕变破坏的应力水平虽存在部分的差异，但总体的峰值强度较为接近。

2.2 峰后蠕变量与应力水平之间的关系

由图4可知，围压为15 MPa的试件BS15-1和BS15-2加速蠕变阶段蠕变量占总蠕变量的比例分别为73%左右，而围压为10 MPa的试件BS10-1和BS10-2占比却为71.61%和65.09%；试样在这两个阶段的蠕变变形之比分别为2.7,2.8,2.5,1.86。由此可见，试件峰后蠕变主要出现在加速蠕变时期，该时期试件短时间产生较大的蠕变变形是导致白砂岩蠕变失稳破坏的重要原因。

依靠试样峰后各级应力状态下的蠕变量，绘制如图5所示的蠕变量-应力水平关系图。

对4个试样的蠕变量-应力水平关系进行拟合，得到其各自的回归曲线，具体关系式如下：

BS15-1：ε=0.134 1+1.657 2×10-12×e0.601 9σ，R2=0.999。

BS15-2：ε=0.179 7+3.802 0×10-14×e0.633 9σ，R2=0.999。

BS10-1：ε=0.359 9+7.515 7×10-12×e0.693 2σ，R2=0.988。

BS10-2：ε=0.447 6+1.014 6×10-8×e0.502 8σ，R2=0.989。

由图5可以看出，各级峰后蠕变量与应力水平呈指数函数关系，白砂岩的峰后蠕变分为以下3个阶段：依次是等速蠕变、加速蠕变、蠕变失稳。

2.3 峰后轴向蠕变与径向蠕变的对比分析

由于实验过程中MTS815试验机的环向传感器发生故障，试件BS10-1和BS10-2的径向蠕变数据采集发生错误，因此本节仅以试件BS15-1和BS15-2实验数据进行分析。通过叠加原理分析试样数据后，得到其分级加载峰后轴向与径向蠕变曲线，如图6所示。

由图6可知，在围岩保持不变时，试件的各级径向蠕变量随应力水平的增大而增大，且在最后一级应力水平下，轴向蠕变量增大程度明显比径向蠕变量的大。峰后径向蠕变参数试验结果见图7。

由表1和图7可知，试件径向总蠕变量总体比轴向总蠕变量要小。试样发生等速蠕变时，轴向蠕变量比径向蠕变量要小，主要发生径向蠕变；而在加速蠕变时，轴向蠕变量比径向蠕变量大，主要发生轴向蠕变。对于白砂岩不同蠕变阶段的特性，采取不同的应对措施。

2.4 峰后蠕变破坏特征

白砂岩峰后蠕变的破坏形态如图8所示。

由图8可知，试样破坏形态主要为单一剪切破坏，在不同围压和轴向压力作用下，试样的破坏形态并没有出现明显差异。

3 围压对峰后蠕变的影响

3.1 围压对峰后蠕变速率的影响

根据图2的白砂岩峰后蠕变曲线获得了白砂岩峰后蠕变速率均值和加速蠕变阶段维持时间，如表2所示。

表2 白砂岩峰后蠕变速率均值

由表2可知，除试件BS10-1第2级蠕变速率均值外，围压15 MPa比围压10 MPa下的蠕变速率均值有一定程度的减小，而加速蠕变维持时间有一定程度的增长。这说明，围压变化对白砂岩峰后蠕变特性有一定的影响，增大围压，可以在一定程度上降低白砂岩的峰后蠕变速率。

3.2 围压对峰后蠕变量的影响

围压10 MPa下的蠕变破坏应力水平均比围压15 MPa下第一级应力水平要小，而围压10 MPa下的各级蠕变量均大于围压15 MPa下的各级蠕变量。

在蠕变失稳时间方面，围压10 MPa下蠕变失稳持续时间分别为36.09 h和36.03 h，围压15 MPa下的蠕变失稳持续时间为38.32 h和42.61 h，围压15 MPa下的蠕变失稳持续时间总计比围压10 MPa时延长了2.23 h以上。

综上所述，围压和白砂岩的峰后蠕变特性相关。各级应力水平下的峰后蠕变速率随围压的增大而降低，从而增加白砂岩蠕变失稳时间，改良岩石的峰后蠕变特性。

4 结论

1)各级峰后蠕变量与应力水平呈指数函数关系，白砂岩的峰后蠕变依次是等速蠕变、加速蠕变、蠕变失稳。

2)试件径向总蠕变量比轴向总蠕变量小。轴向蠕变量和径向蠕变量在不同蠕变阶段存在一定区别，当岩样为等速蠕变时主要发生径向蠕变，而岩样为加速蠕变时主要发生轴向蠕变。

3)试样破坏形态主要为单一剪切破坏，在不同围压和轴向压力作用下，试样的破坏形态并没有出现明显差异。

4)白砂岩的峰后蠕变特性对围压的影响较敏锐。增大围压能够在一定程度上降低白砂岩的峰后蠕变速率，从而增加蠕变失稳时间。