芬斯勒流形上的两个重要不等式①

程新跃，张希滨

重庆师范大学 数学科学学院， 重庆 401331

芬斯勒几何是黎曼几何的一种自然推广， 是没有二次型限制的黎曼几何. 与黎曼几何的情形相似， 在Ricci曲率有下界的条件下， 芬斯勒流形上有着非常丰富的几何与分析性质[1-2]. 文献[3]定义了芬斯勒几何中的加权Ricci曲率. 文献[4]建立了Bochner公式及相应的不等式. Bochner公式及相应的不等式在芬斯勒流形上的几何与分析问题的研究中有着极为深刻的影响. 利用逐点Bochner-Weitzenbock公式和积分型Bochner-Weitzenbock公式， 文献[5]在芬斯勒流形的加权Ricci曲率RicN有下界的条件下， 得到了Poincare-Lichnerowicz不等式. 文献[6]给出了芬斯勒流形上的p(>1)-Bochner-Weitzenbock公式和p-Reilly型公式， 并且在加权Ricci曲率RicN有下界的n维芬斯勒流形上， 得到了无边或带有凸边界的紧致芬斯勒流形上的p-Poincare不等式. 文献[7]在芬斯勒流形的加权Ricci曲率RicN有下界的条件下， 得到了芬斯勒Laplacian第一非零Neumann特征值的下界估计. 文献[8]则在加权Ricci曲率Ric∞有下界的完备芬斯勒测度空间中得到了芬斯勒Laplacian第一特征值的下界估计.

本文的主要目的是在加权Ricci曲率RicN有正下界的芬斯勒流形上导出重要的泛函不等式和几何不等式. 主要研究结果由两部分组成： 首先， 我们给出了芬斯勒流形上优化的Poincare-Lichnerowicz不等式； 其次， 我们得到了芬斯勒流形上Laplacian第一特征值的一个优化的下界估计.

定义

这里，F(x，y)为给定的芬斯勒度量，S(x，y)为S-曲率.

本文的主要结论如下：

定理1设(M，F，m)是一个可测的紧致无边的芬斯勒流形， 且满足RicN≥K>0， 其中N∈(n， ∞).对任意的f∈H1(M)， 设(ut)t≥0是满足u0=f的热方程的整体解， 则

(1)

其中Varm(f)表示f的方差，g(t)=g∇ut(∇∇utF(∇ut)， ∇∇utF(∇ut)).

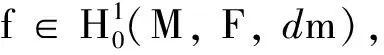
(2)

我们称λ1是(M，F，m)的第一特征值.一个很自然的问题就是研究芬斯勒流形上Laplacian第一特征值的下界估计.我们在RicN有下界的紧致芬斯勒流形上得到了芬斯勒Laplacian第一特征值的一个新的下界估计.

定理2设(M，F，m)是一个可测的紧致无边的芬斯勒流形， 且满足RicN≥K>0， 其中N∈(n， ∞).则当第一特征值λ1>0时， 有

(3)

(1)式和(3)式分别给出了紧致芬斯勒流形上的Poincare-Lichnerowicz不等式和芬斯勒Laplacian第一特征值的下界估计， 分别改进了文献[5，9]中的相关不等式.

1 预备知识

给定一个n维C∞流形M，F是流形M上的芬斯勒度量， 记F的Busemaun-Hausdorff体积形式为

dm=σ(x)dx1∧…∧dxn

其中体积系数σ(x)定义为[10]

这里， Vol表示欧氏体积，Bn(1)表示Rn上的标准单位球. (M，F，m)的S-曲率可以表示成

其中Gi是F的测地系数.

(4)

当N→∞和N↓n时， 可定义如下的加权Ricci曲率：

Ric∞(v)=Ric(v)+ψ″η(0)

(5)

事实上， 容易得到ψ′η(0)=S(x，v)就是芬斯勒几何中关于测度m的S-曲率， 且

其中“|”表示关于Chern联络的水平协变导数[11].因此， 可以进一步把RicN(v)写成[12]

一般地， 若对任意的x∈M和切向量v∈TxM， 总有RicN(v)≥KF2(x，v)(这里K为实常数)， 则RicN≥K.

∇u(x)=L-1(du(x))∈TxM

因此， 在局部坐标下， ∇u可以写成[12]

(6)

其中

Mu={x∈M|du(x)≠0}

g*ij(x， du)为F的对偶芬斯勒度量F*的基本张量， 且

g*ij(x， du)=gij(x， ∇u)

给定流形M上的一个光滑测度m， 对应的体积形式为

dm=σ(x)dx1∧…∧dxn

Δu=divm(∇u)

(7)

等价地， 我们在弱的意义下定义函数u的Laplacian为满足以下条件的Δu： 对所有的

(∇u)dm

由Laplacian及散度定义， 对流形M上任意的光滑函数φ， 有

divm(φ∇u)=φΔu+dφ(∇u)

(8)

gV(X，Y)=gij(x，V)XiYj

特别地，gV(V，V)=F2(x，V).在加权黎曼流形(M，gV，m)上， 可定义线性梯度向量场与线性Laplacian分别为

ΔVu=divm(∇Vu)

(9)

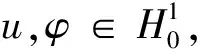
其中λ=E(u).根据Laplacian弱定义， 上式等价于

Δu+λu=0

我们分别称λ和u是(M，F，m)的一个特征值和特征函数.

接下来介绍非线性热方程

(i) 若c≤u0≤C几乎处处成立， 则当t>0时，c≤ut≤C几乎处处成立；

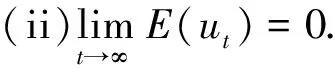
本文中， 我们总假定ΛF<∞.

2 若干重要的引理

设(M，F，m)是测度可测的芬斯勒流形. 为了证明定理1， 我们需要一些必要的引理.

引理2[4]给定u∈C∞(M)， 则在Mu={x∈M|du≠0}上， 有

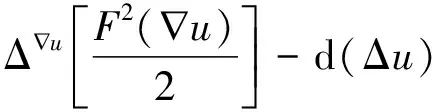
当Ric∞≥K时， 有

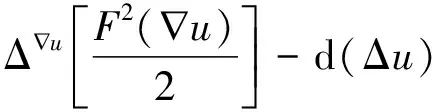
其中‖·‖HS(∇u)表示关于度量g∇u的Hilbert-Schmidt范数， ∇u表示u的梯度向量场， Δu表示u的Laplacian.

根据引理2及(4)，(5)式， 可以得到以下结果：

命题1给定u∈C∞(M)及N∈(n， ∞)， 则在Mu={x∈M|du≠0}上有

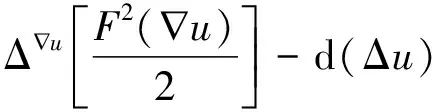
(10)

及

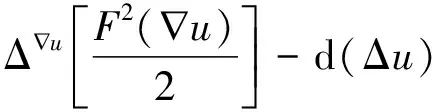
(11)

易见， (11)式比文献[4]中相应的不等式更优.进一步， 类似于文献[4]的讨论， 我们可以用同样的方法得到下面的积分型不等式：

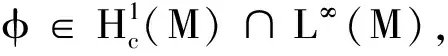
(12)

这里， 我们用到了

d[F(∇u)](∇∇u[F(∇u)])=g∇u(∇∇uF(∇u)， ∇∇uF(∇u))

根据引理1， 取测试函数φ=1， 可以得到以下引理：

引理3若(M，F，m)是紧致无边的芬斯勒流形， 且满足RicN≥K， 其中N∈(n， ∞)且K∈R.给定u∈H2(M)∩C1(M)， 使得Δu∈H1(M)， 则有

(13)

由于(M，F，m)是紧致的芬斯勒流形， 我们可以将m标准化使得m(M)=1.定义f∈L2(M)的方差为

此外， (ut)t≥0是满足u0=f的热方程∂tut=Δut的整体解， 则对任何f∈H1(M)， 根据线性化热半群的性质， 在L2(M)中有质量守恒[4]

和遍历性[6]

引理4[4]设(ut)t≥0是热方程的整体解.则对所有t>0， 有

几乎处处成立.

3 主要定理的证明

定理1的证明设(ut)t≥0是满足u0=f的热方程的整体解.令

那么根据遍历性可得

且

(14)

根据Φ(t)的定义， 我们知道

(15)

由引理4， 对t>0， 我们有

由定义，S(∇u)2≥ω2F2(∇u). 根据引理3， 有

从而有

最后，

其中

g(t)=g∇ut(∇∇utF(∇ut)， ∇∇utF(∇ut))

由(15)式得

(16)

这就完成了定理1的证明.

作为引理3的应用， 定理2的结果是自然的.

定理2的证明通过假设和引理3， 我们得到

因为Δu=-λu， 我们有

进一步， 有

这表明

从而， 我们有

因此， 由(2)式我们得到

这就完成了定理2的证明.