基于LLE-OS-ELM的锂离子电池热过程在线建模

吕 洲,何 波,李志德

(1.广州港科大技术有限公司,广东 广州 511458; 2.清华大学深圳国际研究生院,广东 深圳 518055)

锂离子电池使用过程中会产生热量,过高的温度会加速老化,甚至自燃、爆炸[1]。建立准确的电池热过程模型,有利于优化、监测和控制电池系统,提升使用过程的性能、寿命和安全性等。锂离子电池的热过程是一类典型的时变分布参数系统,具有时变及强非线性特征,导致建模困难。

目前,不少学者针对锂离子电池热过程的模型原理展开了研究。宋文吉等[2]结合电池等效电路,构建具有分层结构的电-热耦合模型,获得电池的温度分布,该模型的预测结果与传感器测量的温度较为吻合。戴海燕等[3]结合质量守恒、能量守恒和电池内部电化学反应等理论,建立单体电池的电化学-热力学耦合模型,在2C倍率放电实验中,温度预测误差在0.925%以内。为研究极端条件下的电池热失控行为,张培红等[4]建立三元正极材料锂离子电池的热滥用模型。在直接接触式加热实验中,该模型得到的电池表面平均温度与实验测量值在时间上的变化趋势一致,具有较高的适用性。上述方法都属于离线模型,无法反映电池物性参数时变条件的热力学行为。尽管许多基于模型的在线方法,如基于电-热耦合的在线建模方法[5],得到广泛应用,但常适用于模型已知的情况,还有较多参数需要辨识,模型计算复杂度较大,因此,部分学者开始转向基于卡洛南-洛伊(KL)方法的纯数据在线时空模型[6-7],但KL方法是一种忽略非线性信息的全局线性降维方法,不能揭示热过程的强非线性特征。

为解决模型未知的强非线性锂离子电池热过程在线建模问题,本文作者提出基于局部线性嵌入(LLE)方法和在线顺序超限学习机(OS-ELM)的在线建模方法。首先,利用LLE实现电池温度数据的非线性时空解耦;然后,使用OSELM构建在线时序模型;最后,通过时空综合,重构完整的温度分布。

1 锂离子电池热过程在线建模方法

1.1 问题描述

锂离子电池的热过程是一类典型的无限维分布参数系统,控制方程可表示为[8]:

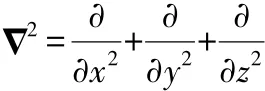
电池的边界条件可描述为:

式(2)中:h为对流换热系数;Tair为环境温度。

由式(1)、(2)可知,锂离子电池热过程模型构建的难点在于:温度分布具有时间/空间耦合特征,实现精准解耦操作是建模的关键;电池的密度及比热容等物性参数均与温度有关,但温度是时间的函数,且环境温度是一个变量,时刻变化;Q(S,t)函数涉及一系列复杂的物理/化学变化,难以准确建立偏微分方程。

1.2 建模框架

假设由温度传感器采集到锂离子电池温度数据为{T(S,ti),S=1,2,…,NS;i=1,2,…,Nt},其中NS为温度传感器的数量,Nt为总时间;锂离子电池的输入信号为{u(ti)=[E(ti),I(ti)]T,i=1,2,…,Nt},其中u(ti)∈ℝ2为输入向量,E(ti)为电池电压,I(ti)为电池电流。

如图1所示,首先通过构建LLE模型,将电池温度数据T(S,t)分离成空间基函数及时间系数。根据傅里叶变换,T(S,t)可以时空解耦为:

图1 建模框架Fig.1 Modeling framework

式(3)中:φi(S)为单位正交的空间基函数;ai(t)为时间系数;N为模型的阶数。

图1中:(t)为预测的时间系数;(S,t)为重构的温度值。

当获得a(t)=[a1(t),…,aN(t)]T∈ℝN后,基于 OSELM构建u(t)与a(t)间的动态时序模型。一般而言,非线性时序模型可表示为:

式(4)中:da为最大输入延时;du为最大控制延时;F为需要使用OS-ELM拟合的未知函数。

最后,根据式(3)重构温度分布,得到式(5)。

1.3 局部线性嵌入(LLE)方法

局部线性嵌入(LLE)方法是一种利用局部邻域的线性关系实现全局非线性降维的方法。

以向量T(∶,ti)为例,如图2所示,利用欧氏距离选择T(∶,ti)的K个近邻,作为集合Qa(i),并设计重构公式为:

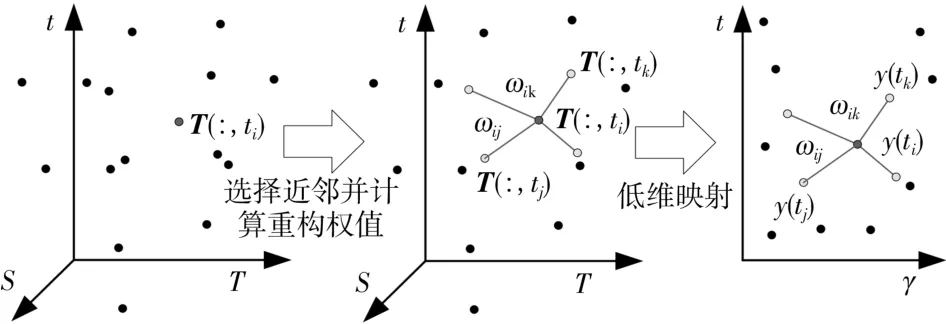
图2 向量T(∶,ti)的LLE流程Fig.2 Modeling process of local linear embedding(LLE)of vector T(∶,ti)

式(6)中:T(∶,tj)为T(∶,ti)的K近邻向量;ωij为重构权值向量ωi的元素。

为求出向量ωi,设计目标函数:

利用KKT条件求解式(7),获得重构权值为:

式(8)中:Cm为局部协方差矩阵,其元素为(Cm)pq=[T( ∶,ti)-T( ∶,tp)]T[T( ∶,ti)-T( ∶,tq)]|p,q∈Qa(i);l=(1,…,1)T∈ℝK,为元素为1的向量。

假设T(∶,ti)在低维度对应的投影为y(ti),K个近邻点对应的投影为,则最小化损失函数ε(Y)为:

式(9)中:Y=[y(t1),…,y(tNt)];Ii为单位矩阵I的第i列;(W)ij=ωij,为权值向量的矩阵形式;Wi为矩阵W的第i列;tr为矩阵的迹;M=(I-W)(I-W)T。

为最小化式(9),构建函数L(Y,λ):

式(10)中:λ为拉格朗日乘子。

对式(10)求导并为0,得到:

式(12)中:λ′=-λ。

假设求得M的特征值为λ′0＜λ′1＜…＜λ′Ni,舍弃特征值为λ′0的特征向量,则特征值(λ′1,…,λ′Ni)所对应的特征向量即为式(12)的解。为确定式(3)中的阶数N,使用式(13)计算系数η:

在特征值(λ′1,…,λ′Ni)中,从大到小选择,当η≥0.99时,即可确定阶数N。最终特征值(λ′N,…,λ′Ni)所对应的特征向量即为所得YT。基于快照法,空间基函数使用式(14)计算:

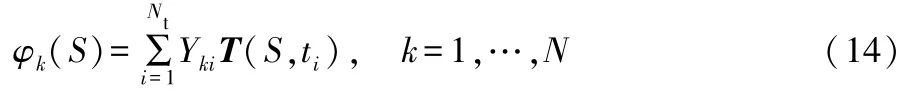
式(14)中:Yki为矩阵Y的第k行第i列元素。

1.4 基于OS-ELM的在线时序模型

1.4.1 初始学习阶段

在初始学习阶段,ELM利用初始数据集א0,将模型输入z(t)及模型输出a(t)表示为:

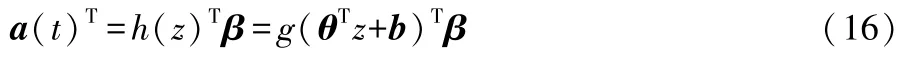
式(16)中:h(z)∈ℝNh,为隐含层输出;Nh为隐含层节点数;β∈ℝNh×N,为输出权值;g为激活函数;θ∈ℝ(N+2)×Nh,为输入权值;b∈ℝNh,为隐含层阈值;θ及b为随机生成的变量。

式(16)中,只有β为未知参数。假设Nt＞Nh,则β可由式(17)获得:

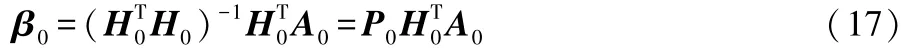
式(17)中:H0={h[z(2)]T,…,h[z(Nt)]T}∈ℝ(Nt-1)×Nh,为隐含层输出的矩阵形式;,A0=[a(2),…,a(Nt)]∈ℝ(Nt-1)×Nh,为输出矩阵。

1.4.2 在线序列学习阶段

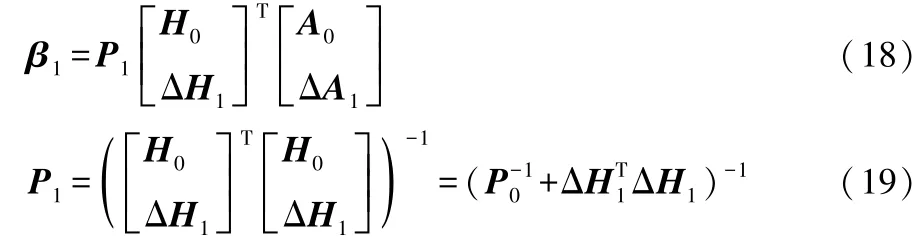
式(18)中:ΔH1={h[z(Nt+1)]T,…,h[z(Nt+L1)]T}T,为א1的隐含层输出;ΔA1=[a(Nt+1),…,a(Nt+L1)],为相对应的模型输出。

根据Woodbury公式,P1可化简为:

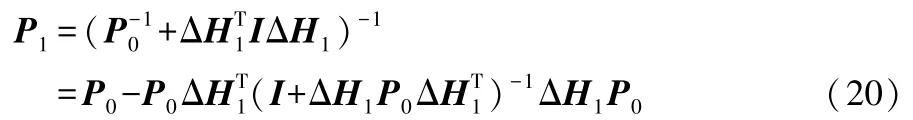
式(18)最终可表示为:

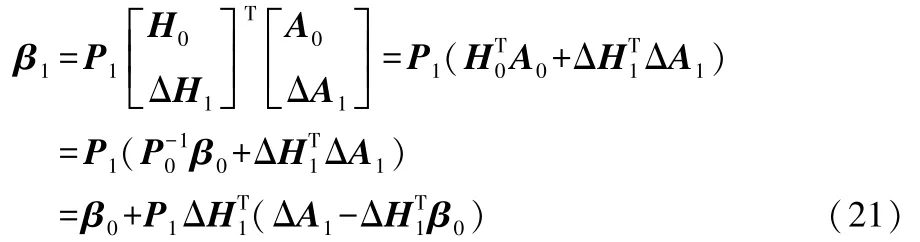
结合更新的输出权值,在线时序模型可表示为:

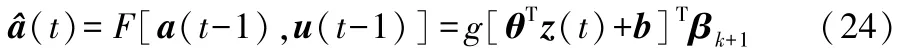
一旦获得时间系数,即可用式(5)重构电池温度分布。

2 实验验证

2.1 实验设置

实验采用三元正极材料软包装锂离子电池(佛山产),额定容量为32 Ah,额定电压为3.7 V,长度、宽度分别为240 mm、156 mm,厚度为8 mm。该锂离子电池的长和宽比厚度大得多,因此实验过程仅考虑二维平面温度。30个PT150接触式温度传感器(深圳产)均匀分布在电池表面,用于采集电池温度,如图3所示。

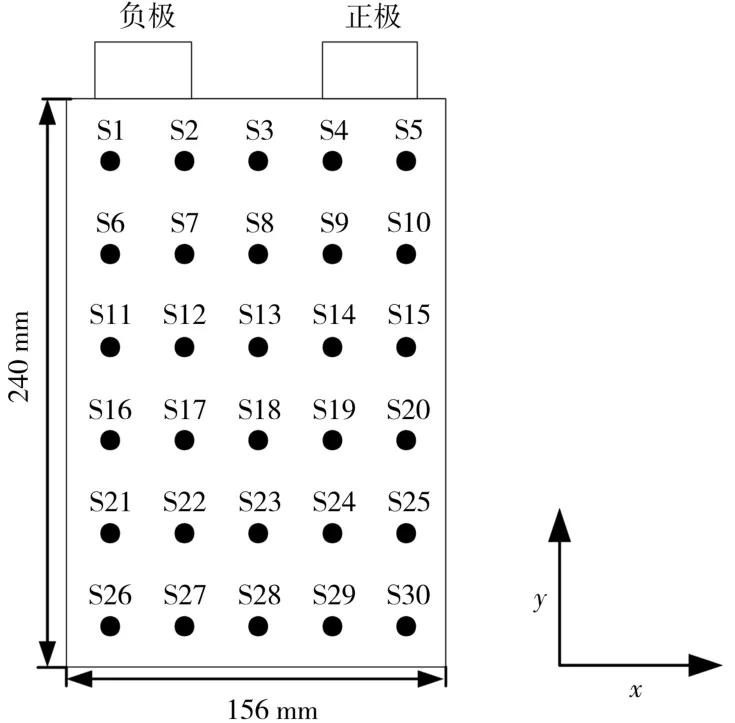
图3 三元正极材料软包装锂离子电池温度传感器的分布Fig.3 Distribution of temperature sensors of the ternary cathode material pouch Li-ion battery

为充分激发电池温度,充电电流及相应电压见图4。

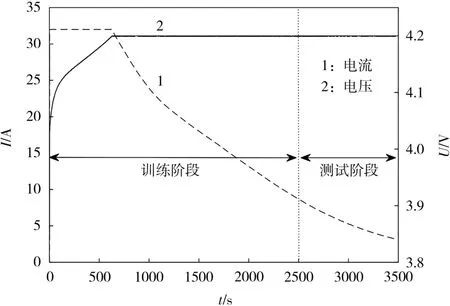
图4 三元正极材料软包装锂离子电池的充电电流及电压Fig.4 Charging current and voltage of the ternary cathode material pouch Li-ion battery

为验证所提方法对未知温度边界的响应能力,将锂离子电池放置在温控箱内,温度控制在25～30℃。整个实验过程维持3 474 s,充电电流、电压及电池温度每1 s采集一次,共得到3 474组数据。为验证所提出的模型,将前2 500组数据用于模型训练,后974组数据用于模型在线测试。

仿真开始前,需要将所有数据归一化到[-1,1]之间,算法参数设置如下。

①LLE方法,近邻数K=20;②OS-ELM方法,隐含层节点数Nh=50,激活函数g为Sigmod函数,输入权值θ及隐含层阈值b均在区间[-1,1]中随机生成,在线测试过程中,每次到达的新数据集אk+1的数据大小,Lj均取5。

2.2 结果分析

图5为3 000 s时电池表面的温度分布。

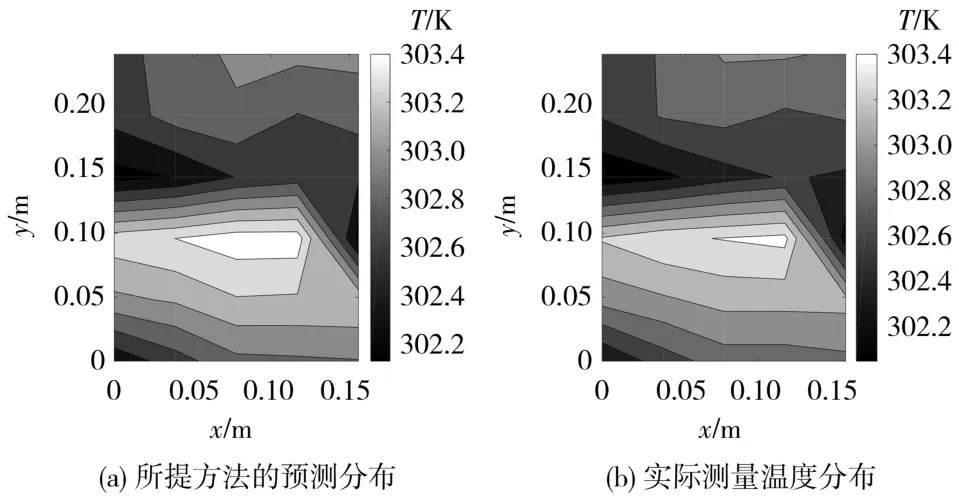
图5 3 000 s时电池表面温度对比Fig.5 Comparison of battery surface temperature at 3 000 s

从图5可知,所提出的在线时空建模方法得到温度分布与实际测量的近似。

在同样的实验参数设置下,LLE-ELM及所提出的在线建模方法在3 000 s时锂离子电池表面温度的绝对相对误差(ARE)[8]结果见图6。

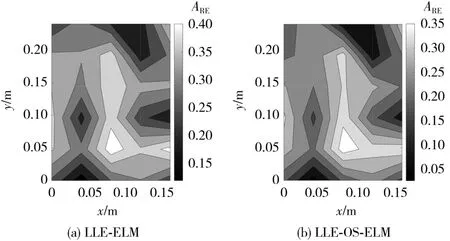
图6 3 000 s时A RE结果Fig.6 Absolute relative errors(A RE)results at 3 000 s

从图6可知,在3 000 s时,LLE-ELM的ARE值在0.40以内,而所提方法的ARE值在0.35以内。这是因为所提方法是一种在线模型,可实时利用新到达的数据改善建模性能,而LLE-ELM是一种离线建模方法,对锂离子电池热过程时变行为的适应能力较弱。

后974组测试数据的时间标准绝对误差[8](TNAE)仿真结果见图7,其中KL-OS-ELM为整合KL与OS-ELM的时空建模方法,而Th2Sim为在线的电-热建模方法[5]。

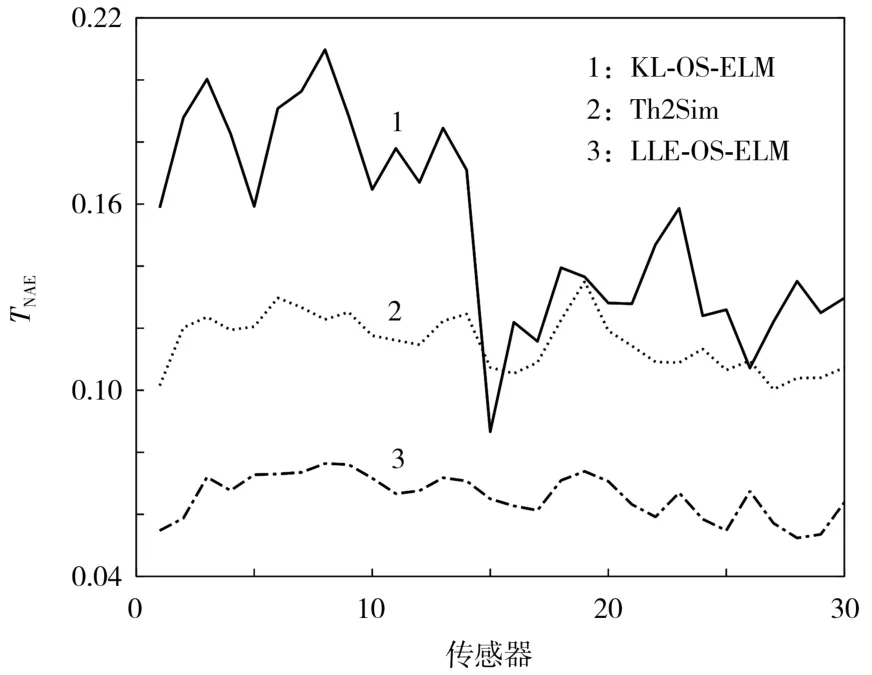
图7 3种方法的T NAE对比Fig.7 Comparison between three methods in temporal normalized absolute error(T NAE)

从图7可知,所提出方法的TNAE在[0.052 4,0.076 4]之内。这表明,与KL-OS-ELM及Th2Sim相比,所提方法在时间方向有更好的建模性能。

3种方法的仿真时间与均方根误差[8](RMSE)结果如表1所示。

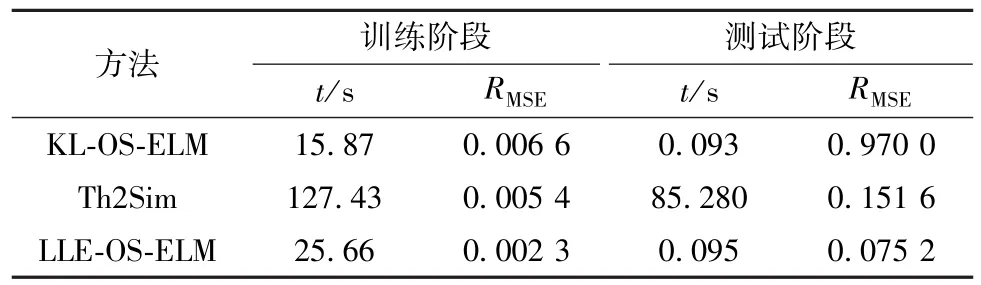
表1 模型性能对比Table 1 Comparison of model performance

从表1可知,KL-OS-ELM在数据训练阶段有较好的时间学习优势,但在测试阶段,RMSE明显差于LLE-OS-ELM。这是因为尽管KL-OS-ELM能够实现在线学习,但KL方法是一种全局线性降维方法,学习时间虽短但无法精确反映锂离子电池热过程的非线性特性。Th2Sim尽管具有较好的RMSE值,但热分布模型需要使用有限元方法求解,计算时间偏长。

相比于传统热过程建模方法,所提方法具有以下优势:①所提方法是一种数据驱动方法,能够解决电池模型未知时的建模问题;②LLE方法是一种流形学习方法,能够实现锂离子电池热过程的温度数据的非线性降维;③基于OS-ELM的在线时序模型可以实现模型的实时更新,解决锂离子电池热过程的时变行为捕捉问题。

3 结论

本文作者提出基于LLE和OS-ELM的锂离子电池热过程在线时空建模方法:首先,使用LLE方法实现锂离子电池温度场的非线性时空解耦,由此获得时间系数;然后,提出基于OS-ELM的时序模型,实现锂离子电池热过程的在线学习;最后,通过时空整合,重构电池温度分布。相比于部分现有的建模方法,所提方法可将TNAE控制在[0.052 4,0.0764]之内,RMSE则达到0.075 2。此外,在相同条件下,所提方法表现出仿真时间较短的优势,适用于实时应用的情景。