基于FCM聚类与BO算法的PEMFC故障分类

卢忠昌,刘芙蓉,杨 扬,2*,谢长君,2

(1.武汉理工大学自动化学院,湖北 武汉 430070; 2.武汉理工大学汽车工程学院,湖北 武汉 430070)

质子交换膜燃料电池(PEMFC)具有高效率、低噪声和零排放等优点,受到广泛关注[1]。为解决燃料电池故障诊断问题,文献[2]基于故障数据构建时序序列,训练长短期记忆(LSTM)模型对故障序列进行分类,准确率为95%。文献[3]提出一种基于离散区间二进制序列脉冲信号的燃料电池电化学阻抗谱(EIS)在线测试及故障诊断方法,利用粒子群优化支持向量机(PSO-SVM)算法对电堆故障进行诊断,准确率为96%。文献[4]提出一种基于卷积神经网络的故障诊断方法,通过图像信号提取故障诊断特征进行分类,分类准确率达100%,但诊断周期约为2.08 s,不能完全满足在线检测要求。文献[5]提出基于反向传播神经网络的燃料电池故障诊断方法,通过提取特征向量,采用BP神经网络作为模式分类器进行故障诊断,准确率达94.95%。

在不增加测量设备的前提下,为进一步提高燃料电池故障分类准确率,本文作者提出一种基于模糊C均值(FCM)聚类与贝叶斯优化(BO)算法的故障分类方法,在MATLAB中对实验数据聚类分析、构建分类模型并进行仿真,旨在验证所提方法的可行性。

1 EIS测试方法

为判别燃料电池的水淹及膜干故障,对燃料电池内部阻抗的提取尤为重要。EIS测试原理图见图1。

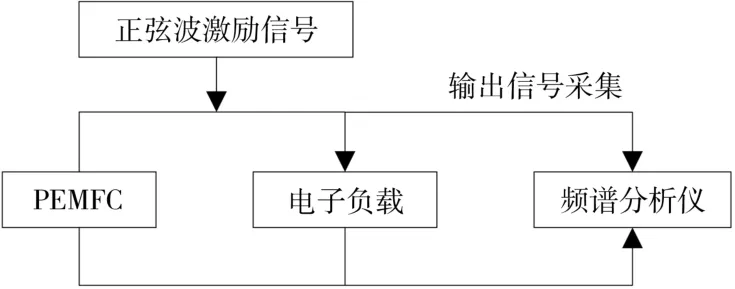
图1 EIS测试原理图Fig.1 Schematic diagram of electrochemical impedance spectroscopy(EIS)test

如图1所示,燃料电池EIS测试是指向燃料电池施加一个较小的正弦电压激励信号,然后测定系统的电流响应信号。一个系统的正弦阻抗响应Z可以表示为:

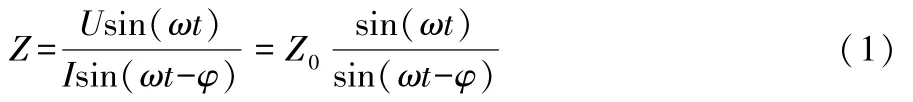
式(1)中:Z0是阻抗模值;U是电压模值;I是电流模值;φ是阻抗相移;ω是角频率;t是时间。

用频谱分析仪分别测得燃料电池的电压和电流,计算不同频率下的阻抗模值和相位差,即可绘制Nyquist图,用于燃料电池故障诊断。

2 PEMFC等效电路拟合

对燃料电池EIS数据的分析,要基于等效电路模型进行阻抗拟合。含恒相位元件(CPE)的Randles等效电路模型如图2所示。

图2 含恒相位元件(CPE)的Randles等效电路模型Fig.2 Randles equivalent circuit model including constant phase element(CPE)

图2中:Q是CPE的模值;α是CPE的相位;Rm是欧姆电阻;Rp是极化电阻;Zδ是Warburg扩散阻抗。

选择含有限扩散阻抗的Randles等效电路,电路中包含Rm、Rp、Zδ和 CPE 等 4个电子元件,由 Butler-Volmer方程和Fick第二扩散定律,可推导出Zδ的一般表达式:

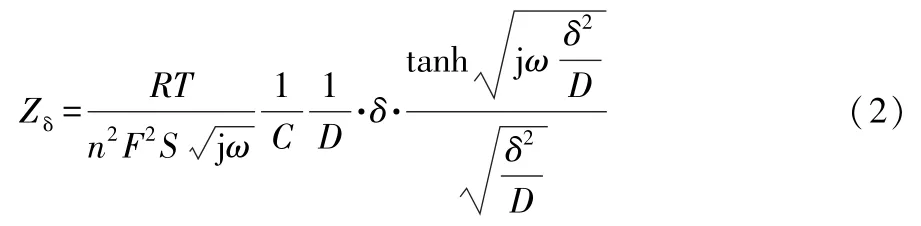
式(2)中:C是阴极活性层氧浓度;D是扩散系数;F是法拉第常数;T是温度;j是虚部单位;n是电子数;R是理想气体常数;S是电池活化面积;δ是扩散层宽度。

定义时间常数τd及阻抗Rd:

可得到Warburg扩散阻抗的表达式:

等效电路中,恒相位元件的阻抗ZCPE可表示为:

燃料电池等效电路的整体阻抗可表示为:

式(7)给出的燃料电池阻抗模型具有较强的物理意义,结构简单,可作为燃料电池故障诊断的参考模型。

3 基于FCM聚类和BO算法的PEMFC故障诊断

3.1 PEMFC故障分析

燃料电池发生水淹故障,会阻碍气体充分反应;发生膜干故障,会影响质子传导率,降低电堆输出性能。防止水淹和膜干等不健康状态的发生,对提高电堆输出性能很重要。

从图3可知,PEMFC在正常状态下的总阻抗较小,当处于水淹和膜干状态时,总阻抗均呈现一定程度的增大,膜干时的阻抗谱整体向实轴正方向移动。

图3 PEMFC在不同状态下的EISFig.3 EIS of proton exchange membrane fuel cell(PEMFC)in different states

不同状态下PEMFC的EIS,呈现出明显不同的特征,由此可建立PEMFC故障分类模型。燃料电池阻抗是频率的非线性函数,基于实验数据求解阻抗模型的各元件参数,常用非线性最小二乘法来实现。根据图2所述的带有CPE的燃料电池阻抗模型可知,燃料电池内阻可表示为:

式(8)中:Z′i是阻抗实部;Z″i是阻抗虚部。式(8) 的实部和虚部,分别对应图3的实轴和虚轴,二者均是频率和各元件参数的非线性函数。

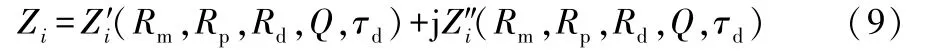
利用泰勒定理展开式(9),计算阻抗模型各元件参数的最佳估计值。燃料电池含水量发生变化时,Q、τd两个参数变化不明显,不适合作为故障诊断的特征向量。选取Rm、Rp和Rd等3个变化明显的参数,作为故障诊断的特征向量。

3.2 PEMFC故障诊断过程

在选择图2阻抗模型的基础上,使用Zview软件对文献[6]得到的阻抗谱进行拟合,得到各阻抗数据。

将文献[6]获取的数据集送入FCM聚类算法,将聚类后的数据拆分为训练集和测试集,训练样本送入BO算法模型中进行学习,最后测试故障样本集,计算分类准确率。

3.2.1 FCM聚类算法

FCM聚类算法通过优化目标函数,使得相似度最高的样本集合成一个簇[7],簇心用Ci表示。实验采集3类阻抗数据,簇心为3。数据集为x=(x1,x2,…,xN),样本xj(j=1,2,…,N)到聚类中心Ci(i=1、2、3)的隶属程度,可以用uij表示,每一个样本数据的uij构成一个隶属度矩阵U。

利用目标函数J对样本非相似度指标进行最小化迭代运算,J及约束条件可表示为:

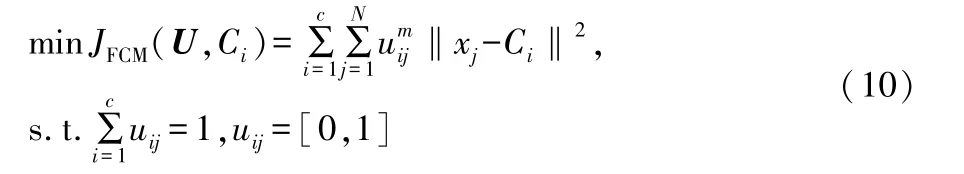
式(10)中:c是聚类个数,为3;N是样本个数;m是模糊化程度,为2。隶属度最小变化量(收敛精度)设置为1×10-6,迭代上限设为100次,当满足迭代终止条件时,聚类结束。

为提高准确度,在使用BO算法进行故障分类前,在MATLAB中构建FCM聚类算法模型,对原始数据进行聚类分析,剔除隶属度不足的样本点。PEMFC阻抗数据在FCM聚类算法中的隶属度矩阵值见图4。

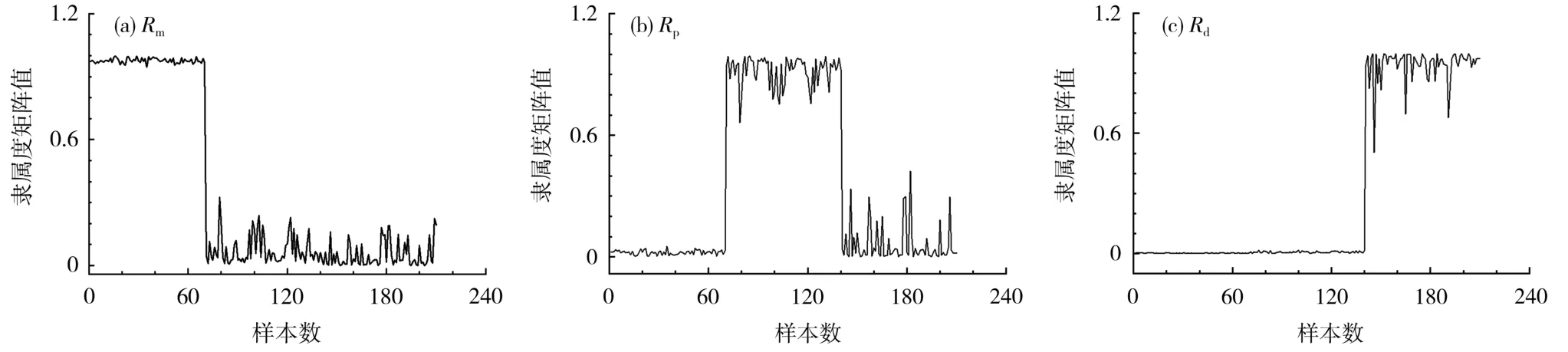
图4 PEMFC阻抗数据在FCM聚类算法中的隶属度矩阵值Fig.4 Membership matrix value of PEMFC impedance data in fuzzy C-means(FCM)clustering algorithm

从图4可知,PEMFC的3类阻抗数据在FCM聚类算法中的隶属度矩阵值中有明显的区分度。样本数据共210组,前70组样本数据为Rm,隶属度矩阵值接近1,构成一个簇。同理,Rp和Rd分别构成一个簇。各簇中剔除隶属度远小于1的样本点,使得后续对样本数据的分类更精确。

FCM聚类算法的迭代次数及目标函数变化值见图5。

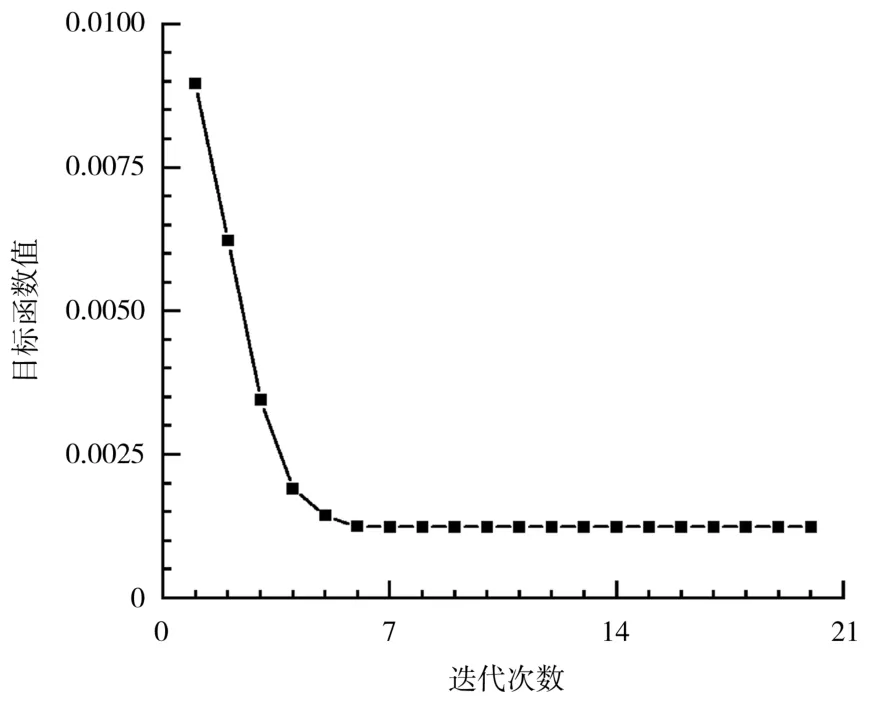
图5 FCM聚类算法的迭代次数及目标函数变化值Fig.5 The iteration times of FCM clustering algorithm and the change value of goal function

从图5可知,FCM聚类算法迭代了7次左右,目标函数开始收敛,即可认为达到局部最优状态。

3.2.2 BO算法分类

经典贝叶斯算法适用于离散型变量,由于阻抗数据属于连续型变量,采用BO算法进行分类。使用训练数据估计分布参数,BO算法通常采用高斯分布作为概率代理模型来表示连续数据的类条件概率分布。高斯过程需计算出样本数据的两个参数,即均值μ和方差σ2,对每个类yi,计算出属性xi的类条件概率作为后验概率,结果即为对应的所属类别。类条件概率的计算如式(11)所示:

式(11)中:Xi是属性类别;Yi是待分类类别;e是自然常数。

获取各类别中各属性的均值、方差后,计算各阻抗数据的所属类的概率,数据集为x=(x1,x2,…,xN),第i个样本有M个属性特征,对于该样本所属类的概率,用该样本所有属性特征概率乘积来表示,即:

对于单个样本返回预测结果,比较所有类别下该样本的概率,找到最大概率值所属类别,即认定该样本属于该类别。

经FCM聚类后,共200组样本数据,按3∶7的比例拆分为训练集和测试集,将训练样本送入上述BO分类模型训练。训练集、测试集应用BO算法分类的结果见图6,其中,分类类别1、2、3分别代表燃料电池正常、膜干和水淹等3种状态。

图6 训练集和测试集应用BO算法分类结果Fig.6 Classification results of training set and test set using Bayesian optimization(BO)algorithm

从图6(a)可知,有2组样本数据预测值与实际值不符,训练集判别结果准确率为96.67%。测试集共140组样本数据,从图6(b)可知,通过计算,BO模型对燃料电池3种状态的判别结果准确率为97.86%。

3.2.3 对比分析

为验证此算法的诊断效果,分别采用支持向量机(SVM)算法和最邻近分类(KNN)算法[8]这两种传统机器学习方法进行对比。SVM算法是一种最大化分类间隔的分类器;KNN算法计算测试样本点到其他每个样本点的欧氏距离,输出该样本点所对应的类别。

使用SVM和KNN算法对该数据样本进行分类,分类准确率分别为89.64%和92.56%,基于FCM聚类与BO算法的分类方法对于燃料电池故障的分类准确率为97.86%,高于传统SVM和KNN算法,且该算法的计算复杂度较低、速度较快,为燃料电池故障诊断提供了一种思路。

4 结论

本文作者通过分析PEMFC内部湿度正常、膜干和水淹等3种不同状态下的阻抗数据特征,选用含CPE的Randles等效电路模型,选取等效电路中具有代表性的3个阻抗参数作为故障特征向量,采用FCM聚类算法对样本数据进行聚类剔除,并采用BO算法对其进行故障分类,得出以下结论:

采用FCM聚类算法对样本特征向量进行聚类,可以剔除隶属度不足的样本点,提高分类的准确率。采用高斯过程作为概率代理模型的BO模型,具有较好的参数寻优结果及诊断性能。

基于FCM聚类和BO的分类算法模型,能对多维数据进行处理,可对多种故障情况做快速准确分类。实例分析结果表明,该方法可快速地辨别PEMFC的正常、膜干和水淹状态,分类准确率达97.86%。与传统单一分类算法相比,该方法具有更高的故障分类准确率。