政府补贴、创新投入与制造业企业全要素生产率

路春城 王翠翠 姜常梅

(1.山东财经大学财政税务学院，山东 济南 250014；2.山东省科学技术情报研究院，山东 济南 250101)

一、引言

制造业的创新能力是国家竞争能力和综合国力的重要体现。当前我国制造业发展面临着低端制造供给替代、高端制造回流发达国家、国内消费需求结构升级、全球生态环境恶化等诸多压力，推动制造业高质量发展是我国经济高质量发展的关键所在，也是加快社会主义现代化建设的重要基石。一方面，企业需加快转变发展方式，提升创新效率和质量，增强自主创新能力，加大创新要素投入，摆脱过去所依赖的高投入、高消耗、高污染的发展模式，实现由追求数量、规模扩张向质量、效率提升转变。另一方面，企业创新活动的外部性以及市场机制的内在缺陷，一定程度上会降低企业进行研发活动的积极性，因此需要加强政府自身建设，全面提高政府效能，建设有为政府，弥补市场失灵。政府补贴作为一项直接给予企业资金支持的政策，对企业全要素生产率提升有直接影响。政府补贴以激发企业创新潜力、促进经济可持续发展为目标，并在维护社会稳定、引导经济发展等方面发挥积极作用。然而，伴随着经济的快速发展和市场体制的不断完善，政府补贴在发挥激励作用的过程中，挤出效应也随之显现。政府补贴对制造业企业的生产效率将产生怎样的差异化影响以及政府是否能够通过补贴有效促进企业的创新投入等这些问题都值得我们进行进一步的研究。

二、文献综述与研究假设

(一)政府补贴与制造业企业创新投入

企业创新活动过程中具有资金投入量大、风险高、收益不确定等特性，这也是导致我国多数企业研发活动不稳定的重要因素。这时需要政府通过政策手段介入以扶持企业发展，其中最为常见的便是政府补贴。一方面通过直接给予企业资金补偿，弱化企业面临的投资收益风险和研发过程中的不确定性，一定程度上弥补了外部性所导致的私人收益与社会收益之间的差距，这对于制造业企业的发展尤其重要，但我国政府补贴方法和效率还有待改善(尚洪涛，2019)[1]。另一方面，政府补贴具有强烈的导向性，通过补贴向外界传递出企业发展前景良好的积极信号，优化外源融资环境，丰富企业创新资源，促使企业研发活动顺利进行(Zcelik和Taymaz,2008[2]；李瑞茜、向俊红，2013[3])，为实现持续发展，企业愈加重视研发创新，加大创新投入力度。而政府在选择受资助企业时往往具有偏好性(白俊红，2011)[4]，并非所有企业都可以获得资助，企业规模、产权类型以及所处地区等的不同使得政府补贴对创新投入的影响呈现差异性。卫舒羽和肖鹏(2021)[5]研究发现，政府补贴对企业研发投入的激励效用随企业规模扩大而增强，财政补贴对国有企业的创新激励作用要大于民营企业。邓超等(2019)[6]从行业、研发强度、地区纬度等方面出发，研究发现政府补贴对中小创新型企业经营绩效的影响存在明显的异质性。刘明广(2019)[7]研究发现政府科技资助对企业创新投入的影响因企业规模和产权类型等不同存在差异性。

在企业进行创新活动过程中需投入大量的人力和物力资源，张志昌和任淮秀(2020)[8]以制造业上市公司为研究样本，实证检验发现政府补贴显著提升了企业创新的人力资本投入水平。储德银等(2016)[9]从研发经费投入和人员资本投入两个角度衡量企业创新投入指标，基于上市公司微观数据实证检验发现，财政补贴对战略性新兴企业创新投入具有显著的正向影响，但对企业研发费用投入的激励效果要优于人力资本投入。基于以上分析，提出假设H1。

H1: 政府补贴能显著促进制造业企业增加研发费用和研发人员投入。

(二)政府补贴与制造业企业全要素生产率

由于变量测算方法、观测样本选取以及实证分析方法上的差异，学术界关于政府补贴对全要素生产率的影响效应仍存在分歧。

有学者认为财政补贴对企业全要素生产率产生正向激励效应，对企业分组实证发现其作用效果具有差异性。企业研发活动中所面临的不确定性以及市场机制调节的内在缺陷等因素，要求政府对特定类型的企业予以补贴，政府补贴会对企业研发支出产生“挤入效应”(Wieser，2005[10]；Sissoko，2013[11])，即政府研发补贴会激励企业加大研发投入，对企业研发具有一定的激励作用，能够促进企业加大研发支出，进而推动企业生产效率提升。由于企业研发活动本身具有不确定性、收益跨期长等特性(任曙明、吕镯，2014)[12]，受到严重的融资约束，相对企业内部融资来说，企业获取外部融资所付出的代价较高(邓可斌、曾海舰，2014)[13]，而在市场环境中，当企业面临融资约束时，资金支持远不能满足企业快速平稳增长所需的实际资金需求，从而抑制企业生产效率的提升，而基于装备制造业数据实证发现，平均而言，政府补贴能完全抵消融资约束对生产率的负面效应，促进企业全要素生产率平稳持续增长，因此财政政策是保持生产率逐年平稳攀升的重要因素。任海云和聂影春(2018)[14]指出政府补助与研发投入有利于企业绩效的提升,但异质性分析发现在东北地区与西部地区企业中作用并不明显,从资源配置效率的角度来看，国有企业获得了远远超过其效率对应的应该获得的资源(杨汝岱，2015)[15]，政府补助对其业绩也无帮助。Bernini和Peuegrini(2011)[16]、武咸云等(2017)[17]研究发现，政府补贴对企业的实际激励效应具有滞后性。

也有学者认为政府补贴对企业全要素生产率有着负向影响。Bardhan(1997)[18]、杨德明等(2017)[19]指出寻租和腐败行为会直接弱化政府补贴实际效果，破坏市场平等竞争机制，严重损害企业经营绩效。蔡栋梁(2018)[20]以沪深主板民营公司数据为样本，研究发现民营上市企业为获取更多补贴通过寻租建立政企关系。但寻租削弱了企业进行研发投入活动的积极性。特别是在腐败严重地区的寻租活动，其负面效应弱化了政府补贴的实际效果。政策制定者与企业之间存在信息不对称(陈文俊等，2020)[21]，在申请政府补贴时，企业往往会有意隐瞒重要信息和传递虚假信息，造成政府补贴资源错配(李政等，2018)[22]，不透明的补贴过程也会抑制补贴实际效果，使得政府补贴的无效率，甚至负效率(徐保昌、谢建国，2015)[23]。李政等(2019)[24]从所有权角度考察发现，相对于国有企业，政府补贴对非国有企业生产效率的提升作用更显著。基于以上分析，提出假设H2。

H2a:政府补贴对制造业企业全要素生产率具有显著正向影响。

H2b:政府补贴对制造业企业全要素生产率具有显著负向影响。

(三)政府补贴、创新投入与制造业企业全要素生产率的作用机理

企业创新投入在政府补贴与制造业企业全要素生产率的研究中是不可忽视的关键因素。从中介效应的传递路径来看，一是企业创新投入与政府补贴的关系。企业研发成果的外部性会降低企业开展创新活动的积极性，政府补贴在一定程度上可以消除其后顾之忧，促进企业创新，同时政府对企业进行补贴具有政策导向性，向外界传递企业发展前景良好的积极信号，丰富企业创新资源，一定程度上还可以改善企业的外界融资约束环境，最大限度激发企业创新投入积极性，促进企业经营绩效的提升。二是企业创新投入与企业全要素生产率的关系。根据熊彼得的创新理论，创新是建立一种新的生产函数，在生产过程中内生化，是经济可持续发展的根本需求。创新投入作为企业技术创新的支撑点，有助于企业不断开发新技术、新产品，形成核心竞争力，从而使企业在激烈的市场竞争中找到自身立足点，促进经济持续健康发展。创新投入通过增加人力和资金投入，可以提高企业的知识存量(Griliches,1986)[25]，改善企业创新要素的投入占比。创新投入对企业全要素生产率的贡献还体现在资源配置效率的改善上，在宏观层面上，资源从效率低的生产部门转移到效率高的部门，在微观层面上，同样体现为劳动和资本等要素在企业的不同生产部门之间流转，直至要素配置水平达到最优，从而进一步提高企业的全要素生产率(邵敏、包群，2012)[26]。王薇和艾华(2018)[27]以2010-2016年我国603家创业板上市公司为研究对象，发现研发资金投入在政府补助与全要素生产率之间存在部分中介效应，且对于不同行业中介效应也存在差异。也有部分学者从研发资金和研发人员两个角度来衡量企业研发创新投入，燕洪国和潘翠英(2022)[28]从研发资金与研发人员两个角度测算创新要素投入指标，研究发现二者在税收优惠对企业生产效率作用的过程中存在中介作用，即税收优惠是通过促进企业加大创新要素投入对企业全要素生产率发挥政策激励作用。然而政府补贴能否通过研发人员投入进一步影响全要素生产率，还需进一步检验。因此，本文认为“政府补贴—创新投入(资金要素投入、研发人员投入)—制造业企业全要素生产率”是政府补贴影响制造业企业全要素生产率的传导路径。基于此，提出假设H3。

H3：企业创新投入在政府补贴对制造业企业全要素生产率的作用过程中发挥了中介效应。

三、模型设定与变量选取

(一)数据来源

本文选取2011-2020年A股制造业上市公司，进行如下筛选操作：(1)剔除*ST、ST类上市公司；(2)剔除存在大量缺失值的公司；(3)为避免极端值的影响，对主要变量在1%和99%的水平上进行缩尾处理。经过上述筛选，最终获取中国制造业上市公司2011-2020年共7906个有效观测值。论文数据取自CSMAR 数据库。本文使用Stata.16软件。

(二)模型设定

政府补贴会通过企业创新投入影响制造业企业全要素生产率，为识别这一机制是否存在，本文借鉴温忠麟和叶宝娟(2014)[29]的方法构建两个模型：基准模型和中介效应检验模型。

1.基准模型

在控制企业年龄(Age)、企业规模(Size)、企业所有权性质(Soe)、企业盈利水平(Roa)、资产负债率水平(Lev)等因素的基础上，检验政府补贴与制造业企业全要素生产率的关系，基准回归模型见式(1)。

TFPit=β0+β1Govsubit+βk∑Χit+μi+λt+εit

(1)

其中，下标i表示企业，下标t表示年份，TFPit为被解释变量，采用LP法测算，表示i企业在t时期的全要素生产率取值。Govsub表示政府补贴，Xit是各种控制变量，μi为个体固定效应，用于控制不同企业间影响机制的差异，λt为时间固定效应，主要用来剔除时间趋势项对回归结果的影响，εit为随机干扰项，主要指模型中未包含的解释变量以及其他因素对被解释变量产生影响的总集合。

2.中介效应模型

在基准回归的基础上，进一步检验政府补贴是否会通过企业创新投入对制造业企业全要素生产率产生影响，创新投入分别从研发资金投入(RDM)和研发人员投入(RDP)两个方面来考量。为此，建立如下递归方程：

RDM=β0+β1Govsubit+βk∑Xit+μi+λt+εit

(2)

TFPit=β0+β1Govsubit+β2RDMit+βk∑Xit+μi+λt+εit

(3)

RDP=β0+β1Govsubit+βk∑Xit+μi+λt+εit

(4)

TFPit=β0+β1Govsubit+β2RDPit+βk∑Xit+μi+λt+εit

(5)

式(2)-(5)中，i、t、μi、λt、εit含义与式(1)相同，β为系数，RDM、RDP为中介变量，分别表示企业研发资金投入和研发人员投入情况。

(三)变量选择与指标测算

1.被解释变量(企业全要素生产率TFP)

现有研究大多采用OP法和LP法测算企业TFP，OP法以投资为代理变量，要求企业投资必须大于0，这一限制造成企业样本损失过多。而LP法以中间投入品为代理变量，通过替换变量的方式有效减少样本损失，相较于OP法更精确。本文使用LP法估计企业TFP。

lnYit=α0t+α1tlnLit+α2tlnKit+α3tlnMit+εit

(6)

上式中，Y是主营业务收入,用营业收入减其他营业收入衡量; L为劳动投入，用员工人数衡量(个) ; K为资本投入，用固定资产净额衡量; M是中间投入，用购买商品、接受劳务支付的现金衡量。下标i为公司，t为年份，在取对数前对上述变量都加1。为剔除样本数据中极端值对实证结果的影响，对 TFP指标在1%和99%的位置进行缩尾处理。

2.解释变量(政府补贴)

本文解释变量为政府补助(Govsub)，用政府补贴强度来衡量，选用CSMAR 数据库中披露的企业年度获得的政府补助数据，并用企业获得财政补助占该年全部营业收入的比重来测算政府补贴强度。通常来讲，政府补贴一方面可以弥补企业研发成果的外部性，缓解企业面临的外界融资约束困境，激励企业进行生产和研发活动的积极性，促进生产效率的提高; 而另一方面，在信息不对称等情况下，财政补贴容易造成企业过度重视规模扩张，忽略研发投入，从而抑制生产效率的提升。因此，政府补贴对制造业企业生产率的影响具有不确定性。

3.中介变量(创新投入)

创新投入不仅包括资金要素投入还包括人员要素投入，本文选用研发资金投入(RDM)和研发人员投入(RDP)衡量我国制造类企业创新投入水平。本文采用研发投入占总资产的比重来衡量研发资金入，采用研发人员数量占企业员工总数比重来衡量研发人员投入。

4.控制变量

为了更准确地研究政府补贴与研发投入对企业TFP的影响，本文将企业年龄(Age)、企业规模(Size)、企业所有权性质(Soe)、企业盈利能力(Roa)、资产负债率(Lev)作为控制变量。考虑到不同产权性质的企业面临的政策环境不同，加入国有企业虚拟变量，政策环境的差异性可能给企业的经营决策带来影响，进而影响企业生产经营效益，和民营企业和外资企业相比，国有企业具有经营规模庞大、人员冗余和组织结构僵化等特征，这可能是导致其生产效率低下的重要因素，所以预期Soe的系数符号为负。

企业年龄(Age)。年轻公司和成熟公司对于市场前景的判断存在差异，这也会影响企业进行研发和创新积极性。企业年龄对其生产率的影响具有不确定性。一方面，成熟企业拥有较多的生产经验，可以提高企业整体的运营效率；另一方面，也可能存在经营模式落后、组织结构僵化的问题。本文以观测年份减去上市年份加1来表示企业的年龄。

企业规模(Size)。相对于规模较小的企业，规模大的企业在规模经济、风险分担和资金来源等方面具有相对优势，因此其具有更强的创新能力。同时，大量的经验研究结论也证实了企业规模对于企业生产率的影响。本文以企业总资产的对数表示企业规模。

企业所有权性质(Soe)。考虑到企业所有权性质不同带来其在研发策略和生产效率上的差异性，加入该虚拟变量，国有为1，非国有为0。

企业盈利能力(Roa)和资产负债率(Lev)。这两个指标可以一定程度上反映企业面临的融资约束，在资金不足时，企业往往会放弃有利的投资机会，导致资源配置扭曲和生产效率低下，即融资约束困境会抑制制造业企业的固定资产投资和创新活动的积极性，进而降低生产率水平。以企业利润总额与营业总收入之比来衡量企业盈利能力，以总负债/总资产来衡量企业资产负债率。变量含义如表1所示。

表1 变量含义和计算方法

(四)变量描述性统计

表2显示，制造业企业全要素生产率均值为 3.47，最小值为2.78，最大值为 4.62，标准差为 0.33，说明所选样本的全要素生产率明显偏低。政府补贴均值为0.650,且从标准差0.65、最大值 3.480 与最小值 0.010 可以看出,政府对制造业上市企业的补助存在差距大、分布不均的现状。此外，由表2可知，2011-2020年A股上市公司RDM的均值为2.630，表明我国企业资金投入水平整体偏低，且标准差为1.790、最大值为9.970与最小值为0.060，另外企业研发人员投入最大值与最小值相差很多，不同企业之间研发资金投入与研发人员投入水平差距很大，这也表明现阶段从整体上提高我国企业创新投入积极性的紧迫性与必要性。

表2 描述性统计

四、实证检验与结果分析

(一)相关性分析

由表3可知，政府补助( Govsub)、企业研发资金投入(RDM)、研发人员投入(RDP)与制造业企业全要素生产率(TFP)之间均在1%水平上呈现出显著正相关，政府补助(Govsub)与企业研发资金投入(RDM)、研发人员投入(RDP)之间也在1%水平上显著相关。为明晰变量间更为细致的关系、得出真实可靠的研究结论则需要通过多元回归分析展开进一步研究。表3显示各解释变量之间的相关系数最大为0.533，均不超过0.6，结合各变量的方差膨胀因子(VIF)值远低于阈值10，表明本文研究变量之间不存在多重共线性问题，可进一步进行回归分析。

表3 各变量间的相关系数

(二)基准回归

表4为政府补贴对制造业企业全要素生产率的影响以及企业创新投入的中介效应检验回归分析结果。由表4可以看到，无论是否加入控制变量，政府补贴的系数都在5%的水平上显著为正，这表明对于制造业企业来说，政府补贴力度越大，企业的生产力越高，即政府补贴对制造业企业TFP产生一定的促进作用，验证了本文假说H2a。随着企业规模扩大、年龄增长以及盈利水平的提升，企业自身的全要素生产率也会显著提高，而随着资产负债率提高，全要素生产率会显著下降。列(3)为政府补贴对企业研发资金投入的影响效应,回归结果显示政府补助(Govsub)与研发资金投入(RDM)的回归系数为0.156，在1%水平上显著正相关，H1得到支持；列(5)为政府补贴对企业研发人员投入(RDP)的影响效应,回归系数为0.239，政府补贴显著促进制造业企业重视人才吸引，H1得到支持；列(4)在列(2)的基础上加入了中介变量企业研发资金投入(RDM)，检验发现政府补贴对制造业企业TFP的回归系数由原来的0.004上升到0.013，且在5%的水平上显著；列(6)在列(2)的基础上加入了中介变量企业研发人员投入(RDP)，政府补贴与制造业企业TFP仍具有显著正相关性，研发资金投入与研发人员投入在政府补贴与企业全要素生产率之间发挥部分中介作用，H3得到支持。

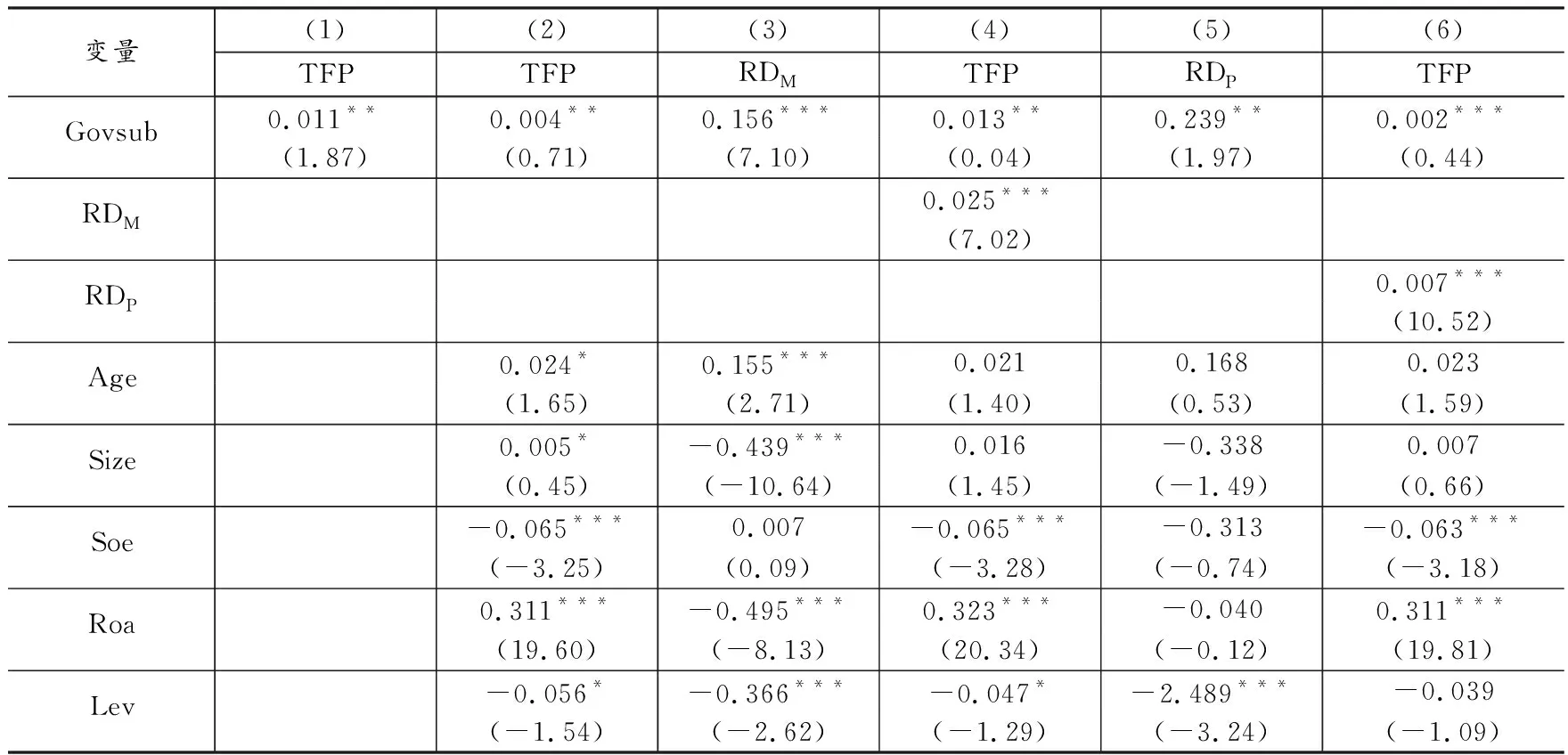
表4 政府补贴对制造业企业全要素生产力的影响——企业研发投入的中介效应检验

续表4

(三)稳健型检验

1.考虑内生性问题的检验

为尽可能克服内生性问题，本文运用工具变量法，将政府补贴滞后1期作为工具变量，选用两阶段最小二乘法( 2SLS)进行估计。结果如表5列(1)所示，政府补贴显著促进企业TFP的提高，与前述估计结果一致。

2.变换全要素生产率测算方式

采用OP法计算企业TFP，观察政府补贴对制造业企业TFP的影响，如表5列(2)所示，政府补贴(Govsub)的系数和显著性无明显变化，表明研究结论是稳健的。

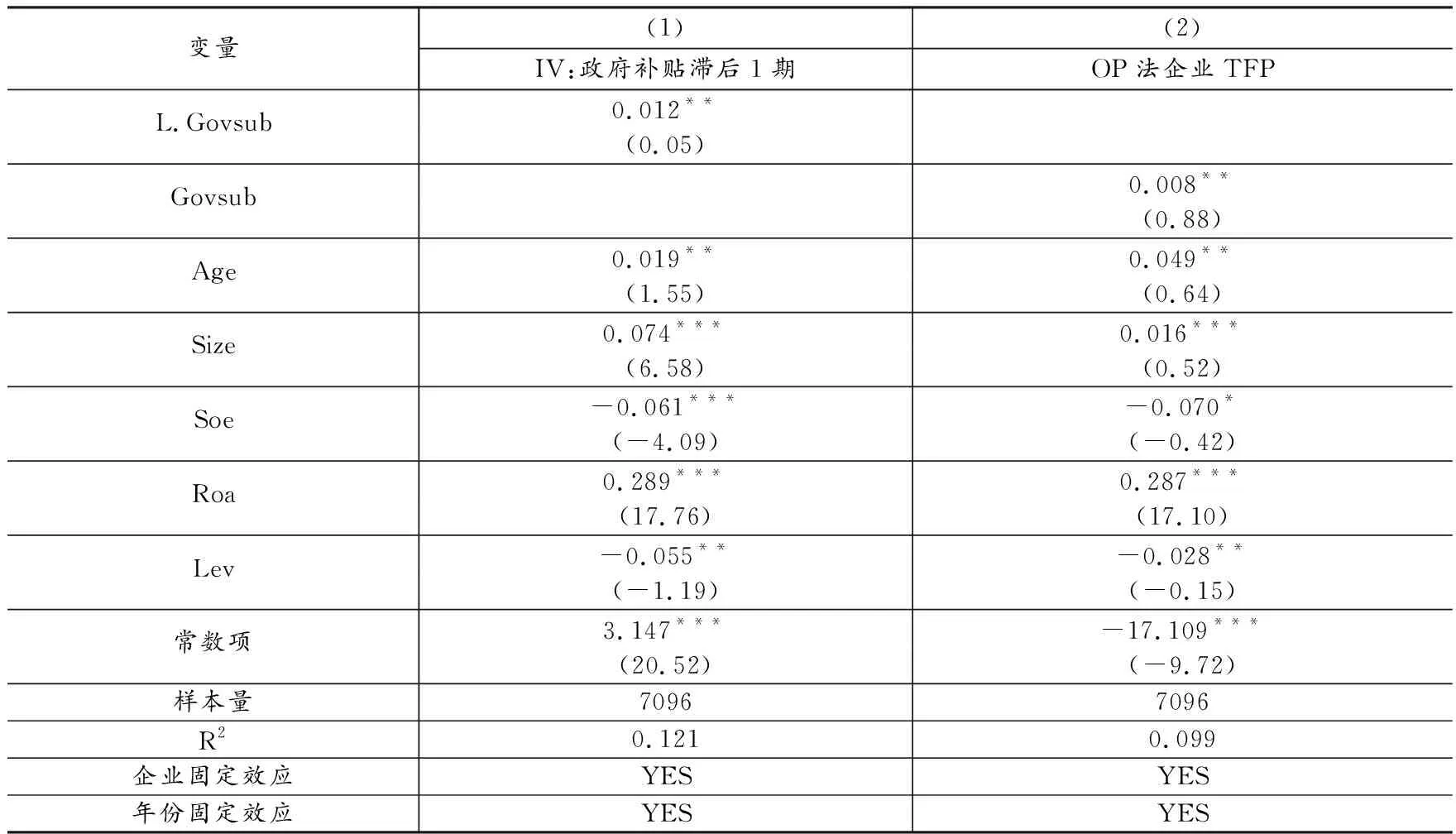
表5 稳健性检验

(四)异质性分析

1.考虑企业所有制不同

为了获得更为直观的结果，依据所有权性质本文将制造业企业分为国有企业和非国有企业进行分样本回归，如表6 PartA所示，就国有企业而言，政府补贴显著抑制了全要素生产率的提升; 而对非国有企业，政府补贴虽然提升了全要素生产率，但效果并不显著。国有企业相对于非国有虽然具有政策优势，更容易获得政府资金支持，很少会有资金短缺的紧张感，并掌握研发资金、科技人才等大量创新资源，但对财政资金的依赖性很低，在补贴资金的使用效率上不如依赖性高的非国有企业，存在补贴资金利用低效率问题。

2.考虑企业生命周期不同

本文将研究样本按照企业年龄分成3组，即初创期(Age<15)、成长期(15≤Age<20) 和成熟期(Age≥20)，分样本回归结果见表6 PartB，政府补贴对处于成长期的制造业企业TFP的影响最为显著(在5%的显著性水平下为正，且系数为0.406)，对初创期和成熟期制造业企业TFP影响效应不显著。究其原因，初创期企业处于产品开发阶段，面临融资约束压力，政府补贴可以帮助初创期企业在一定程度上克服资金约束，激励企业加大研发投入，促进生产力提升；进入成长期阶段，企业有一定的知名度，企业创新意识较强，但仍面临融资约束，政府补贴具有一定政策导向性，促使其加大创新要素投入，生产效率提升显著；进入成熟期，企业拥有了自己的主导品牌，内部人员组织结构复杂，一项投资决策往往需要多方共同决定，品牌具有知名度，占有较高的市场份额，销售收入多元化且稳定，而政府补贴在自身收入中占比不高，不能对全要素生产率造成显著影响。

表6 不同样本下政府补贴影响制造业企业全要素生产率的差异分析

3.考虑企业所处区域不同

本文根据我国地区划分将制造业企业样本划分为东、中、西部三个组内，并分组进行回归分析。具体结果如表6 PartC所示，在中部地区与西部地区，政府补贴有效促进当地制造业企业全要素生产率提升，而在东部地区，政府补贴对企业TFP积极效应并不显著。可能是因为在获得政府补贴后，由于各地区发展水平和环境等方面的差异性，东部地区发展水平高、产业规模较大，对政府的依赖程度较小，政府补贴对该地区企业效益的提升有限。而中部和西部地区无论是发展水平还是在获取信息上多不如东部地区的企业，自身生存压力大、发展需求强烈，导致两地区的企业往往对政府补贴有着更强的依赖性，政府补贴对两地区制造业企业促进作用显著。

4.考虑要素密集度

要素密集度反映了企业在生产过程中对于劳动、资本和技术等生产要素进行选择的状况，随着我国人口红利的逐渐消失，依赖劳动力优势的制造业也进入发展瓶颈。根据要素密集度分组，研究分析政府补贴对制造业企业全要素生产率的差异性具有重要意义，根据制造业要素结构将制造业划分为劳动、资本以及技术密集型三组并进行分样本回归。

由表7可以看出，政府补贴对三类要素密集型企业全要素生产率的影响存在显著差异性，列(1)Govsub的估计系数为-2.087，表明政府补贴对劳动密集型制造业TFP具有显著的抑制效应；列(2)Govsub的估计系数为0.509，虽不明显但正系数反映了政府补贴与资本密集型制造业TFP存在一定的正向关系；列(3)表明政府补贴能显著促进技术密集型制造业企业TFP的提升。这可能是因为要素密集度反映了企业的要素选择状况。劳动密集型产业以中小企业为主，在人才、资金储备上不占优势，在发展中更倾向于将政府补贴投入到规模扩张中，技术密集型产业投资量大、资金周转较快、面临的融资约束较大，政府补贴积极效应更显著。

表7 行业异质性检验结果

五、研究结论与政策启示

(一)研究结论

本文采用2011-2020年中国制造业上市公司数据，考察政府补贴对企业全要素生产率的影响和作用机制，并探讨了这种影响的异质性。研究发现，第一，政府补贴会显著促进制造业企业全要素生产率提升，通过采用两阶段最小二乘法消除变量内生性以及变换生产率测算方式进行稳健性检验，这一结论保持不变。第二，企业创新投入在政府补贴与企业全要素生产率之间存在中介效应，即政府补贴通过激励企业加大资金投入和研发人员投入，促进制造业企业全要素生产率的提升。第三，政府补贴对不同类型制造业企业的全要素生产率的影响差异显著。从所有者性质来看，政府补贴对国有企业表现出强烈的抑制影响；从企业生命周期来看，政府补贴对成长期企业全要素生产率促进作用最显著，成熟期次之，初创期最小；从地区分布来看，政府补贴对在中部地区、西部地区的制造业企业全要素生产率有显著促进作用，而对于在东部地区的企业效果不佳；从要素密集度来看，政府补贴对技术密集型制造业积极效应最显著，资本密集型企业次之，对劳动密集型企业具有显著的消极效应。

(二)政策启示

一是重视政府补贴的积极效应，全面落实创新发展战略。在人口红利逐渐消失和资源消耗的压力下，为了给经济可持续发展赋能，政府应当在企业研发创新领域充分发挥政府职能，通过补贴的方式对创新企业给予弥补。

二是充分发挥企业创新投入的中介作用。一方面，充分发挥政府补贴对制造业企业创新投入的杠杆作用，政府选择受补贴企业不能仅仅着眼于弥补私人收益与社会收益间的缺口；另一方面，企业应重视对研发人员创新积极性的激励，完善有效的研发考核机制和合理的奖惩制度，提升员工的归属感，最大效率地将员工创新能力转化为企业实际生产力。

三是充分考虑制造业企业所有制、生命周期以及地区等异质性因素，丰富政府补贴的形式与内容，使政府补贴更具有针对性和精准性。在补贴上应适当侧重于非国有企业和中西部地区的制造业企业，适度加大对重点领域内的初创期、成长期制造业企业的补贴，提高对于成熟期企业获得补贴的技术水平以及成果转化率要求。要促进劳动密集型与资本密集型制造业有机融合，着重发展资本密集型企业，通过具有针对性的补贴政策激励技术密集型企业增加资产投入和创新投入，加速制造业产业结构转型升级。